基于排隊論的除冰飛機延誤分析

陳 斌 張 洋 焦琳青

1(中國民航大學航空地面特種設備研究基地 天津 300300)2(中國民航大學電子信息與自動化學院 天津 300300)

0 引 言

冰雪天氣下為保障飛行安全，離港航班必須要進行除冰作業。除冰作業是影響航班正點率的重要因素，任何除冰作業過程中的干擾都可能加重飛機離港延誤，由此帶來巨大的經濟損失[1-2]。因此，在現有除冰資源配置下對飛機除冰延誤機理進行分析，研究離港動態變化時的除冰航班延誤隊列及指標，可以優化除冰資源的分配，減小除冰資源的消耗，使得冰雪天氣下航班除冰運行效率最大化。

國內外許多學者從多方面對飛機除冰延誤問題進行了研究，并取得豐富的研究成果。在除冰運行控制方面，Mogford等[3]開發了航班意識協作工具，為塔臺、航空公司及除冰作業人員提供決策依據。陳斌等[4]提出一種基于無線數據傳輸的多信息集成飛機地面集中除冰監控系統，大幅提高了飛機地面除冰效率。在除冰飛機調度方面，Fan等[5]提出一種基于數據驅動的除冰活動管理構架，利用隨機動態編程(SDP)方法將除冰飛機分配到各除冰坪，然而，由于大量實際除冰運行數據很難獲得的限制，未獲得推廣應用。Lee等[6]開發了基于排隊論的決策支持工具(DST)，對除冰完成時間進行預測，減少了除冰作業過程中的潛在干擾。沈文興[7]建立了飛機除冰與起飛兩階段串聯的排隊模型，分析了航班安排速率與除冰飛機延誤的關系。在除冰資源分配方面，Zou等[8]建立了整個機場的除冰排隊模型，為除冰車分配提供一種定量分析方法。陳飛[9]建立了多機坪多隊列等待制排隊模型，通過對除冰位進行合理分配以減少除冰延誤。邢志偉、張偉等[10-12]提出了基于博弈論及非合作博弈的除冰資源分配模型，保證了除冰資源分配的公平性，有效緩解了機場離港航班的延誤情況。

上述研究中，文獻[6-9]均采用定常參數的排隊模型，忽略了模型參數隨環境狀態變化這一本質特征，所得結果并不能反映真實情況，文獻[10-12]對考慮航班離港動態的除冰延誤相關機理、延誤參數數值分析缺乏深入研究，對于多除冰坪除冰運行狀況沒有系統的分析。針對以上問題，本文建立了隨機環境下的多除冰坪飛機除冰排隊模型，利用矩陣幾何解方法得到了除冰航班延誤隊列性能指標。以首都機場飛機地面除冰作業為研究案例，獲取不同天氣狀況下除冰飛機到達率，除冰服務率等動態除冰運行數據，并通過仿真模擬驗證模型的有效性和準確性。

1 飛機地面除冰排隊問題分析

1.1 飛機地面除冰流程

飛機地面除冰作業是一個具有高度非線性特性的隨機服務過程，可以借助排隊理論分析飛機地面除冰排隊問題。該問題由兩個過程構成，申請除冰飛機到達指定除冰坪等待除冰作業及除冰坪的除冰機位提供除冰服務。如圖1所示，機場通常具備多個除冰坪，每個除冰坪含有多個除冰機位，除冰飛機與多除冰機位構成一個排隊系統。系統中每架飛機的除冰過程都要經過如下步驟：機組向除冰中心提出除冰申請、除冰中心分配除冰坪、除冰飛機滑行至指定除冰坪排隊等待、除冰作業和除冰完成離去[13-14]。其中，除冰完成的飛機若在防冰液保持時間內沒能及時起飛，該飛機需要再次進入除冰排隊系統等待二次除冰服務。二次除冰會導致稀缺除冰資源的極大浪費，因此，對除冰飛機延誤隊列進行分析，對于除冰資源合理分配，避免二次除冰具有重要意義。

圖1 飛機地面除冰排隊示意圖

1.2 基本假設和前提

鑒于除冰作業過程相關參數的非線性特性，為方便除冰排隊模型的建立、分析和求解做如下合理假設：

1) 冰雪天氣下所有離港航班都需要進行集中除冰雪作業，離港計劃中航班離港率即為除冰排隊模型的到達率，除冰飛機到達的時間間隔相互獨立的并且服從Poisson分布。

2) 各除冰坪均設置一塊除冰等待區域，除冰機位能夠為所有型號飛機提供除冰服務，除冰服務時間間隔服從負指數分布，除冰服務率不隨時間改變。

3) 離港高峰時段所有除冰機位一直被占用，除冰飛機均遵循先到先服務(FCFS)等待制的排隊規則，且不考慮飛機二次除冰問題。

上述特征符合M/M/c模型的假設條件[15]，本文采用該模型分析除冰飛機到達率的動態變化對飛機除冰延誤的影響。同時認為除冰等待區內空間無限，每個除冰坪可以進一步假設為隨機環境下的M/M/c/∞/∞/FCFS排隊模型。

2 除冰飛機到達率及除冰服務率

2.1 除冰飛機到達率

冰雪天氣下航班離港不確定因素增強，因此除冰飛機到達率也是動態變化的，在時間分布上呈現隨機和不均衡性，主要表現在不同時段到達率具有明顯的波動性。圖2為2018年冬季首都國際機場小雪、中雪及大雪天氣除冰飛機到達率的實際數據分布。飛機地面排隊除冰產生的延誤分布主要集中在除冰飛機到達率曲線第一個峰值處，以圖2中05:00-13:00產生的除冰延誤進行分析研究。

圖2 除冰飛機到達率分布

為了更加客觀真實地反映飛機地面除冰的實際運行狀況，引入Markov環境刻畫除冰飛機到達率的動態變化。通常情況下定常參數排隊系統其基本參數是固定不變的，Markov環境下的排隊系統隨著系統的運行其參數本身也在隨機變化[16]。以圖2為例，將05:00-13:00時段每隔1小時劃分為8個時段，每個時段為一個隨機環境。由于除冰飛機到達時間間隔符合Poisson分布的特點，得到具有8個狀態的隨機環境最小生成元矩陣Q為：

由于分配到每塊除冰坪的除冰飛機都是除冰中心以隨機策略從總的離港航班流中分出來的(見圖1)，根據泊松分布的可分解性，以隨機策略分配到每塊除冰坪的飛機到達過程仍服從泊松分布，以λm表示隨機

環境m下機場總的除冰飛機到達率，除冰坪n到達率滿足：

λn=pnλm

(1)

2.2 除冰服務率

除冰服務率與天氣因素、除冰飛機機型等因素有關，確定的天氣狀況下，不同型號飛機的除冰時間各不相同，考慮機型差異以平均服務率表征除冰機位的服務效率，假定機場有ω種機型飛機，各機型比例為：σ1，σ2，…，σω，對應機型的除冰時間為：t1，t2，…，tω單個除冰機位平均服務率可以表示為：

(2)

由于確定天氣狀況及機型比例條件下單個除冰機位的平均服務率是相對穩定的，不受隨機環境狀態的影響，因此，隨機環境狀態下各除冰坪除冰機位的平均服務率均為：

u1=u2=…=uc=u

(3)

將每個除冰機位的平均服務率互相疊加，對于有c個除冰機位的除冰坪，總的除冰服務率為cu，整個機場的除冰服務率可以由各個除冰坪的除冰服務率互相疊加得到。

3 飛機地面除冰排隊模型

3.1 模型構建

根據上面的分析，本文使用二維Markov動態系統中的擬生滅過程(QBD)建立飛機地面除冰排隊模型[17]，以L(t)、J(t)分別表示t時刻除冰排隊系統中飛機數及隨機環境狀態，則QBD過程{(L(t),J(t);t≥0)}的狀態空間為Ω={(k,j);k≥0,1≤j≤m}，把QBD過程的元素按字典順序排列，其生成元矩陣如下：

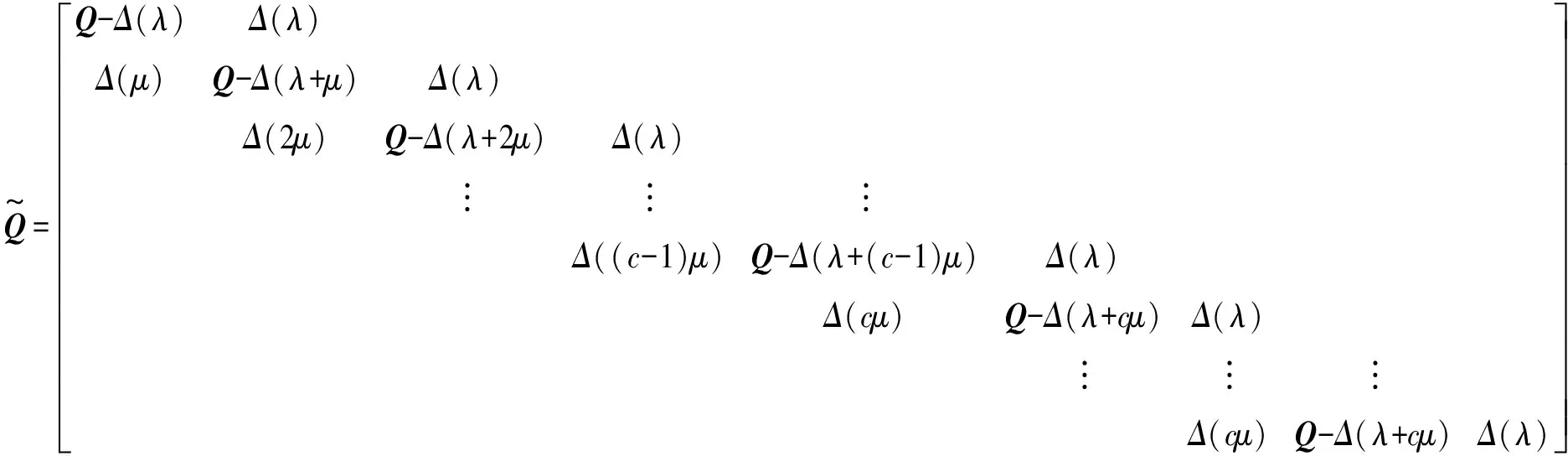
其中:λ=(λ1,λ2,…,λm)T，u=(u1,u2,…,um)T，Δ(λ)=Diag(λ1,λ2,…,λm),Δ(u)=Diag(u1,u2,…,um)。

引入A、B、C三個參數：

A=Q-Δ(λ+cu)B=Δ(λ)C=Δ(cu)

(4)

矩陣塊C、B、A分別表示除冰排隊系統中飛機數增加、減少一個和不變情況下系統狀態變化的描述，且A+B+C=Q，則環境生成元Q的穩態概率向量π滿足：

πQ=0πe=1

(5)

式中:π=(π1,π2,…,πj,…,πm)，其元素πj表示系統處于隨機環境j的概率。若πλ<πu，由矩陣幾何解方法可得QBD過程的穩態分布滿足：

xk=π(I-R)Rkk≥c

(6)

式(6)中率陣R為矩陣方程：R2B+RA+C=0的最小非負解，且sp(R)<1，率陣R可由下列迭代式求出：

R0=0,Rn=(A+Rn2C)(I-B)-1n≥1

(7)

3.2 性能指標

機場除冰作業過程主要關注除冰飛機集散效率及除冰服務水平。其中最能反映除冰飛機集散效率的是除冰飛機平均延誤時間，最能反映除冰服務水平的是除冰飛機延誤架次，而平均隊長可以提供離港高峰時段的平均延誤架次，隨機環境下的條件隊長能夠刻畫各個時段誤架次的動態變化過程。通過對排隊模型分析得到系統的延誤指標如下：

1) 隨機環境j上，延誤架次為k的概率，即條件隊長分布為：

(8)

這里[a]j表示向量a的第j個分量。

2) 隨機環境j上延誤航班架次，即排隊系統條件隊長為：

(9)

3) 離港高峰時段平均隊長，即航班平均延誤架次為：

(10)

4) 離港高峰時段單航班平均延誤時間為：

(11)

將隨機環境狀態與QBD過程生成元矩陣的穩態分布及率陣R代入式(8)-式(11)即可得到除冰排隊系統各項性能指標，為飛機地面除冰延誤分析提供科學依據。

4 模型仿真

根據首都國際機場航空器地面除冰運行手冊，跑道南向北運行時1至4號除冰坪可提供除冰服務，其中3、4號除冰坪除冰機位配置相同，本文利用首都國際機場三種天氣狀況下的實際離港航班數據及除冰資源配置參數，對1至3號除冰坪的運行狀況進行仿真分析。

4.1 仿真參數

將圖2中5:00-13:00每隔1小時劃分為8個隨機環境狀態，得到小雪、中雪、大雪時機場總的除冰飛機到達率λ分別為：

λs=(45,66,69,47,33,40,45,44)T
λm=(42,67,61,43,31,38,47,40)T
λb=(36,59,60,41,33,33,45,50)T

由于1至3號除冰坪分別有3、6、5個除冰機位，則總的除冰飛機到達率分別以概率0.16、0.32、0.26分流到三塊除冰坪。通過對首都機場歷史除冰運行數據和離港航班數據的統計分析，得到C、D、E三類飛機的機型占比及不同天氣狀況下單航班的除冰時間如表1所示，根據表1數據，通過2.2節分析得到三塊除冰坪不同天氣狀況的除冰服務率如表2所示。

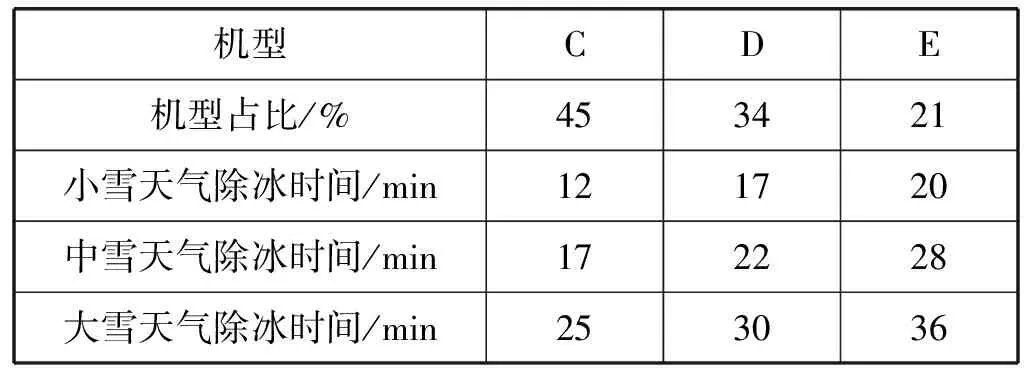
表1 機型占比及各機型不同天氣下除冰時間

表2 除冰坪服務率

4.2 仿真結果及分析

根據除冰排隊模型設計仿真程序，仿真平臺為研華IPC-610，CPU主頻為2.8 GHz，內存為3.24 GB，取迭代誤差精度eps為10-7，設定仿真參數，得到算法運行時間為0.149 s，模型具有較高精度和求解效率，仿真結果分析如下。

4.2.1除冰排隊系統條件隊長分析

由式(8)和式(11)得到小雪、中雪、大雪天氣狀況下，各除冰坪5:00-13:00排隊系統條件隊長的動態變化如圖3至圖5所示。

圖3 小雪天氣1至3號除冰坪航班延誤架次

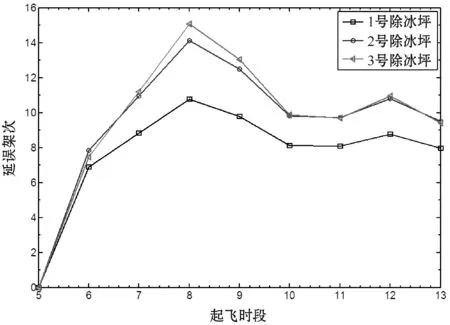
圖4 中雪天氣1至3號除冰坪航班延誤架次

圖5 大雪天氣1至3號除冰坪航班延誤架次

由圖3至圖5可以看出，每個環境狀態除冰飛機的到達率不同，其對應的條件隊長也會發生變化，天氣狀況越惡劣、除冰飛機到達率越高條件隊長越長，延誤航班架次越多。不同天氣狀況下，上午八點的除冰高峰會造成后續除冰過程的持續擁堵；相同天氣狀況時對于除冰機位數多的除冰坪分配到該除冰坪的除冰飛機數越多，由于高峰到達率的沖擊效應，該除冰坪延誤的航班架次也相應增多。

4.2.2除冰飛機平均延誤架次及延誤時間分析

根據上述仿真參數及式(9)和式(10)計算，得到離港高峰時段各除冰坪三種天氣狀況下航班平均延誤架次及平均延誤時間如表3、表4所示。

表3 離港高峰時段航班平均延誤架次

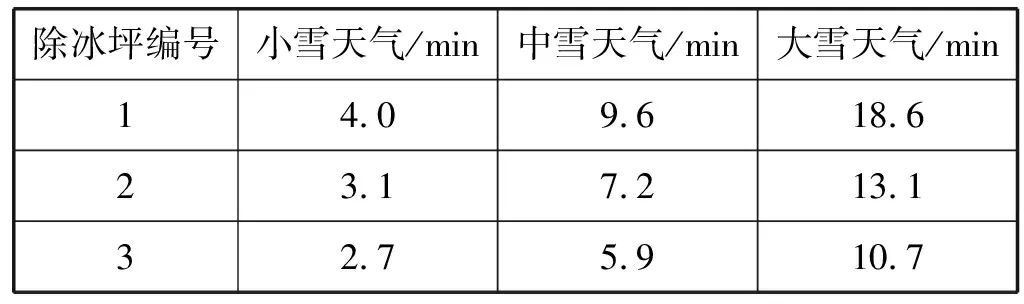
表4 離港高峰時段平均延誤時間

由上述仿真結果可知，天氣狀況越惡劣航班延誤架次越多平均延誤時間越長，為驗證仿真結果的準確性選取1號除冰坪大雪天氣仿真結果為驗證對象。根據文獻[10]中首都機場除冰運行數據，延誤架次及平均延誤時間分別為16.2架與19.6 min,本文仿真結果為16.7架與18.6 min，延誤架次及平均延誤時間誤差分別為0.16%及5.2%，表明本文基于QBD過程的除冰飛機排隊模型，能夠準確描述除冰飛機延誤狀況。

5 結 語

針對確定除冰資源配置條件下，飛機地面除冰延誤問題，本文建立了基于QBD過程的多除冰坪飛機除冰排隊模型，并運用矩陣解析法對模型分析求解，得到如下結論：

1) 利用隨機環境描述除冰飛機到達率的動態變化，將離港高峰時段抽象為有限位相Markov更新過程，采用不可約生成元矩陣刻畫環境狀態的更新轉移。針對除冰服務率的多參數耦合特征，引入平均除冰服務率的多項式描述得到多除冰坪服務效率。

2) 以首都機場1至3號除冰坪為除冰運行實例，根據除冰飛機的到達特征，通過不同參數的取值改變，得出不同天氣狀況，除冰機位數量及除冰飛機到達率下的延誤變化規律，延誤參數仿真結果與實際數據有較高契合度，最大誤差在5.2%以內，說明基于QBD過程的除冰排隊模型可以用于除冰飛機到達率動態變化時的除冰延誤問題研究。

3) 排隊系統除冰飛機到達情況是隨機的，也是動態變化的。以條件隊長描述多除冰坪不同時段除冰飛機延誤架次的起伏變化，通過多除冰坪不同天氣狀況延誤參數的交叉比較定量給出高峰時段到達率對后續排隊的影響，使得除冰決策者能夠在延誤發生前采取措施避免或者補救，為機場除冰運行控制提供理論依據。