結構附設粘滯阻尼器的支撐剛度取值范圍研究

張克誠 王健

(甘肅第五建設集團公司 天水741000)

引言

目前,粘滯阻尼器減震技術已逐漸成熟,在實際工程中得到了廣泛應用。同時,我國最新的《建筑抗震設計規范》(GB50011 -2010)[1]也給出了關于房屋消能減震設計的要點,其中第12.3.5條規定： 速度線性相關型消能器與斜撐、墻體或梁等支撐構件組成消能部件時,支撐構件沿消能器方向的剛度kb應滿足kb≥(6π/T)cd,T 和cd分別為結構的基本自振周期和線性粘滯阻尼器的阻尼系數。實際上,非線性粘滯阻尼器(即α0＜1.0)因其具有更好的耗能性能而在工程應用中更為普遍,但規范尚未給出其適用范圍,致使在采用非線性粘滯阻尼器對結構進行減震設計時只能夠通過多次反復試算來確定,當支撐剛度的取值過小或過大時會導致阻尼器不能被充分利用或工程造價增加。

盡管現有的相關文獻已對非線性粘滯阻尼器支撐剛度的影響進行了深入探討,但仍有待進一步完善。Losanno 等[2]以一個工程案例研究了線性粘滯阻尼器的支撐剛度對結構動力特性的影響,但沒有給出支撐剛度的通用取值范圍。Xu等[3]針對金屬屈服型阻尼器給出了支撐剛度與結構側向剛度之比的大致范圍,但并不具體,難以用于指導實際工程設計。Chen 等[4]研究了支撐剛度對多自由度彈性體系附設線性粘滯阻尼器后的地震響應的影響規律,但并未給出支撐剛度的適用范圍。歐進萍等[5]研究了四類被動耗能器的參數對減震效果的影響,其中給出了僅關于線性粘滯阻尼器(α0=1.0)支撐剛度的取值范圍。從圖1 中可知,當阻尼器的速度小于1m/s 時,非線性粘滯阻尼器(如α0=0.3)的阻尼力明顯大于線性粘滯阻尼器(α0=1.0)的阻尼力,其對應所需的支撐剛度也明顯要大于線性粘滯阻尼器。蔣通等[6]以線彈性SDOF 體系為例,建議了非線性粘滯阻尼器支撐剛度的取值范圍,但前提是需要知道結構在設計地震動作用下的最大位移,導致支撐剛度的取值隨結構最大位移的改變而變化,這與抗規給出的形式有所不同。

圖1 阻尼力與速度的關系Fig.1 Relation between damping force and velocity

綜上所述,可用于指導工程應用的非線性粘滯阻尼器支撐剛度的使用范圍尚需進一步探討。現有的研究結論大多假定結構附設非線性粘滯阻尼器后一直處于彈性狀態,但Symans 等[7]指出,大多數附設粘滯阻尼器的減震結構在強震作用下將會進入不同程度的彈塑性狀態,這可能引起結構基底剪力的顯著增加,因此,結構的非線性影響不可忽略。本文分別建立彈性和彈塑性SDOF體系計算模型,并同時考慮結構和阻尼器的非線性等特性,在文獻[5]的基礎上拓展分析了支撐剛度對非線性粘滯阻尼器結構地震響應的影響規律,并建議了支撐剛度的最小取值范圍,同時保持支撐剛度的形式與規范一致,便于設計人員在進行相關減震結構設計時參考。

1 阻尼器-支撐SDOF體系

粘滯阻尼器減震裝置由阻尼器和支撐兩部分組成,阻尼器一般通過與支撐串聯后布置在結構中,如圖2a 所示。其力學計算模型可以簡化為Maxwell 模型,即由一個阻尼系數為cd的純阻尼器單元和剛度為kb的彈性彈簧單元串聯組成,如圖2b 所示。

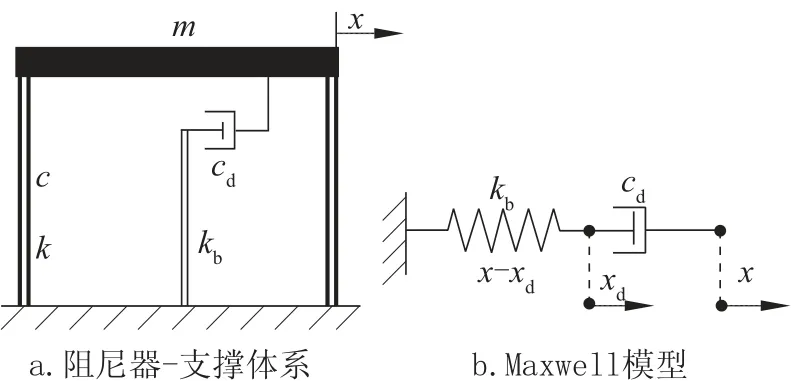
圖2 粘滯阻尼器結構SDOF 體系模型Fig.2 SDOF system model of viscous damper structure

1.1 線彈性體系

當該體系在地震作用下始終處于彈性狀態時,其動力方程可寫為：

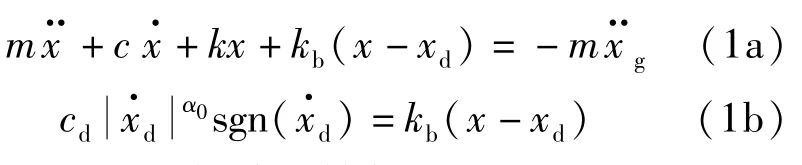
式中： m、 c、 k 分別為結構的質量、 阻尼和剛度; x、、分別為結構相對于地面的位移、 速度和加速度; xd 和分別為粘滯阻尼器的實際行程和速度,為地面加速度; kb、 cd和α0分別為粘滯阻尼器的支撐剛度、 阻尼系數和速度指數(工程應用取值范圍0.3 ～1.0)。

同時, 假定支撐剛度kb和阻尼系數cd分別與結構對應樓層的側向剛度k和阻尼系數c呈線性比例, 并定義無量綱參數α和β分別為：

將式(2)帶入式(1a)后化簡得到式(3)：

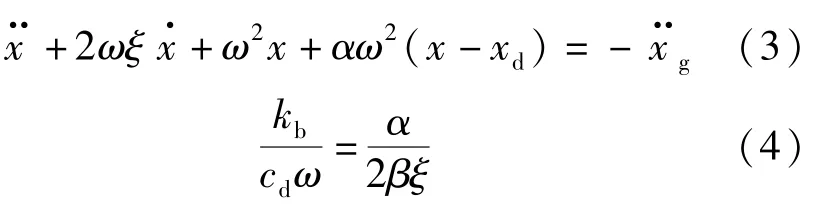
利用數值微分算法求解式(3),即可得到減震結構在彈性狀態下的地震響應。

1.2 彈塑性體系

當該體系在地震作用下進入彈塑性狀態時,其動力方程可寫為：

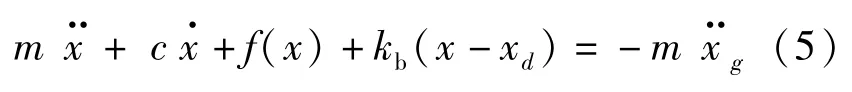
式中：f(x)為彈塑性恢復力,此處采用雙線性強化模型來描述該體系的動力特性,如圖3 所示。圖中α1為結構屈服后剛度與屈服前剛度之比。

同時,定義強度折減系數R和延性系數μ分別為：

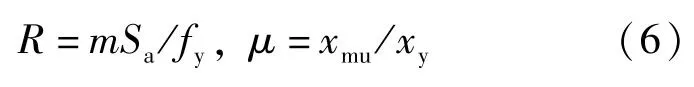
式中：Sa為彈塑性體系對應的彈性體系的加速度反應譜值;fy=kxy為結構的屈服力;xmu為彈塑性體系的最大位移;xy為屈服位移。將式(6)代入式(5)后化簡,得：

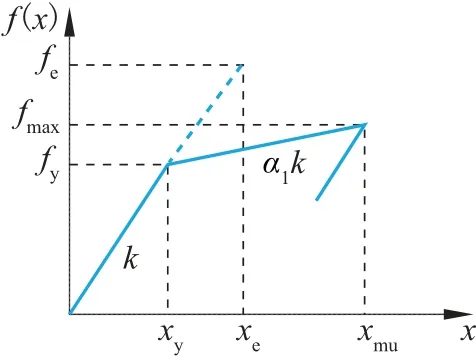
圖3 SDOF 結構Bilinear 強化模型Fig.3 Bilinear harding model for SDOF structure

利用Gear 向后差分法對式(7)進行編程求解,即可得到減震結構的彈塑性地震響應。

2 參數影響分析

現以El Centro 地震波作為輸入,分析各項參數對SDOF 減震體系地震響應的影響。同時,為明確附加阻尼的影響,定義減震結構的附加阻尼比 ξ1為[8]：

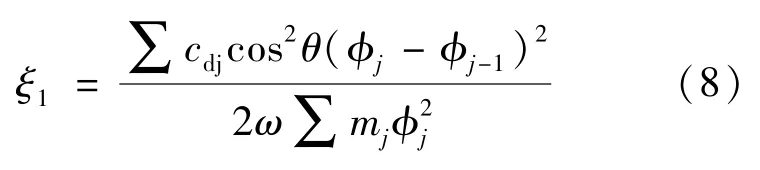
式中： ?j為結構基本振型在第j 樓層的水平位移; mj和cdj分別為第j 樓層的質量和阻尼器的阻尼系數; θ 為阻尼器與樓層水平方向的夾角; ω為結構的振動基頻。

2.1 耗能器參數的影響

首先,為考慮速度指數α0和結構基本周期T變化的影響,圖4 給出了部分減震結構的地震響應曲線。其中,x0和xd分別為無控結構和減震結構的相對位移;和為其對應的絕對加速度; xv為阻尼器相對于結構的位移。

現以附加阻尼比ξ1=10%為例進行詳細探討分析。其中,圖4a ～4c 為減震結構與無控結構的位移之比隨kb/(cdω)變化的曲線。從圖中可知,當線性粘滯阻尼器(α0=1.0)的支撐剛度滿足kb/(cdω)≥3 時,減震結構的位移減震效果相對趨于穩定,這與抗規[1]給定的適用范圍基本一致; 但對于非線性粘滯阻尼器(0.3 ＜α0＜1.0),隨著α0的減小,結構附加阻尼器的減震效果隨kb/(cdω)的增大而更加顯著,表明需要增大kb/(cdω)的值才能使阻尼器的減震作用得到最大程度的發揮,這一特點隨著結構自振周期逐漸增大時更為明顯。圖4d ～4f 為減震結構與無控結構的絕對加速度之比隨kb/(cdω)變化的曲線。從圖中可知,kb/(cdω)對減震結構加速度的影響也存在上述類似的規律。

圖4 在不同α0 和T 值條件下參數kb/(cdω) 對結構地震響應(位移和加速度)的影響Fig.4 Effect of parameter kb/(cdω) on the seismic responses (displacement and acceleration) of SDOF structure with viscous dampers under different conditions of α0 and T

圖4g ～4i 為阻尼器與減震結構的位移之比隨kb/(cdω)變化的曲線。由圖可知,當線性粘滯阻尼器(α0=1.0)滿足條件kb/(cdω)≥3 時,該位移比值均在0.9 以上,表明阻尼器的位移已基本接近于減震結構的位移,支撐剛度變形很小,此時阻尼器得到最大程度利用。當α0逐漸減小時,該位移比值在相同值kb/(cdω)下逐漸減小,表明支撐剛度的變形在逐漸增大,此時需要增大kb/(cdω)的值才能夠使阻尼器的減震作用得到充分發揮。同時發現,kb/(cdω)對減震結構地震響應的影響規律隨結構自振周期的變化而有微小波動。

此外,為說明附加阻尼比ξ1增加對結構位移和加速度的影響,圖5 給出了減震結構在不同阻尼水平下的地震響應隨kb/(cdω)變化的曲線,此處暫不考慮α0對ξ1的影響。

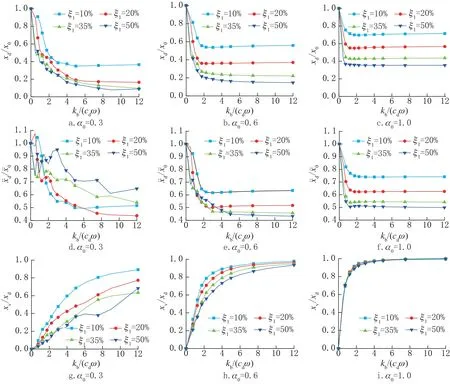
圖5 在不同ξ1 值條件下參數kb/(cdω)對結構地震響應(位移和加速度)的影響(T=0.5s)Fig.5 Effect of parameter kb/(cdω) on the seismic responses (displacement and acceleration) of SDOF structure with viscous dampers under different conditions of ξ1

其中,圖5a ～5c 為減震結構與無控結構的位移之比隨kb/(cdω)變化的曲線。通過對比可知,對于線性粘滯阻尼器,當kb/(cdω)≥3 時,結構的位移減震效果基本趨于穩定,且不受阻尼系數cd取值變化的影響; 但對于非線性粘滯阻尼器,α0越小時則需要kb/(cdω)的值越大才能使阻尼器的減震作用得到充分發揮,這一特性隨著ξ1值的增大而更加明顯。圖5d ～5f 為減震結構與無控結構的絕對加速度之比隨kb/(cdω)變化的曲線。從圖中可知,ξ1取值變化對減震結構加速度的影響也存在上述類似規律。

圖5g ～5i 為阻尼器與減震結構的位移之比隨kb/(cdω)變化的曲線。通過對比可知,當kb/(cdω)一定時,對于線性粘滯阻尼器而言,xv/xd的比值基本不受ξ1取值變化的影響; 而對于非性粘滯阻尼器,隨著ξ1的增大(或α0的減小),xv/xd的比值逐漸減小,表明阻尼器與結構之間的相對位移在不斷增大,阻尼器的支撐剛度不足,需要增大kb/(cdω)才能減小阻尼器與結構之間的相對位移,保證阻尼器充分發揮減震作用。

2.2 結構非線性的影響

此外,為進一步考慮結構非線性因素的影響,現以T =1.2s,α0=0.3 為基礎,分析減震結構在不同彈塑性狀態下的地震響應隨kb/(cdω)變化的規律,部分結果如圖6 所示。

圖6a 給出了減震結構在進入不同程度彈塑性狀態后的地震響應。由圖可知,當kb/(cdω)≥6 時,減震結構的位移和加速度響應基本趨于穩定,受參數R 變化的影響較小。圖6b 給出了減震結構屈服后剛度對地震響應的影響。由圖可知,當α1在0.02 到0.20 之間變化時,減震結構的地震響應在kb/(cdω)≥6 的條件下也基本趨于穩定。

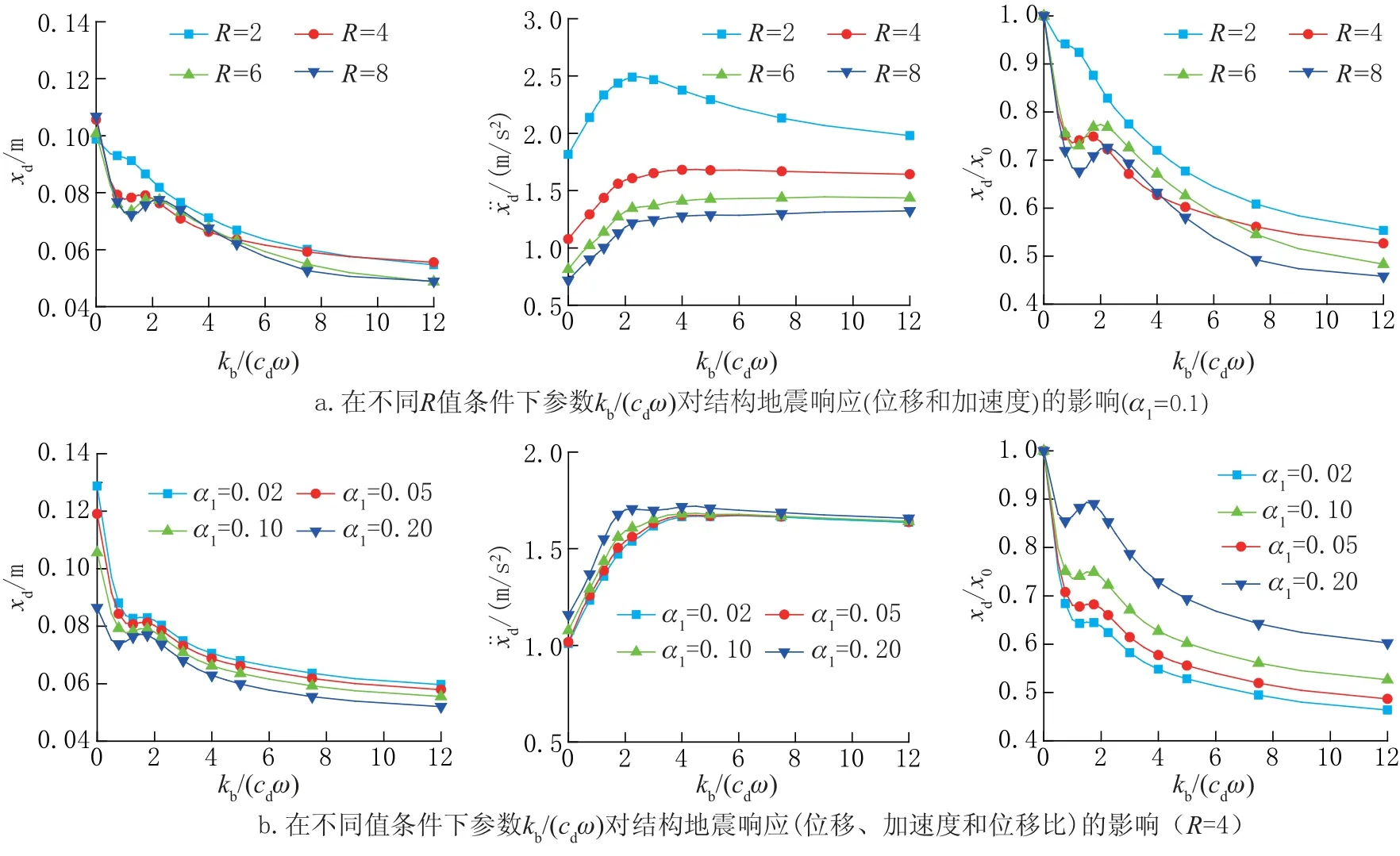
圖6 不同非線性條件下參數kb/(cdω)對結構地震響應的影響Fig.6 Effect of parameter kb/(cdω) on the seismic responses of SDOF structure with viscous dampers under different conditions of structural nonlinearity

綜合考慮上述各因素的影響,建議當結構附設線性粘滯阻尼器時,抗震規范給出的支撐剛度在滿足kb/(cdω) ≥3 的條件下,可以使阻尼器的減震作用得到充分發揮; 但對于非線性粘滯阻尼器,則需要進一步增大kb/(cdω)的值才能使阻尼器的減震作用得到充分發揮。建議當α0等于0.3 時,kb/(cdω) 的取值應不小于6; 當 α0在0.3 到1.0 之間時,kb/(cdω)可根據 α0的取值在3 到6 之間通過線性內插來確定。

3 減震效果影響分析

為說明上述分析結論的適用性和準確性,現以7 層的鋼筋混凝土框架結構為對象進行分析,其抗震設防烈度為8 度0.2g,設計地震分組為第一組,Ⅱ類場地。結構各層層高均為3.6m,其中X 方向為4 跨(邊跨6.0m、中跨7.2m),Y 方向3 跨(邊跨6.4m、中跨4.8m)。1 ～3 層柱截面尺寸為600mm×600mm,4 ～7 層柱截面尺寸為500mm ×500mm,梁截面尺寸包括250mm×500mm 和350mm ×700mm,混凝土均采用C30。同時,采用Bilinear 強化模型來考慮結構的非線性特性,各樓層的屈服位移取為層高的1/250,屈服后剛度與屈前剛度之比取為0.05,并利用Matlab 編寫多層非線性結構動力求解程序。

現考慮在結構中設置非線性粘滯阻尼器,根據結構一階模態對應的附加阻尼比ξ1為20%確定各樓層的阻尼系數,具體參數見表1。其中,工況2 中各樓層阻尼器的支撐剛度均為無限大(即kb→+∞),工況3 中各樓層阻尼器支撐剛度的取值根據上述分析結論內插計算得到。同時,采用Ⅱ類場地的Imperial Valley-06 (1979年) 地震波并調幅至400gal 后沿結構單向輸入進行彈塑性動力時程分析,結果如圖7 所示。

表1 阻尼器參數Tab.1 Parameters of dampers

圖7 分別給出了無控結構與減震結構的最大層間位移角和樓層加速度對比結果。從圖中可以看出,無控結構第三層的層間位移角達到最大值,設置粘滯阻尼器后減震效果顯著。圖8 ～圖11分別為結構第三層和第六層的位移、加速度反應時程; 圖12、圖13 為結構第三層和第六層的阻尼力-位移關系曲線。

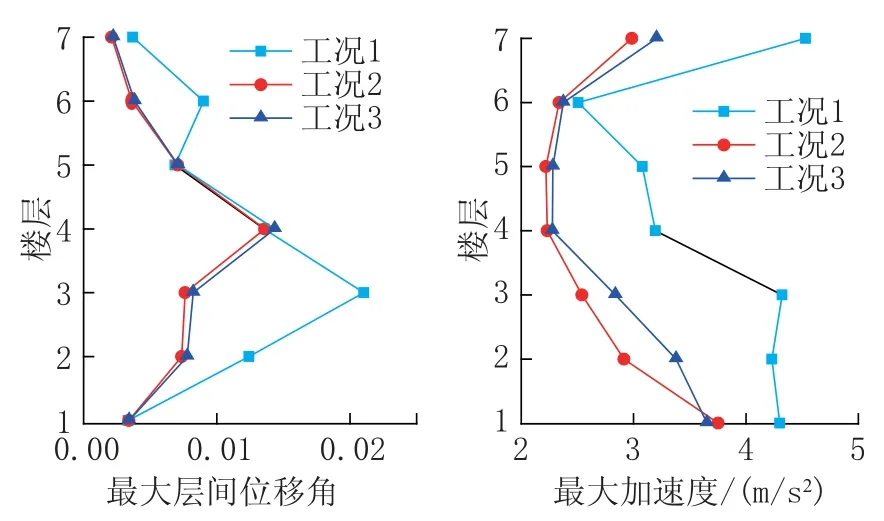
圖7 結構樓層響應Fig.7 Seismic responses of seven-storey structure

圖9 結構第六層位移反應時程Fig.9 Displacement time history response of the 6th floor level

圖10 結構第三層加速度反應時程Fig.10 Acceleration time history response of the 3th floor level

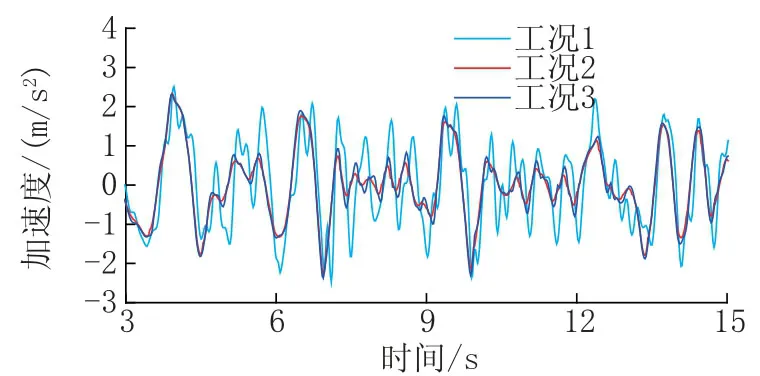
圖11 結構第六層加速度反應時程Fig.11 Acceleration time history response of the 6th floor level

圖12 結構第三層阻尼器的阻尼力-位移關系曲線Fig.12 Damping force-displacement curve of the 3th floor level of the structure

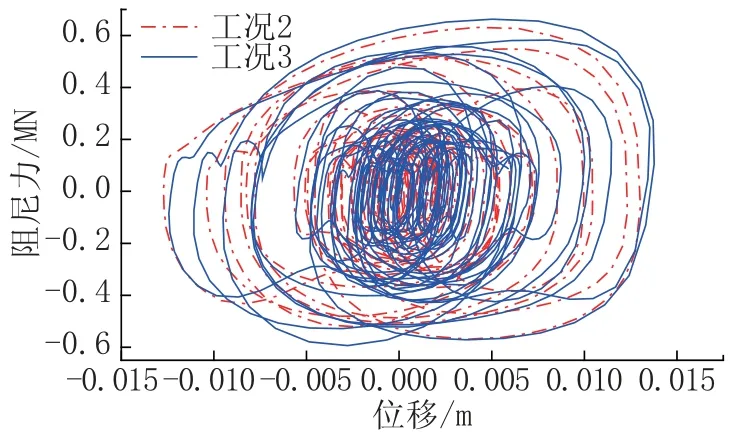
圖13 結構第六層阻尼器的阻尼力-位移關系曲線Fig.13 Damping force-displacement curve of the 6th floor level of the structure

由圖可知,根據本文提出的阻尼器支撐剛度得到的結構地震響應和耗能性能基本接近于支撐剛度無限大的情況,表明該支撐剛度取值的建議可以確保阻尼器的減震作用基本上能夠得到充分發揮,具有較好的工程適用性。

4 結論

1.現行抗震設計規范給出的線性粘滯阻尼器支撐剛度的最小取值范圍能夠保證線性粘滯阻尼器的耗能減震性能得到充分利用,但對于非線性粘滯阻尼器而言,其取值范圍明顯偏小;

2.不同于線性粘滯阻尼器,非線性粘滯阻尼器的阻尼系數cd、速度指數α0對支撐剛度最小取值的影響尤為顯著,而結構非線性、自振周期對其影響相對并不明顯;

3.對于非線性粘滯阻尼器,建議當速度指數α0=0.3 時,kb/(cdω)的取值應不小于6,才能使阻尼器的耗能減震性能基本得到充分利用; 當α0在0.3 到1.0 之間時,kb/(cdω)可根據 α0的取值在3 到6 之間通過線性內插來確定。此支撐剛度的形式與規范相一致,可有效補充抗規關于非線性粘滯阻尼器支撐剛度的規定。