高聳結構位移風振系數

錢昆

(華東建筑設計研究院有限公司 上海200002)

引言

風振系數可分為荷載風振系數和位移風振系數,現行荷載規范采用考慮荷載風振系數的計算方法,只考慮一階振型影響時,位移風振系數與計算點的高度位置無關,給計算帶來方便。以前由位移求內力沒有由外力求位移那么方便,所以規范只列出荷載風振系數,簡稱風振系數,但是隨著有限元軟件的廣泛普及,由位移求內力也變得十分簡單。文獻[1]計算了玻璃幕墻的荷載風振系數和位移風振系數,同時引入等效位移風振系數的概念,證明了荷載風振系數與位移風振系數的內在統一性,并建議對玻璃幕墻這種結構,宜采用荷載風振系數。對于高聳結構,結構設計由結構剛度控制,按照《高聳結構設計規范》(GB50135 -2006)規定,塔頂最大位移不超過塔高的1/100,在滿足這一條件下時,可以初步確定結構的高寬比,所以在高聳結構的選型設計或者初步設計時,僅需通過位移風振系數計算位移作為控制指標。本文詮釋了風振系數的概念,根據隨機振動理論,由位移風振系數的定義,推導出只考慮第一振型影響的表達式,引入一個參數θ,并對其進行參數分析,根據規范給出的振型公式編制出一般截面的空間相關性折算系數和參數θ的計算用表。

1 位移風振系數

工程上常將平均風響應乘以一個系數以表示平均風和脈動風共同作用的總響應,這個系數稱為風振系數,等于風的總響應與平均風產生的響應之比,即：

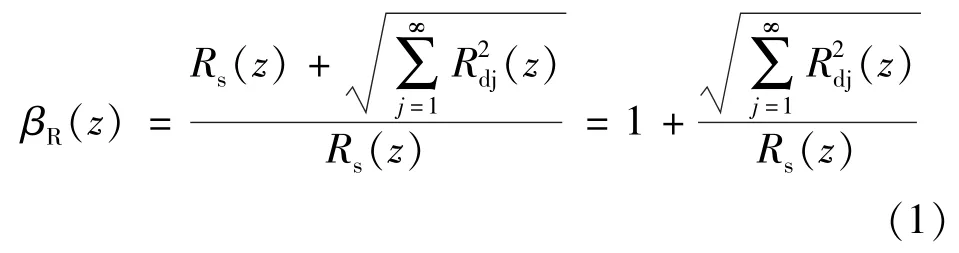
式中： R(z)、Rs(z)、Rd分別代表總響應、平均風的響應、脈動風的響應,分別代表z 高度處的位移、內力或者荷載。隨著R 所表示的意義不同,而有不同的風振系數,如果把R 理解為位移,則可求出位移風振系數。

當僅考慮第一振型時,由動力學知識可得平均風位移表達式[2]為：

式中： us稱為靜力影響系數; w0為基本風壓;ω1為第一振型圓頻率; ?1i為第一振型系數。

2 高聳結構位移風振系數

由位移風振系數的定義[3],可得：

式中： βyi為位移風振系數; ydi為脈動風位移; ξ1為脈動增大系數,μ1為振型系數; m(z)為隨高度變化的線質量; μs(z)、μz(z)、lx(z)、?1(z)、ps(z)分別為z 高度處的風荷載體型系數、風壓高度變化系數、結構寬度、第一振型系數、靜力風荷載。

高聳結構僅考慮豎向相關性,可得：

式中： μf(z)為z 高度處脈動系數; ηz1為一般截面的空間相關性的折算系數; H 為結構高度; μf(z′)、μz(z′)、lx(z′)、?1(z′) 分別為z′高度處的風荷載體型系數、風壓高度變化系數、結構z′高度處的寬度、第一振型系數; ρz為相關性系數。

為方便應用,這里引入一個參數θ,并假定μs(z)為常數; 其表達式如下：

則式(3)可表達為：

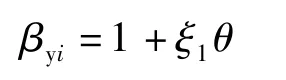
《高聳結構設計規范》(GB50135 -2006)[4]將非等截面變化的高聳結構的體型假定為：

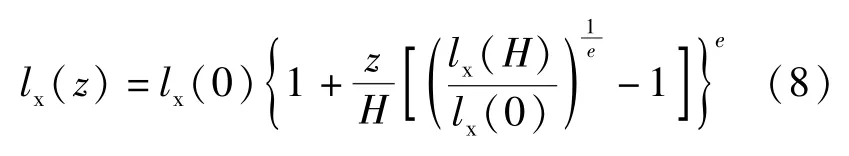
式中：e代表結構外形,e=1、e ＞1、e ＜1 分別代表結構外形為直線、內凹和外凸; lx(H)、lx(0)、lx(z)為結構頂部寬度、底部寬度、z高度處的寬度。

《建筑結構荷載規范》(GB50009 -2012)[5]將地面粗糙度分為A、B、C、D 四類,任意地貌梯度風高度HTa分別取300m、350m、450m、550m,地面粗糙度 α 分別取0.12、0.15、0.22 和0.30,故得風壓高度變化系數：

由《建筑結構荷載規范》(GB50009 -2012)知脈動系數μf(z)為：

式中： g 為峰值因子,可取2.5; I(z)為z 高度處的湍流強度; I10為10m 高度名義湍流強度,對應A、B、C、D 類地面粗糙度,可分別取0.12、0.14、0.23、0.39。

Shiotami 在試驗基礎上,豎向相關系數ρz建議采用只與兩點間距離有關的簡單表達式：

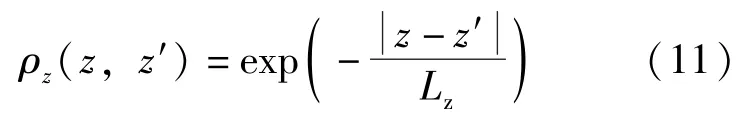
式中： ρz(z,z′)為脈動風壓垂直方向的相干系數;為垂直兩點間的距離。根據試驗資料的統計分析可知,Lz 大部分落在40 ～60 之間,故建議取Lz =50m。對于結構的振型系數?1(z),理應在結構動力分析時確定,為了簡化,荷載規范在確定風荷載時,對等截面高聳結構,采用均布荷載下撓曲線為近似第1 振型,即：

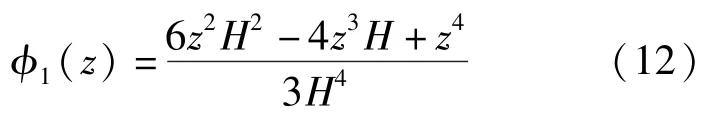
3 計算分析

將式(9)的 μz(z)、式(10)的 μf(z)、式(11)的ρz和式(12)的振型公式代入式(6),采用matlab 編程,可得到ηz1隨結構高度H、結構外形e、lx(H)/lx(0)和地面粗糙度的變化規律,如圖1 所示。可以看出,ηz1受高度影響比較大,其他因素對其均無明顯影響,將ηz1制成表格,如表1 所示。

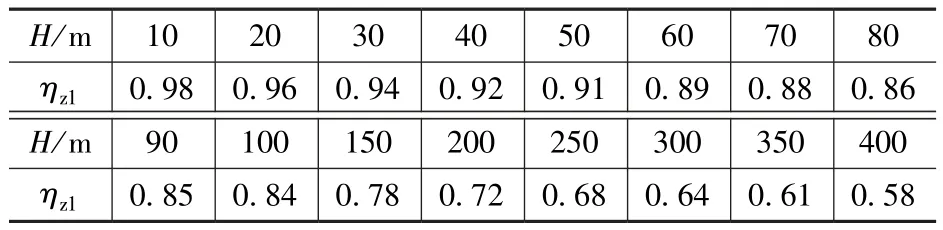
表1 一般截面高聳結構ηz1計算用表Tab.1 Tables for calculation of tall structures with general sections

同樣方法由式(7)可得到θ如圖2 和表2 所示。計算表明,結構的外形e=10 時計算所得結果僅比e=0.25 時大約3%,lx(H)/lx(0) =0.1的計算結果也僅比lx(H)/lx(0) =1.0 時的計算結果大5%左右,故可忽略它們對θ的影響。式(7)的分子中多了一項脈動系數,主要由地面粗糙度決定,ηz1主要由高度決定,所以θ主要由地面粗糙度和高度決定。

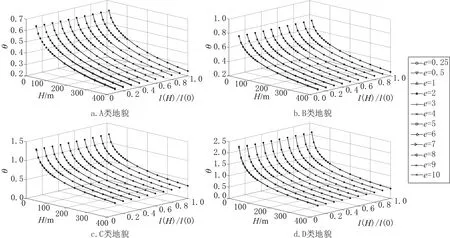
圖2 系數 θ=μ1/μs1Fig.2 Coefficient θ=μ1/μs1

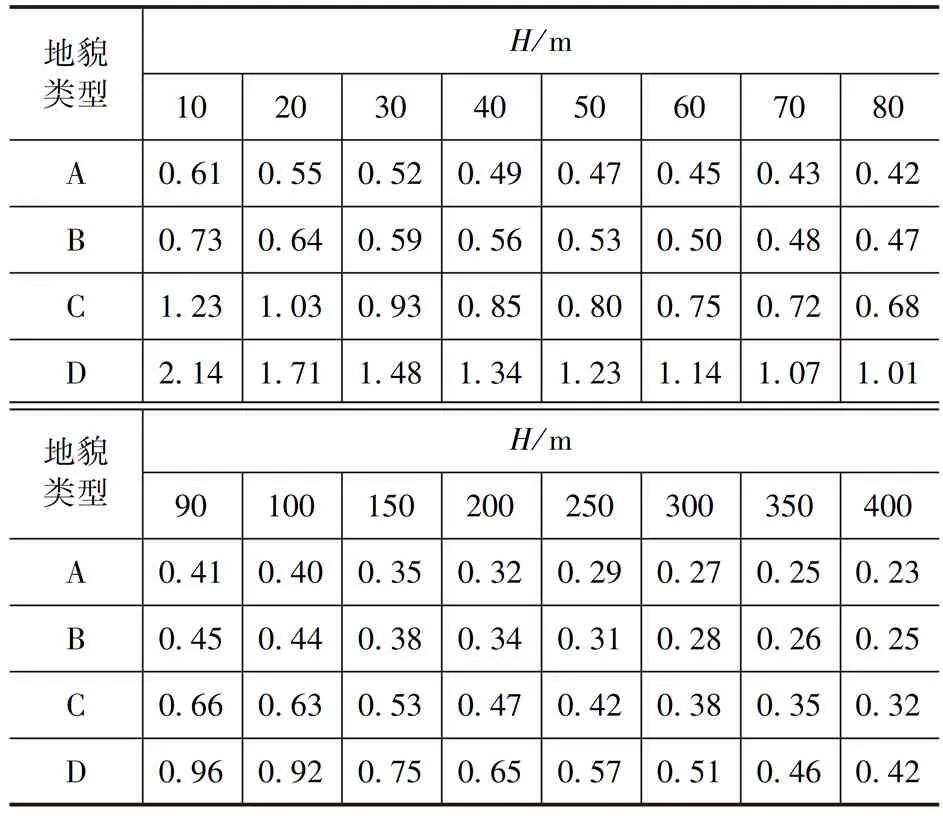
表2 一般截面高聳結構θ 計算用表Tab.2 Tables for calculating tall structures with general sections

4 結論

1.僅考慮第一振型時,根據隨機振動理論,推導出高聳結構位移風振系數的一般表達式。

2.對空間相關性折算系數ηz1及參數θ進行編程分析,ηz1受高度影響比較大,結構外形e、lx(H)/lx(0)和地面粗糙度對其均無明顯影響;θ主要由地面粗糙度和高度決定,結構外形e和lx(H)/lx(0)對其無明顯影響。

3.將θ制成關于地面粗糙度和結構高度的表格,從而求出高聳結構位移風振系數,方便相關工程應用。