波形鋼腹板組合曲線箱梁的撓度偏載系數(shù)分析?

丁漢山 蔣勇

(東南大學土木工程學院 南京211189)

引言

波形鋼腹板箱梁橋是20 世紀末出現(xiàn)的一種新型的鋼-混組合結(jié)構(gòu)橋梁,因其具有較好的受力性能及便于運輸安裝等優(yōu)點,在我國鋼結(jié)構(gòu)橋梁建設(shè)中占據(jù)重要地位。與混凝土曲線梁橋相比,用波形鋼板替代混凝土腹板,降低了結(jié)構(gòu)自重,提高了腹板的抗剪性能及結(jié)構(gòu)耐久性[1-4]。對于波形鋼腹板曲線箱梁因腹板厚度較薄,由鋼腹板剪切效應產(chǎn)生的撓度變形較混凝土箱梁將增大10% ～30%左右[5],同時在彎扭耦合作用下,箱梁在偏載作用下產(chǎn)生的撓度變形也會更加明顯[6]。

對于薄壁箱梁的撓度計算,國內(nèi)外已有學者進行過相關(guān)研究。Taniguchi 在疊合梁理論上推導出波形鋼腹板組合梁的撓度計算公式[7]。Kato.H等引入兩個獨立的位移函數(shù)建立截面平衡方程,得到了波形鋼腹板組合梁的撓度計算公式[8],利用矩陣位移法求解擴大了理論的應用范圍。國內(nèi)陳玉驥、羅旗幟等人根據(jù)薄壁曲線梁理論和勢能變分原理,推導出薄壁曲線箱梁在彎、扭、剪力滯耦合時的曲線箱梁幾何非線性控制微分方程,再采用同倫延拓法可求得結(jié)構(gòu)在荷載作用下的半解析解[9]。甘亞南、周廣春以薄壁曲桿理論為基礎(chǔ),提出一種對曲線梯形箱梁靜力學特性準確分析的解析法,提高了該類結(jié)構(gòu)應力和撓度計算精度[10]。

目前,對于曲線箱梁在荷載作用下?lián)隙茸冃蔚难芯?腹板多采用混凝土澆筑,對于波形鋼腹板曲線箱梁的偏載撓度研究鮮有報道。為此,本文以薄壁曲線梁理論和能量變分原理為基礎(chǔ),推導曲線箱梁橋的變形控制微分方程,并設(shè)計3 片試驗曲梁,驗證曲線箱梁橋偏載理論模型的正確性,對波形鋼腹板組合曲線箱梁的設(shè)計計算提供參考。

1 波形鋼腹板曲線箱梁受力分析

對波形鋼腹板組合曲線箱梁進行受力分析時,可采用曲桿結(jié)構(gòu)力學及薄壁箱梁理論分析其受力性能,揭示作用力傳遞機理及各因素之間的影響關(guān)系。

圖1 為實際工程中應用最廣的單箱單室波形鋼腹板組合曲線梁截面結(jié)構(gòu)。z、y、x為通過截面形心軸向、豎向和徑向坐標;hc為波形鋼腹板高度;tw為波形鋼腹板厚度。假定混凝土箱梁頂?shù)装遑Q向纖維間無相互擠壓,忽略混凝土頂?shù)装迤矫嫱獾募魬兗皺M向正應變,波形鋼腹板與混凝土頂?shù)装逶趶椥噪A段時不產(chǎn)生相對滑移,剪力全部由波形鋼腹板承擔。

從力學角度分析,結(jié)構(gòu)在荷載作用下的彈性位移由彎曲變形、軸向拉伸和剪切變形組成,在傳統(tǒng)混凝土曲線梁橋中腹板剪切變形產(chǎn)生撓度較小,一般可忽略不計。對于波形鋼腹板曲線組合箱梁,鋼腹板抗剪面積較小,腹板產(chǎn)生的剪切應變能不可忽略。

為求出波形鋼腹板剪切應變能,在縱向位移函數(shù)中引入剪應變函數(shù),見式(1),假定腹板剪應力沿高度方向均勻分布,則腹板位置任意微元體剪應變方程可表示為：

式中：Q(x)為波形鋼腹板的豎向剪力;Aw為波形鋼腹板截面面積;k為剪切形狀系數(shù);Ge為波形鋼腹的有效剪切模量,根據(jù)Johnson R P 等[11]試驗證明,其計算公式可表示為：

式中：b和d分別為波形鋼腹板的水平板寬和斜板寬;α為波形鋼板的折疊角;G為鋼板的剪切模型。

圖1 波形鋼腹板箱梁截面Fig.1 Section of box girder with corrugated steel webs

則波形鋼腹板的剪切應變能為：

式中：V為波形鋼板的微段體積;z為波形鋼板軸向長度;As為波形鋼腹板的面積。

在偏載作用下箱梁空間應力分析較為復雜,當箱梁設(shè)置足夠數(shù)量橫隔板時,畸變變形可忽略不計,故計算薄壁箱梁橫截面上任意點的應力時,考慮彎曲和扭轉(zhuǎn)效應即可。

箱梁在發(fā)生縱向彎曲時,箱梁截面上將產(chǎn)生縱向彎曲正應力σM和縱向彎曲剪應力τM,如圖2所示。

圖2 箱梁縱向彎曲時截面應力圖Fig.2 Stress diagram of section of box girder under longitudinal bending

箱梁的剛性扭轉(zhuǎn)可分為自由扭轉(zhuǎn)和約束扭轉(zhuǎn),箱梁自由扭轉(zhuǎn)時,截面上縱向翹曲不受約束,因而截面上不產(chǎn)生縱向正應力,僅產(chǎn)生自由扭轉(zhuǎn)剪應力τk,如圖3a 所示; 當箱梁縱向變形受到約束,在截面上同時產(chǎn)生約束扭轉(zhuǎn)正應力σω和約束扭轉(zhuǎn)剪應力τω,見圖3b、3c。

圖3 箱梁剛性扭轉(zhuǎn)時截面應力圖Fig.3 Section stress diagram of box girder under rigid torsion

對于波形鋼腹板曲線箱梁因彎扭耦合效應存在,在豎向荷載作用下箱形梁橫截面和縱截面上應力為：

根據(jù)葉見曙等[12]波形鋼腹板箱梁截面變形研究,截面縱向應變符合“擬平截面假定”,忽略鋼腹板的彎曲應變能,則波形鋼腹板組合曲線箱梁的彎曲應變能為：

式中：v″為截面的豎向位移引起的轉(zhuǎn)角;γ′為波形鋼腹板剪應變引起的轉(zhuǎn)角;φ為截面繞剪切中心轉(zhuǎn)角;EI為截面的抗彎剛度;R為曲線梁的曲率半徑。

為了準確表達波形鋼腹板曲線箱梁的翹曲位移,在符拉索夫采用截面扭角的一階導數(shù)作為翹曲廣義位移基礎(chǔ)上,引入獨立的扭轉(zhuǎn)翹曲廣義位移函數(shù)β,則曲線梁截面的翹曲位移表達為：

式中：v′為截面的豎向應變;γ為波形鋼腹板剪應變;ω為廣義扇形坐標。

任一微段截面翹曲正應力應變能為：

式中：Bω為截面翹曲雙力矩;Iω為廣義扇形慣性矩;β′為扭轉(zhuǎn)翹曲廣義轉(zhuǎn)角的一階導數(shù)。

波形鋼腹板箱梁截面在扭轉(zhuǎn)剪應力作用下,箱壁微元會發(fā)生圖4 所示變形。其中,us表示箱梁壁厚中心線的環(huán)向坐標,uw表示形心軸曲線坐標。

圖4 箱壁微元扭轉(zhuǎn)變形Fig.4 Torsion deformation of box wall element

則曲線梁頂?shù)装褰孛媾まD(zhuǎn)剪應變γτ：

式中：ρ為截面扭轉(zhuǎn)中心到箱壁上任一點切線的距離;φ′為截面扭轉(zhuǎn)角在軸向的一階導數(shù)。

波形鋼腹板曲線梁約束扭轉(zhuǎn)總應變能Uτ可由自由扭轉(zhuǎn)應變能Us和約束扭轉(zhuǎn)應變能Uw相加表示：

式中：Iρ為箱梁截面極慣性矩;Id為截面抗扭慣性矩。

式中：Ω為箱壁圍成面積的2 倍;t為箱形截面的壁厚;A為箱壁所圍的截面面積;s為箱梁截面周邊位移的長度。

從而將波形鋼腹板的彎曲應變能UM、腹板剪切應變能Uf、翹曲正應力應變能Uω及扭轉(zhuǎn)剪應力應變能Uτ相加即可得到結(jié)構(gòu)總應變能U：

根據(jù)最小勢能原理,當結(jié)構(gòu)處于平衡狀態(tài)時,系統(tǒng)總勢能取極小值,一階變分為零：

式中：V為外荷載勢能;v為曲線箱梁在豎向荷載作用下位移;m為分布扭矩;q為梁縱向分布荷載。

波形鋼腹板曲線箱梁的總勢能為：

由最小勢能原理可知δΠ =0,利用伽遼金法對式(18)進行泛函變分求解,即可求得波形鋼腹板曲線箱梁變形分析的控制微分方程：

設(shè)各待求解位移及應變的函數(shù)為：

根據(jù)伽遼金法求解波形鋼腹板曲線箱梁控制微分方程,即可得到箱梁各截面的應力及變形結(jié)果。

對于波形鋼腹板曲線箱梁在豎向荷載作用下的內(nèi)外側(cè)撓度,可利用式(21)進行計算,即：

式中：vW表示試驗梁外側(cè)底板撓度;vN表示試驗梁內(nèi)側(cè)底板撓度;B2示試驗梁1/2 底板寬度。

2 試驗驗證

2.1 試驗模型

為驗證上述曲梁的撓度偏載理論,制作了3片波形鋼腹板組合曲線梁,分別為試驗梁L1 -2、L2 -2 和L2 -3。根據(jù)試驗目的,除橫隔板數(shù)量與腹板厚度不同外,試驗梁頂?shù)装宄叽缂安牧闲阅芤恢?見表1。

表1 試驗梁參數(shù)Tab.1 Test beam parameter table

試驗梁橫截面尺寸如圖5所示。試驗梁為單跨等截面箱梁(單箱單室),全長為6600mm,計算跨徑為6400mm,曲率半徑為8000mm。實測材料性能參數(shù)： 鋼纖維混凝土抗壓強度平均值fck=26.8MPa,彈性模量Ec=32.5GPa; 試驗梁鋼筋均采用II 級帶肋鋼筋,腹板及中橫隔板采用Q235鋼板,彈性模量Es= 180GPa,泊松比為0.3,波形鋼腹板剪切形狀系數(shù)量k=1,有效剪切模量Ge=G/1.1。

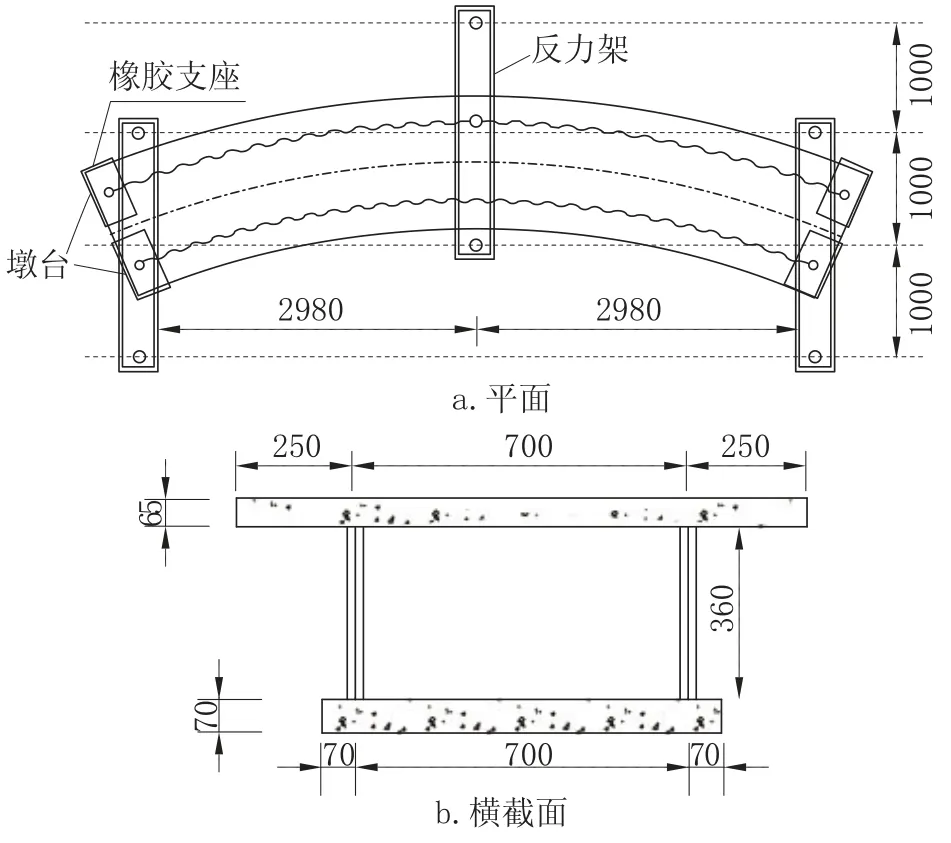
圖5 試驗梁幾何尺寸(單位： mm)Fig.5 Geometric dimensions of test beam (unit： mm)

波形鋼腹板與混凝土頂?shù)装褰Y(jié)合部采用嵌入式剪力連接鍵,通過穿筋焊接于連接鋼板,確保在試驗荷載作用下腹板與混凝土頂?shù)装鍩o相對滑移產(chǎn)生。

為研究試驗曲梁在偏心荷載作用下,底板內(nèi)外側(cè)撓度的變化規(guī)律,在試驗梁的端支座、1/4L、1/2L、3/4L截面底板內(nèi)外側(cè)均布置電阻式位移計,測點布置如圖6 所示。

圖6 試驗梁底板應變測點布置Fig.6 Strain measurement point layout of the bottom plate of the test beam

2.2 試驗加載

試驗梁加載采用千斤頂配合分配梁形式進行集中荷載的分級加載,加載方式可見圖7a ～7c。

圖7 試驗裝置布置圖Fig.7 Arrangement of test beam equipment

由于文中撓度求解理論建立在材料線彈性基礎(chǔ)上,為將試驗實測值與理論值進行對比分析,文中加載工況分為彈性范圍內(nèi)跨中單點內(nèi)側(cè)、跨中單點外和跨中雙點加載側(cè)加載三種加載方式。

試驗加載分5級加載,每級加載穩(wěn)定讀數(shù)2min后,記錄對應實際荷載及撓度數(shù)據(jù),具體試驗布置和測試方案如圖7d ～7e 所示。

3 試驗及結(jié)果分析

采用有限元分析法對試驗梁的加載工況進行完全仿真,利用ANSYS 建立試驗梁整體式有限元模型。試驗梁混凝土頂?shù)装宀捎肧OLID45 三維實體單元,波形鋼腹板厚度較薄則采用SHELL181 板殼單元,梁體普通配筋采用LINK8單元。

考慮到嵌入式抗剪連接件通過焊接相連,剛度大、變形小,頂?shù)装迮c腹板之間的相對滑移可忽略不計,通過結(jié)點耦合近似模擬兩者之間抗剪連接鍵作用。支座處施加相應的面約束模擬橡膠支座,試驗梁的有限元模型如圖8 所示。

圖8 試驗梁有限元模型Fig.8 Finite element model of test beam

根據(jù)有限元模擬分析,試驗梁的開裂荷載約為60kN,因此本文彈性加載階段施加的荷載最大值為50kN,在試驗加載過程中,試驗梁底板未有可查裂縫出現(xiàn)。

試驗加載為集中加載,為避免加載點截面應力集中的影響,實測值以L/4 截面為準。圖9 為試驗梁L1 -2、L2 -2 和L2 -3 在跨中雙點加載作用下,L/4 截面底板的撓度實測值、有限元值和理論分析值。其中,撓度實測值取所測截面內(nèi)外側(cè)撓度均值。圖9 表明,荷載-位移曲線基本呈線性變化,三條曲線吻合度良好,利用能量變分法求得的理論解析解與試驗值、有限元值較為接近,驗證了理論計算和有限元模型的正確性。

圖9 跨中雙點加載試驗梁L/4 截面底板撓度值Fig.9 Deflection value of bottom plate of L/4 section of test beam under mid-span double-point loading

表2 為波形鋼腹板曲線梁L/4 截面的底板撓度均值,由表可知： ①三片試驗梁在跨中雙點加載工況下,實測值都大于有限元和理論值,這主要是因為所建立的有限元整體式模型與試驗梁有差異,試驗梁材料因初始缺陷在加載過程中剛度降低; ②從三片試驗梁底板撓度對比可知,腹板厚度對撓度變形影響較大,而橫隔板數(shù)量對撓度影響可以忽略不計。

表2 試驗梁L/4 截面底板內(nèi)外側(cè)撓度均值Tab.2 Average deflectionvalue of L/4 section floor of test beam

4 波形鋼腹板曲線箱梁撓度偏載系數(shù)分析

為研究波形鋼腹板組合曲線箱梁的撓度偏載效應,本文以四川綿茂東河3 號橋為計算模型,利用文中箱梁撓度計算理論對其進行相關(guān)分析。此橋上部結(jié)構(gòu)為兩跨波形鋼腹板預應力混凝土箱梁,橋梁跨徑布置為80m + 80m,兩跨平面分別位于半徑為256m 和半徑310m 的圓曲線上,本文模型梁僅取其中半徑為256m 的一跨,邊界條件為簡支約束進行偏載分析。

主梁采用單箱單式截面。雙車道橋面寬為9m,底板寬為5m,箱梁懸臂翼緣2m,懸臂板端部厚度為20cm,根部厚度為60cm,尺寸詳圖見圖10。箱梁混凝土采用C40 混凝土,波形鋼腹板鋼材選用Q345C,厚度10mm,波長160cm,波高22cm,水平面板寬43cm,折疊角度為30.7°,見圖11。

圖10 箱梁截面尺寸(單位： cm)Fig.10 Section size of box beam (unit： cm)

圖11 梁橫截面及腹板尺寸Fig.11 Size of cross section and web

參照《公路橋涵設(shè)計通用規(guī)范》中關(guān)于公路-I 級車道荷載規(guī)定,計算荷載由均布荷載qk=10.5kN/m 和集中荷載Pk=360kN 組成。改變模型幾何參數(shù),計算箱梁跨中底板撓度值,研究各參數(shù)變化對撓度偏載系數(shù)的影響。

對于波形鋼腹板曲線箱梁,因曲率半徑存在,箱梁的外側(cè)弧長大于內(nèi)側(cè)弧長,結(jié)構(gòu)重心偏向于曲線外側(cè),在自重作用下,箱梁外側(cè)撓度大于內(nèi)側(cè)撓度。文中撓度偏載系數(shù)定義為：

4.1 曲率半徑對偏載撓度的影響

結(jié)合公路和城市立交彎橋的設(shè)計需求,保持橋梁跨徑L=80m,曲線梁的半徑取值為120m ～300m,以20m 幅度為增量單位研究波形鋼腹板曲線梁在偏載作用下,曲率半徑變化對撓度偏載系數(shù)的影響。曲線梁在內(nèi)、外側(cè)偏心荷載作用下跨中底板撓度偏載系數(shù)如圖12 所示。

從圖12 可以看出： ①在偏載作用下,波形鋼腹板曲線箱梁的撓度偏載系數(shù)都隨著曲率半徑的增大而逐漸減小,但撓度偏載系數(shù)值皆大于1,說明曲線梁在偏載時外側(cè)底板撓度大于內(nèi)側(cè)撓度; ②當曲率半徑大于200m 以上時,隨著曲率半徑的增大,外側(cè)偏載產(chǎn)生的撓度偏載系數(shù)曲線變化趨于平緩穩(wěn)定,變化幅值在2%以內(nèi),可認為此時波形鋼腹板曲線梁扭轉(zhuǎn)變形與直線梁相差無幾,可按直線梁進行計算。

4.2 寬跨比B/L 對偏載撓度的影響

為研究箱梁寬跨比對波形鋼腹板曲線組合箱梁撓度偏載系數(shù)的影響,保持橋梁跨徑L=80m不變,箱梁的寬度尺寸依次取為： 8m ～17m,以1m 幅度為增量單位,其余尺寸不變,內(nèi)外側(cè)偏載作用下產(chǎn)生的撓度偏載系數(shù)值如圖13 所示。

從圖13 可以看出,隨著寬跨比的增加,外側(cè)偏載作用下產(chǎn)生的偏載系數(shù)逐漸增大,而內(nèi)側(cè)偏載作用下產(chǎn)生的偏載系數(shù)逐漸減小,可認為箱梁寬度對曲線梁外側(cè)扭轉(zhuǎn)變形影響較大。

4.3 高跨比H/L 對偏載撓度的影響

取箱梁的腹板高度為2m ～5m,以0.3m 為增量,保持橋梁跨徑L=80m 不變,研究波形鋼腹板曲線箱梁在高跨比0.025 ～0.0625 變化時,內(nèi)外側(cè)偏載產(chǎn)生的偏載系數(shù)情況。圖14 為采用本文理論求得的計算結(jié)果。

圖12 曲率半徑R-撓度偏載系數(shù)ηFig.12 Deflection deflection coefficient of radius of curvature

圖13 寬跨比B/L-撓度偏載系數(shù)ηFig.13 Deflection coefficient of B/L-deflection ratio of width to span

圖14 高跨比H/L-撓度偏載系數(shù)ηFig.14 Deflection coefficient of B/L-deflection ratio of width to span

從圖14 可得： ①在外側(cè)偏載作用下,波形鋼腹板曲線箱梁的撓度偏載系數(shù)隨著高跨比的增大而逐漸增大; ②在內(nèi)側(cè)偏載作用下,當曲線箱梁的高跨比在0.025 ～0.0625 變化時,撓度偏載系數(shù)維持在1.01 附近不變。

5 結(jié)論

本文進行了波形鋼腹板組合曲線箱梁的偏心內(nèi)外側(cè)加載試驗,建立了模型梁的整體式有限元模型,對其受力過程進行了線彈性分析,試驗值與計算值較為吻合,驗證了本文計算方法與有限元模型的正確性,并得出以下結(jié)論：

1.在集中荷載作用下,波形鋼腹板曲線箱梁豎向撓度與腹板厚度有關(guān),與橫隔板數(shù)量無關(guān)。

2.波形鋼腹板曲線箱梁的撓度偏載系數(shù)都隨著曲率半徑的增大而逐漸減小,曲線梁的外側(cè)底板撓度大于內(nèi)側(cè)撓度。

3.曲率半徑大于200m 以上時,外側(cè)偏載產(chǎn)生的撓度偏載系數(shù)曲線變化趨于平緩穩(wěn)定,變化幅值在2%以內(nèi),可按直線梁進行計算。

4.在外側(cè)偏載作用下,波形鋼腹板曲線梁的撓度偏載系數(shù)與箱梁的寬跨比、高跨比呈正相關(guān)。