考慮地震損傷的RC 框架構件滯回模型研究?

李英民 周上鑒 劉杰東

(1.重慶大學土木工程學院 400045; 2.山地城鎮建設與新技術教育部重點實驗室(重慶大學) 400045;3.重慶市聚友建設工程有限公司 400045)

引言

工程結構抗震性能評估的基礎和關鍵在于合理確定結構數值計算模型。遭受地震作用后受到損傷破壞的鋼筋混凝土框架結構在經歷較強的二次地震作用時,其抗震能力可能迅速降低直至結構破壞[1,2]。同時,地震損傷導致構件的強度、剛度等力學性能發生不同程度的退化,從而使其計算模型相較于新建結構發生較大變化。因此對震損結構進行抗震性能評估的前提在于合理的數值計算模型參數。

迄今國內外對鋼筋混凝土框架結構滯回模型研究成果較多,但其中較為成熟的研究及成果大多針對新建結構或未考慮結構的損傷[3-6],近年來關于震損結構滯回模型的研究雖逐漸增多,但仍存在一些尚未解決的問題。歐進萍等[7]在確定地震受損構件恢復力骨架線時,構件受損后屈服位移和屈服力的確定存在一定的多樣性。按周小龍[8]方法采用47 組構件試驗數據擬合出的關系式,數據樣本量偏少,擬合時未考慮軸壓比及體積配箍率等常見參數的影響,且未進行滯回模型合理性及必要性驗證。李洪泉等[9]提出的鋼筋混凝土壓彎構件強度損傷模型需先分別測得無損構件和受損構件的動力特性,才能確定損傷指數D值取值,因此該方法在實際工程應用中存在不便。而賈益綱等[10]采用基于三維虛擬層合單元理論的分析方法建立了3 種不同框架柱軸壓比的框架模型,并分別取單榀框架進行抗側性能分析,得出軸壓比越大,框架抗側移剛度退化速率越快。Zhai 等[11]從統計學角度出發研究得出,強震后余震對結構的影響取決于結構周期、延性系數、余震強度等,且對短周期結構強度折減系數的影響比長周期結構強。Yan 等[12]考慮引起損傷的循環加載次數和控制位移影響,提出了量化地震破壞和衰減系數的方法,并將試驗骨架曲線簡化為三線性模型。郭宗明等[13]在不考慮混凝土拉壓損傷影響及縱筋非彈性屈曲效應的前提下,基于剛度退化和纖維單元建立的損傷模型避免了多次引入加權系數導致的損傷指數在轉化過程中的不確定性。趙志鵬等[14]通過對比分析國內外典型RC 構件損傷模型,認為Park-Ang 損傷模型更適用于RC 柱。

本文在文獻[8]的基礎上,基于不同震損狀態的鋼筋混凝土構件數值計算模型,采用非線性回歸分析方法對美國太平洋地震工程研究中心(PEER)提供的鋼筋混凝土構件低周反復加載的試驗數據進行擬合,得到構造構件損傷程度與剩余強度、剛度等的定量關系,基于適當假定,對震損鋼筋混凝土構件的滯回模型進行確定,并對其進行合理必要性驗證[15],為震損鋼筋混凝土框架結構抗震性能評估提供參考。

1 震損構件滯回參數確定方法

震損鋼筋混凝土框架結構中,構件滯回模型的建立包括選擇地震損傷模型,確定震損構件滯回骨架線和滯回規則三部分[15]。本文采用Park-Ang 模型[16]作為損傷程度的判據,以修正的Ibarra-Medina-Krawinkler 退化模型[17](以下簡稱“修正IMK 退化模型”)定義無損構件與震損構件的滯回規則。

1.1 Park-Ang 損傷模型

Park-Ang 損傷模型反映了最大位移響應與累積滯回耗能相互影響,具有廣泛的應用基礎。表達式如式(1)所示：

式中：D為構件損傷指數; δM為地震作用下構件最大變形; δu為構件單調加載極限變形; β 為能量項加權系數; Qy為計算屈服強度;∫dE 為累積滯回耗能。β 和δu計算公式分別參考文獻[16]和文獻[18]。

1.2 震損構件滯回規則

修正IMK 退化模型[17]通過循環退化指數βi反映震后結構構件的性能退化,震損構件的滯回規則通過對退化模型中反映滯回規則的相應參數進行折減來反映[15]。

式中：c為衰減率指數; Ei為第i 個滯回半圈的滯回耗能;∑Ej為累積滯回耗能;Et為構件滯回耗能能力,按式(3)計算：

式中：Fy為構件的屈服力;δy為構件屈服位移,計算公式參考文獻[19];λ為滯回耗能參數,計算公式參考文獻[20],如下：

式中：n0為構件軸壓比;s為構件箍筋間距; d為截面有效高度; Vp為對應屈服彎矩的剪力值;Vn為構件抗剪強度; ρsh,eff為有效配箍率。

由式(2)和式(3)可知,構件受損后,βi的計算需求得震損構件滯回耗能能力Etd=λdFydδyd,因此,鋼筋混凝土構件震后滯回規則的定義實質在于震損構件滯回耗能參數λd的確定,定義滯回耗能參數退化系數αλ計算公式為：

1.3 震損構件滯回骨架線的確定

1.強度退化系數

強度退化系數反映了構件損傷后的強度退化幅度,其退化規律如式(6)所示[17]：

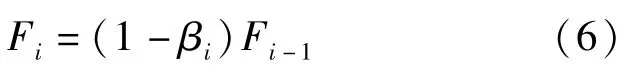
式中：Fi和Fi-1分別表示第i個滯回半圈加載后構件的同向屈服強度。損傷指數為D時,強度退化系數αF計算公式如下：

式中：Fyd為構件損傷指數為D時的屈服強度。2.剛度退化系數

剛度退化系數反映了構件損傷后剛度退化幅度,即：

式中：k0為構件初始剛度;為構件受損后剛度,確定Fyd后,通過幾何關系求得具體數值。

3.震損構件滯回骨架線的確定

確定震損構件退化系數αF和αK后,即可得震損構件滯回骨架線如圖1 所示,確定方法如下[15]：

(1)無損構件骨架線的確定。參考文獻[19]中的經驗公式給出關鍵點參數;

(2)震損構件骨架線彈性上升段的確定。確定構件D及βi,計算其對應的αF和αK,震損構件骨架線彈性上升段由圖中幾何關系確定;

(3)震損構件骨架線屈服后上升段的確定。加載過程中剛度退化規律近似于強度退化規律[17]：/k1=Fyd/Fy,同時假定損傷構件的極限位移近似取為未損傷構件的相應值：xud=xu[7];

(4)震損構件的骨架線下降段的確定。相關研究表明[7,17]損傷構件屈服后下降段剛度與無損時基本一致： 取=k2。

圖1 震損構件恢復力骨架線Fig.1 Hysteretic bone curve of seismic damaged members

1.4 震損構件試驗數據的選取和處理

建立震損結構滯回模型,需對大量構件的試驗結果進行綜合分析。本文所采用的構件低周往復加載試驗值均取自PEER 試驗數據庫,樣本數為97,選取原則為：矩形構件且抗震構造良好,試驗軸力保持恒定或軸力為零,破壞形式為彎曲破壞。97個試件的截面高度、軸壓比、剪跨比等8個參數的平均值、標準差和變異系數見表1。基于工程設計中常用試件參數范圍進行取值,所選試件具有典型代表性。

表1 試件參數統計結果Tab.1 Statistical results of specimen parameters

2 震損構件滯回模型中參數的擬合

本文擬采用MATLAB 軟件編制相關程序,計算得到97 組不同損傷狀態下的αF、αK、αλ,通過回歸分析,擬合損傷指數與各退化系數之間的關系表達式。

2.1 強度退化模型

97 組構件強度退化系數和損傷指數對應關系如圖2 所示。參照整體數據和單獨一組數據的變化規律均能看出,強度退化系數隨損傷指數增大而減小,退化速率先慢后快,呈拋物線變化趨勢,考慮到需滿足邊界條件D=0 時αF=1,經一元非線性回歸分析,得到αF與D擬合關系如下：

圖2 損傷指數與強度退化系數的擬合關系Fig.2 The fitting relationship between the damage index and the degradation coefficient of strength

由式(9)計算得到,當0≤D＜0.4 時,強度退化最大接近10%,式(9)能較為精準地估計強度退化系數。而當0.4 ≤D＜1 時,對應Park等[16]提出的損傷等級,構件處于嚴重破壞階段,數據預測的準確性隨D值增大而減小,當構件破壞程度較嚴重時,由于剩余強度數據離散性較大,此時式(9)適用性較低。

綜合分析導致數據呈發散狀的原因有： (1)式(9)考慮自變量較單一,試件中其他參數如軸壓比、剪跨比等差異性的影響則未考慮; (2)以Park-Ang 震損模型為破壞準則,損傷指數D≠1時,部分試件也可能發生破壞; (3)混凝土材料本身離散型較大及試驗客觀環境不同。因此考慮1.4 節中提到的試件截面高度、軸壓比等8 個基本參數的影響,對式(9)進行改進。由圖2 中強度退化系數隨損傷指數的非線性退化規律,假定改進后的擬合關系式仍為二次拋物線形,設改進后的擬合關系式為：

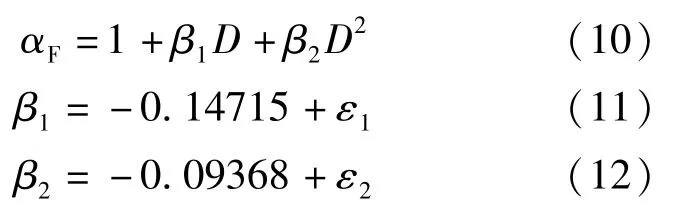
式中：β1、β2為修正后的回歸方程系數;ε1、ε2為考慮設計參數影響的修正系數。

將97 組數據按式(10)進行回歸分析,得到對應β1、β2、ε1、ε2值。以軸壓比、剪跨比等8個參數為自變量,ε1、ε2為因變量,將各數據轉化為符合線性回歸模型的相應數據并以SPSS 統計分析軟件進行回歸分析,篩選出有顯著影響的因素,得到ε1、ε2經驗公式如下：

式中：fyw為箍筋屈服強度;為混凝土抗壓強度;n0為試件軸壓比;ρs為縱筋配筋率。

由式(13)、式(14)可知,對強度退化模型影響較大的參數為試件軸壓比、箍筋屈服強度,其次是縱筋配筋率及混凝土強度。因此,改進后的回歸方程系數擬合式為：

圖3 為其中某單根構件隨加載歷程的不同滯回環數對應的強度退化規律與改進前后擬合曲線的對比情況,可直觀地看出改進后的擬合關系式較好地提高了預測準確度。

圖3 改進前后的擬合關系對比Fig.3 Comparison of fitting relations before and after improvement

2.2 剛度退化模型

同樣通過該擬合過程,計算出各構件剛度退化系數和損傷指數對應關系如圖4 所示,建立D與αK的擬合關系式為：

圖4 損傷指數與構件剛度退化系數的擬合關系Fig.4 Fitting relation between damage index and stiffness degradation coefficient of components

當D=0 時αK=1,此時式(17)滿足邊界條件,且由圖4 可得到式(17)能反映剛度退化隨損傷程度增大的變化規律。此外,R2=0.9,表明式(17)與數據吻合度較好,能較準確地預測構件剛度退化系數。擬合曲線兩側的數據分布均勻且大多集中在曲線附近,離散型小,不需進一步改進擬合關系式。

2.3 滯回耗能退化模型

97組不同損傷狀態下對應的滯回耗能參數退化系數如圖5 所示,建立D與αλ的擬合關系：

圖5 損傷指數與構件滯回耗能參數退化系數的擬合關系Fig.5 Fitting relation between damage index and degradation coefficient of hysteretic energy parameters of components

當D=0 時αK=1,擬合公式滿足邊界條件,R2≈0.9,擬合結果較好,且擬合關系曲線兩側數據分布均勻,離散性小,說明在震損構件損傷指數確定時,根據式(18)能夠得到較為準確的滯回耗能參數退化系數,為確定震損構件滯回模型提供數據參考。

采用擬合式(10)、式(17)、式(18)計算得到的Park-Ang 各損傷狀態界限點的參數退化系數值如表2 所示。

表2 Park-Ang 各損傷界限點的參數退化系數值Tab.2 Parameter degradation coefficient values of damage states boundary points

3 震損鋼筋混凝土框架結構滯回模型合理性驗證

本節分別采用直接分析和間接分析兩種流程對震損結構進行彈塑性時程分析,對比驗證震損結構滯回模型的合理性。直接分析將首尾相連的兩次或多次地震動一次性輸入到無損結構; 間接分析中的初始分析模型取首次地震動輸入后獲得的震損結構,震損構件滯回模型由2.3 節方法得出,隨后再次輸入地震動對結構進行彈塑性時程分析[15]。分析流程如圖6 所示。

圖6 合理性驗證分析流程Fig.6 Flow chart of testing rationality

以二層鋼筋混凝土框架結構為例。模型環境為8 度區,II類場地,地震分組為第二組,丙類結構。材料強度等級：縱筋HRB400,箍筋HRB300,混凝土C35。樓面荷載標準值： 恒載為5kN/m2,活載為2kN/m2,取一榀框架計算,構件截面尺寸與配筋情況如圖7 所示。

利用OpenSees 軟件,采用修正IMK 退化模型通過定義塑性鉸的彎矩-轉角滯回曲線識別震損構件,并分別計算相應震損構件的損傷指數與滯回模型參數,建立震損結構計算模型。對無損結構輸入PGA為0.3g的El-Centro 地震記錄,以結構最大層間位移角為控制指標,得到輕微或中等破壞的震損結構,并對其輸入0.4g的El-Centro波。

圖7 構件截面信息(單位： mm,mm2)Fig.7 Component section information(unit： mm,mm2)

按本節提出的合理性驗證方法對本算例中二層框架結構分別按直接分析、間接分析兩種方法進行彈塑性時程分析,圖8給出了兩種分析方法在二次地震輸入后結構層間位移角時程對比曲線。

圖8 兩種不同方法層間位移角時程對比曲線Fig.8 Comparison between time-history curves of story drift angle in two different ways

由圖8 可知,兩種方法得到的時程曲線基本吻合,變化趨勢保持一致,證明本文提出的滯回模型是合理的。

4 震損RC框架結構滯回模型考慮地震損傷的必要性驗證

以對新建結構輸入地震波得到的震損結構為基礎,建立按本文方法考慮地震損傷的震損模型和不考慮損傷的完好模型。通過再次輸入相同地震波,對兩種計算模型分別進行動力彈塑性分析,得到考慮地震損傷后對計算結果的影響大小,以此驗證采用震損構件滯回模型的必要性,驗證流程如圖9 所示。

圖9 必要性驗證流程Fig.9 Flow chart of testing necessity

對本算例中二層框架進行間接分析,圖10給出了是否考慮震損影響的兩種工況下,結構最大層間位移角的對比情況。

圖10 兩種不同工況最大層間位移角比較Fig.10 Comparison between maximum story drift angle in two different condition

將考慮震損影響與否的層間位移角最大值之差與不考慮震損時層間位移角的比值定義為位移增大率。由圖10 可知,考慮震損情況后,震損結構底層層間位移角減小了8%,二層最大層間位移角增大12%,表明在經歷第二次地震作用時,結構薄弱層由一層變為二層,結構力學性能的退化將影響其地震響應,在設計時亦不容忽視。分析可知,是否考慮地震損傷對結構分析結果影響較大,對震損結構進行動力彈塑性分析時應采用考慮地震損傷影響的滯回模型,從而模擬結構力學性能參數的折減。

5 結論

1.提出了震損構件滯回模型中參數的確定方法和建立滯回模型的基本思路,并給出滯回模型合理性和必要性的驗證方法。

2.考慮軸壓比、剪跨比、配筋率等因素影響下,得到了構件損傷指數與強度、剛度、滯回耗能參數退化系數對應的擬合關系式,提高了剩余強度預測準確度。

3.通過具體算例證明退化模型的合理性和必要性。地震損傷對鋼筋混凝土框架結構的力學性能退化的影響不容忽視,在對震損結構進行動力彈塑性分析時應采用考慮地震損傷的滯回模型。