低空影像SfM三維重建的耦合單-多旋轉平均迭代優化法

何海清，陳 敏，陳 婷，李大軍，陳曉勇

1. 東華理工大學測繪工程學院，江西 南昌 330013； 2. 流域生態與地理環境監測國家測繪地理信息局重點實驗室，江西 南昌 330013； 3. 西南交通大學地球科學與環境工程學院，四川 成都 611756； 4. 東華理工大學水資源與環境工程學院，江西 南昌 330013

低空無人機因具有機動靈活、快速高效、受環境條件制約小等優勢，近年來以其作為平臺的垂直和傾斜攝影測量方式廣泛運用于土地資源調查、城市規劃、災害監測等方面[1-2]。

相比傳統航空航天攝影，低空攝影存在平臺姿態不穩定、影像重疊度不規則等問題[2]，因此，傳統的攝影測量方法難以滿足低空影像處理的需要。其中，影像的外方位元素高精度高效地解算是關鍵技術之一，近年來許多研究人員針對這一關鍵技術展開了廣泛而深入的研究，最具代表性的方法是利用計算機視覺中運動恢復結構(structure from motion,SfM)[3]來恢復影像的位置與姿態參數。SfM算法可通過具有重疊的影像恢復相機的外方位元素，無須任何輔助信息即可重建三維場景，與傳統攝影測量比較，對攝影相機、影像重疊規則性等要求低，且具有自動化程度高和通用性好等優勢，被廣泛應用到低空攝影測量數據處理中[4-9]。

在計算機視覺中，SfM算法通常是利用兩兩匹配遍歷全局影像關聯影像，n幅影像匹配時間復雜度為o(n2)，其三維重建效率低下，不適用于低空攝影測量數據處理需要，低空無人機GPS/IMU信息常被用于輔助SfM算法三維重建[10-13]。文獻[6]利用低空無人機飛控記錄數據構建影像拓撲關系，縮小關聯影像搜索范圍來提高SfM算法中匹配效率。然而，基于成本、風險等原因，低空無人機通常不搭載高精度的POS設備，直接采用記錄的GPS/IMU數據作為外方位元素初值參與光束法區域網平差會給三維重建結果帶來明顯的系統誤差[13]，因此，影像外方位元素全局一致性初值仍需其他算法來準確解算。文獻[7]采用增量式SfM算法進行低空攝影測量數據處理，取得了與高精度POS輔助光束法平差基本相當的精度。但增量式SfM算法為避免累積誤差的快速增大，在增加新的影像過程中，需經多次光束法平差迭代優化物方點和相機內、外方位元素，平差耗時隨影像數增多呈指數級增加[13]，從而制約了SfM算法在低空攝影測量數據處理效率的進一步提高。此外，增量式SfM算法依賴于初始像對選取，且僅依靠單一的匹配點數最多或關聯節點數最多為依據遍歷影像難以鎖定最佳的候選影像，以及近平面的地形物方點三維坐標解算結果可能不穩定，這些問題都將影響三維重建精度。由此可見，利用GPS/IMU數據或多次平差的傳統增量式SfM算法限制了外方位元素全局一致性全自動快速高精度解算。

在低空攝影測量外方位元素解算過程中，影像姿態求解是核心的環節，也是制約SfM算法精度和效率的主要因素之一。旋轉平均是用于解算影像全局一致性姿態參數最常用的算法[14-15]。最初，文獻[14]利用奇異值分解和最小二乘解算出全局一致性四元數形式的旋轉矩陣，在相對旋轉估計無粗差的理想情況下，這些算法能獲得高精度的旋轉相機旋轉矩陣。然而，基于影像間匹配點估計相對旋轉矩陣，由于匹配點數量、質量及分布情況等導致相對旋轉矩陣解算不可避免地存在粗差[9]。針對這一問題，相應的改進算法也被提出，具有代表性的有利用半定松弛算法削弱粗差的全局運動估計[16]、利用迭代特征向量法剔除外點[17]，引入李代數進行線性化旋轉平均迭代剔除粗差[9,15]。這些方法雖能在一定程度上剔除粗差和提高旋轉平均計算效率，但局限于減小最小二乘旋轉平均全局優化中的粗差影響，在旋轉矩陣初值的確定過程中未有類似增量式SfM的平差優化過程。因此，全局影像旋轉矩陣初值可能存在較大的累積誤差，而初值的好壞影響到全局平差優化的迭代收斂效率和最終的平差精度[18-19]。特別是飛行不穩定的輕小型無人機平臺易造成相機姿態角變化大，若旋轉與平移矩陣初值未被準確解算可能造成平差優化迭代不收斂。

針對上述問題，本文顧及旋轉矩陣初值確定，旨在構建適用于低空無人機平臺攝影測量三維重建方法，提出一種耦合單-多旋轉平均迭代優化的低空影像SfM三維重建方法，以匹配點數、關聯節點數等多因素構建最優增量決策函數，利用顧及粗差的單旋轉平均(single rotation averaging,SRA)增量方式添加立體模型，兼顧多旋轉平均(multiple rotation averaging,MRA)自適應迭代優化旋轉矩陣，最后利用光束法區域網平差統一優化整個網絡，得到精確的物方點、影像旋轉與平移矩陣。

1 耦合單-多旋轉平均的SfM算法

1.1 增量式SfM

SfM算法的核心在于通過特征匹配得到關聯重疊影像之間的同名點，以最小化特征點的重投影誤差來精確求解相機內外方位元素與物方點三維坐標的最大似然估計[7]。在計算機視覺中，三維物方點與二維平面點映射關系可由投影變換表示為

x=PX

(1)

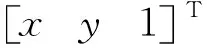
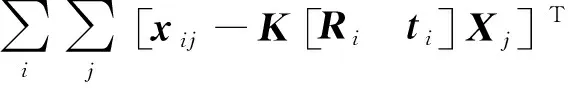
(2)

式中，Xj為待求的第j個物方點；xij為Xj對應在影像i上的已知坐標。

當前，增量式SfM是低空攝影測量數據處理中通常采用的方法[7]。在增量式SfM中，首先需要選取兩個初始立體像對構建初始局部坐標系。通常選擇足夠多同名點和多度重疊的像對作為初始像對，但若選擇的像對是近平面的地形，解算的物方點存在不穩定性。而且，增量式SfM通常依靠單一的匹配點數最多或關聯節點數最多為依據遍歷所有影像和光束法循環平差迭代優化，其缺點在于隨著影像數增多平差耗時急劇增加。

針對增量式SfM方法存在的問題，全局SfM方法也被提出，用于大范圍場景重建[15]。其關鍵在于采用旋轉與平移平均算法來獲得全局一致性的旋轉與平移矩陣再進行一次光束法平差優化整個網絡。然而，全局旋轉與平移平均算法和光束法平差不同的是無須依賴三維物方點來參與平差和剔除粗差點，而是基于影像幾何圖與相對定向關系，通過最小二乘迭代求解最優的全局旋轉與平移參數，因此對相對定向中存在的粗差較為敏感[7,15]。

1.2 本文方法

針對增量式和全局SfM方法存在的問題并兼顧兩者的優勢，本文提出一種耦合單-多旋轉平均迭代優化方法。以增量式方法添加影像，但添加影像的局部構網平差過程并不采用光束法平差，避免因多次光束法平差造成增量式SfM方法效率低的問題。在局部構網時，為避免在物方點未參與平差而對噪聲的穩健性不強、易受粗差干擾的問題，采用局部旋轉平均對添加的影像進行平差，以緩解相對定向旋轉矩陣中粗差帶來的影響。

此外，優化初始化模型確定和影像增量添加方法，并在影像添加過程中判別已添加的影像集誤差矩陣是否超限，來進一步削弱粗差的影響，從而實現低空影像SfM快速高精度三維重建。

本文方法流程見圖1，主要思路與步驟：①構建局部參考坐標系，以基準影像對優選函數來確定初始化模型，并以其中一影像的像空間坐標系作為基準構建局部參考坐標系；②構建正置擴展樹，采用增量決策函數添加強關聯影像；③根據基于四元數與旋轉向量的單旋轉平均公式(10)和隨機采樣一致性算法(random sample consensus,RANSAC)計算各影像的像空間坐標系相對于局部參考坐標系的旋轉矩陣，并以選權迭代最小二乘法進行優化；④根據影像集Simg旋轉矩陣誤差為依據，自適應確定是否進行多旋轉平均優化，進而抑制累積誤差傳遞，并利用加權最小二乘計算平移矩陣；⑤在完成所有影像添加過程后，通過前方交會計算物方點三維坐標，采用絕對定向與光束法平差優化物方點、旋轉與平移矩陣，得到地面坐標系下的三維重建結果。

1.2.1 局部參考坐標系構建

首先，為避免窮舉匹配，利用低空攝影平臺飛控記錄的GPS/IMU數據搜索重疊影像。影像特征匹配利用基于SIFT與亞像素Harris結合的算法獲取同名點[2]，采用嚴密相對定向方法解算立體像對相對定向參數[20]，并構建關聯網絡無向圖G

G={V,E}

(3)

式中，V表示影像節點，連接邊(i,j)∈E表示影像i與j的相對定向關系。具體見圖2示例，V1、V2、V3、V4、Vi、Vj、Vn表示影像節點。

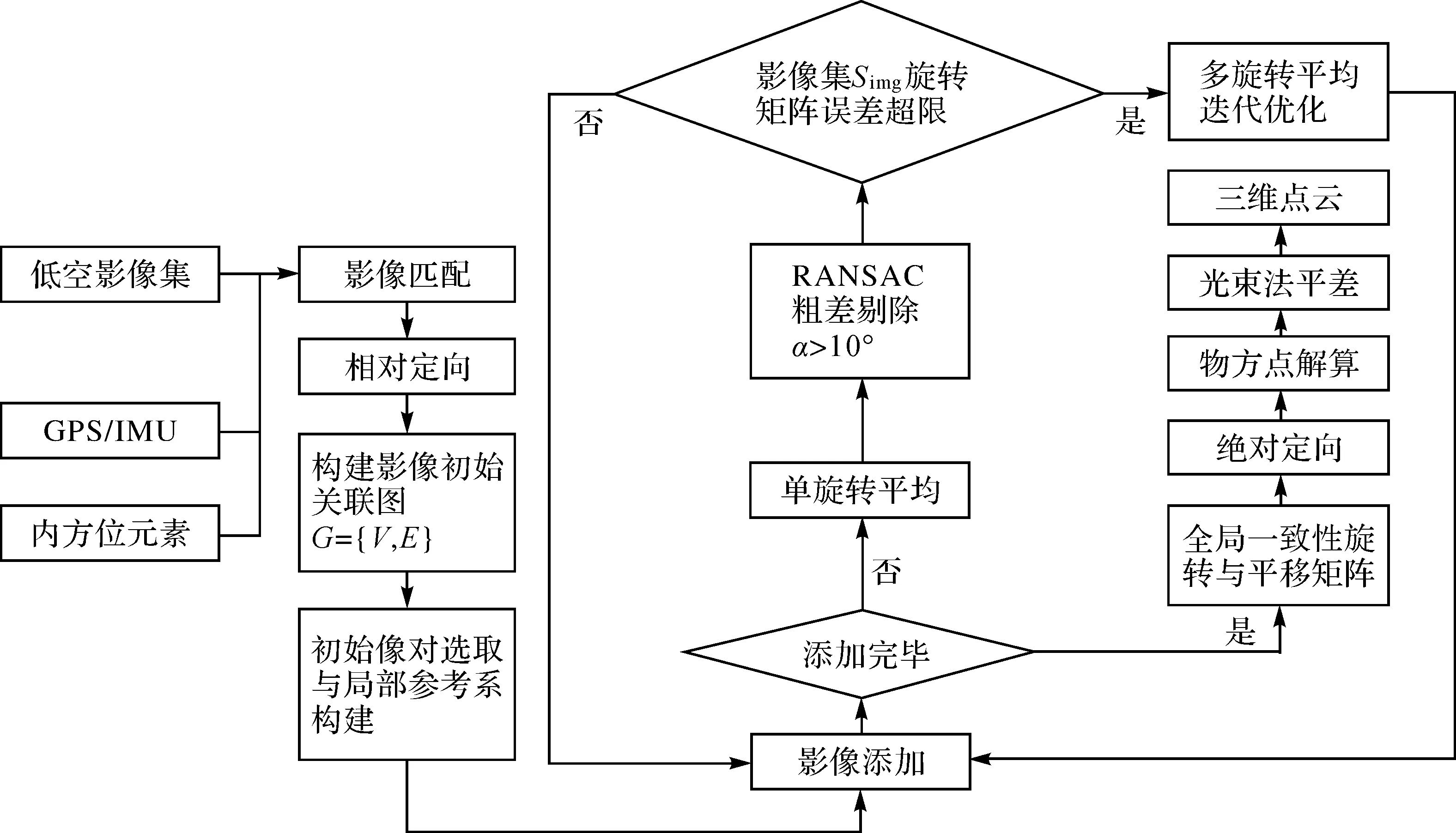
圖1 本文方法流程Fig.1 Workflow of the proposed method

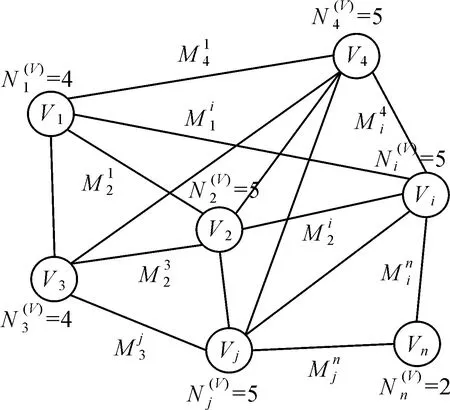
圖2 關聯網絡無向圖Fig.2 Example of undirected graph of correlated network

其次，顧及同名點數量及其分布、關聯圖連通分量、累積誤差最短傳播路徑等，綜合同名點數M、關聯節點個數N(V)、匹配點離散度D(STD)、單應矩陣估計中誤差H為依據來確定初始像對(l,r)，構建基準影像對ref優選函數

ref=argmaxf(l,r)

(4)

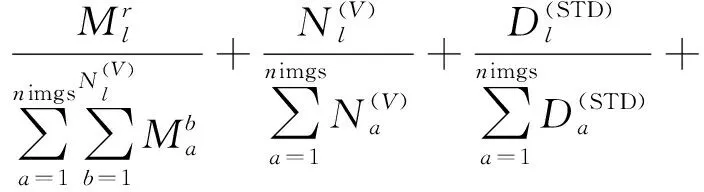
(5)

在構建局部參考系(像空間輔助坐標系)后，以增量的形式(增量決策函數值最大為依據)添加剩余影像到影像集Simg中，擴充多旋轉平均影像關聯有向圖(圖3)，采用SRA計算各影像的像空間坐標系相對于局部參考系的旋轉矩陣，并根據影像集Simg旋轉矩陣誤差是否超限來自適應進行MRA優化。圖3是圖2中影像節點在SRA與MRA結合的遍歷過程：Vi→V2→V4→Vj→V3→V1→Vn，即在確定基準影像節點Vi后，在SRA(圖3(a))，待添加的影像在①—⑥中分別為V2、V4、Vj、V3、V1、Vn，以Simg旋轉矩陣誤差是否超限來確定是否進行①—⑥各步MRA(圖3(b))優化。

1.2.2 單旋轉平均

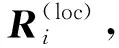
(6)

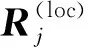
(7)

(8)

圖3 單-多旋轉平均遍歷Fig.3 Traverse images using single-multiple rotation averaging

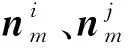
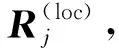
(9)

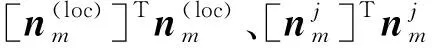
(10)

(11)

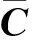
(12)

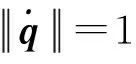
(13)

(14)

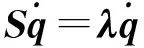
(15)

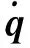
(16)

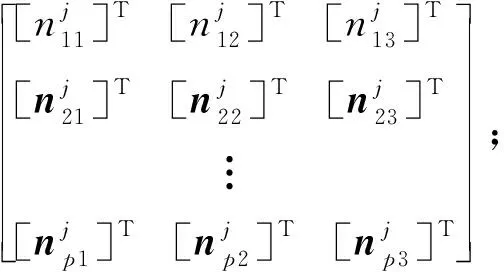
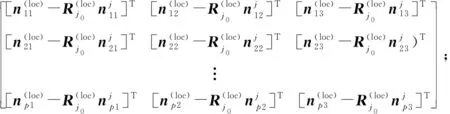
平移矩陣可由式(17)求解

(17)

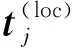
1.2.3 多旋轉平均迭代優化

本文與傳統單旋轉平均不同關鍵在于添加影像后，初值優選與局部坐標系內影像影像集Simg優化思路見圖3。在關聯圖中，旋轉矩陣計算采用正置樹結構，然后，采用選權迭代多旋轉平均自適應優化影像集Simg中的旋轉矩陣。多旋轉平均算法中，基于四元數旋轉矩陣轉換表達式為

(18)

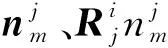
多旋轉平均中，像對(i,j)平移向量變換關系為

(19)

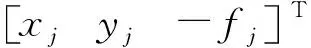
1.2.4 區域網平差與三維重建

在完成添加關聯影像到影像集Simg和解算全局一致性旋轉與平移矩陣后，利用地面控制點進行絕對定向和計算地面坐標系下的物方點坐標。然后，采用自檢校光束法區域網平差對內、外方位元素和物方點云坐標進行整體統一優化。本文以最優化恢復影像姿態與位置為主旨，添加影像過程中規避物方點參與平差運算來提高SfM效率。

2 試驗與分析

2.1 試驗數據

為驗證本文方法在多飛行平臺多地形地物環境下低空攝影測量數據處理方面的可行性、精度與效率，采用固定翼與DJI S1000+旋翼兩種飛行平臺及其搭載的兩種相機分別獲取的316幅(8條不規則航帶)與126幅影像(2條航帶)進行試驗。飛行平臺信息與相機參數見表1、表2，影像在進行空三處理前都經過了畸變差改正。試驗區包括兩個區域：①江西省上饒市尊橋鄉，包含丘陵、平原等地形，以及建筑物、道路、河流、農田、村鎮等地物，部分影像見圖4(a)；②美國西拉法葉市郊區，主要包含玉米地，部分影像見圖4(b)。

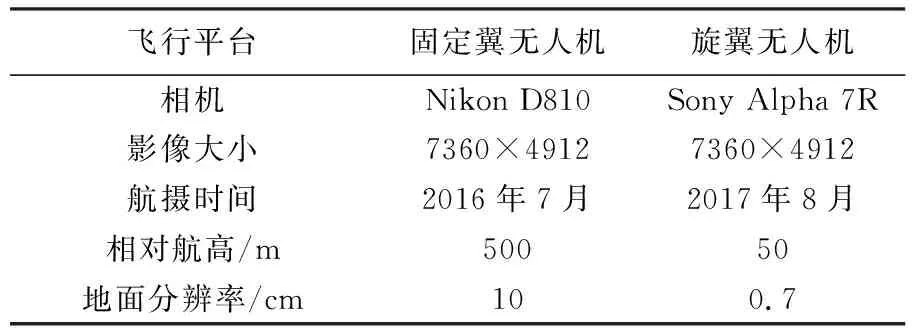
表1 無人機航攝基本情況

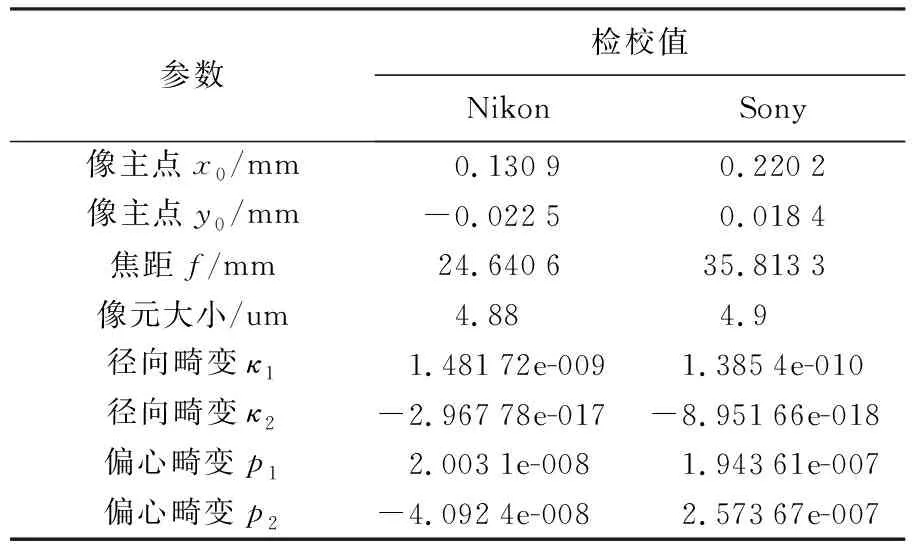
表2 相機參數

圖4 影像集部分影像Fig.4 Parts of images sets

2.2 對比試驗

同時，為便于比較分析，采用增量式單旋轉平均(Incremental)[7]、基于全局旋轉平均(Global)、基于李代數迭代選權旋轉平均方法[9,15](IRLS)、本文方法進行試驗。固定翼與旋翼無人機影像(即尊橋與西拉法葉影像)外方位元素中誤差見表3、表4。可見本文方法相對于其他3種方法能獲得精度更好的外方位元素。固定翼無人機影像中global與IRLS結果較為接近，Incremental相對最差，而表4中Global方法明顯比其他3種方法精度更低。

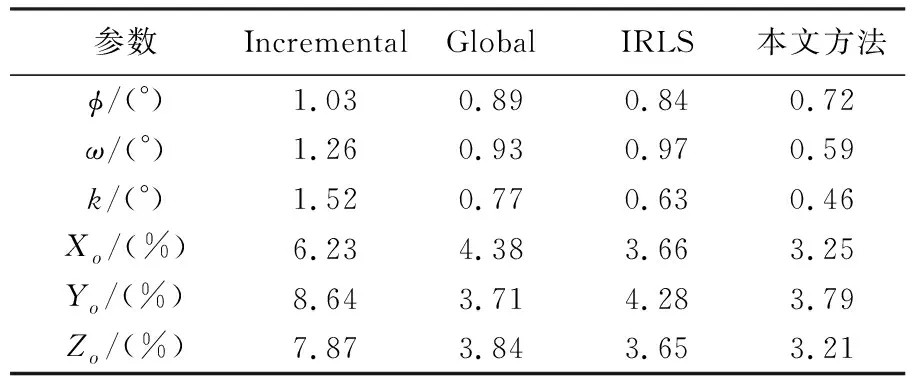
表3 尊橋影像外方位元素中誤差

在固定翼與旋翼飛行平臺試驗區域，分別采集了15個和9個地面控制點進行絕對定向，以及分別采集了12個地面控制點用于檢核，其中，西拉法葉試驗區布設了地面標識點。4種方法的檢查點殘差中誤差見表5、表6，檢查點物方殘差見圖5、圖6。尊橋影像中，本文方法檢查點平面殘差均小于0.1 m，高程中誤差約為0.13 m；西拉法葉影像中，本文方法檢查點平面與高程中誤差分別接近0.01 m、0.02 m。由圖4(a)可知，固定翼無人機平臺所攝區域紋理相對于旋翼無人機所攝區域更為豐富，圖4(b)重復紋理較多，可能存在匹配點少、分布不均勻以及匹配粗差等，導致Global方法精度明顯比其他3種方法低。

表4 西拉法葉影像外方位元素中誤差

Tab.4 RMS of exterior parameters of West Lafayette images

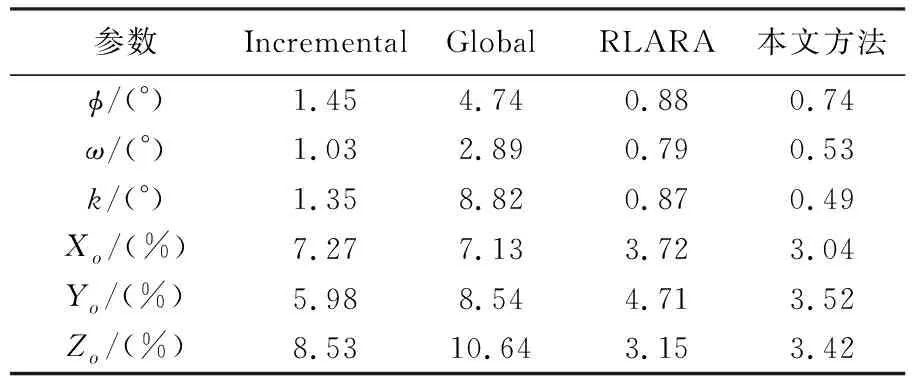
參數IncrementalGlobalRLARA本文方法?/(°)1.454.740.880.74ω/(°)1.032.890.790.53k/(°)1.358.820.870.49Xo/(%)7.277.133.723.04Yo/(%)5.988.544.713.52Zo/(%)8.5310.643.153.42

注：表中平移向量[XoYoZo]誤差根據基線歸一化的百分比表示。

表5 尊橋影像檢查點殘差中誤差

Tab.5 RMS of check points of Zunqiao images m

表6 西拉法葉影像檢查點殘差中誤差

4種方法在多視匹配得到相同的匹配點集后，通過前方交會解算物方點三維坐標，并經光束法平差和以重投影誤差大于兩個像素或3倍中誤差為約束條件來剔除粗差點，得到重建點云見圖7、圖8，本文方法獲得的三維點云明顯比其他3種方法更為密集。在尊橋影像中，本文方法可得到171 941個三維點，而Incremental法、Global法、IRLS法分別得到77 338、96 451、137 902個點；在西拉法葉影像中，本文方法可得到63 294個三維點，而Incremental法、Global法、IRLS法分別得到42 352、29 676、47 470個點。采用本文方法解算的旋轉與平移參數精度最高，重投影誤差相對較小，因而能恢復出更多的三維點。

圖5 尊橋影像檢查點物方殘差Fig.5 Residual error of check points in object space of Zunqiao images

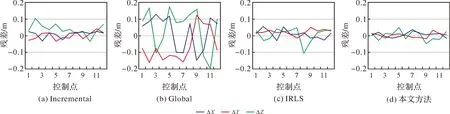
圖6 西拉法葉影像檢查點物方殘差Fig.6 Residual error of check points in object space of West Lafayette images

圖7 尊橋影像4種方法重建點云對比Fig.7 Comparison of reconstructed points cloud by four methods with Zunqiao images

圖8 西拉法葉影像4種方法DSM對比Fig.8 Comparison of reconstructed points cloud by four methods with West Lafayette images

本文主要針對SfM中全局一致性旋轉與平移矩陣的高精度快速解算展開研究。為便于比較分析，4種方法在特征提取、特征匹配階段采用同樣的方法和結果，在同一硬件條件下，運動恢復結構的耗時情況見表7所示。Incremental方法在添加新的影像時進行多次光束法平差迭代優化三維點坐標與影像內、外方位元素，平差計算隨影像數增多而不斷擴大，運動恢復結構耗時最長；Global方法因僅進行了一次全局一致性旋轉平均優化，耗時最短；IRLS與本文方法在旋轉平均過程中未有三維點云參與平差，效率也較高，且隨著影像數增多，效率提升更為顯著，但因多次旋轉平均優化導致效率比Global方法稍遜。

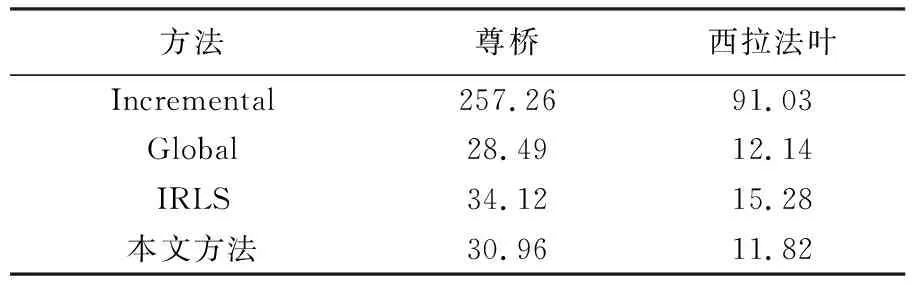
表7 運動恢復結構耗時情況

結合外方位元素中誤差、檢查點物方殘差與中誤差、運動恢復結構效率統計和數字地表模型視覺效果對比，權衡精度與效率可知，本文方法相對于Incremental、Global、IRLS 3種方法在低空影像運動恢復結構更具優勢。

3 結 論

針對SfM算法用于低空攝影測量存在初始框架構建不盡合理、影像增量決策單一、迭代優化對粗差敏感等問題，本文從初始參考系著手，構建影像增量多因素決策函數添加強關聯影像，利用四元數支持下無須物方參與平差的多旋轉平均選權迭代自適應優化獲取全局一致性旋轉與平移矩陣，從而剔除粗差和抑制累積誤差傳遞。通過固定翼與旋翼無人機影像試驗表明，得益于增量候選影像優選與外方位元素自適應優化方法，本文方法相對于傳統增量式SfM算法、全局優化、IRLS能獲得更高的成果精度，且相比傳統增量式SfM算法效率提高了8倍以上、接近全局優化方法效率，驗證了本文方法不僅適用于固定翼無人機平臺的高精度高效低空攝影測量數據處理，也適用于輕小型無人機平臺影像處理。