鋼制車輪輪輻旋壓成形數值模擬和工藝參數優化

黨斌 單穎春 劉獻棟

摘要：為指導車輪輪輻旋壓成形工藝參數的選擇，利用Simufact Forming對某款輕型客車的輪輻旋壓過程進行有限元仿真，改進旋輪軌跡的確定方法，對比厚度仿真結果和實際加工結果，驗證該仿真方法的有效性。在數值模擬的基礎上，設計四因素三水平正交試驗表，對工藝參數進行正交試驗優化設計，得到一組針對該鋼制車輪輪輻旋壓成形的最優工藝參數。利用優化后的工藝參數進行輪輻旋壓成形仿真，結果表明輪輻最大厚度偏差和最大等效應力都有所減少。

關鍵詞：鋼制車輪;輪輻;旋壓成形;旋輪軌跡;正交實驗;工藝參數;優化

中圖分類號：U463.34;TG306

文獻標志碼：B

文章編號：1006-0871（2019）01-0008-06

0 引 言

在鋼制車輪生產工藝中，輪輻旋壓成形是關鍵工序之一[1]。在輪輻的錯距強力旋壓成形過程中，加工工藝參數的選擇直接影響產品質量和生產效率。單純依靠“試錯法”研究輪輻錯距強力旋壓工藝，使產品達到預期目標，成本高且生產周期長。

隨著計算機技術的發展和有限元法理論的進步，基于有限元法的計算機軟件逐漸應用到鋼制車輪輪輻生產和研發過程中。利用金屬成形工藝模擬平臺Simufact Forming可模擬輪輻旋壓成形過程，獲得工件的厚度和等效應力等物理場分布，評估成形性能，在改進工藝設計方案、提高產品質量、降低生產成本和縮短產品研發周期等方面具有巨大優勢。[2]陳茂敬等[3]針對SS400熱軋鋼板用于輪輻旋壓出現橫向開裂的現象，系統分析材料本身和旋壓工藝2方面的因素，認為導致開裂的主要原因是材料有原始裂紋和大量夾雜物以及旋壓成形比過大，但沒有研究工藝參數對輪輻成形的影響。張晉輝等[4]基于Abaqus Explicit平臺建立錐形件剪切旋壓的三維有限元模型，認為較大的旋輪進給量和芯模轉速有利于減小壁厚差，旋輪直徑對旋壓力和壁厚差的影響不顯著。陳崗等[5]基于Abaqus Explicit平臺對用于航空航天等領域的不銹鋼曲母線形件旋壓成形過程進行三維彈塑性有限元模擬研究，認為旋輪與坯料之間的間隙是決定工件壁厚均勻性的最重要因素，旋輪進給比和旋輪圓角半徑分別對工件的起皺和拉裂傾向影響最顯著。孫為朋[6]研究輪輻旋壓過程中的材料流動、板料壁厚變化、應力場和應變場等分布規律，通過試驗設計，研究不同旋輪進給軌跡、旋輪軸向錯距等參數對旋壓成形質量的影響規律，優化旋輪進給軌跡與旋輪軸向錯距的匹配。BENI等[7]建立鋁制圓板旋壓過程的有限元模型，并將仿真結果與試驗結果對比，驗證有限元模型的有效性。SANGKHARAT等[8]將正交試驗法與有限元分析相結合，研究旋輪轉速、進給率、進給深度、摩擦因數等8個參數對SPCC冷軋鋼板旋壓的旋壓力和成形質量的影響，認為支撐輪寬度對旋壓力影響較大，旋輪半徑是影響零件厚度變化的最主要因素，旋輪半徑和支撐輪寬度對零件起皺失效有較大影響。

目前，國內外對鋼制車輪輪輻的仿真較少，而鋼制車輪輪輻板厚較大，無法采用沖壓工藝加工，只能采用旋壓工藝加工，該工藝在等強度輪輻輕量化方面具有較大優勢。本文基于Simufact Forming對某型輕客車的車輪輪輻旋壓工藝進行仿真，利用正交試驗分析旋輪進給率、芯模轉速、旋輪間錯距和摩擦因數等4個參數對輪輻旋壓成形效果的影響，得到一組最優參數組合。該參數組合可使得成形效果最理想，指導實際輪輻旋壓成形過程工藝參數的調整。

1 旋壓工藝仿真方法

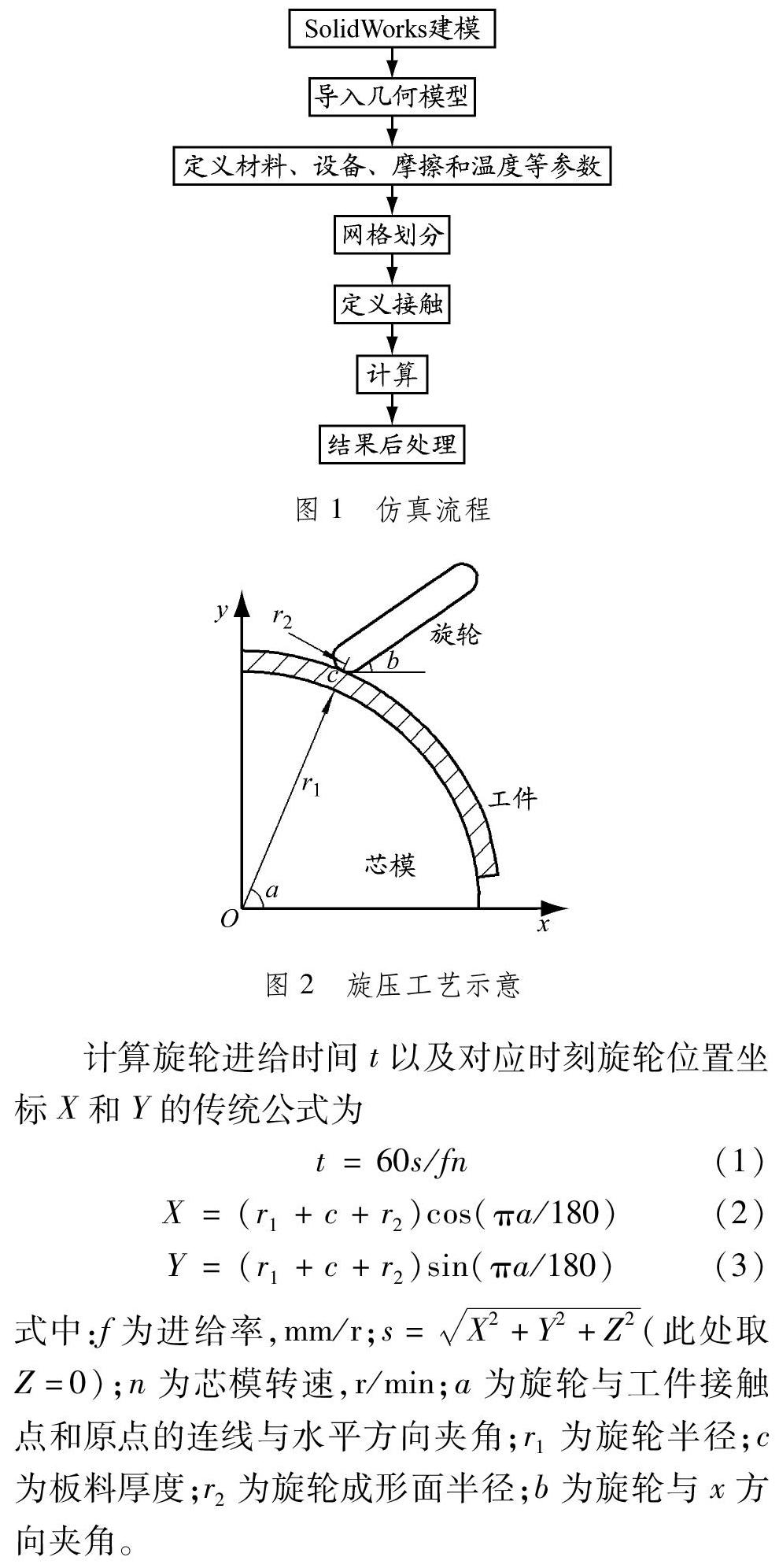
Simufact Forming對輪輻旋壓過程的仿真流程見圖1。確定旋輪軌跡是旋壓仿真的重要環節。旋壓工藝示意見圖2。

計算旋輪進給時間t以及對應時刻旋輪位置坐標X和Y

的傳統公式為

傳統旋輪軌跡確定方法具有一定的局限性，難以確定不規則形狀的軌跡和三旋輪時立體空間的旋輪軌跡。

本文采用傳統方法（式（1））確定旋輪軌跡的時間，旋輪位置坐標確定方法為：（1）在二維CAD軟件中完成零件外輪廓草圖繪制，存為IGES格式;（2）將IGES文件導入HyperMesh中進行線網格劃分，導出為MARC格式文件，見圖3;（3）在Excel中對MARC文件進行整理即可得到旋輪軌跡坐標，見圖4;（4）將整理后的旋輪軌跡導入Simufact Forming中。與傳統幾何方法相比，此方法可以適用于任何形狀、任何空間位置的旋輪軌跡的確定。

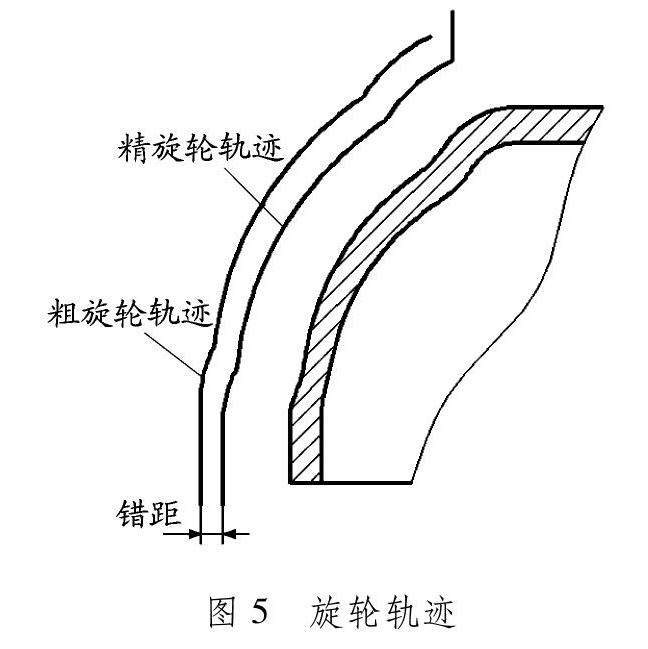
控制2個旋輪的運動軌跡實現鋼制車輪輪輻的成形，見圖5。利用上述軌跡確定方法確定旋輪軌跡，其中軟件定義的軌跡為旋輪成形面圓心的軌跡。

毛坯與尾頂間設置為固定連接，毛坯與芯模、毛坯與2個旋輪之間設置為接觸;芯模與尾頂同步主動旋轉，2個旋輪在接觸面摩擦力的作用下被動旋轉，同時分別沿各自軌跡做平移運動。旋壓成形工藝的三維仿真模型見圖6。板料各項材料參數對成形結果至關重要。該模型板料初始厚度為8.0 mm，其彈性模量為190 GPa，泊松比為0.3，密度為7 800 kg/m3，所對應的塑性部分應力-應變參數見表1。根據相關企業的實際加工經驗，初步選定一組輪輻旋壓參數：旋輪進給率為2.0 mm/r，芯模轉速為200 r/min，2個旋輪間錯距為5.0 mm，旋輪與板料間摩擦因數為0.13。仿真停止時間與精旋輪進給時間一致。

2 旋壓仿真結果分析

當旋壓成形工藝仿真計算完成后，查看板料厚度云圖和仿真剖面，見圖7和8。實際加工輪輻剖面見圖9。在輪輻剖面上選取11個測點（見圖10）測量其厚度，比較各點實測厚度與對應的仿真厚度，結果見表2和圖11。由此表明，測點1、2、3和11的仿真結果較實際結果偏薄，最大偏差不超過5.08%;測點4仿真結果與實際結果吻合較好;測點5～10的仿真結果較實際結果偏厚，最大偏差不超過12.43%。因此，所采用的仿真方法可較準確地預測輪輻截面厚度。

3 基于正交試驗設計的輪輻旋壓工藝參數優化

正交試驗設計是研究多因素、多水平的一種試驗設計方法。根據正交性，從全面試驗中挑選出部分有代表性的點進行試驗。這些有代表性的點具有均勻分散、齊整可比的特點，可以實現以最少的試驗次數達到與大量全面試驗等效的結果，因此正交表設計試驗是一種高效、快速而經濟的多因素試驗設計方法。[9]

上述仿真結果中輪輻截面厚度與實測厚度的變化規律基本一致，為使仿真成形后輪輻各截面厚度更接近實測結果、減少廢品率，選取最大厚度偏差和最大等效應力作為正交優化目標;根據實際加工經驗，選取對輪輻旋壓成形影響較大的4個因素作為正交試驗的4個影響因子[10]，每個因素選取3個水平，設計四因素三水平的正交試驗表L9（34）。按照正交試驗表試驗順序進行9組仿真分析，獲得車輪輪輻最大厚度偏差以及輪輻中的最大等效應力，見表3。表3中：A為旋輪進給率、B為芯模轉速、C為錯距、D為摩擦因數。

為更直觀地分析各因素對輪輻旋壓結果的影響，根據表4和5中的均值繪制各因素水平影響的趨勢，見圖12和13，其中：橫坐標中A、B、C、D分別表示進給率、芯模轉速、錯距和摩擦因數，下標數字1、2、3分別表示各因素對應的轉速為160、180和200 r/min，例如B1表示芯模轉速160 r/min。

由表5和圖12可以看出，最大厚度極差的大小排列順序為D>B>C>A，即摩擦因數>芯模轉速>錯距>進給率，說明摩擦因數對最大厚度偏差

的影響最大，進給率對最大厚度偏差的影響最小。由于最大厚度偏差越小越好，因此按最大厚度最優取得的工藝參數組合為A2B1C3D1;從表5和圖13可以看出，最大等效應力極差的大小排列順序為C>D>B>A，即錯距>摩擦因數>芯模轉速>進給率，說明錯距對最大等效應力的影響最大，進給率對最大等效應力的影響最小。由于最大等效應力越小越好，因此按最大等效應力最優取得的工藝參數組合為A3B3C1D2。

由上述分析可知，最大厚度偏差和最大等效應力2個指標達到最優時所選的工藝參數組合不一致，因此需要采用綜合平衡法確定最優工藝參數組合。綜合平衡分析結果見表6～9。

由表7可知：取A2時的最大厚度偏差比取A3時減小4.35%（有利），而最大等效應力只增加1.17%（不利）;取A3時的最大厚度偏差比取A2時增加4.17%（不利），而最大等效應力只減少1.18%（有利）。因此，進給率取A2。同理，芯模轉速取B1，錯距取C1，摩擦因數取D1。

通過以上分析，最優工藝參數組合為A2B1C1D1，即進給率為1.5 mm/r，芯模轉速為160 r/min，錯距為5.0 mm，摩擦因數為0.13。由于最優參數組合不在正交試驗表的9組試驗之中，因此采用優化參數組合進行有限元仿真分析，實際厚度與優化后仿真厚度對比見表10，優化后的最大等效應力見圖14。

由表10可以看出：最大厚度偏差出現在測點10位置，其值為10.68%，小于前面9組仿真中最大厚度偏差最小值12.43%。由圖14可知：最大等效應力為636.92 MPa，小于前面9組仿真中最大等效應力最小值644.90 MPa，證明參數組合優化有效。

4 結 論

基于Simufact Forming，改進旋輪軌跡確定方法，使其更具通用性。借助正交試驗優化方法，選取進給率、芯模轉速、錯距和摩擦因數等4個參數，針對輪輻成形后的最大厚度偏差和最大等效應力進行優化，得到一組最優加工參數組合，有效減小最大厚度偏差、降低最大等效應力，對產品實際加工有一定的指導意義。

（1）采用本文優化的旋輪軌跡確定方法，對輪輻旋壓加工過程進行仿真模擬，仿真厚度與實際厚度的變化規律一致，驗證旋輪軌跡確定方法和旋壓仿真方法的有效性。

（2）通過正交試驗，分析進給率、芯模轉速、錯距和摩擦因數對旋壓仿真結果的影響，結果表明：摩擦因數對最大厚度偏差影響最大，而且隨著摩擦因數的增加，最大厚度偏差有增大的趨勢;進給率對最大厚度偏差的影響最小;影響最大等效應力的2個主要因素是錯距和摩擦因數，其次是芯模轉速和進給率。

（3）通過正交試驗優化設計，獲得一組優化工藝參數組合：進給率為1.5 mm/r，芯模轉速為160 r/min，錯距為5.0 mm，摩擦因數為0.13。采用該組工藝參數，可將最大厚度偏差降為10.68%，為該款車輪輪輻旋壓工藝參數的選擇提供參考。

參考文獻：

[1] 陸培明， 錢春華， 童恬. 汽車鋼制車輪行業的現狀和趨勢[J]. 汽車工程， 2006， 28（5）：504-507.

[2] 張云開. 鋼制車輪輪輞滾壓和輪輻強力旋壓成形工藝分析研究[D]. 泉州：華僑大學， 2014.

[3] 陳茂敬， 呂學星， 谷國華. SS400旋壓輪輻開裂原因分析[J]. 山東冶金， 2007， 29（S1）：78-79. DOI：10.16727/j.cnki.issn1004-4620.2007.s1.011.

[4] 張晉輝， 詹梅， 楊合， 等. 工藝參數對剪切旋壓旋壓力和壁厚差的影響[J]. 材料科學與工藝， 2007， 15（2）：182-185. DOI：10.3969/j.issn.1005-0299.2007.02.009.

[5] 陳崗， 詹梅， 楊合， 等. 基于正交優化的異型薄壁殼體強力旋壓成形有限元分析[J]. 塑性工程學報， 2008， 15（4）：67-71.

[6] 孫為朋. 鋼制車輪疲勞性能分析及輪輻旋壓成形工藝參數研究[D]. 濟南：山東大學， 2016.

[7] BENI H R， BENI Y T， BIGLARI F R. An experimental-numerical investigation of a metal spinning process[J]. Proceedings - Institution of Mechanical Engineers：Part C：Journal of Mechanical Engineering Science， 2010， 203：509-519. DOI：10.1243/09544062jmes2133.

[8] SANGKHARAT T， DECHJARERN S. Spinning process design using finite element analysis and TAGUCHI method[J]. Procedia Engineering， 2017， 207：1713-1718. DOI：10.1016/j.proeng.2017.10.927.

[9] 陳魁. 試驗設計與分析[M]. 北京：清華大學， 2015.

[10] 孫騰. 基于Dynaform的鋼制車輪輪輻沖壓成形有限元模擬[J]. 裝備制造技術， 2017（5）：94-96. DOI：10.3969/j.issn.1672-545X.2017.05.030.

（編輯 武曉英）