感知旋轉(zhuǎn)方法，感悟模型應(yīng)用

薛瓊

[摘? 要] 圖形旋轉(zhuǎn)是三大幾何變換之一，圖形旋轉(zhuǎn)的過(guò)程中蘊(yùn)含著眾多的數(shù)學(xué)規(guī)律，以圖形旋轉(zhuǎn)為依托構(gòu)建的解題方法是數(shù)學(xué)幾何重要的方法之一，文章將以一道典型問(wèn)題為例，提煉旋轉(zhuǎn)模型，探究旋轉(zhuǎn)法的解題應(yīng)用，提出相應(yīng)的教學(xué)思考，與讀者探討.

[關(guān)鍵詞] 幾何;圖形旋轉(zhuǎn);旋轉(zhuǎn)法;線段長(zhǎng);模型

典型問(wèn)題的解答

題目? 圖1所示的四邊形ABCD中，AE⊥BC，∠BAE=∠ADC，BE=CE=2，CD=5，AD=kAB （k為常數(shù)），則BD的長(zhǎng)為_(kāi)_____（用k表示）.

解答? 連接AC，由于BE=CE，AE⊥BC，故△ABC為等腰三角形，即AB=AC（等腰三角形三線合一）. 由∠ABE+∠BAE=90°，∠BAE=∠ADC，可得∠ABE+∠ADC=90°. 將△ACD繞點(diǎn)A順時(shí)針旋轉(zhuǎn)至點(diǎn)C與點(diǎn)B相重合，再連接DF，如圖2所示，進(jìn)而可證△ADC≌△AFB，由全等性質(zhì)得∠AFB=∠ADC，BF=CD，∠BAC=∠DAF，進(jìn)一步可證△FAD∽△BAC，所以∠AFD=∠ABC，∠BFD=90°. 由AD=kAB可得DF=kBC=4k，在Rt△BDF中由勾股定理可得BD2=BF2+DF2，因此BD=.

解題模型的提煉

上述考題在求解過(guò)程中采用了圖形旋轉(zhuǎn)的方式，將△ACD繞點(diǎn)A順時(shí)針旋轉(zhuǎn)了一定的角度，使得AC與AB邊相重合，使兩個(gè)不相鄰的角結(jié)合在一起，且獲得Rt△BFD，其中的直角∠BFD在整個(gè)解題中起著重要的作用，是構(gòu)建代數(shù)方程的關(guān)鍵. 上述解題過(guò)程利用到了幾何內(nèi)容最為重要的一種模型——旋轉(zhuǎn)模型，旋轉(zhuǎn)模型對(duì)于構(gòu)建等角、等邊、圖形相似與全等有著重要的意義，而這些條件是后續(xù)解題突破的基礎(chǔ)，下面將深入探析幾何的旋轉(zhuǎn)模型.

旋轉(zhuǎn)模型用到的基本理論是幾何旋轉(zhuǎn)的性質(zhì)，在圖形旋轉(zhuǎn)過(guò)程中圖形的形狀不變、圖形全等、對(duì)應(yīng)邊、對(duì)應(yīng)角相等，且對(duì)應(yīng)點(diǎn)到旋轉(zhuǎn)中心的距離相等，邊的旋轉(zhuǎn)角度也相等.

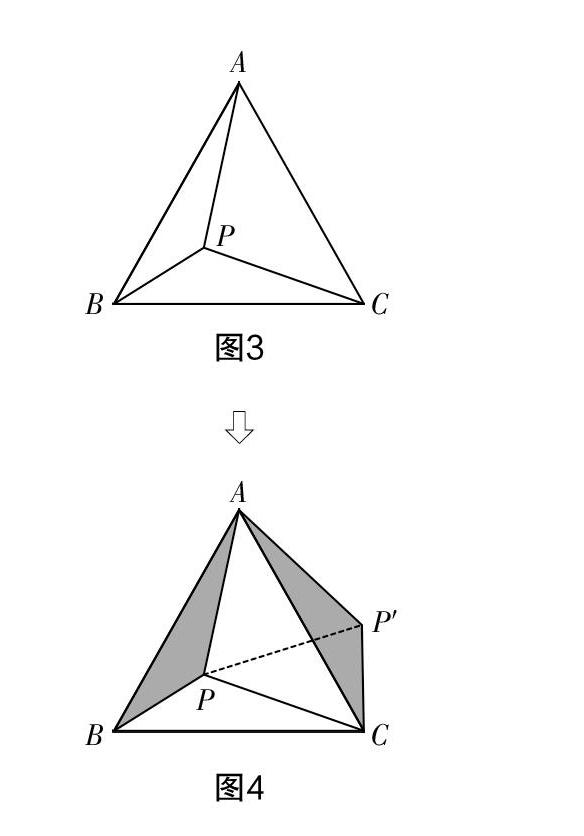
上述考題是關(guān)于基本三角形的旋轉(zhuǎn)，以圖3所示的△ABC為例，在圖形旋轉(zhuǎn)過(guò)程中必須明確旋轉(zhuǎn)的三要素——旋轉(zhuǎn)中心、旋轉(zhuǎn)方向和旋轉(zhuǎn)角度. 在等邊三角形ABC的內(nèi)部存在一點(diǎn)P，將△ABP繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)∠BAC，則AB將與AC相重合，AP=AP′，AB=AC，BP=CP′，∠BAP=∠CAP′，∠ABP=∠ACP′，∠APB=∠AP′C，△ABP≌△ACP′，即兩個(gè)陰影圖形全等，對(duì)應(yīng)邊和角均相等. 圖形旋轉(zhuǎn)后獲得了新的四邊形ABCP′，在該復(fù)合圖形中有一個(gè)特殊的等邊三角形△APP′（AP=AP′=PP′），出現(xiàn)了多個(gè)復(fù)合角：∠BCP′，∠BAP′，∠PCP′和∠PAP′，這些新出現(xiàn)的幾何元素可以成為問(wèn)題解答的關(guān)鍵條件.

旋轉(zhuǎn)模型的應(yīng)用

幾何旋轉(zhuǎn)法是為了解決特定的問(wèn)題，考慮到旋轉(zhuǎn)過(guò)程變化的對(duì)象較多，構(gòu)建的新模型具有多種特征，因此在使用時(shí)必須明確旋轉(zhuǎn)圖形的目的，通過(guò)旋轉(zhuǎn)可以構(gòu)建怎樣的圖形，解決哪些問(wèn)題.

通過(guò)上述旋轉(zhuǎn)模型的分析我們可以發(fā)現(xiàn)構(gòu)建了復(fù)合角，實(shí)際上是將兩個(gè)不相鄰的角緊密地聯(lián)系起來(lái)，同時(shí)也可以將不共線的線段轉(zhuǎn)換在同一直線上，即實(shí)現(xiàn)角度的“互補(bǔ)”、線段的“互補(bǔ)”. 第二種用途則是構(gòu)建特殊的圖形和幾何關(guān)系，如等邊、等腰三角形和全等、相似三角形，因此圖形的旋轉(zhuǎn)過(guò)程實(shí)際上就是線段、角度、圖形重構(gòu)的過(guò)程，旋轉(zhuǎn)模型最為普遍的用途是求解線段長(zhǎng)、幾何角度和分析圖形形狀. 利用旋轉(zhuǎn)法進(jìn)行解題時(shí)可以遵循如下思路：判斷是否旋轉(zhuǎn)→確定旋轉(zhuǎn)三要素→分析旋轉(zhuǎn)重構(gòu)條件→重組問(wèn)題條件→構(gòu)建解題思路，從而將原始條件與旋轉(zhuǎn)性質(zhì)條件充分結(jié)合起來(lái)，為后續(xù)的解題突破提供幫助. 下面結(jié)合一道考題深入講解旋轉(zhuǎn)模型的利用.

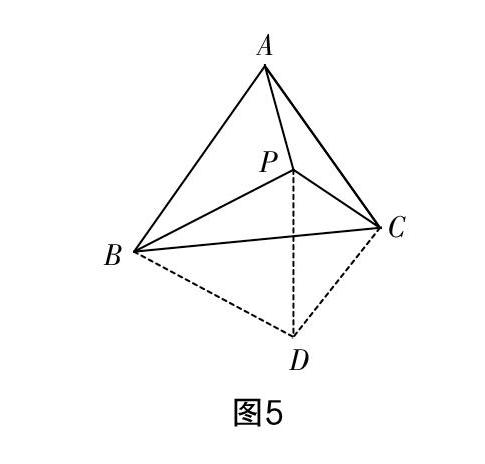
例1? 圖5所示等邊△ABC的內(nèi)部有一點(diǎn)P，已知∠APB，∠BPC和∠CPA的大小之比為5 ∶ 6 ∶ 7，則以線段長(zhǎng)PA，PB和PC三邊組成的三角形的內(nèi)角大小之比為_(kāi)_______（由小到大）.

分析：

第一步：判斷是否旋轉(zhuǎn).

由問(wèn)題出發(fā)進(jìn)行分析，要求解△ABC內(nèi)部三條線段所構(gòu)三角形的內(nèi)角之比，考慮到三條線段沒(méi)有形成閉合圖形，顯然需要通過(guò)旋轉(zhuǎn)的方式將其連接成三角形.

第二步：確定旋轉(zhuǎn)三要素.

將△ABP以點(diǎn)B為旋轉(zhuǎn)中心，順時(shí)針旋轉(zhuǎn)60°得到了△CBD，連接PD，如圖5所示.

第三步：分析旋轉(zhuǎn)重構(gòu)條件.

由于△ABP通過(guò)旋轉(zhuǎn)得到了△CBD，旋轉(zhuǎn)前后AB=BC，BP=BD，AP=CD，∠BDC=∠BPA.

第四步：重組問(wèn)題條件.

結(jié)合∠BPD=60°可得△PBD為等邊三角形，有PD=PB，則以線段PC，PD和CD為三邊的△PCD就是題干要求組成的三角形，求三角形內(nèi)角大小之比就是求∠PDC，∠CPD和∠PCD的大小之比.

第五步：構(gòu)建解題思路.

根據(jù)條件“∠APB，∠BPC和∠CPA的大小之比為5 ∶ 6 ∶ 7”可得∠APB=100°，∠BOC=120°，∠CPA=140°，則∠PDC=∠BDC-∠BDP=40°，∠CPD=∠BPC-∠BPD=60°，進(jìn)而求得∠PCD=80°，所以∠PDC，∠CPD和∠PCD的大小之比為2 ∶ 3 ∶ 4，即以PA，PB和PC三邊組成的三角形的內(nèi)角大小之比為2 ∶ 3 ∶ 4.

旋轉(zhuǎn)模型的拓展

從上述考題的分析可知旋轉(zhuǎn)模型可以用于三角形類型題中的邊長(zhǎng)和角度分析，對(duì)于其他多邊形我們也可以采用旋轉(zhuǎn)的方式來(lái)構(gòu)建解題模型，求解一些較為特殊的問(wèn)題，如求解面積、關(guān)系式證明等. 下面我們以正方形題型為例進(jìn)一步探究旋轉(zhuǎn)模型的應(yīng)用.

例2? 四邊形ABCD為正方形，點(diǎn)E是BC邊上的一點(diǎn)，AF平分∠EAD與CD相交于點(diǎn)F，試證明AE=BE+DF.

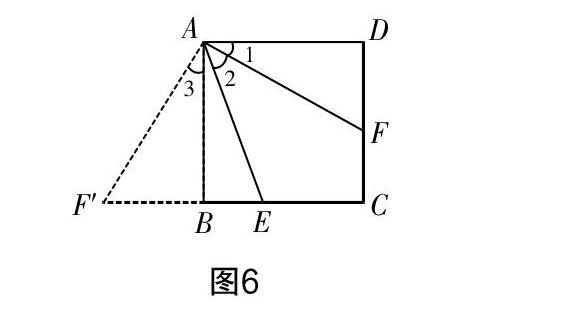
解析? 求證AE=BE+DF，考慮到三條線段長(zhǎng)分散在不同的三角形中，無(wú)法直接構(gòu)建線段長(zhǎng)關(guān)系，可以采用圖形旋轉(zhuǎn)的方式將其轉(zhuǎn)化到同一三角形中. 現(xiàn)將△ADF繞點(diǎn)A順時(shí)針旋轉(zhuǎn)90°，如圖6，則點(diǎn)D將與點(diǎn)B重合，而點(diǎn)F移動(dòng)到F′的位置. 根據(jù)旋轉(zhuǎn)模型的性質(zhì)可得△ADF≌△ABF′，進(jìn)一步可知∠AFD=∠AF′B，∠3=∠1，DF=F′B，則BE+DF=F′B+BE=F′E，只需要證明F′E與AE相等即可.

由圖6可知∠1+∠ABE+∠2=90°，因∠3=∠1，故∠3+∠ABE+∠2=90°=∠F′AE+∠2，又知∠AF′B+∠3=90°，結(jié)合∠1=∠2=∠3，可得∠AF′B+∠2=90°，即∠F′AE=∠AF′B，由等角對(duì)等邊可得F′E=AE，得證.

上述考題揭示了使用旋轉(zhuǎn)法最為關(guān)鍵的一點(diǎn)，即將不共線的線段轉(zhuǎn)移到同一直線上，進(jìn)而將旋轉(zhuǎn)模型的應(yīng)用拓展到多邊形中，不再局限于傳統(tǒng)的三角形，只需遵循圖形旋轉(zhuǎn)的三要素即可. 另外對(duì)于旋轉(zhuǎn)模型性質(zhì)的利用可以從以下兩個(gè)方面來(lái)理解：一是傳統(tǒng)意義上的旋轉(zhuǎn)前后圖形對(duì)應(yīng)元素相等，二是從圖形全等的角度，旋轉(zhuǎn)前后的兩個(gè)圖形滿足全等的條件，由圖形全等的性質(zhì)同樣可以獲得諸多旋轉(zhuǎn)性質(zhì). 因此可以將旋轉(zhuǎn)模型法拓展到所有的幾何圖形中，不受題型和旋轉(zhuǎn)圖形的限制.

方法教學(xué)的思考

1. 形成旋轉(zhuǎn)模型使用的邏輯思維

數(shù)學(xué)的解題方式有很多，考慮到圖形旋轉(zhuǎn)過(guò)程中發(fā)生位移變化的對(duì)象較多，因此使用該方法進(jìn)行解題需要嚴(yán)格遵守使用原則. 首先要根據(jù)題干的條件和問(wèn)題來(lái)判斷是否可以采用旋轉(zhuǎn)模型，然后遵循旋轉(zhuǎn)要素進(jìn)行合理旋轉(zhuǎn)，并根據(jù)旋轉(zhuǎn)模型的性質(zhì)挖掘隱含條件從而完成解題條件的重組，最后充分利用重組條件開(kāi)展解題突破. 因此進(jìn)行幾何旋轉(zhuǎn)法教學(xué)實(shí)踐時(shí)可以按照“方法判斷→實(shí)施旋轉(zhuǎn)→條件挖掘→重組條件→構(gòu)建思路”的步驟進(jìn)行，使學(xué)生形成旋轉(zhuǎn)法解題思路的深刻記憶.

2. 形成幾何旋轉(zhuǎn)法的本質(zhì)認(rèn)識(shí)

圖形旋轉(zhuǎn)前后所獲得的是全等圖形，因此可以說(shuō)利用圖形旋轉(zhuǎn)來(lái)解題實(shí)際上是對(duì)全等性質(zhì)的拓展運(yùn)用，旋轉(zhuǎn)法與圖形的全等和相似之間有著緊密的聯(lián)系，這也是教材將兩大內(nèi)容編排在一起的根本原因. 在教學(xué)圖形旋轉(zhuǎn)法時(shí)就需要引導(dǎo)學(xué)生重溫幾何全等的性質(zhì)，以及圖形旋轉(zhuǎn)過(guò)程中“變”與“不變”的性質(zhì)，從全等和不變性兩個(gè)角度引導(dǎo)學(xué)生進(jìn)行旋轉(zhuǎn)法的探索學(xué)習(xí)，充分理解該方法的理論依據(jù)，認(rèn)識(shí)旋轉(zhuǎn)模型的性質(zhì)本質(zhì)，從而深刻認(rèn)識(shí)該方法的數(shù)學(xué)內(nèi)涵.

3. 形成幾何旋轉(zhuǎn)模型的思想認(rèn)識(shí)

數(shù)學(xué)的解題方法都具有一定的理論思想，是在對(duì)應(yīng)數(shù)學(xué)思想的指導(dǎo)下構(gòu)建的解題方法，對(duì)于幾何旋轉(zhuǎn)法同樣不例外. 幾何圖形旋轉(zhuǎn)過(guò)后會(huì)得到一個(gè)全新的圖形，因此圖形旋轉(zhuǎn)的過(guò)程實(shí)際上就是數(shù)學(xué)建模的過(guò)程，圖形旋轉(zhuǎn)就是在數(shù)學(xué)模型思想指導(dǎo)下完成的. 在方法教學(xué)中不能單純地向?qū)W生傳達(dá)方法的使用步驟，還應(yīng)該依托具體的教學(xué)內(nèi)容滲透數(shù)學(xué)的模型思想，使學(xué)生體會(huì)使用數(shù)學(xué)模型解決實(shí)際問(wèn)題的優(yōu)勢(shì). 可以借助幾何畫(huà)板完成旋轉(zhuǎn)模型的構(gòu)建，使學(xué)生充分參與模型思想方法的辨析討論，提升動(dòng)手能力的同時(shí)獲得數(shù)學(xué)思想的提升.

結(jié)束語(yǔ)

從圖形旋轉(zhuǎn)法的本質(zhì)內(nèi)容來(lái)看，該方法屬于“空間與圖形”的教學(xué)范疇，因此在該方法的教學(xué)中需要遵從“觀察感知、動(dòng)手實(shí)踐、內(nèi)涵理解”的理念，即教學(xué)中要使學(xué)生掌握該方法的使用依據(jù)、具體操作和思想內(nèi)涵. 圖形旋轉(zhuǎn)的過(guò)程蘊(yùn)含著數(shù)學(xué)特有的美感，因此依托考題開(kāi)展方法教學(xué)，不僅可以使學(xué)生體會(huì)數(shù)學(xué)方法的解題魅力，還可以激發(fā)學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣，充分調(diào)動(dòng)學(xué)生的數(shù)學(xué)思維，后者對(duì)于學(xué)生的發(fā)展具有深遠(yuǎn)的意義.