高振動激發態DBr(X1Σ+，v″=8、7)與D2，Ar間的碰撞振動能量轉移

皇環環， 劉 靜， 王 倩， 李夢曉， 奧布力喀斯木·祖農， 戴 康

(新疆大學物理科學與技術學院，烏魯木齊 830046)

1 引 言

近年來，隨著受激發射泵浦技術(SEP)[1,2]、泛頻泵浦技術(OP)[3,4]、脈沖激光光解技術(PLP)[5-7]、紫外脈沖(UV)[8-10]等激光技術的的進一步發展，推動了高振動激發態分子的碰撞研究的發展.在分子的分解和重排中，高振動激發態的分子和受主分子的碰撞扮演著很重要的角色.在大氣中，因為太陽輻射、高能粒子碰撞與化學反應可以產生高振動態分子，它們對于空氣質量( 如 O3，N2O 的形成等) 有相當大的影響.在激發態分子的弛豫過程和激光誘導化學反應及燃燒等過程中，分子振動激發態的碰撞能量轉移起到重要作用，不同態之間的能量轉移速率系數可以用來預測熱傳輸和熱化率，這使得分子振動激發態的弛豫問題成為研究熱點[11-18].

Robinson等[19]發現，在HF(v)+ HF(0)→HF(v-1)+ HF(1)的振動能傳遞過程中，振動能量轉移主要發生在v=2能級，隨振動能級的增大其能量轉移率降低.Heaven等[20,21]利用受激拉曼泵浦，得到HBr(v″=1，J)振轉態，研究了其與HBr基態間的轉動能量轉移過程，實驗結果與MEG和SPEG理論研究比較，轉動能量轉移速率常數理論值與實驗值符合的比較好；利用時間分辨雙光子共振增強(REMPI)技術研究了HBr(v=1，J=0-9)和He原子的轉動馳豫速率.得到總的去布居速率常數的范圍是1.3-2.0×10-10cm3s-1，測量和計算速率常數符合良好，|ΔJ|≤3的轉移概率計算值偏低，他們對這些差異只做了初步的探討.

目前，多原子分子的復雜光譜還不能完全分辨，而雙原子分子結構相對簡單，光譜相對容易分辨，對雙原子分子振轉光譜的探測可以為氣相分子動力學研究提供寶貴的基準數據.高激發態DBr分子與其他氣體分子間的碰撞轉移，未見相關研究報道.本文研究了DBr(Χ1Σ+，v″=8、7)+ M(D2，Ar)混合系統中的碰撞弛豫過程.由激光簡并受激超拉曼泵浦[6, 22]得到DBr(Χ1Σ+，v″=8、7)激發態分子，分別測量不同氣體摩爾配比下DBr(v″=8、7)振動態的熒光光強時間演化，得到了DBr(v″=8)分別與Ar，D2的碰撞弛豫速率系數.對于DBr+ D2(Ar)混合系統，激光激發DBr(v″=8、7)，測量了v″ ≤ 8、7各振動態的時間分辨熒光信號，對單量子和二量子弛豫過程進行了討論.D2為雙原子分子其振轉能級較為豐富，在與DBr(v″=8、7)碰撞時可能發生以下近共振V-V能量轉移過程：

DBr(v″=8) +D2(v″=0) →

DBr(v″=7) +D2(v″=1)-1531cm-1

(1)

DBr(v″=8) +D2(v″=0) →

DBr(v″=6) +D2(v″=1) + 35cm-1

(2)

DBr(v″=8) +DBr(v″=0) →

DBr(v″=7) +DBr(v″=1)-326cm-1

(3)

DBr(v″=8) +DBr(v″=0) →

DBr(v″=6) +DBr(v″=2)-554cm-1

(4)

DBr(v″=7) +D2(v″=0) →

DBr(v″=6) +D2(v″=1)-1486cm-1

(5)

DBr(v″=7) +D2(v″=0) →

DBr(v″=5) +D2(v″=1) + 126cm-1

(6)

DBr(v″=7) +DBr(v″=0) →

DBr(v″=6) +DBr(v″=1)-281cm-1

(7)

DBr(v″=7) +DBr(v″=0) →

DBr(v″=5) +DBr(v″=2)-463cm-1

(8)

以上過程中，(1)式、(3)式、(5)式和(7)式對應的是單量子弛豫過程，(2)式、(4)式、(6)式和(8)式對應的是二量子弛豫過程，從能量角度看，(2)式和(6)式過程比其他近共振過程更容易發生.

對DBr+Ar的混合系統，Ar是惰性氣體原子其電子態的能級間隔較大，不會發生近共振的電子-振動能量轉移，惰性氣體Ar的充入只會加快DBr分子的單量子弛豫過程.

2 實驗方案

實驗裝置如圖1所示，圓柱形石英玻璃樣品池(直徑：25mm，長：200mm)通過真空玻璃活塞、規管接頭、四通等轉接口、針型微調閥、波紋管、卡套和法蘭與轉接系統相連.轉接系統分別連接壓強計、真空系統、DBr氣體、其他碰撞氣體(Ar/D2)和排氣系統.由于DBr氣體具有腐蝕性，轉接頭和管道均為抗腐蝕材料.由真空系統將樣品管壓強抽至10-4Pa以上，在此同時對樣品管進行加熱，樣品管外套有加熱銅套，通過熱電偶與控溫裝置連接，使得樣品池的溫度可控.將吸附在樣品池中的分子充分的排空后關閉真空系統，充入不同摩爾配比的DBr和Ar/D2混合氣體，充入氣體的壓強由壓強計測定.

YAG激光泵浦的OPO激光作為泵浦光經過反射鏡反射后，沿樣品池的軸線通過.探測激光由Ti寶石激光器提供，兩束激光小角度交叉匯聚在樣品池的中央.在匯聚點外垂直軸線方向經光纖由ICCD探測熒光.ICCD中內置單色儀和光電倍增管用來分光和放大熒光.OPO激光與ICCD間連接外觸發裝置，可控制延時.

OPO激光波長調節至743.9nm，激發混合系統中的DBr至Χ1Σ+v″=8振動態，激發態 DBr(v″=8)分子與其他氣體分子碰撞弛豫，在低于v″=8的振動態上獲得布居.調諧Ti寶石激光波長分別雙光子激發DBr分子Χ1Σ+v″=8、7、6態到第一電子激發態A1Πv′，在與激光束垂直方向探測熒光光強的時間演化，從而得到DBr分子Χ1Σ+v″=8、7、6態的布居數的時間演化，激發探測能級示意圖見圖2.與上述過程類似，將OPO激光波長調節至838.8 nm，泵浦激發DBr至Χ1Σ+v″=7振動態，由Ti寶石激光器作為探測激光器，分別激發DBr分子Χ1Σ+v″=7、6、5態到第一電子激發態A1Πv′態，探測相應的熒光光強的時間演化，從而得到DBr分子Χ1Σ+v″=7、6、5態的感應熒光光強(LIF)的時間演化曲線.

圖2 簡并受激超拉曼泵浦和檢測Fig. 2 Energy diagram for degenerate stimulated hyper-Raman pumping and probe scheme

實驗內容分3個部分：1)樣品池溫度保持在室溫(T=295 K)，在樣品池內充入不同摩爾配比的DBr和Ar(D2)的混合氣體，總氣壓保持500Pa不變.在不同摩爾配比α下，測量DBr(v″=8)振動態的時間分辨熒光強度，得到DBr分子與Ar(D2)的碰撞弛豫速率系數；2)樣品池溫度保持在室溫(T=295 K)，在樣品池內充入DBr和D2的混合氣體，摩爾配比為0.5，總氣壓為500 Pa.分別激發DBr分子到Χ1Σ+v″=8、7振動態，測量DBr分子v″≤ 8、7振動態的LIF時間演化曲線，討論是否有二量子V-V共振弛豫過程發生；3)樣品池溫度保持在室溫(T=295 K)，在樣品池內充入DBr和Ar的混合氣體，摩爾配比為0.4，總氣壓為500 Pa.激發DBr分子到Χ1Σ+v″=8振動態，測量DBr分子v″=8、7、6態的感應熒光光強的時間演化曲線，驗證單量子弛豫過程.

3 實驗結果與數據分析

3.1 振動弛豫速率系數

在樣品池內，分別充入不同摩爾配比的DBr和D2(Ar)，樣品池的總壓強約為500 Pa，在室溫(T=295 K)條件下，OPO激光激發DBr(v″=8)態，由ICCD探測DBr(v″=8)分子的時間分辨熒光.圖3(a)表示惰性氣體Ar的摩爾配比為0.4時，DBr-Ar系統中DBr(v″=8)的時間分辨LIF對數描繪，直線的斜率為DBr的v″=8能級的總弛豫率，1/τ=0.215 μs-1，相應實驗條件下DBr分子振動態v″=8的有效壽命為4.65 μs. 圖3(b)是D2的摩爾配比為0.3時，DBr- D2系統中DBr(v″=8)的時間分辨LIF對數描繪，相應實驗條件下DBr分子v″=8激發態的有效壽命為3.63 μs.

在總氣體壓強500 Pa保持不變的條件下，改變D2(Ar)在混合氣體中的摩爾配比α，用同樣的方法可以得到不同摩爾配比混合氣體中DBr的v″=8能級的總弛豫率(有效壽命).由混合氣體系統中Stern-Volmer公式可以得到DBr(v″=8)與DBr(v″=0)及Ar碰撞弛豫速率系數.混合氣體的Stern-Volmer公式如下：

(9)

式中τ為分子的有效壽命；τ0為振動激發態分子的自發輻射壽命，由于分子振動態的自發輻射很弱，因此1/τ0可近似為0；ptot為混合氣體總壓強；k為玻爾茲曼常數；T為熱力學溫度；α為Ar在混合氣體中的摩爾配比；kv″(DBr)和kv″(Ar)分別為DBr(v″=8)與DBr(v″=0)及Ar的碰撞弛豫速率系數.(9)式整理后化簡為：

(10)

圖3 最初布居在v″=8的DBr分子的時間分辨熒光光強的對數描繪. (a)DBr-Ar混合體系；(b)DBr-D2混合體系Fig. 3 Semilogarithmic plot for time-resolved fluorescence of DBr in v″=8 after preparation of v″=8. (a) DBr-Ar mixed system；(b) DBr-D2 mixed system

可以看出1/τ與混合氣體中Ar的摩爾配比成線性關系.直線的斜率表示kv″(Ar)-kv″(DBr)，截距為kv″(DBr).圖4是不同Ar氣摩爾配比下DBr分子振動態v″=8的有效壽命的Stern-Volmer描繪，樣品池溫度保持室溫(T=295 K).從圖4中直線的截距和斜率分別得到k8(DBr)為(1.33±0.4)×10-12cm3molecule-1s-1，k8(Ar)為(0.51±0.1)×10-12cm3molecule-1s-1.由于Ar是惰性氣體原子，能級間距較大，基態與第一激發態間隔81967 cm-1.在混合體系中的碰撞弛豫以DBr(v″=8)分子與DBr碰撞弛豫為主，隨著Ar在混合氣體中的摩爾配比的增加，總弛豫率逐漸降低.

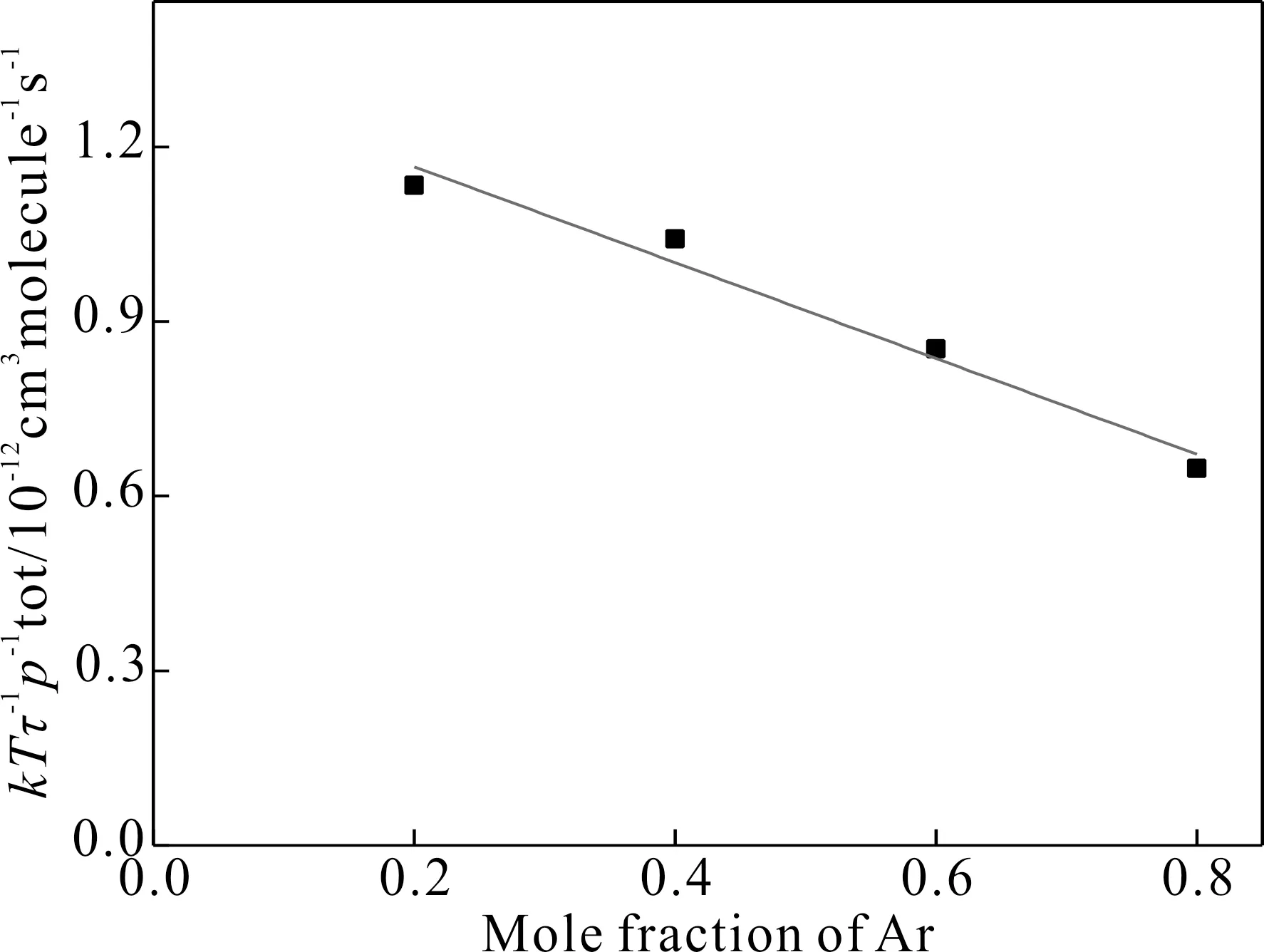
圖4 不同摩爾配比的DBr(v″=8)與Ar碰撞弛豫的Stern-Volmer描繪Fig. 4 Stern-Volmer plots for collision relaxation of different molar ratios of DBr(v″=8) and Ar

在DBr(v″=8)與D2的碰撞弛豫中，利用上面DBr(v″=8)與Ar的碰撞弛豫類似的方法，相應的描繪見圖5.由直線的截距得到DBr(v″=8)分子的自弛豫速率系數k8(DBr)為(1.08±0.4)×10-12cm3molecule-1s-1，與在DBr+Ar系統中得到的DBr分子振動態v″=8的自弛豫速率系數在誤差允許的范圍內保持一致.DBr(v″=8)分子的平均自弛豫速率系數為(1.20±0.4)×10-12cm3molecule-1s-1.由直線的斜率得到DBr(v″=8)與D2弛豫速率系數k8(D2)為 (3.5±0.8)×10-12cm3molecule-1s-1.D2為雙原子分子其振轉能級較豐富，且與DBr(v″=8)易發生近共振V-V轉移，故在DBr-D2系統中，DBr(v″=8)與D2的碰撞弛豫更強.隨著D2在混合體系中摩爾配比的增加，總弛豫率逐漸增加.

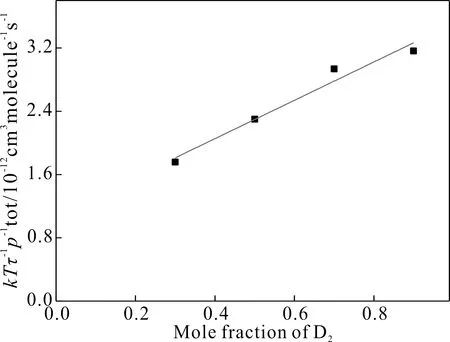
圖5 不同摩爾配比的DBr(v″=8)與D2碰撞弛豫的stern-volmer描繪Fig. 5 Stern-Volmer plots for collision relaxation of different molar ratios of DBr(v″=8) and D2

3.2 單量子和二量子振動弛豫過程

在雙原子分子和其他氣體分子混合體系中，不管雙原子分子處于低位振動態還是高位振動態，振動碰撞弛豫過程中始終存在單量子振動弛豫過程(Δv=1).對于低位振動態，單量子振動弛豫過程(Δv=1)占主導地位，碰撞弛豫速率系數隨振動激發態v″的增加而緩慢增加；對于高位振動態，由于近共振V-V能量轉移過程的存在，可能會發生Δv≥2的多量子振動弛豫過程[23]，多量子振動弛豫過程的存在使得振動碰撞弛豫速率系數會增加較快或者出現極大值[6].

對于DBr(v″=8、7)和D2系統，可能發生的近共振V-V能量轉移過程見(1)-(8)式，其中(2)式和(6)式對應的二量子弛豫近共振過程，能級差很小，只有35 cm-1和126 cm-1，從能量角度看，二量子弛豫過程容易發生.圖6(a)描述了將DBr分子布居到v″=8后，由Ti寶石激光探測v″=8、7、6振動態被激發到第一電子激發態后的感應熒光光強隨時間演化曲線.圖中正方形表示的是振動能級v″=8的布居隨時間變化的關系，圓圈表示的是振動能級v″=7布居隨時間變化的關系，三角形表示的是振動能級v″=6布居隨時間變化的關系.從圖6(a)中可以看出， DBr(v″=8)分子弛豫到v″=6振動能級上布居數的增加要快于v″=7振動能級的布居，這不可能是振動能級v″ =8經過連續的單量子弛豫躍遷到v″=6，而是越過了v″=7振動態而通過二量子弛豫直接躍遷到v″=6振動態，即振動能級v″=6的布居是由最初激發的振動能級v″ =8經過二量子弛豫過程得到的.振動能級v″=7的布居是DBr分子v″=8振動能級的單量子振動弛豫得到的.圖6(b)是DBr分子振動態最初布居在v″=7后探測v″=7、6、5處的布居數的時間演化過程.由圖6(b)同樣可以看出Δv=2的二量子弛豫發生速度比Δv= 1的單量子弛豫快.

為了證明二量子弛豫在振動能級v″=8的弛豫占主導地位，我們測量了激發DBr分子到v″=8振動能級后的v″=6態出的布居隨時間變化的關系.測量結果見圖7，在圖7中可以明顯的觀察到雙峰分布，在30 μs內出現了一個尖銳的峰，在90～150 μs的時間內出現了相對較寬的峰.第一個尖銳的峰的出現是DBr分子振動能級v″=8到v″=6的快速二量子弛豫造成的，第二個峰比第一個峰寬很多且強度較低，對應了v″=7到v″=6的單量子振動弛豫過程.

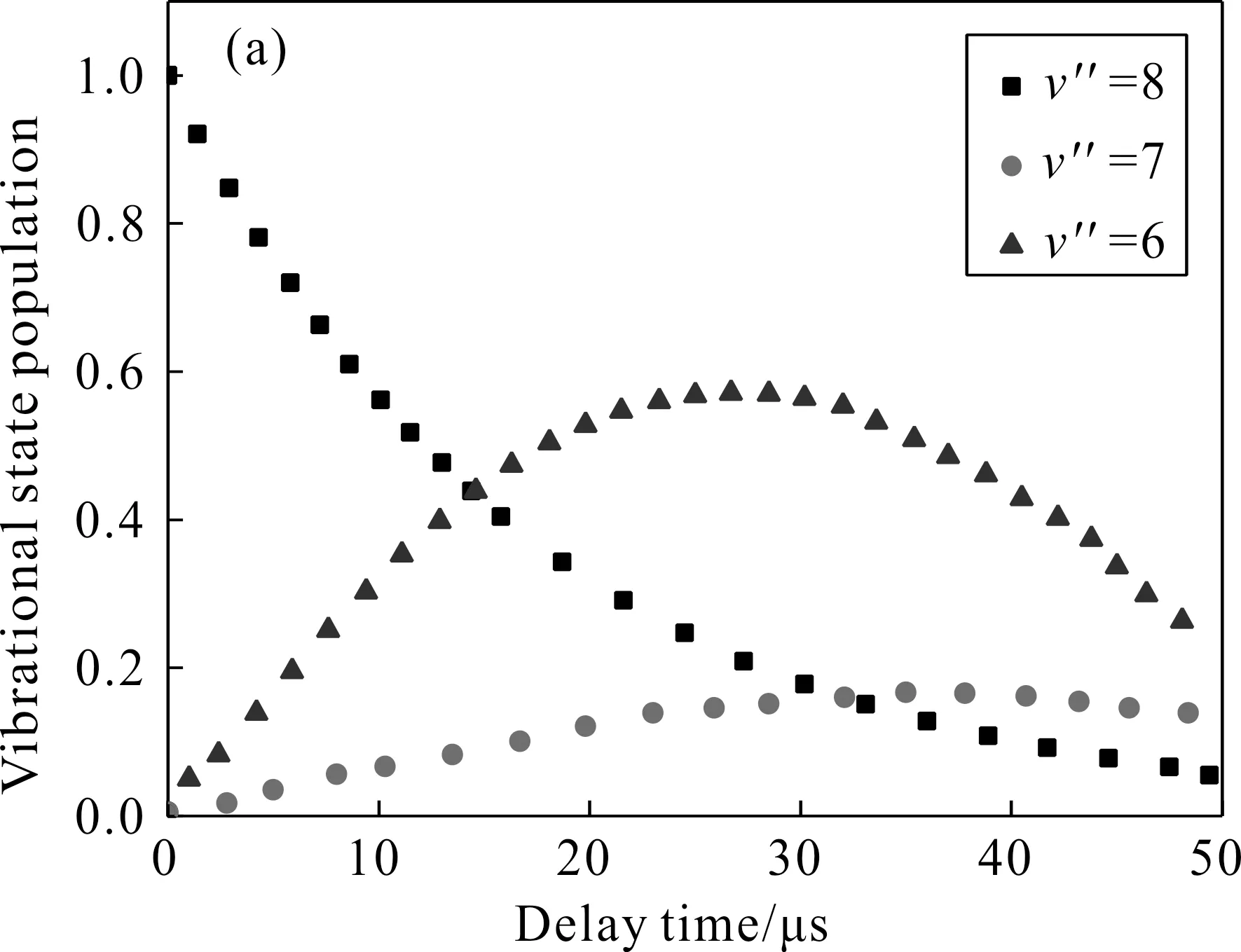
圖6 (a)最初布居到v″=8的DBr分子其v″=8、7、6振動態的感應熒光光強時間演化曲線； (b)最初布居到v″=7的DBr分子其v″=7、6、5振動態的感應熒光光強時間演化曲線Fig. 6 (a) Time-profile of the population of DBr in v″=8、7、6 after preparation of v″=8； (b) Time-profile of the population of DBr inv″=7、6、5 after preparation of v″=7

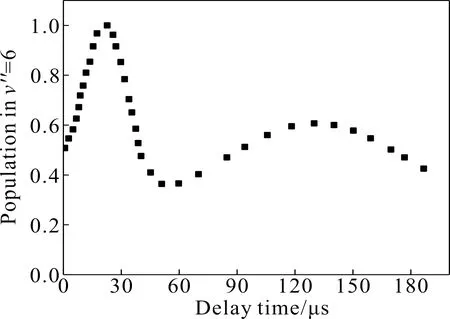
圖7 最初布居到v″=8的DBr分子其v″=6振動態的感應熒光光強時間演化曲線Fig. 7 Time-profile of the population of DBr in v″=6 after preparation of v″=8

對于DBr(v″=8)和Ar系統， 在T=295 K，總壓強約為500 Pa，摩爾配比為0.4條件下，將DBr分子激發到v″=8激發態，探測振動能級v″=8、7、6上的布居數隨時間變化關系，在圖8中呈現.如圖8所示，從圖中可以看出，DBr分子v″=7振動態上的布居速度比v″=6振動能級上的布居峰值出現在約30 μs處，是由DBr(v″=8)分子連續單量子振動弛豫(v″=8→v″=7→v″=6)造成的.在DBr(v″=8)+Ar 體系中，可能存在近共振過程(3)式和(4)式，從能量角度看，單量子弛豫過程(3)式更容易發生且Ar原子與DBr(v″=8)的猝滅碰撞加速了單量子弛豫過程的發生.

圖8 最初布居到v″=8的DBr分子其v″=8、7、6振動態的感應熒光光強時間演化曲線Fig. 8 Time-profile of the population of DBr in v″=8、7、6 after preparation of v″=8

4 結 論

本文采用簡并受激超拉曼泵浦激發DBr分子至基電子態Χ1Σ+的高振動態v″=8、7，實驗研究了DBr(v″=8、7)和D2(Ar)的碰撞弛豫過程.得到如下實驗結論：

(1)在室溫(295 K)條件下，樣品池溫度保持不變，在樣品池內充入DBr和Ar或D2的混合氣體，總氣壓保持為500 Pa.充入不同摩爾配比的Ar/D2，利用ICCD探測了不同摩爾配比下DBr(v″=8)的時間分辨熒光(LIF)，由時間分辨LIF光強的對數描繪擬合實驗數據得到各個壓強下DBr (v″=8)態的有效壽命.應用Stern-Volmer方程擬合實驗數據得到DBr(v″=8)激發態與Ar(D2)的碰撞弛豫速率系數k8(Ar)= (0.51±0.1)×10-12cm3molecule-1s-1，k8(D2)=(3.50±0.8)×10-12cm3molecule-1s-1，DBr(v″=8)的平均自弛豫速率系數k8(DBr)= (1.20±0.8)×10-12cm3molecule-1s-1.

(2)在樣品池內充入DBr和D2的混合氣體，摩爾配比為0.5，總氣壓為500 Pa.激發DBr分子到基電子態v″=8、7激發態，測量了DBr分子v″≤8、7各個振動態的感應熒光光強的時間演化曲線，結果表明在DBr(v″=8、7)和D2的混合體系中，均存在二量子近共振V-V弛豫過程.在樣品池內充入DBr和Ar的混合氣體，摩爾配比為0.4，總氣壓為500 Pa.激發DBr分子到基電子態v″=8振動態，測量了最初布居在v″=8的DBr分子振動態v″=8、7、6的感應熒光光強的時間演化曲線，結果表明在DBr(v″=8)和Ar的混合體系中，未觀察到二量子近共振弛豫過程發生，只有連續的單量子振動弛豫過程發生.