地理加權回歸模型的城市住宅價格多源熱度分析

江濟強，王斌，王明建，楊毅

(1.廣東省國土資源測繪院，廣東 廣州 510500； 2.淮海工學院測繪與海洋信息學院，江蘇 連云港 222005)

1 引 言

住宅價格問題是目前社會討論的焦點之一，研究城市區域間住宅價格分布差異很有必要。而城市不同地區住宅價格一般是分區域聚集的，說明城市住宅價格分布差異是有規律的[1]，具體來講，就是距離學校、醫院、公園、購物中心等地的距離決定了對住宅價格影響的大小[2]。隨著地理信息、互聯網等技術的進步，越來越多的分析方法相繼涌現。陳震[3]收集昆明城市各小區住宅價格，用GIS進行數據分析建模，結果表明，昆明城市住宅價格由中心向四周遞減，教育、交通、容積率等因素作為次要因素影響著住宅價格。張媛[4]通過報刊等媒介收集銀川市商品房數據，綜合GIS分析城市的交通、環境、教育、結構等都是影響城市住宅價格的因素。熊海璐，吳曉燕等[5]通過最小二乘法分析武漢住宅價格表明住宅周圍的環境和位置是決定住宅價格的最重要因素。

對于未來住宅價格的預測分析以及規律尋找，最合適的方法就是借助互聯網大數據建立回歸預測模型來進行分析預測。陳向陽、陳日新等[6]利用多元線性模型研究2003年～2010年廣州市住宅小區價格分布趨勢，發現廣州市住宅小區價格由市中心CBD向四周呈遞減趨勢，一線城市離CBD的距離是影響住宅價格的主要因素。付益松[7]通過構建南昌市2015年3月～10月的住宅價格數據庫，利用GIS克里格插值法進行分析得出影響住宅價格因子的重用大小依次為：區位、交通、公共設施、環境。

多元線性回歸模型和最小二乘法模型參數與位置弱相關，預測的精確性和可靠性較難滿足分析需求，地理加權回歸模型由于其在某些非平穩性問題研究上具有上述模型所沒有的優勢[8]，近年來得到較快發展。本文提出一種地理加權回歸模型算法，通過互聯網采集研究區內住宅小區價格及綠化率、購物中心、公園、中小學、大學、醫院等分布數據，并納入該模型中，全面分析住宅價格受綠化、交通、學校、醫院、公園等影響大小，揭示小區住宅價格的空間分異和不同因子的相關系數。

2 地理加權回歸模型(GWR)

多元線性回歸模型是用描述多個變量對一個變量產生影響的計算模型，一般難以處理變量數據實時改變的情況，主要在系統事故數值研究，系統故障提供預測以及用于海洋各成分元素研究[8]。為有效分析空間多個平穩性變量之間相互影響關系，并且有效消除非平穩性所帶來的誤差，本文采用地理加權回歸計算模型(Geographically weighted regression，GWR)，表達式為：

(1)

其中，(ui，vi)為第i個樣本點的坐標，βk(ui，vi)為第i個樣本點的第k個回歸系數，εi為第i個樣本點的隨機誤差，服從數學期望為0，方程為σ2的正態分布。不同樣本點i和j的隨機誤差相互獨立，協方差為0。即滿足：

εi∝N(0，σ2)；Cov(εi，εj)=0(i≠j)

按照加權最小二乘準則對式(1)進行最優估計，建立目標函數表達式為：

(2)

其中，wij為第i個樣本點與樣本點j之間的核函數，與距離dij相關。

(3)

(4)

利用地理加權回歸模型做出的住宅價格分析，有效考慮了影響住宅價格的眾多要素，消除了非平穩性因素的影響，若將式(1)中，βk(ui，vi)=βk(uj，vj)(i，j=1，2…n)，回歸系數不隨空間位置變化而變化，則退化為多元線性回歸模型，兩種模型比較如表1所示。

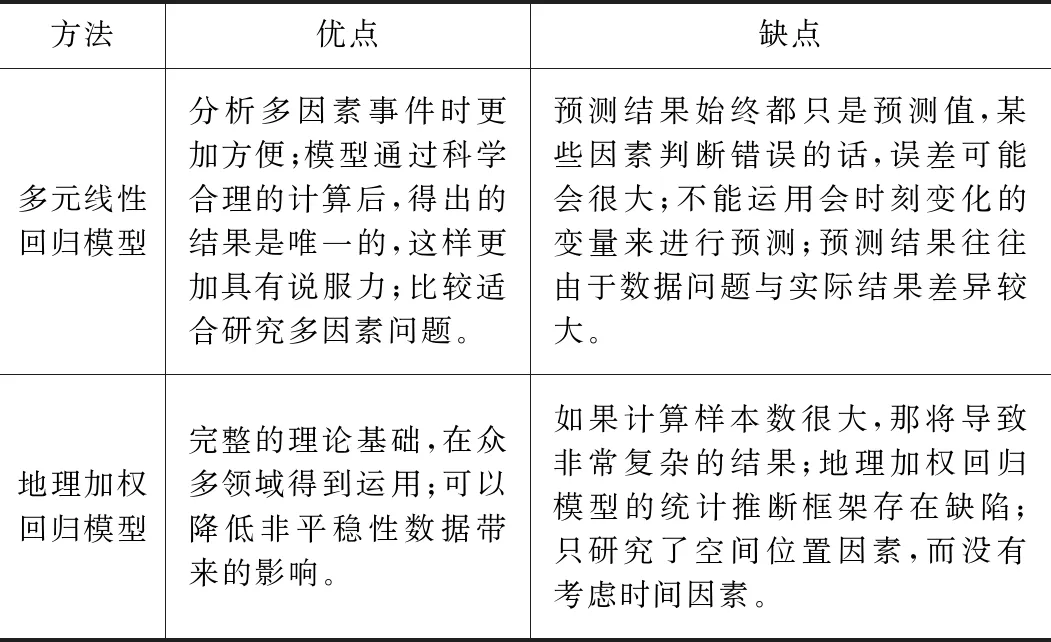
兩者模型比較 表1

3 GWR模型多源熱度分析

通過互聯網手工及自動抓取研究區住宅價格并記錄小區位置及均價，將綠化率、公園、小學等學區以及醫院、購物中心等納入主要影響因素，分析該區住宅價格高低區位變化。通過建立特征價格模型，把影響因素分為內部因素、外部因素兩大類別，內部因素研究直接可以進行建模分析，外部因素通過坐標計算距離，通過距離間的關系來研究。

Yi Yang等指出外部因素對住宅價格影響范圍研究在 1.5 km內結果最佳[8]。按照小區 1.5 km范圍內小學、中學、大學、醫院、公園、購物中心個數為依據來研究各因素對住宅價格影響大小。采集了該轄區124個小區的住宅價格和其他自變量的坐標數據，并將變量統一取對數值，如表2所示(部分數據)：

住宅銷售特征價格變量計算方法和說明 表2

3.1 數據預處理

(1)坐標轉換

由于互聯網地圖抓取的點經緯度為球坐標，為計算小區與各因子的距離，需把球坐標轉換成平面坐標，本文利用ArcGIS軟件進行坐標轉換，如表3所示(部分數據)：

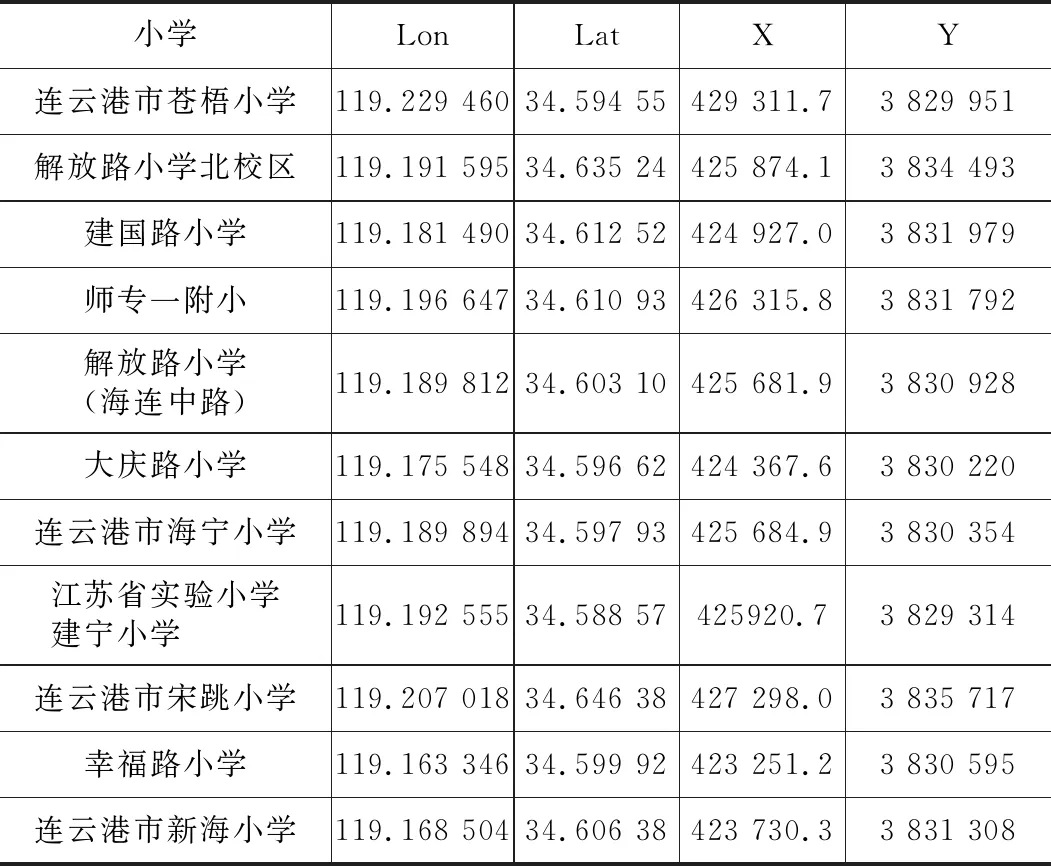
小學球面坐標轉換為平面坐標表 表3

(2)計算變量

統計小區1.5 km范圍內綠化率、小學、中學、大學、公園、醫院、購物中心數量，對各變量取ln值，如表4所示(部分數據)：

變量分布表 表4

續表4

3.2 各因子熱度分析

利用式(3)、式(4)，結合互聯網采集預處理后成果，對各影響因素進行計算并輸出制圖，如表5及圖1所示：

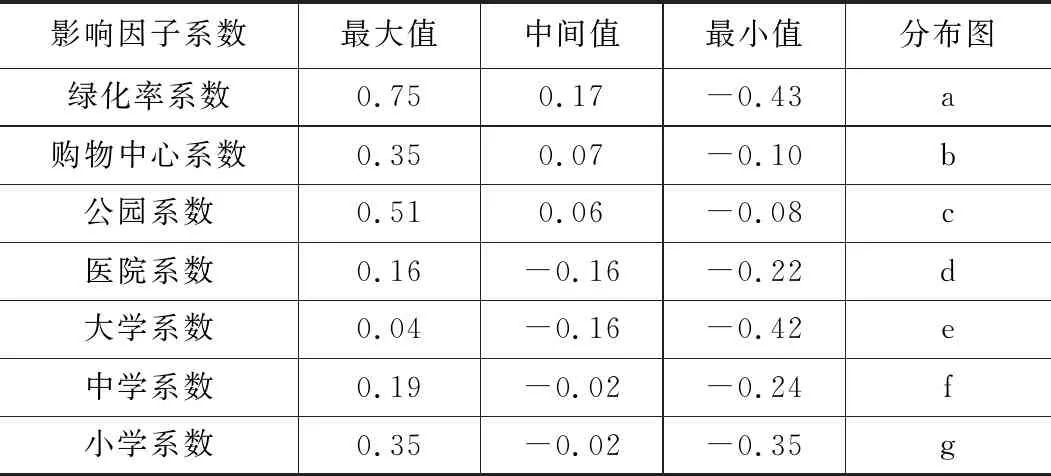
各因子熱度分析成果表 表5

總體上看，上述影響因素與住宅價格都具有相關性，但影響程度并不一致，有些甚至表現一定的負相關。在老城區，綠化率、購物中心、公園、小學與住宅價格總體呈正相關，綠化率越高、購物中心分布越廣、公園數越多，具備小學學區，小區住宅價格一般越高。其中綠化率、購物中心、公園、小學相關系數最大分別為0.75、0.35、0.51、0.35，可能原因在于老城區具有住宅密集、人流量大、活動空間緊湊、學位資源緊張等特征有關。在新城區，綠化率和住宅價格有負相關關系，說明在新城區綠化率和住宅價格沒有必然的聯系，原因可能在于新建小區環境相近且相對較好。

同時，可以看出公園對住宅價格的影響由西向東遞增，從老城區到新城區對住宅價格的影響越來越大，原因在于新城區范圍內公園數量不足造成的。醫院、大學、中學對住宅價格幾乎不產生影響，相關系數分布沒有規律可循。特別是城市周邊的小區，醫院距離對其住宅價格的影響可以忽略不計，交通便利是造成這一現象的主要原因。考慮選取樣本所在轄區高校數量較少，人數總量偏低以及中考不存在就近入讀等因素，大學、中學與周圍小區住宅價格影響極小。

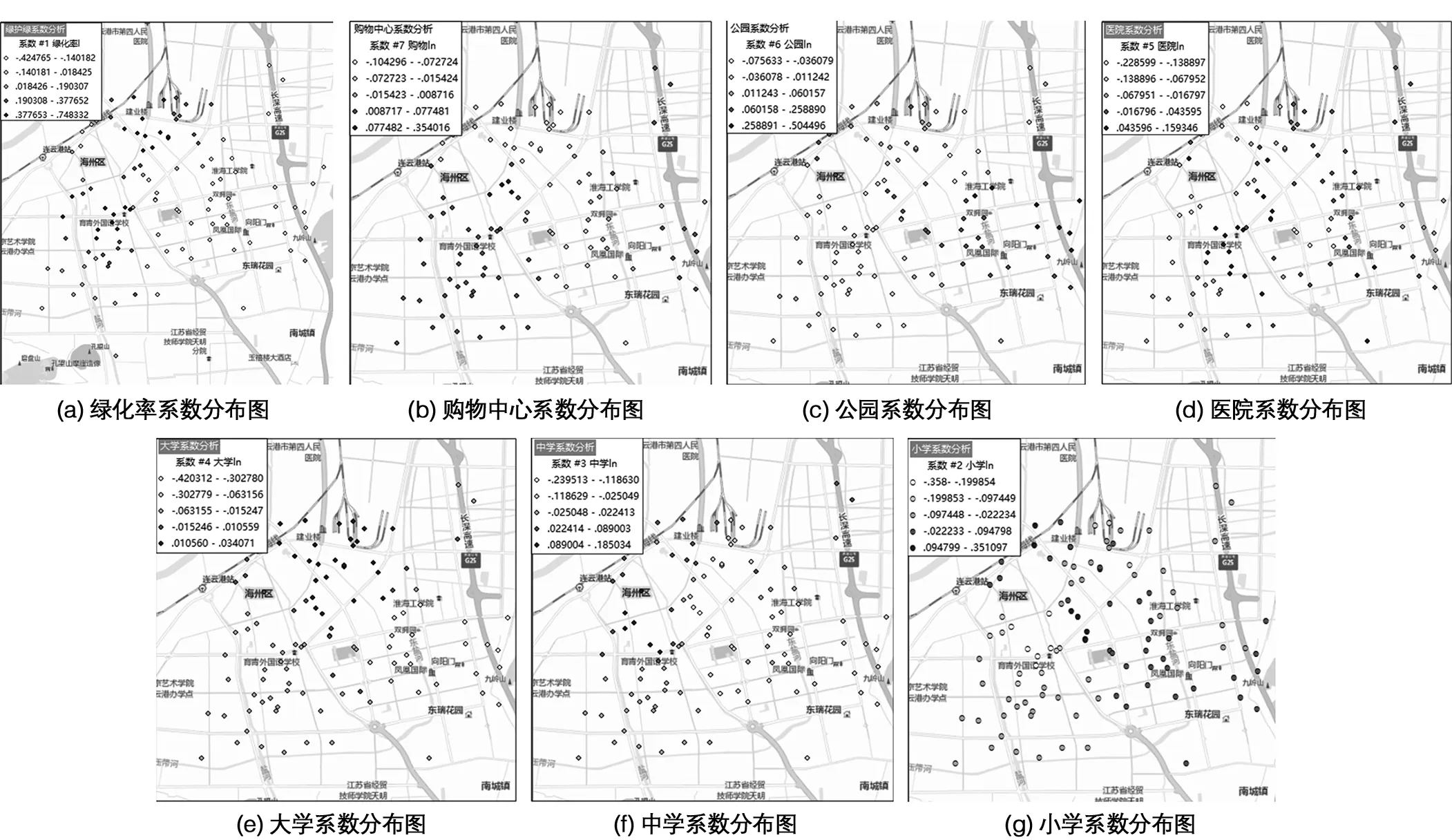
圖1城市住宅價格各因子熱度分析圖

4 結 語

本文通過采集某轄區124個小區的住宅價格數據，通過構建地理加權回歸模型，揭示小區住宅價格的空間分異和不同因子的影響，解決了回歸系數隨空間位置變化而變化的問題，但尚未解決回歸系數隨時間變化效應。目前，已有部分學者提出時空地理加權回歸模型(GTWR)，但構建最優時空帶寬及時空核函數等關鍵技術以減少模型的位置參數、降低擬合的計算量等方面，需要進一步研究。