基于LOF的K-means聚類方法及其在微震監測中的應用*
劉德彪,李夕兵,李 響,尚雪義
(中南大學 資源與安全工程學院,湖南 長沙 410083)
0 引言
微震監測技術在深部開采的礦山中,得到了越來越廣泛的應用[1-4]。微震事件數目龐大,其區域分布特征人工劃分具有較大的主觀性。聚類分析借助聚類算法實現微震事件的劃分,可降低人工劃分的主觀性,發現潛在的微震集群,從而有效的分析微震事件分布特征和活動規律。
目前,國外學者對地震事件聚類分析進行了較多研究,且在國內也越來越受到關注。Zaliapin等[5]采用K-means對人為和地質構造引起的地震事件進行了區分;Weatherill和Burton[6]采用K-means證明了震源模型可由地震目錄信息計算得到;Morales等[7]提出1種基于自適應馬氏距離的K-means聚類方法,該方法可用于球形簇和橢球形簇地震聚類;Ramdani等[8]將地震深度屬性引入到K-means聚類分析,改善了地震事件動態變化過程的圖像分辨率;吳愛祥等[9]用最短距離聚類法分析了礦山微震活動的時空分布,區分了礦山的微震聚集區;Wang等[10]采用模糊C均值聚類得出了微震事件的活動特征與三維波速之間的關系;Shang等[11]提出采用S-KL指標選擇最佳聚類數,并解釋了聚類簇與地質構造的關系;劉棟等[12-13]采用時空共享近鄰聚類算法(STSNN)和具有噪聲的基于密度的聚類方法(DBSCAN)分析了巖體的活動性。
由上述分析可知,在地震聚類分析中K-means運用最為廣泛。K-means聚類算法具有較高的計算效率和較強的靈活性,適用于球形簇結構的數據集,但數據集中的異常事件會對算法的結果產生較大的影響。初始聚類中心的選擇也容易影響聚類結果,使得聚類算法很難達到全局最優值。Wang等[14]提出了1種改進的K-means聚類算法,先用基于局部離群因子(Local Outlier Factor,LOF)的方法檢測異常并移除事件,然后用所有數據的均值作為第1個初始聚類中心,再依次計算其他的初始聚類中心,該方法提高了聚類的準確性。
本文借鑒Wang等[14]提出的算法,提出了1種新的基于LOF的K-means聚類算法(LOF-K-means),并用該方法對礦山微震事件的分布特征進行分析。首先,采用LOF檢測離群微震事件和選取初始聚類中心,再利用Krzanowski-Lai(KL)指標確定最佳聚類分組數。采用簇內誤差平方和(within-cluster Sum of Squared Errors, SSE)比較本文方法、文獻[14] K-means聚類方法和傳統K-means聚類的聚類效果。最后,采用本文方法對用沙壩礦微震事件進行聚類分析,根據聚類簇的分布特征對礦山的微震活動性作出評價。
1 局部離群因子算法
局部離群因子算法[15]是1種基于密度來進行異常事件檢測的算法。局部離群因子的大小反映對象xi對于局部中心的偏離程度,局部離群因子的值越大,說明對象xi偏離局部中心的程度越多,所在位置局部密度越小;局部離群因子的值越小,說明對象xi偏離局部中心的程度越少,所在位置局部密度越大,越接近局部中心。在本文中,用dist(xi,p)表示對象xi與對象p之間的距離,局部離群因子LOFk(xi)的具體定義如下:
定義1:對象p的第k距離k-dist(p)在數據集X中,若滿足:
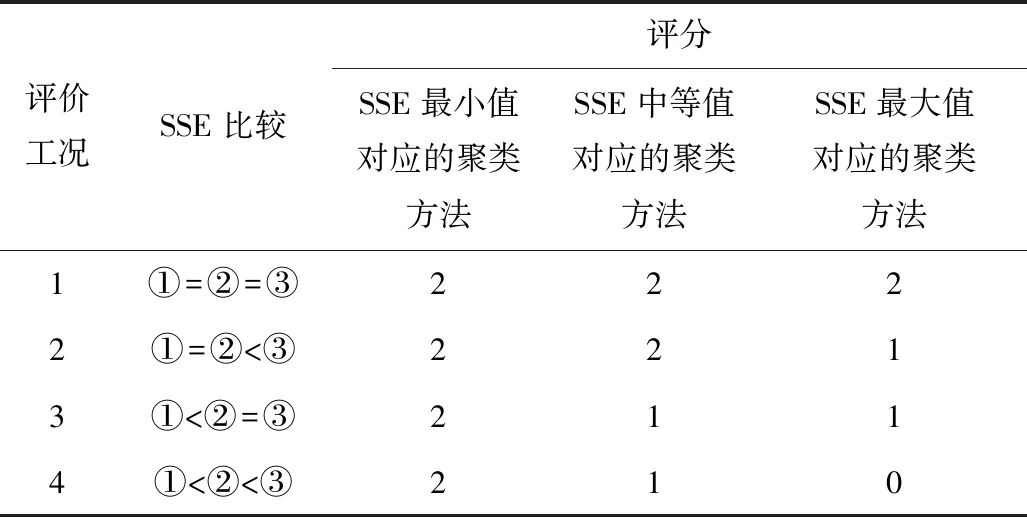
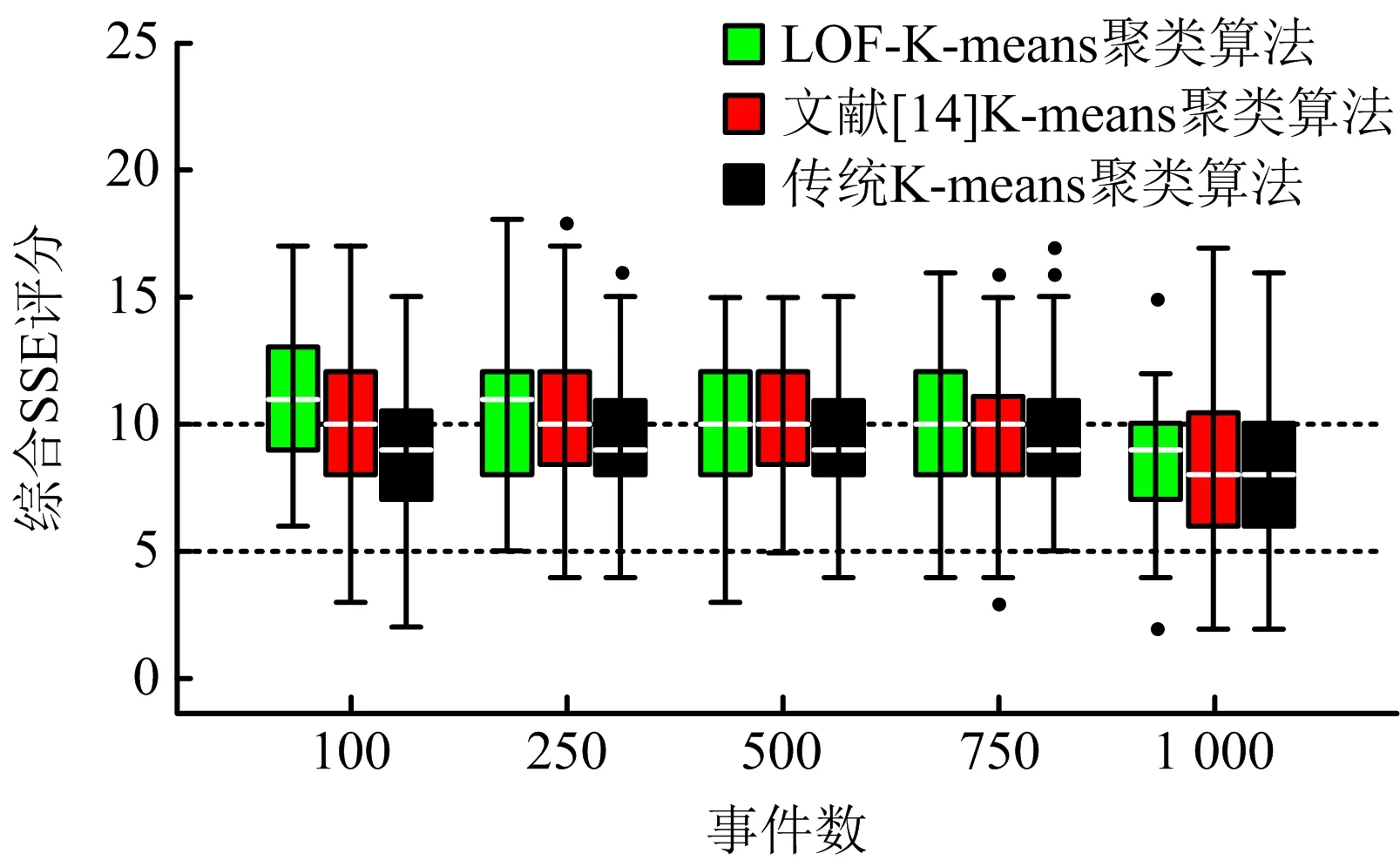
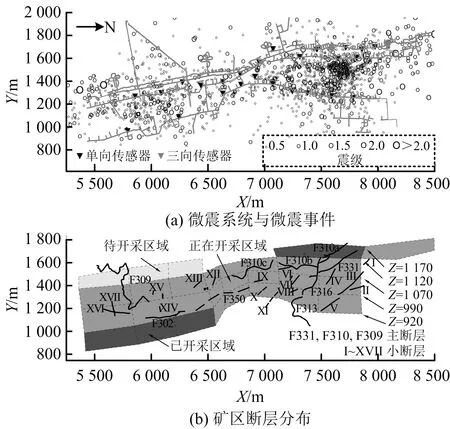
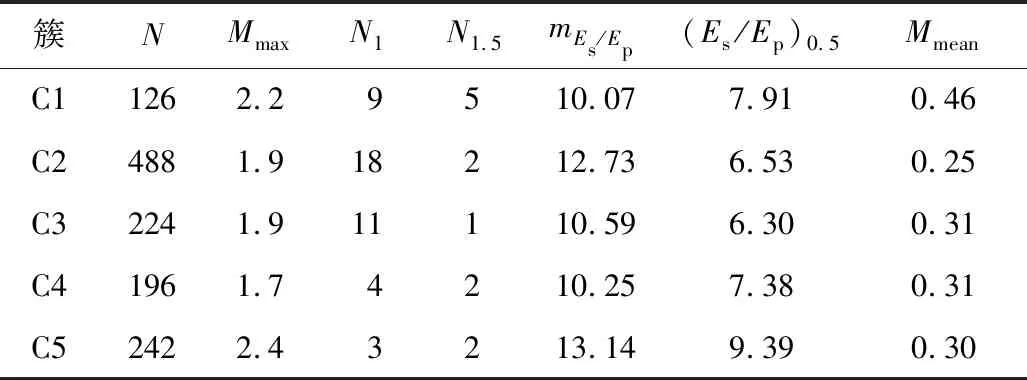
1)存在至多k-1 個對象xi′∈X(xi′≠xi)且dist(xi′,p) 2)存在至少k個對象xi′∈X(xi′≠xi)且dist(xi′,p)≤dist(xi,p),則對象p的第k距離記為k-dist(p)=dist(xi,p)。圖1說明了k=6時,對象p1的第k距離k-dist(p1)。 圖1 k=6時的第k距離領域與可達距離Fig.1 k-distance neighbourhood and reachability distance, when k=6 定義2:對象p的第k距離領域Nk(p) Nk(p)指對象p的第k距離內所有對象組成的集合(包括第k距離)。|Nk(p)|是指對象p的第k距離領域內所有對象的個數,且|Nk(p)|≥k。圖1對象p1的|Nk(p1)|為7,對象p2的|Nk(p2)|為6。 定義3:對象xi相對于對象p的可達距離 令k為正整數,對象xi相對于對象p的可達距離計算如下: reach-distk(xi,p)=max(k-dist(p),dist(xi,p)) (1) 圖1中,對象xi相對于對象p1的可達距離為reach-distk(xi,p1)=k-dist(p1),對象xi相對于p2的可達距離為reach-distk(xi,p2)=dist(xi,p2)。 定義4:對象xi的局部離群因子 對象xi的局部離群因子LOFk(xi)的定義如下: (2) 式中:lrdk(xi)是指對象xi的局部可達密度(Local Reachability Density),定義如下: (3) 由公式(2)~(3)可知,對象xi的LOF值越小,說明其局部可達密度越大,越接近局部中心;對象xi的LOF值越大,說明其局部可達密度越小,越接近局部邊緣,為異常事件的可能性越大。 數據集中的異常事件容易影響K-means聚類結果,因此聚類前需檢測和剔除異常事件。首先,利用公式(2)計算數據集X中每個對象xi的LOF值,再將所有對象xi的LOF值按升序排列,并進行歸一化處理;然后,將所有對象xi的歸一化值進行升序排序,并計算出其拐點值,將此值作為異常事件和正常事件的臨界值[16]。如果對象xi的歸一化值大于拐點值,則剔除對象xi;反之,則留下對象xi。高斯分布的歸一化公式如下[17]: (4) 本文選取初始聚類中心的思路為:選擇去除異常事件數據集中,LOF值最小的對象xi作為聚類算法的第1個初始聚類中心;然后,將與第1個初始聚類中心距離較遠且全局密度較大的對象作為第2個初始聚類中心;接著,將與前2個初始聚類中心的均值相距較遠且全局密度較大的對象作為下1個初始聚類中心,直到計算得到與聚類分組數相同的聚類中心數為止。具體如下: 2)計算第2個初始聚類中心,直到第K個初始聚類中心。 (5) LOF-K-means聚類算法實現過程如下: Input:數據集X={x1,x2,…,xn},聚類分組數K,第k領域值k。 Step2:用2.1.2節的方法選取初始聚類中心。 LOF-K-means聚類算法采用拐點值判別異常事件,較人為判別更加客觀。同時,用LOF值最小的對象,即所在區域密度最大的對象作為第1個聚類中心,可以適應更廣泛類型的數據集,避免出現數據集類型或者大小的改變對聚類算法產生的影響。 1)聚類效果評價 采用函數簇內誤差平方和(within-cluster Sum of Squared Errors, SSE)評價聚類效果,SSE值越小說明各類間分隔越明顯,聚類結果越好。 (6) 2)聚類數選取指標 采用KL指標確定聚類數,Krzanowski和Lai[18]通過計算2個連續不同分組數的聚類結果的簇內協方差矩陣的跡來確定最佳聚類分組數。KL指數值越高,其對應分組數的聚類結果越好。對于聚類分組數K≥2的數據集X={x1,x2,…,xn},xi∈Rd,KL指標的定義如下: (7) 為測試本文方法的優越性,選取傳統K-means聚類和文獻[14] K-means聚類算法作為對比。不同聚類方法的聚類效果可能受數據集的大小影響,本文選取數據集包含100,250,500,750和1 000個對象進行討論。同一數據集分別運用上述3種聚類算法進行聚類計算,使用的聚類參數為x, y軸坐標,第k領域設為20。首先計算上述3種聚類方法在同一數據集、同一個分組數下的SSE值,SSE值由小至大分別記為①,②和③,根據表1進行比較得到評分,見表1。例如:LOF-K-means聚類、傳統K-means聚類和文獻[14] K-means聚類算法的SSE值分別為100,200和150時,那么該SSE值由小至大排列后,對應表1中的評價工況4,且LOF-K-means聚類、傳統K-means聚類和文獻[14] K-means聚類算法評分分別為2,0和1。再將每1種聚類算法在2~10個聚類分組下得到的評分相加,得到總評分作為該聚類算法的綜合SSE評價指標,其值越大則說明該聚類算法越好。為減少個別聚類結果對不同聚類方法的影響,將每種數量規模的數據集分別隨機生成100次進行聚類計算,得到這3種聚類方法的綜合SSE評分。圖2為數據的聚類過程。可知初始聚類中心的選取與數據集的分布有關,且與數據集的局部密度緊密聯系。 表1 不同SSE工況下評分Table 1 Scoring for different SSE conditions 注:①~③分別對應SSE值從小到大排列的3種聚類方法。 圖2 數據集的聚類過程Fig.2 Clustering process of dataset 模擬測試的結果如圖3所示,當數據集事件數為100,250和1 000時,LOF-K-means聚類綜合SSE評分的中位數最大;當事件數為500和750時,其中位數與文獻[14] K-means聚類的相同,上四位數與文獻[14] K-means聚類的相同或較大,兩者均比傳統K-means聚類的評分大。 圖3 不同數據集大小的聚類結果Fig.3 Clustering results for different sizes of dataset 總的來說,對于不同事件數大小的數據集,LOF-K-means聚類算法的聚類效果最好,文獻[14] 的聚類方法次之,傳統K-means聚類方法效果最差。 本文實例所用的數據來源于用沙壩礦微震監測系統,其位于貴州省中部,東經106.81°,北緯27.08°。礦體呈穩定的層狀,礦體厚度穩定,沿走向和傾向連續性較好,傾角為10°~55°,磷礦的年產量超過200萬t且已探明的礦石儲量為4 000多萬t。2013年開始,在用沙壩礦區建立了礦山IMS微震監測系統,主要用來監測礦區內的微震活動。IMS微震監測系統由28個傳感器組成 ,如圖4(a)中三角形區域,其中單向傳感器有26個,三向傳感器有2個;主要分布在920中段,1080中段和1120中段。圖4(a)說明礦山微震事件主要分布在巷道區域,圖4(b)為礦山生產活動區域和斷層分布,可知微震事件分布與生產活動區域和斷層分布具有較好的吻合性。一般認為較大震級微震主要受斷層影響,本文選取了較大震級的事件(M≥0)展開分析[11],嘗試將微震事件與斷層活動聯系起來。 圖4 用沙壩礦區的微震系統與斷層分布Fig.4 Microseismic system and fault distribution in Yongshaba mine 本文使用的數據集為2014年1-6月測得的1 649個矩震級大于等于0級的微震事件,如圖4(a)中圓形所示。采用LOF-K-means聚類算法,使用的聚類參數為微震事件的x,y,z軸坐標,所取的第k領域為k=90。聚類后的KL指數如圖5所示,可知較好的聚類分組數為2,5和7。 圖5 LOF-K-means聚類的微震事件KL指數Fig.5 KL index of microseismic events by LOF-K-means clustering 圖6給出了聚類分組數K為2,5和7的微震事件聚類結果,參照文獻[11],選取的一些重要聚類參數值見表2~4。從圖6(a)可知,K=2時,礦區的微震事件由斷層F310c和斷層F350劃分為左右兩簇。分析可知,C1簇主要受主斷層F310,F313和斷層F316,F331的影響;C2簇主要受主斷層F309,F350和F302的影響。結合表2,可以解釋這2個聚類簇主要依據區域斷層結構間的作用,而引起微震事件的影響程度進行劃分。C1簇和C2簇的mEs /Ep值大于10,且C2簇的(Es/Ep)0.5為8.07比C1簇的大,說明C2簇受斷層的影響更大。 表2 K=2時,不同聚類簇的微震參數Table 2 Microseismic parameter of different clusters,when K=2 表3 K=5時,不同聚類簇的微震參數Table 3 Microseismic parameter of different clusters,when K=5 表4 K=7時,不同聚類簇的微震參數Table 4 Microseismic parameter of different clusters,when K=7 注:N指簇內微震事件數;Mmax指簇內最大的震級;N1指簇內震級≥1.0的微震事件數;N1.5指簇內震級≥1.5的微震事件數;mEs/Ep為簇內S波與P波能量比的均值;(Es/Ep)0.5為簇內S波與P波能量比的中位數;Mmean為簇內平均震級。 圖6 用沙壩礦微震事件LOF-K-means的聚類結果Fig.6 LOF-K-means clustering results of microseismic events in Yongshaba mine 從圖6(b)可知,K=5時,C1簇受斷層I的影響,C2簇和C3簇沿著主斷層F310a,F316和F313劃分;C4簇受主斷層F350和F302影響;C5簇受主斷層F309和斷層XVII,XVI的影響。結合表3,C1簇的事件數最少,但N1.5有5個;mEs/Ep大于10,(Es/Ep)0.5與其他簇相比處于較大值且Mmean最大,說明C1簇主要受斷層滑移的剪切作用影響,推測主斷層F310或F331可能延伸到C1簇區域。C2簇的事件數最多,mEs/Ep大于10,N1有18個,N1.5有2個,說明其受到斷層滑移的影響;但Mmean最小且(Es/Ep)0.5較小,說明其也受到礦山生產活動的影響,且影響作用比斷層滑移的大。C3簇與C2簇類似,受到礦山生產活動和斷層滑移共同影響。C4簇與C5簇所在區域較難描述,但C5簇mEs/Ep大于10且(Es/Ep)0.5接近10,說明其基本受斷層滑移的剪切作用影響。 從圖6(c)可知,K=7時,C1簇與K=5時的C1簇基本相同,C2簇主要受主斷層F310a和F331的影響,C3簇與C4簇沿著主斷層F313和F316劃分;C5簇受主斷層F350的影響;C6簇受主斷層F302的影響且沿著F309與C7簇劃分。C2 簇與C3簇的各項微震參數基本相同,且與K=5時的C2簇相似,說明主要受到各斷層滑移和礦山生產活動共同影響。C4簇與C3簇類似,但Mmax和Mmean較大,說明其受到各斷層滑移和礦山生產活動共同影響,相對受斷層滑移的影響程度較大。C5簇的事件數較少但N1.5有2個,且mEs/Ep和(Es/Ep)0.5都大于3不到10,說明該區域由斷層滑移和礦山生產活動共同作用;且從微震事件數量上看,礦山生產的影響較小,斷層滑移的影響較大。C6簇可作為由礦山生產造成微震事件典型的集群,事件數較多且Mmean和Mmax最小,說明其由礦山生產活動影響,雖然其mEs/Ep和(Es/Ep)0.5均大于3,但綜合分析仍可認為C6簇主要處于礦山生產活躍區域。C7簇mEs/Ep和(Es/Ep)0.5均大于10,N1.5有2個,Mmean為0.31,說明主要受斷層滑移剪切作用的影響。總的來說,K=7時各簇微震事件的分布效果較好,可以更好的解釋微震活動性特征。 K=7時聚類簇事件的時鐘矢量圖如圖7所示。由圖7可知,C1,C5和C6簇微震事件初期發生時間集中在12∶00方向,后逐漸轉向13∶00~14∶00;C2,C3,C4和C7簇微震事件發生時間主要在13∶00~14∶00。7個聚類簇微震事件的軌跡曲線都超出圓,說明礦區微震事件受生產活動影響。用沙壩礦區的生產爆破時間集中在11∶00~13∶00,則爆破期間和爆破后的1~3 h內是微震事件頻發期。 圖7 K=7時聚類簇事件的時鐘矢量Fig.7 Clock vectors of clustering events ,when K=7 1)針對K-means聚類易受異常事件和初始聚類中心影響的問題,引入了LOF算法進行異常事件的檢驗和初始聚類中心的選擇,提高了聚類結果的有效性。 2)建立了聚類算法的綜合SSE評價指標,通過計算模擬比較了在不同數據集大小下,LOF-K-means聚類算法、文獻[14] K-means聚類算法和傳統K-means聚類算法的綜合SSE評價指標,得到LOF-K-means聚類算法最優。 3)將LOF-K-means聚類算法用于分析用沙壩礦微震事件分布特征,得出最佳分組數為7。其中C1,C7簇主要受斷層滑移的影響;C6簇主要受礦山生產活動的影響,為礦山微震活動性分析提供了一種有效的方法。
2 聚類算法的優化
2.1.1 異常事件檢測
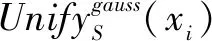
2.1.2 初始聚類中心的選擇
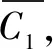

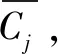
2.1.3 LOF-K-means聚類算法
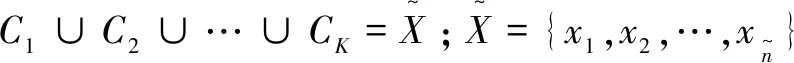



2.1.4 評價指標


3 模擬測試

4 礦山微震監測應用
4.1 用沙壩礦微震系統
4.2 礦山微震事件的聚類分析





5 結論

