梯度域和深度學習的圖像運動模糊盲去除算法

郭業才, 鄭慧穎， 葉 飛

(南京信息工程大學 a.江蘇省大氣環境與裝備設計協同創新中心, b.電子與信息工程學院， 南京 210044)

0 引 言

在獲取圖像時，可能由于外界環境或成像設備等原因，使得圖像存在不同程度的退化降質，如模糊、噪聲等，這些退化降質的數字圖像對人們的生產生活有著極大的影響。因此，去除模糊，得到清晰圖像非常重要。現有的圖像去模糊算法主要有:①利用自然圖像的邊緣先驗信息恢復清晰邊緣[1-7]。這些先驗信息對圖像去模糊是有效的，但需要解決非凸性問題。此外，優化方法和模糊核估計過程均很復雜，會導致計算成本較高。②運用深度學習網絡實現圖像去模糊[8-15]。目前，利用深度學習的方法實現圖像去模糊，在去卷積的過程中會使圖像過于平滑，導致圖像的高頻信息和圖像紋理細節丟失，這樣不僅花費時間較長，而且會導致圖像的振鈴效應更加明顯。

本文針對現有圖像去模糊方法的不足，提出一種基于梯度域和深度學習的圖像運動模糊盲去除算法。該算法利用圖像梯度域減少無關細節的影響，提高模糊核估計的魯棒性。結果表明，該算法在有效保持邊緣信息、顯著減少振鈴效應的同時，去模糊效果較好。

1 圖像去模糊原理及方法

圖像降質退化過程如圖1所示。輸入圖像x，在模糊核k和噪聲n影響下，得到模糊圖像為

y=k[x]+n

(1)

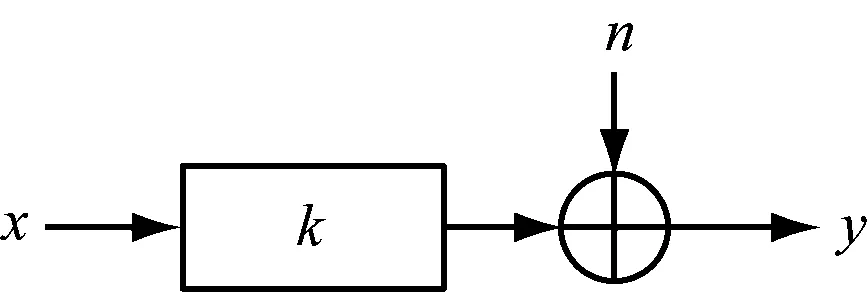
圖1 一般圖像退化模型

圖像盲去模糊即模糊核未知，需要從模糊圖像y中獲取清晰圖像x和模糊核k。盲去模糊問題可以將求解出的模糊核轉變為非盲去模糊問題，即

(2)

式中：?表示卷積操作；式中第1部分是數據保真項，利用L2范數進行約束；第2部分是先驗正則約束項，它與原始清晰自然圖像有關，λ是使約束項和數據保真項之間比例平衡的參數，正則項的選擇與選取的圖像先驗有關。

圖像盲反卷積問題的不適定性可以通過正則化方法解決，本文通過CNN的容錯能力、并行處理能力和自學習能力，將CNN可以學習圖像自身特征的性能用于去模糊的問題中，設計了一個有效的CNN網絡結構。

2 圖像運動模糊盲去除算法

2.1 圖像預處理

首先，將引導濾波[16]后的圖像作為基礎圖像，以減少噪聲和多余細節的影響。然后，將L0濾波[5]后梯度域圖像以及對應的清晰圖像作為樣本，對設計的CNN進行訓練。本文中，引導濾波和L0濾波都是作用在清晰圖像上的，可以抑制無關細節，增強圖像的清晰邊緣，提高了模糊核估計的魯棒性。圖2為圖像預處理部分的結構流程圖。

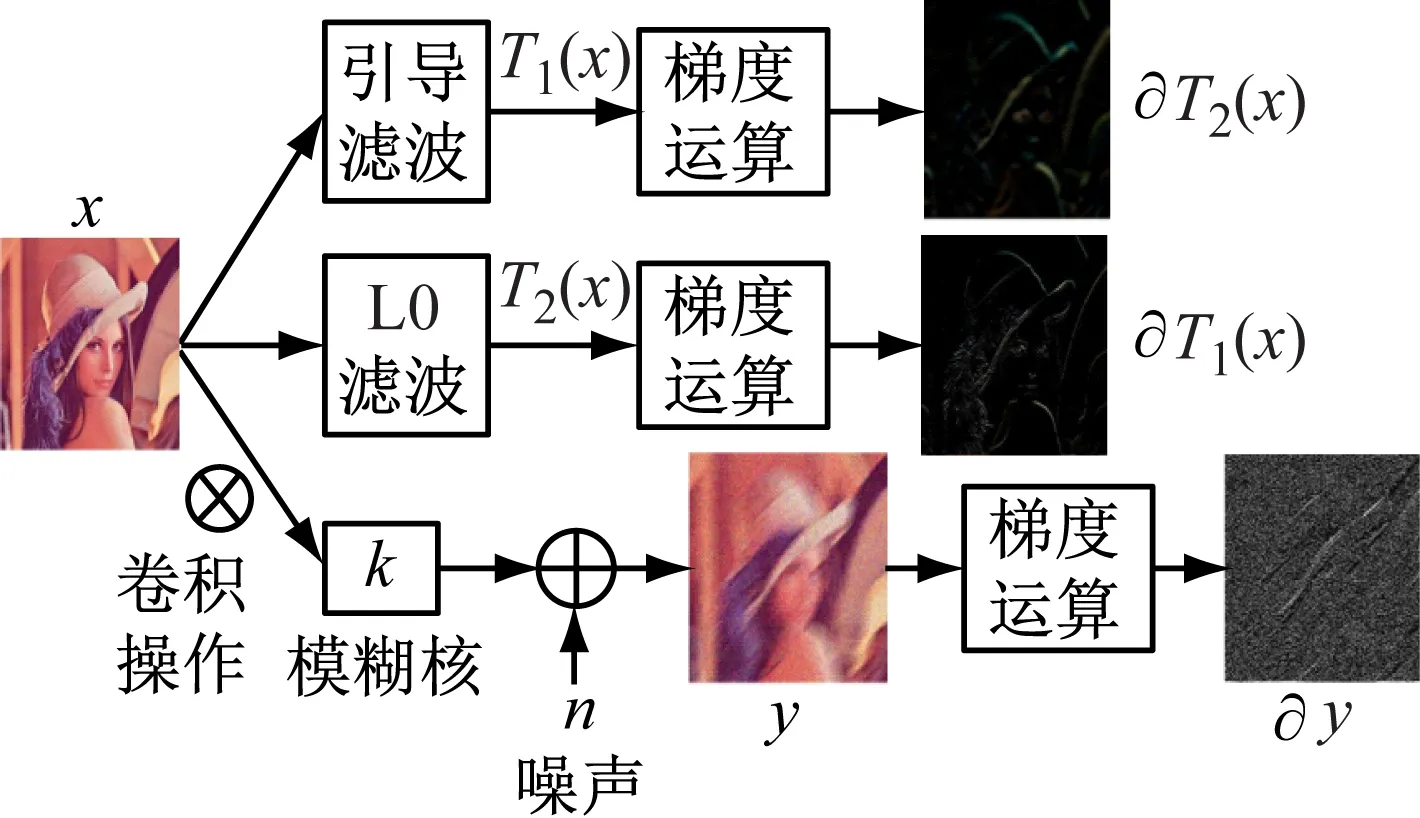
圖2 圖像預處理部分的結構流程

在利用濾波實現圖像去模糊的基礎上，提出利用引導濾波對圖像進行預處理，因為通過引導濾波可抑制圖像中的無關細節，并且保留圖像的主要結構，如圖3所示。其中，圖3(a)是清晰圖像；圖3(b)是運動模糊噪聲圖像；圖3(c)是清晰圖像經過引導濾波后的圖像；圖3(d)是與清晰圖像像對應的梯度域圖像；圖3(e)是模糊圖梯度域圖像；圖3(f)是清晰圖像經過引導濾波后的梯度域圖像。

(a)(b)(c)(d)(e)(f)

圖3 引導濾波處理結果圖

2.2 卷積神經網絡結構設計

文獻[17]中提出利用梯度域圖像訓練CNN結構，而本文對文獻[17]中的網絡結構進行改進，提出利用較大卷積核提取圖像的細節信息；加深網絡層數使網絡訓練得到的權重數據更加準確。

現利用梯度域對網絡進行訓練。網絡的輸入分別經過引導濾波和L0濾波后的梯度域圖像與其對應的模糊圖像，輸出為圖像的邊緣信息。把輸入圖片旋轉90°后提取其邊緣信息，與不旋轉時提取邊緣信息得到的效果相同，因此本方法僅利用垂直方向的梯度對網絡進行訓練，并在水平和垂直方向上共享權重，如圖4所示。

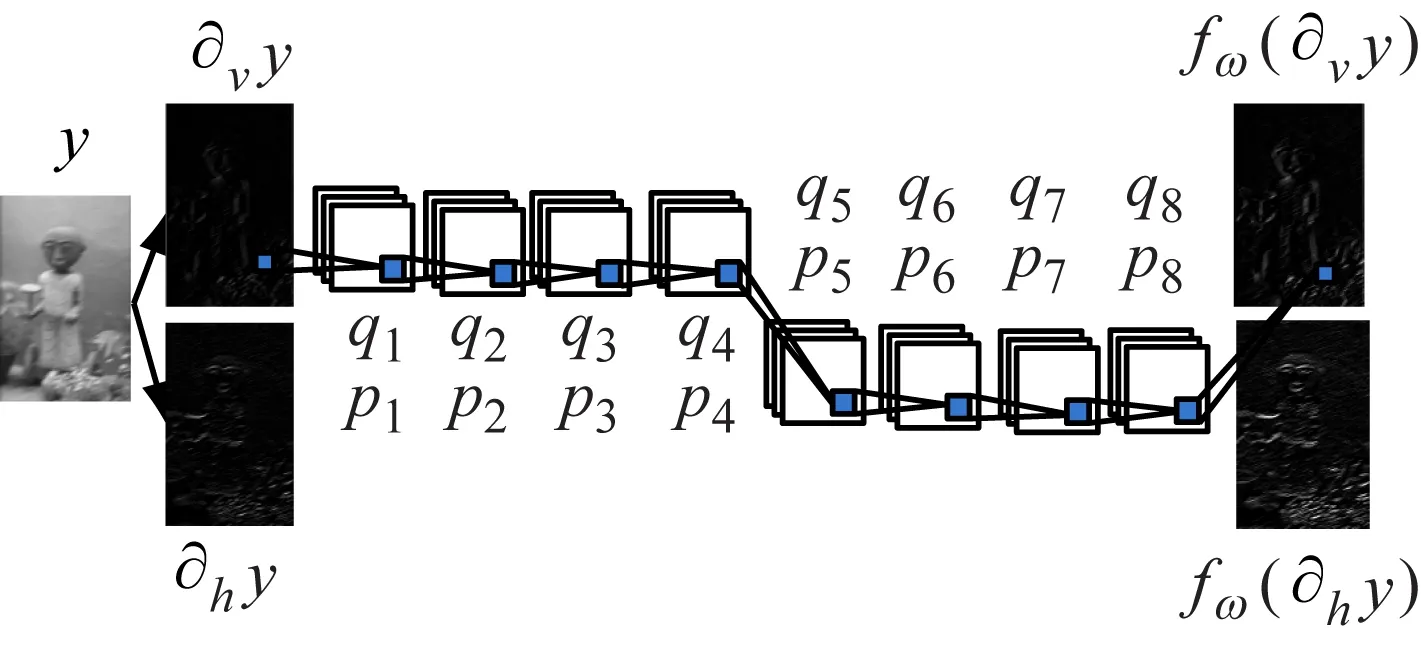
圖4 網絡結構

由圖4可得：

f0(?y)=?y

(2)

(3)

l=1,2,…,7

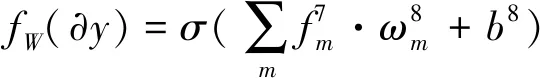
(4)

(5)

式中，{αm}是可學習的系數。

通過一組圖像對D{?yi,?T1(xi)}，網絡的第1階段可以描述為問題：

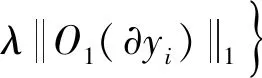
(6)

式中：D表示真實圖像和模糊圖像的訓練對；采用基于L1損失的TV正則化方法對圖像梯度進行稀疏化處理；λ是正則化的權重。由于L1范數在0處不可微，因此利用Charbonnier函數，即ρ(z)=(z2+ε2)1/2來估計它。目標函數可寫為

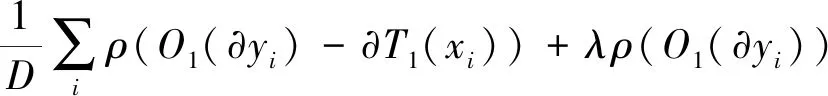
(7)

為了訓練第2階段的網絡，最后3層的輸出為:

(8)

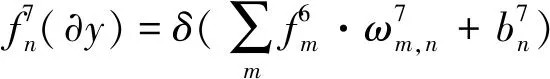
(9)

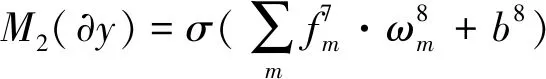
(10)

式中，gn是尺寸為q6×q6可學習的卷積核。

通過一組圖像對D{?yi,?T2(xi)}，網絡的第2階段可以描述為問題：

(11)

兩個子網絡訓練完后，將這兩個子網絡結合為

(12)

式中，m=1,2,…,p5；n=1,2,…,p6。

整個網絡訓練過程loss值為

(13)

式中：ρ(z)=(z2+ε2)1/2，ε取10-6；λ為正則項的權重；fω(?yi)是網絡訓練得到的邊緣信息。

2.3 圖像去模糊

2.3.1 模糊核的估計

(14)

式中：參數η控制k的平滑度。第1項提供可靠邊緣信息，第2項約束模糊核稀疏性，第3項

C(k)={(x,y)||?xk(x,y)|+|?yk(x,y)|≠0}

它的作用是使模糊核稀疏，也阻止出現不連續點，從而提高模糊核的連續性。

由于式(14)涉及到離散數值計算，因此很難直接對它求解最小值，本文將式(14)描述為：

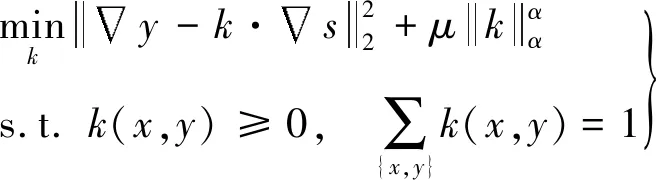
(15)

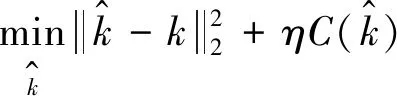
(16)

式(15)可以利用IRLS方法[19]求得，實驗中，一共進行了3次迭代；式(16)可以通過交替優化[20]的方法求得解，一共進行了3次迭代。通過對上面兩個子式的求解，最終可以得到模糊核k。

2.3.2 最終的潛像估計

得到模糊核后，最終潛像可通過非盲解卷積的方法獲得。本文主要恢復運動模糊圖像的邊緣，采用TV正則化進行最終潛像的恢復，即

(17)

3 實驗結果及分析

3.1 運動模糊圖像生成

采用的圖像數據庫是BSDS500中的自然圖像，為了獲得模糊圖像yi，對每一張清晰圖像xi進行模糊處理。假設運動模糊是全局線性模糊，模糊核k=(l,o)受到長度和角度的影響。選取運動模糊的長度l從1～25，以2為間隔，角度o從0°～150°，以30°為間隔。由于當模糊核長度l=1時，不管運動方向是什么，所有的運動向量都對應著相同的模糊核，因此生成73個不同的模糊核。將這73個不同的模糊核與BSDS500中的500張自然圖像xi進行隨機卷積，再加上1%的高斯白噪聲，就可以產生運動模糊圖像。將產生的運動模糊圖像裁剪成大小為45×45的模糊圖像塊，獲得最終所需的模糊圖像yi。本文通過給定模糊的圖像yi，根據提出的方法首先計算垂直和水平方向的圖像梯度，以梯度域圖像作為卷積神經網絡的輸入。

3.2 網絡結構

為了找到對圖4所示結構作貢獻的參數，進行了兩組實驗。兩組實驗中，CNN層數相同，每層濾波器數量不同，濾波器的大小不同。通過比較兩組實驗使用同一數據集在訓練期間的loss值，來分析不同參數對實驗結果的影響，如圖5和圖6所示。

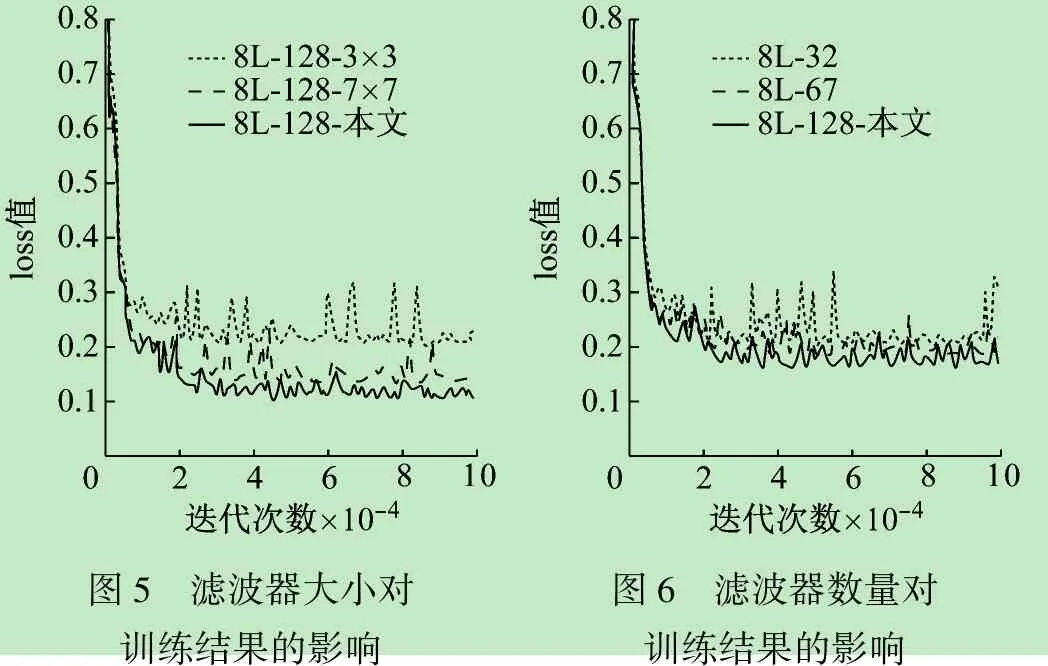
圖5 濾波器大小對訓練結果的影響圖6 濾波器數量對訓練結果的影響

訓練整個模型一共進行10萬次迭代，圖5表示濾波器大小對訓練結果的影響。整個網絡一共8層，每層濾波器的個數均為128個。圖中：紫色曲線是在大小不同的濾波器下獲得的；藍色曲線是在整個網絡均使用5×5的濾波器下獲得的；紅色曲線是在整個網絡均使用7×7的濾波器理獲得的。圖6表明，3種loss曲線約在85 000次時開始收斂，但本文方法采用不同大小濾波器時的loss值皆都低于其他兩種情況。這表明，本文所選擇的濾波器大小是合理的。

圖6表示濾波器的數量對訓練結果的影響。本實驗的網絡一共有8層，每層濾波器的大小均如圖4所示，分別選取每層濾波器數量為64個和32個，與本文每層濾波器數量為128個進行對比。圖中：紫色曲線是本文采用每層128個濾波器時獲得的;藍色曲線為網絡每層使用64個濾波器時獲得的，紅色曲線為網絡每層使用32個濾波器時獲得的。圖5表明，3種loss曲線大約在60 000次時開始收斂，但本文采用每層濾波器數量為128時的loss值均低于其他濾波器數量所對應的值。這表明，本文所選擇的濾波器的數量是合理的。

3.3 去模糊效果

采用峰值信噪比(Peak Signal to Noise Ratio，PSNR)對去模糊的效果進行分析：

(18)

式中，T指圖像像素強度的最大值。

去模糊效果分別與多層神經網絡(Multi-layer Perceptron，MLP)方法[10]和邊緣檢測方法[21]進行對比。MLP方法利用多層感知器實現圖像去模糊；邊緣檢測方法將圖像結構與優化算法相結合應用于圖像去模糊，如圖7所示。

圖7 去運動模糊效果

圖7選取4張圖像在不同模糊程度下，分別運用MLP方法、邊緣檢測方法及本文方法對圖像進行去運動模糊。其中：圖7(a)為原始清晰圖像；圖7(b)為模糊噪聲圖像；圖7(c)為使用MLP方法去除運動模糊后的結果圖，圖7(d)為使用邊緣檢測方法去除運動模糊后的結果圖，圖7(e)為使用本文提出的算法去除運動模糊后的結果圖。PSNR值如表1所示。由表1知，MLP方法與邊緣檢測方法去除運動模糊的PSNR值相差不大，但是MLP方法會放大噪聲，邊緣檢測方法可能會給圖像帶來振鈴效應。而本文方法的PSNR值在對比實驗中值均明顯高于其他兩種方法，而且放大噪聲與振鈴效應均不明顯，去運動模糊效果明顯優于其他兩種方法，這就表明本文算法能夠有效地移除圖像運動模糊。

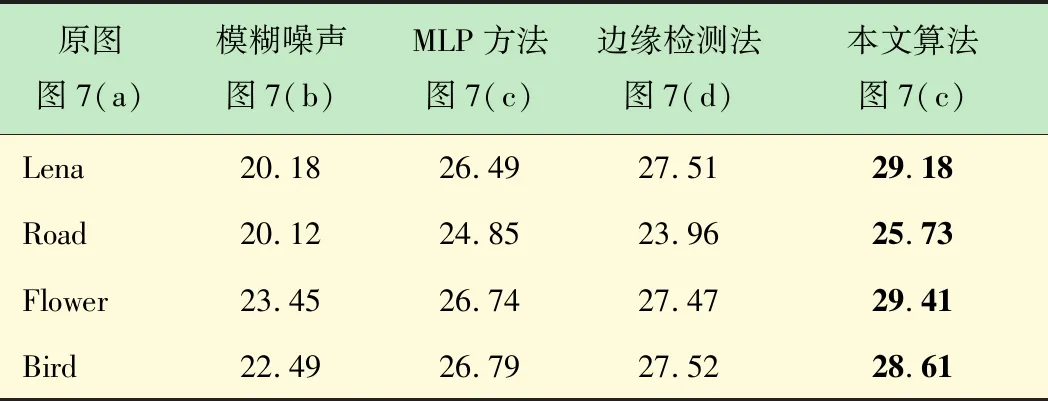
表1 不同方法的PSNR值 dB

4 結 語

本文提出一種基于梯度域和深度學習的圖像運動模糊盲去除算法，將CNN可以學習圖像自身特征的性能用于去模糊的問題中，設計了一個有效的CNN結構;將圖像梯度域預處理與CNN網絡相結合的方法，避免直接用CNN網絡而忽略圖像先驗信息的缺點。實驗表明，本文方法不僅能有效去除圖像運動模糊，同時很好地保留了圖像細節，放大噪聲不明顯，較好地抑制了振鈴效應的產生。