基于投影尋蹤聚類方法的邊坡穩定性分析

李佳偉，李 婷，顧中明，張 琪

(1.四川蜀禹水利水電工程設計有限公司，四川 成都 610072；2.南京水利科學研究院，江蘇 南京 210024；3.云南水利水電建設工程技術開發有限公司，云南 昆明 650021；4.樂安縣煙草專賣局，江西 撫州 344300)

邊坡穩定性分析評價一直以來都是土木工程中的重要課題和難點[1-2]。邊坡穩定性受多重因素的影響[3]，安全系數法是衡量邊坡穩定的常規方法，但同一安全系數往往具有不同的安全性。常用的邊坡穩定評價方法有灰色聚類、熵值法確定權重、模糊評價等基于均值和權重的評價方法[4-5]。這些方法，一方面，對于非線性、高維的邊坡穩定影響因素分析存在很多不確定性[6]；另一方面，沒有理論依據的權重賦值，導致結果受人為干擾因素過大。因此，這些方法存在一定的局限性或適用范圍。投影尋蹤是一種將高維數據投影到低維空間上，尋找能夠反映原高維數據的結構特征的投影，從而分析高維數據規律的方法。司俊燕等[2]使用粒子群優化算法結合投影尋蹤聚類方法對錦屏一級水電站邊坡穩定進行了分析，將邊坡穩定性能分為五個等級；汪明武等人[5]利用加速遺傳算法結合投影尋蹤聚類方法對12個典型崩滑體邊坡進行了分析；金永強等人[7]，使用和聲搜索和投影尋蹤聚類方法，分析12個邊坡案例。綜上，投影尋蹤聚類結合人工智能算法，在的邊坡穩定性分析中得到了充分的運用。

本文以馮夏庭[8]書中記載的典型的82個圓弧破壞型邊坡工程實例數據為驅動，建立投影尋蹤聚類模型，采用遺傳算法實現對樣本的自動聚類尋蹤和投影方向擬合，并對其適用性進行分析。

1 投影尋蹤聚類模型建立

1.1 原理方法

在邊坡穩定分析中，假設對邊坡穩定主要影響因素有m個，共收集到n個邊坡實例，即將n個實例組成樣本集xij(i=1,2,…,n；j=1,2, …,m)，其中xij為第i個案例的第j個指標值。綜合成投影方向a={a(1),a(2), …,a(n)}上的投影序列值{z(i)|i=1,2,…,n}，通過構造投影指標Q(a)實現各案例的邊坡穩定性進行聚類，并用遺傳算法進行優化求解，以Q(a)最大化時的a*值，來確定投影值Z(a)并評價邊坡的安全性能大小。

步驟 1：邊坡影響因素歸一化處理

對于越大越優的指標：

(1)

對于越小越優的指標：

(2)

步驟2：構造投影函數

(3)

a=(a(1),a(2), …,a(m))為m維數據{x(i,j)|j=1～m}的投影方向，{z(i)|i=1～n}為投影值，依據投影值進行分類。

步驟3：構造投影指標函數

構造投影指標函數，投影指標函數的優劣，以投影值z(i)局部之間凝聚效果和投影局部與局部之間的分散效果為判斷指標。最優的投影值z(i)分布特征應達到局部盡可能聚集，局部與局部間盡可能分散。其數學實現途徑如下：

2.4.2 不同性別的醫務人員院感知識認知正確率比較分析 不同性別醫務人員的問卷總體認知正確率差異并無統計學意義（P＞0.05），進一步對問卷的7個方面逐一比較后發現，醫院污物處理認知正確率男性醫務人員高于女性醫務人員，差異有統計學意義（P＜0.05）。在其余6個方面男女認知正確率差異無統計學意義（P＞0.05）。

Q(a)=SzDz

(4)

其中，Q(a)為投影指標函數，Sz為投影值z(i)的標準差:

(5)

Dz為投影值z(i)的局部密度：

(6)

其中，Ez為投影均值；R為投影局部密度的半徑，R的值不宜過大，過大會導致局部投影分區不明顯，也不宜過小，過小會導致投影聚類效果下降。rij=|z(i)-z(j)|，表示不同樣本間的投影差值；u(R-rij)為單位階躍函數，當R-rij≥0時u值為1，當R-rij<0時u值為0。

步驟4：優化投影指標函數——基于遺傳算法確定最佳投影方向

投影指標函數Q(a)的取值僅受投影方向a的影響，將最佳投影方向定義為多影響因素下的最大可能暴露邊坡安全性特征的投影方向。通過求解投影指標函數最大化問題來估計最佳投影方向[8]，即：

maxQ(a)=SzDz

s.t.a(j)?[0,1]

以{a(j)|j=1～m}—j個樣本指標為變量的復雜非線性優化問題。

在確定目標函數和約束條件的情況下，采用基于全局優化的遺傳算法來求解最優投影方向[9-10]。確定最優投影方向a*。

步驟5：投影值綜合聚類分析

將a*代入公式(3)，進行聚類計算，得到最優投影值z*(i)：

各投影值z*(i)間相隔越接近，表示樣本之間更易于越傾向為同一類。按z*(i)值從大到小排序，據此可把各指標的樣本集進行分類[1]。

1.2 邊坡穩定投影尋蹤聚類分析實現過程

采用matlab實現上述計算步驟。82個典型圓弧破壞數據中，包含了邊坡穩定影響因素、安全系數值和邊坡穩定狀態。影響邊坡穩定的主要有6個參數[8]：巖石容重γ、巖石粘聚力C、內摩擦系數φ、邊坡角φf、邊坡高度H和孔隙壓力比γu。將這6個參數作為輸入參數，參數分為越大越優的指標和越小越優的指標。為避免因參數間數量級不同造成誤差，同時保留數據間的聯系，對樣本數據進行歸一化。具體實現過程：

1)依據邊坡穩定特性γ、C、φ三個安全系數越大越易趨于穩定，按公式(1)進行歸一化；φf、H和γu越小越易趨于穩定，按公式(2)進行歸一化。

2)適應度函數。依據投影尋蹤算法，建立待優化的函數即適應度函數Sz，遺傳算法一般默認為求極小值，因此優化的函數的目標函數為-Sz。其中，本文中R取值為0.1Sz。

3)調用matlab里的optimtool優化算法。求解器選擇遺傳算法工具ga-Genentic Algorithm。

4)遺傳算法具體參數。約束邊界條件為6個參數的取值范圍，6個參數的上邊界為均為0，下邊界均為1。其他設置采用，默認設置。

5)當matlab計算停止時，輸出使得-Sz最小的最佳投影方向a*；確定各案例在a*下的投影值Z*。并依據Z*的值進行聚類分析。見流程圖1。

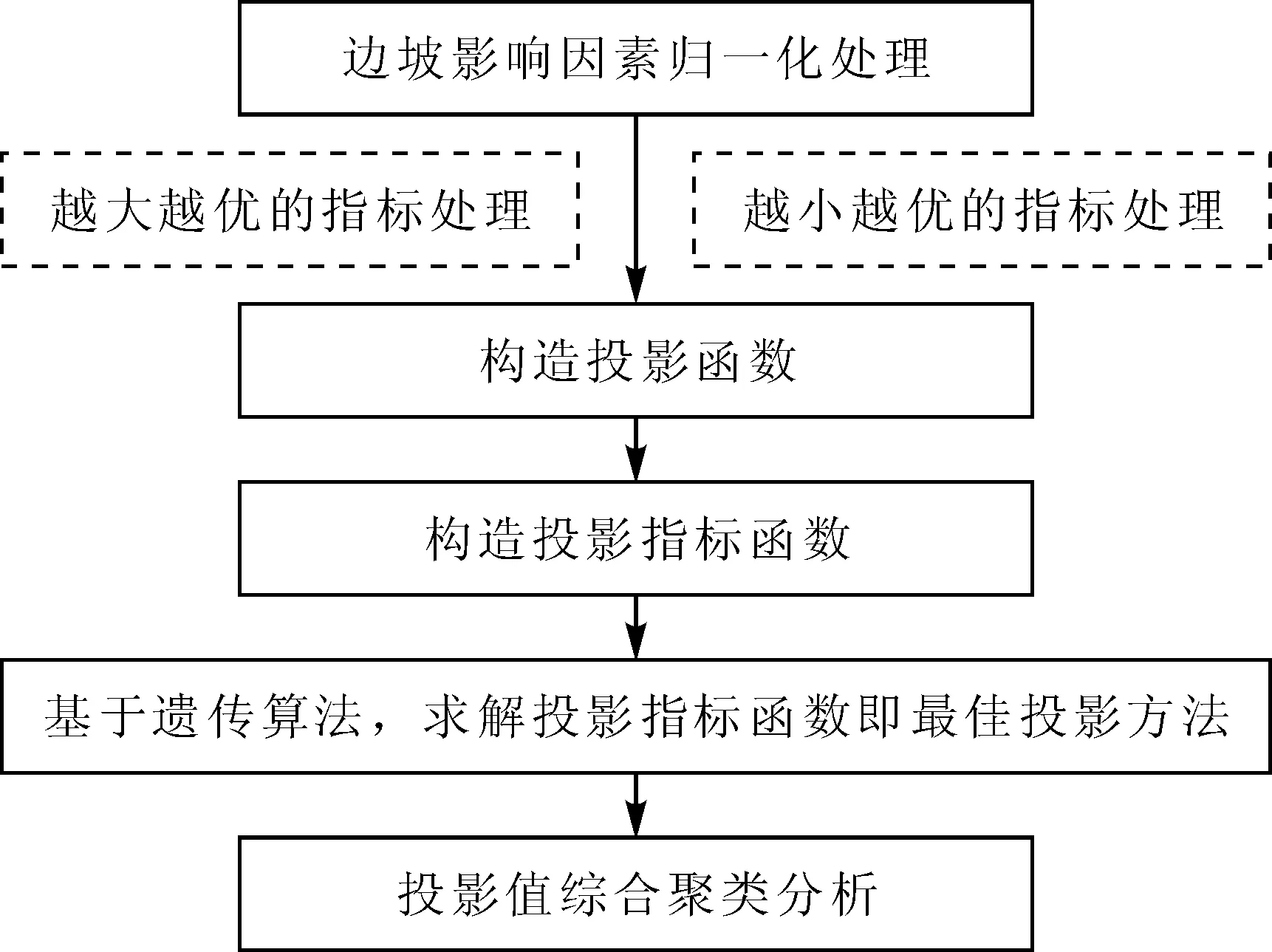
圖1 投影尋蹤聚類流程圖

2 實例分析

2.1 數據及方法

邊坡穩定穩定受多個因素影響[11]，針對不同地質，不同邊坡破壞形式，投影尋蹤聚類法均能進行客觀的聚類分析。本文采用馮夏庭[8]中典型的82個圓弧破壞型邊坡工程實例作為研究對象，并按照書中次序依次編號為1-82，將82個實例按安全系數小于1.2、1.2-1.3、大于1.3分為3組，如圖2。分別進行投尋蹤聚類分析。

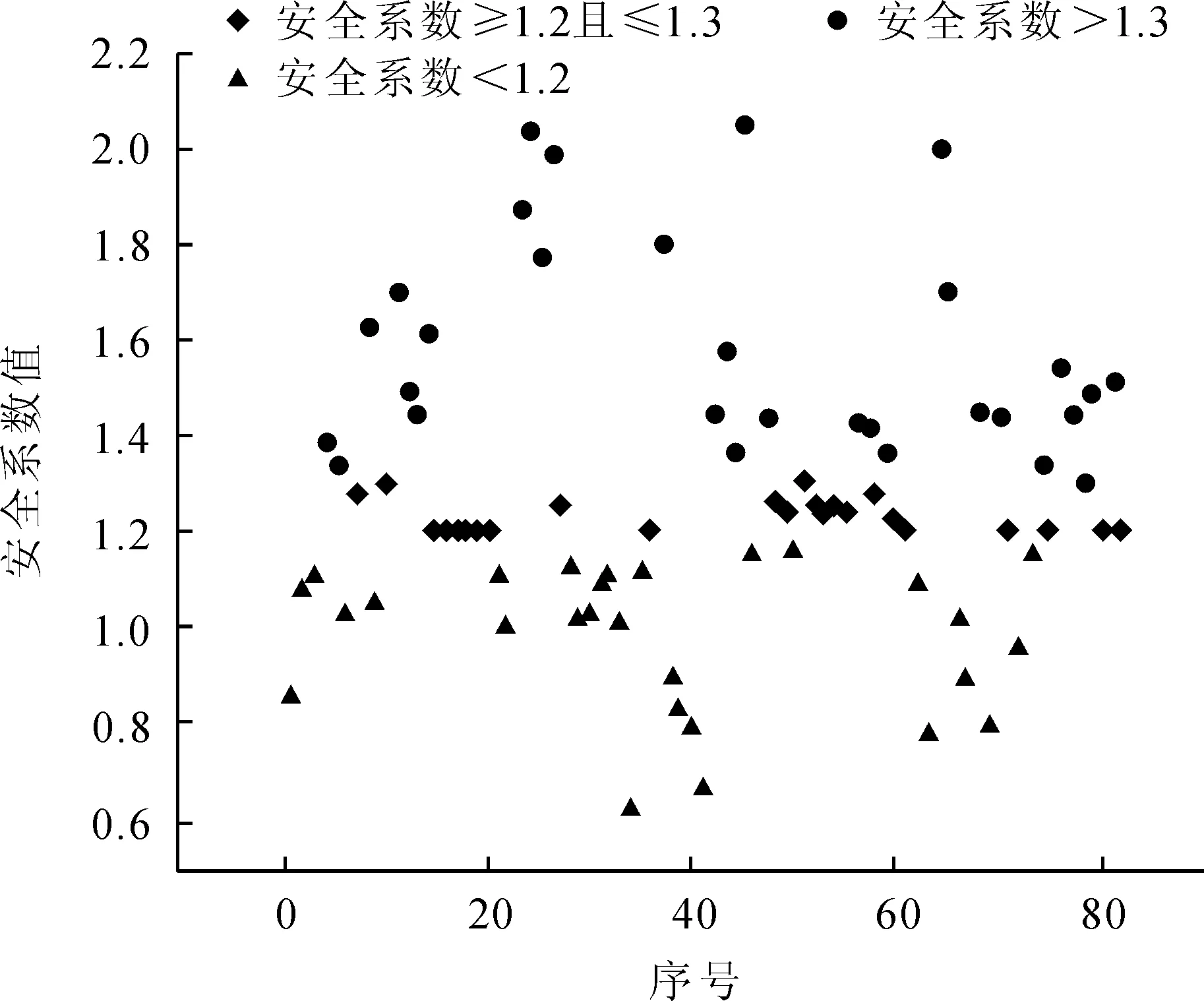
圖2 邊坡工程82個實例安全系數值

2.2 結果分析

投影尋蹤結果，如圖3。不同范圍分布的安全系數案例對應不同的最佳投影方向，其中，投影值越大代表越有利于邊坡穩定。具體分析如下：

1)安全系數小于1.2，樣本量28，按照γ、C、φ、φf、H和γu的順序，確定最佳投影方向a*=[0.966, 0.272, 0.999, 0.063, 0.758,0.686]，投影值見圖(a)，邊坡穩定性貢獻排序為：φ>γ>H>γu>C>φf。

2)安全系數1.2-1.3，樣本量24，最佳投影方向a*=[0.977, 0.820, 0.334, 0.591, 0.196, 0.994]，投影值見圖(b)，邊坡穩定性影響因素排序為：γu>γ>C>φf>φ>H。

3)安全系數大于1.3，樣本量30，最佳投影方向a*=[0.981, 0.335, 0.794, 0.008, 0.013, 0.998]，投影值見圖(c)，邊坡穩定性影響因素排序為：γu>γ>φ>C>H>φf。

聚類分析。按照投影值大小進行聚類結果等級劃分，投影值相近的認為是同一等級即同類。聚類分析的目的是在安全系數確定的情況下，可以再次對各案例進行穩定排序，以便從多角度對邊坡的穩定性進行判斷。顯然，在案例數較多的情況下，對投影值劃分越細，聚類過程中會產生越多的分類。本文以投影值相差0.2-0.4為判斷區間，并盡可能多的包含案例數量。按階梯狀較好的化為同類，當投影值階梯狀案例數小于4個時，歸為同類的投影值相差范圍可適當的放大。通過聚類分析，投影值大小進行聚類結果如圖3所示。圖(a)、(b)、(c)的安全系數變化范圍依次為0.6-1.2、1.2-1.3、1.3-2.1。按聚類效果(a)、(c)可分為四類，其中穩定性由高向低排序依次為四類、三類、二類、一類。其中，(a)和(c)由于安全系數變化范圍較大，樣本間的相似性不足，導致聚類值和安全系數計算結果存在較大的差異，該情況下聚類結果不足以作為判斷安全性能差異的依據。但圖(b)，安全系數變幅在0.1范圍內，實例間有足夠的相似性，其中投影值小于1.7的為一類，投影值在1.7-1.9的為二類，投影值大于1.9的為三類，聚類結果可作為指導邊坡穩定的判斷依據。

3 結 語

通過投影聚類分析邊坡穩定性，可依據最佳投影方向，通過確定影響邊坡穩定性因素的貢獻排序，來指導邊坡整治，從而達到快速提升邊坡的穩定性的目的。同時，對安全系數相接近的情況，可通過投影尋蹤聚類方法進一步進行等級分類分析。因此，安全系數法和投影尋蹤聚類方法相結合，可對邊坡的穩定性進行綜合評價。此外，投影尋蹤聚類方法適應于小樣本間的聚類分析，對于樣本數量過大時，聚類效果受樣本特異性干擾較大，聚類效果可能失真。因此建議，在投影尋蹤聚類分析時為保持樣本間具有足夠的相似。

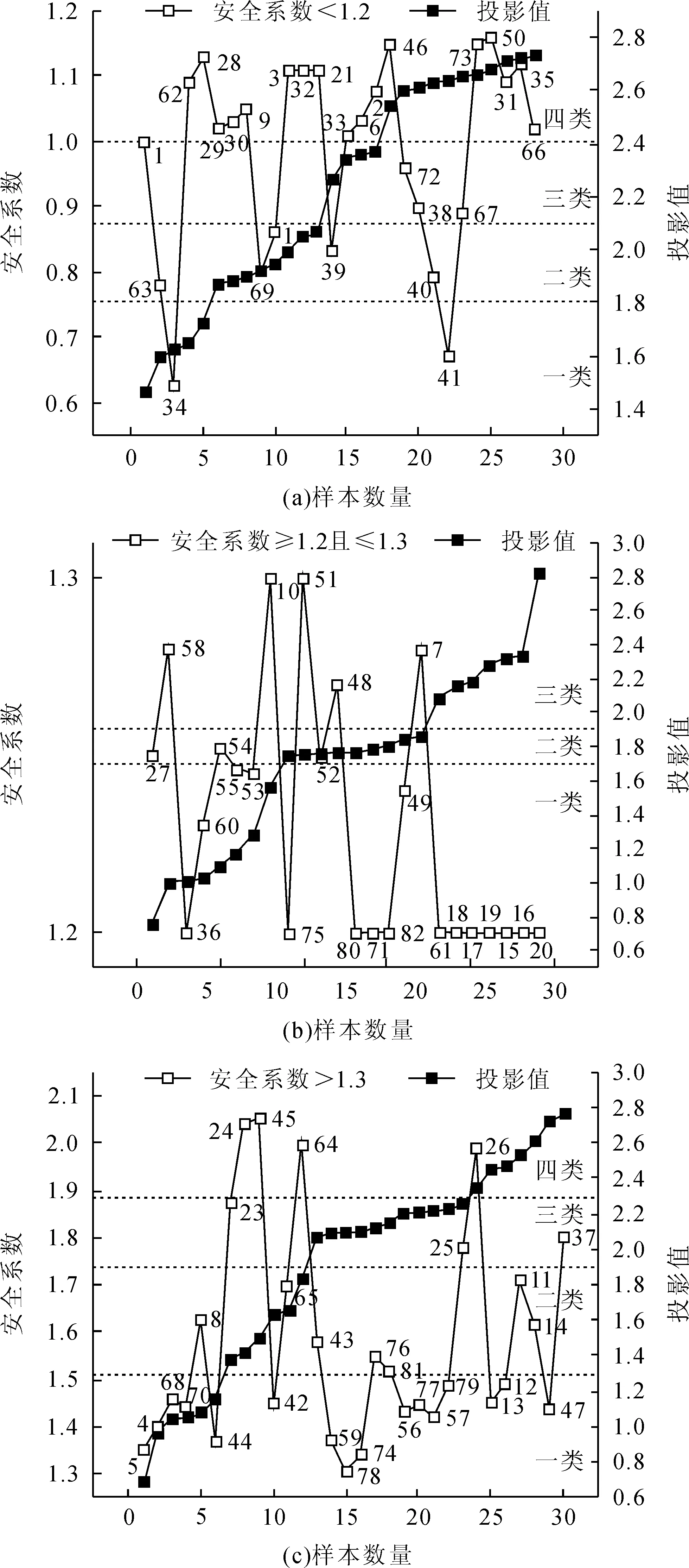
圖3 安全系數與投影尋蹤聚類值