咬文嚼字 明辨概率

范 斌

學習語文需要咬文嚼字，學習數學也需要咬文嚼字。概率問題，看上去好像很簡單，其實并非如此，如不細細審題，咬文嚼字，稍不留神，便會出錯。

例1甲、乙、丙三名同學站成一排進行畢業合影留念，求甲、乙兩人相鄰的概率。

【錯解】用樹狀圖分析如下：

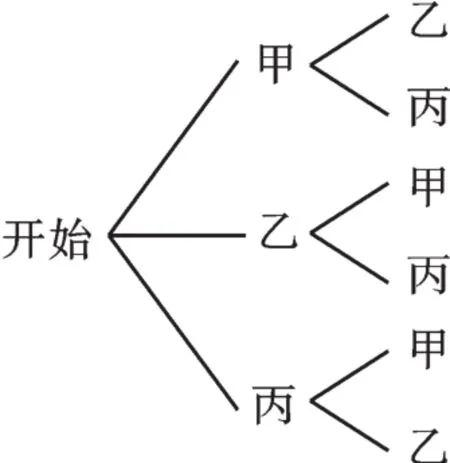
∵共有6種等可能的結果，甲、乙兩人相鄰有2種情況，∴P（甲、乙兩人相鄰）=

【分析】樹狀圖畫出了甲、乙、丙中兩人站的位置，留下的一個位置給剩下的第三人。當你完整列出三人站的位置圖時會發現，共有4種站法使甲、乙兩人相鄰。其實本題也可看成是三個層次的排序站位問題。

【正解】用樹狀圖分析如下：

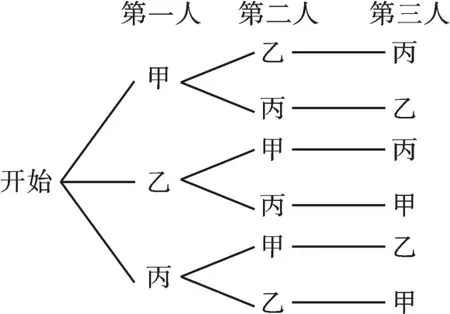
∵共有6種等可能的結果，其中甲、乙兩人恰好相鄰有4種情況，∴P（甲、乙兩人相鄰）

例2某校組織學生參觀航天展覽，甲、乙、丙、丁四位同學隨機分成兩組乘車。用列表法（或樹狀圖法）求甲、乙分在同一組的概率。

【錯解】根據題意畫樹狀圖如下：

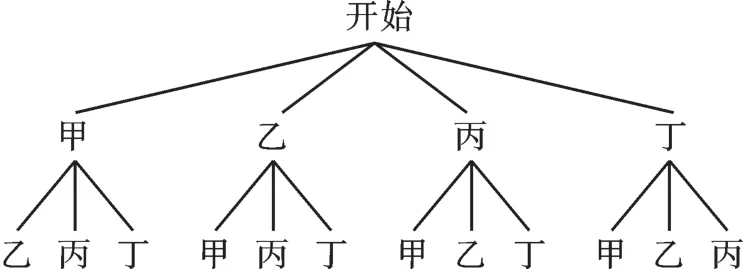
∵共有12種等可能的結果，甲、乙分在同一組的有2種情況，∴P（甲、乙分在同一組）=

【分析】當丙、丁，丁、丙在一組，也意味著甲、乙兩人在另一組，錯解恰恰遺漏了這種情況，導致錯誤。

【正解】根據題意畫樹狀圖如下：

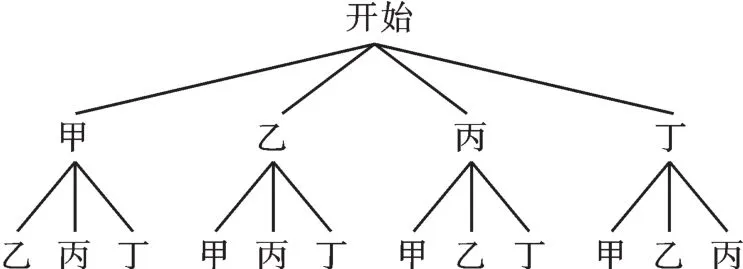
∵共有12種等可能的結果，其中甲、乙分在同一組的有4種情況，∴P（甲、乙分在同一組）

【點評】我們在用樹狀圖法求概率時，切不可畫出樹狀圖后便急不可待地忙于求概率，一定要咬文嚼字，仔細審題，讀懂題目中每一句的含義，小心謹慎地不重不漏地列出所有等可能的結果。