熵權法并聯組合模型在大壩變形監測中的應用

鄭旭東，陳天偉，鄧捷利，段青達，甘 若，王 雷

(1.桂林理工大學測繪地理信息學院，廣西桂林541004；2.廣西空間信息與測繪重點實驗室，廣西桂林541004)

0 引 言

目前，大壩變形預測的方法主要有BP神經網絡法、支持向量機法、相關向量機法、時間序列法等[1]。由于大壩工程的復雜性，以及外界條件的不確定性，決定了使用單一預測模型進行變形預測時，難以得到預測精度和預測期數都較為優秀的預測結果。針對大壩變形預測中存在的種種問題，部分學者進行了如下研究：王利等使用改進灰色模型在大壩沉降預測中取得相對誤差小于2%的預測結果[2]；何啟等使用改進的加權馬爾可夫鏈模型得到了平均相對誤差為0.71%的預測結果[3]；覃邵峰使用改進的ARIMA模型在大壩變形預測中平均相對誤差為0.48%[4]。為了能在實際預測中盡可能地發揮單一模型的預測優勢，又能約束各自的缺陷，本文基于信息熵原理提出熵權法并聯組合模型。使用灰色—加權馬爾可夫鏈預測模型用于解決變形預測中“少數據，貧信息”以及灰色模型預測周期短的問題，同時使用ARIMA模型來提高預測結果的精度，利用最大熵原理對兩模型合理組合，得到一個精度更高、更加合理的預測模型。

1 模型介紹

1.1 灰色—加權馬爾可夫鏈

1.1.1灰色預測模型GM(1.1)

灰色理論主要研究“小樣本，貧信息”的不確定系統的問題[5]。建立灰色模型時，為了淡化原始數據隨機性誤差的影響，首先對原始數據進行累加處理，再用微分方程進行建模，最后對模型值進行還原，得到預測值。由于該模型在其他文獻中出現較多，本文不再加以詳述。

1.1.2加權馬爾可夫鏈預測

對于一組隨機變量，在驗證其滿足“馬氏性”后，通過各步長的狀態轉移矩陣，以及其相對應的狀態做出預測后，利用其各階自相關系數能夠描述出各種滯時指標值相關關系的強弱這一特性[6]，對各步長的預測結果按照相依關系的強弱進行加權平均，這就是加權馬爾可夫鏈預測法的基本思想。

加權馬爾可夫鏈預測的步驟：

(2)“馬氏性”檢驗。

(3)計算各階自相關系數rk，k∈E

(1)

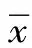
(2)

式中，wk為各個滯時(即步長)的馬爾可夫鏈的權重；m為預測的最大階數。

(4)根據步驟(1)所劃分的狀態，統計出各步長的狀態轉移概率矩陣。

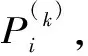
(6)將同一狀態的各預測概率加權求和作為該指標值處于該狀態的預測概率，即

(3)

則最終該指標值的預測狀態，即max{Pi，i∈E}。

(7)求出級別特征值對預測值進行估算[7]。待該指標值預測完成后，將預測值加入到原始序列中，重復步驟(1)～(7)即可完成對下一指標值的滾動預測。

1.1.3灰色—加權馬爾可夫鏈

灰色預測模型的優點是需要的數據信息較少，但其預測時間較短，而且對于波動性較大的數據，預測效果也不盡人意。而馬爾可夫鏈預測模型是通過統計原始序列得到狀態轉移概率矩陣進行預測，能夠在對變化較大的隨機序列的預測中取得不錯的效果，但其需要足夠多的原始數據來統計出原始序列的內在規律。故將兩模型進行串聯組合，用馬爾可夫鏈預測模型對灰色模型的結果進行改正，以提高預測精度。其具體步驟如下：

(1)將灰色模型的擬合值和實際觀測值進行對比，求出相對誤差。

(2)用求出的相對誤差進行馬爾可夫鏈建模，由馬爾可夫鏈預測模型預測出某時段的相對誤差。

(3)用馬爾可夫鏈預測模型預測出的相對誤差對灰色模型的預測值進行改正。

1.2 ARIMA模型

ARIMA模型也寫作為ARIMA(p，d，q)模型，它的實質是將ARIMA(p，q)進行d階差分得到的。通過這樣的操作，把一個非平穩的時間序列轉化成一個平穩的時間序列，再通過觀察相關函數結尾和拖尾特征得到自回歸階數p和移動平均階數q，對時間序列進行ARIMA建模，達到預測的效果[8]。ARIMA模型為

φ(B)(1-B)dYt=θ(B)et或
φ(B)dYt=θ(B)et

(4)

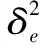
1.3 基于熵權法的組合模型

并聯組合模型的關鍵在于對單一模型的確定及單一模型權重的確定。本文采用熵權法確定各個單一模型權重，建立組合模型來預測大壩變形的數據。熵權法是根據評價對象的指標值構成的判斷矩陣來確定權重的一種方法。如果把信息熵理解為某種特定信息xi出現的概率p(xi)，那么信息熵H(x)的定義為

(5)

根據信息熵的定義可知，我們將特定信息認為是單項預測模型的誤差，如果單項模型的誤差的信息熵越小，其變異程度也就越大，則該單項預測模型的權重也越小。反之，模型誤差的信息越大，那么其變異程度越小，則模型的權重也就越大[9]。

因此，可以利用信息熵原理來確定單一模型的權重。具體步驟如下：

(1)計算單個模型對應時刻的相對誤差權重

(6)

式中，eij為第i個模型第j時刻的相對誤差。

(2)計算第i個模型相對誤差的熵值

(7)

式中，k=1/lnn，其中，n為選擇的單一模型數量。

(3)計算第i個模型相對誤差序列的變異程度系數

di=1-Hi

(8)

(4)計算第i個模型的權重系數

(9)

(5)將單一模型的預測值和求得的權重加權求和，獲得組合模型的預測值

(10)

式中，yi為單一模型的預測值。

組合預測模型建模基本流程如圖1所示。

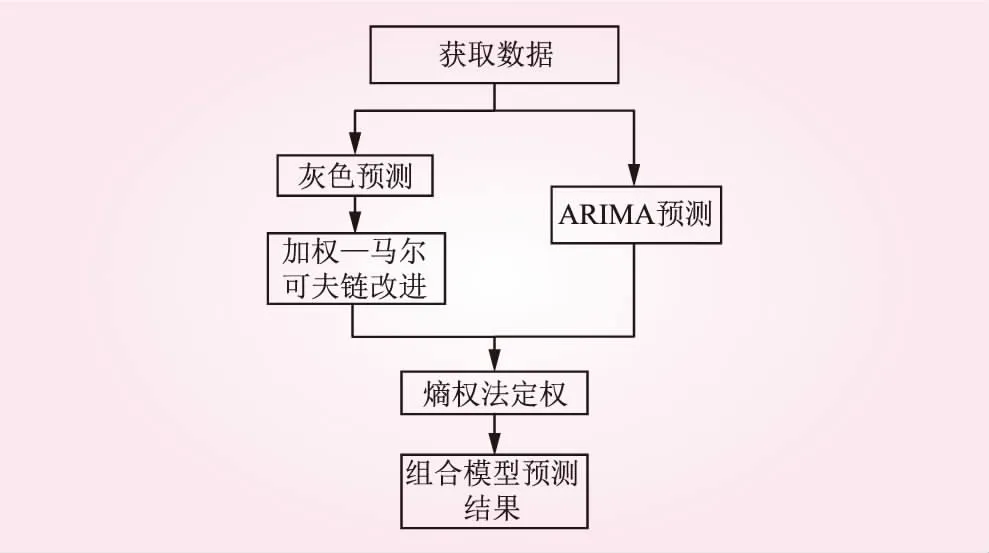
圖1 組合模型建模流程

表1 各模型預測值對比

2 具體實例

本文以某大壩水平變形監測點水平徑向位移觀測值為例，數據來源于文獻[2，10]。這里取前16期的觀測值作為原始起算數據，后4期數據和預測數據進行對比。觀測原始數據如圖2所示。

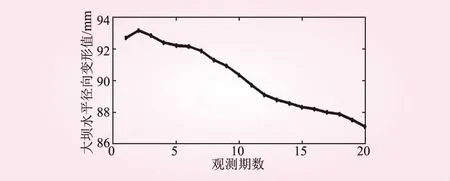
圖2 原始數據

2.1 單項模型預測

將灰色模型預測得到的前16期的擬合值與實際觀測值對比得到的相對誤差，對相對誤差進行馬氏性檢驗，用馬爾可夫鏈模型進行建模，預測得到后4期相對誤差，用此結果對灰色模型的預測值進行改進，即可得到灰色—加權馬爾可夫鏈預測模型的預測值；將前16期數據進行一階差分處理，對處理的數據進行自回歸系數與偏回歸系數分析，確定ARIMA(p，d，q)模型的參數。經分析，確定p=3，d=1，q=3。利用SPSS軟件進行ARIMA建模，獲得預測值。其結果見表1。

2.2 單項模型熵權計算

根據前文介紹的熵權計算公式以及兩個單一模型的變形值的預測結果，可得到灰色—加權馬爾可夫鏈預測模型，ARIMA預測模型在并聯組合模型中所占的權重分別為：ω1=0.75，ω2=0.25；再由式(10)求得最終大壩水平徑向位移的預測值Y={87.837，87.555，87.196，86.862}。

2.3 結果分析

為了更加直觀的表現出3種模型的預測效果，把3種模型的預測結果與實測值的對比用折線圖的形式表現，如圖3所示。

表中，模型一是指灰色—加權馬爾可夫鏈模型，模型二是指ARIMA模型，模型三是指基于熵權法的組合模型。

從表1、圖3分析相對誤差可得，組合模型預測效果最好，平均相對誤差約為-0.26%，其次為ARIMA預測模型，平均相對誤差約為0.27%；加權馬爾可夫鏈預測模型相對較差，平均相對誤差為0.46%。單就平均誤差而言，組合模型和ARIMA模型差別不大。為了進一步分析3種模型的平穩性以及精確度，按照整體評價預測方法的原則，引入以下評價

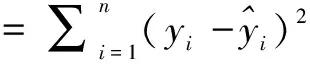
(10)

表3 預測結果對比

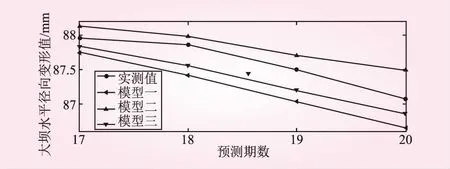
圖3 各模型預測值與真實值對比

(11)

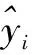
根據以上兩種評價指標，得出預測評價結果見表2。

表2 模型的評價指標對比

實例分析表明，組合模型的預測精度最好，與實際觀測數據相比較，Theil不等系數和誤差平方和均優于單一的預測模型，顯示出它在大壩變形預測精度上的優越性；其次，組合預測模型可以有效的彌補單一預測模型實際預測中存在的不足。對于現有的大壩變形預測模型而言，并聯加權模型可以合理的結合各單一模型的優點，提高預測結果精度。為避免其偶然性，筆者使用文獻[3]中的數據再次進行實驗，求得的模型一和模型二的權重為ω1=0.14，ω2=0.86。由于篇幅限制，在此只對結果進行呈現。其結果見表3、4。

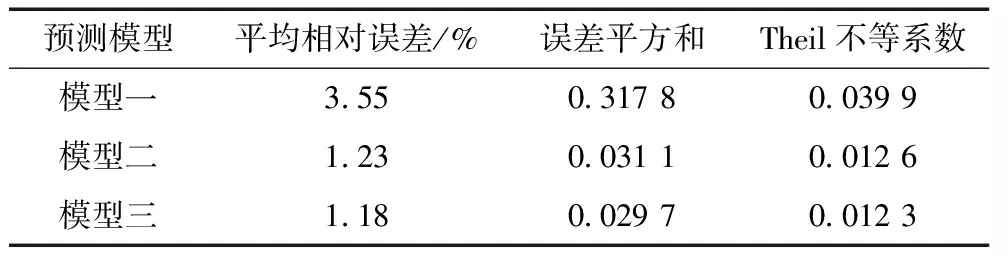
表4 預測結果精度指標對比

由表3、4結果可知，對文獻中的大壩水平位移分別進行灰色—加權馬爾可夫鏈模型，ARIMA模型和組合模型的預測，得到的預測結果從平均相對誤差，誤差平方和，以及Theil不等系數來看組合模型均為最優，由此可見基于熵權法的并聯組合模型對于大壩變形預測來說是一種行之有效的預測方法。

3 結 論

本文針對有限的觀測數據，結合灰色理論適用于“小樣本、貧信息”的特點；馬爾可夫鏈能夠準確擬合波動性較大的數據的特點；ARIMA模型能夠挖掘非平穩時間序列的內部信息，擬合出變化趨勢，從而實現預測目的，具有建模簡單的特點；并且結合最大熵的原理對模型進行合理的組合，建立了基于最大熵原理的混合預測模型，通過實例驗證了該模型對于小樣本序列預測精度較高。具體結論如下：

(1)基于信息熵原理，建立并聯組合模型來預測大壩的形變量，該方法在精度上較單一模型有所提高，并且平衡了單一模型的實測數據和樣本數據之間在質量和數量上的需求，同時能夠平衡各單一模型的擬合及預測精度以及普適性等方面的優點及缺點。

(2)基于信息熵原理，可對在真實值上下浮動的單一模型的預測值進行合理組合，減少了人為因素，使得組合模型在預測結果上更加接近真實值，從而提高了預測模型的預測精度以及合理性，為數據處理以及大壩變形預測提供了一條新的途經。