抽蓄電站地下廠房全廠溫濕度分布規律的數值計算研究

施 晨，胡代清，衣傳寶，劉玉成，許 昌，李林敏

(1.河海大學能源與電氣學院，江蘇南京211100；2.安徽金寨抽水蓄能有限公司，安徽六安237300；3.國網新源控股有限公司，北京100761)

0 引 言

隨著電網結構不斷復雜化、擾動的不斷多樣化，抽水蓄能電站作為電網電能品質的調節器，近年建設規模不斷擴大[1]。而隨著大型地下工程建設技術的成熟，抽水蓄能電站的設計建設逐漸傾向于采用地下廠房方案。這種布局不僅具有人防作用，同時能最大程度地保護電站建設區域的生態環境[2]。但由于電站深埋地下，電站與外界通風換熱途徑較為復雜，電站內易出現溫濕度分布不均勻和超標等熱濕環境問題，不僅影響機電設備的安全運行，同時也影響工作人員的身體健康與工作效率。

國內外學者針對水電站地下廠房溫濕度環境問題進行了大量研究工作。在理論計算方面，劉琳[3]結合射流理論對白鶴灘水電站地下廠房整體進風網絡進行風速等參量的計算確定了空氣處理方案；Tuve[4]采用射流理論對室內環境中的速度、溫度等重要參量的分布進行預測。在模型試驗上，何喆[5]對瑯琊山水電站地下廠房建立了相似模型，通過模型試驗的數據分析得出溫度、速度分布規律，為流場優化提供了參考；在數值計算上，丹麥科學家Nielsen等[6]于1974年首次將基于k-ε湍流模型的CFD計算方法對室內空氣流動進行了三維數值模擬，而在水電站地下廠房的數值計算上；董蕾[7]對厄瓜多爾科卡科多辛克雷水電站地下廠房發電機層的氣流組織進行了數值模擬及分析，并運用不同的評價指標確定了通風系統的最佳送風速度。當前針對地下廠房溫濕度的數值研究多集中于地下廠房單獨某層的溫濕度環境分析，而針對主廠房全廠的數值研究較為缺乏。

抽水蓄能電站的主廠房是電站運維的關鍵區域，該區域布置復雜，機電設備密集，散熱量巨大，運維人員往來頻繁，研究其環境溫濕度的分布規律具有重要意義，過去的研究主要采用針對部分區域的溫濕度問題進行測量和數值建模方面的研究，解決了部分問題，但是地下廠房的整體通風方式影響整體溫濕度、速度場分布，且相互影響，相關耦合性非常強。本文采用現場實測與數值模擬相結合的方法，對華東某抽水蓄能電站地下主廠房全廠區域進行數值建模，結合現場試驗數據對不同季節工況下的全廠熱濕環境進行數值模擬，分析不同工況下全廠各樓層的溫濕度分布規律，提出優化運行方案，為抽水蓄能電站廠房溫濕度環境控制與管理提供理論依據。

1 數學模型

1.1 通用控制方程

將流體動力學物理守恒定律中的質量守恒、動量守恒與能量守恒方程寫成通用形式如下[8]：

(1)

式中，φ為通用變量，可代表速度、溫度等變量；Γ為廣義擴散系數；S為廣義源項。式(1)從左往右的四項依次是非穩態項、對流項、擴散項和源項。

在地下廠房熱濕環境的計算中，相對濕度是一個重要的考察對象，本文使用組分輸運方程來計算相對濕度的輸運規律，令φ=cs，Γ=Dsρ，S=Ss，則式(1)可寫成：

(2)

式中，cs為組分s的體積濃度；Ds為組分s的擴散系數；Ss為組分s的產生率。

1.2 湍流模型

抽水蓄能電站地下廠房風口眾多，流動復雜，流動過程中具有不斷變化、隨機的湍流現象，本文采用標準k-ε湍流模型來計算[9，10]。其中湍流動能k與湍動能耗散率ε分別被定義為

(3)

(4)

式中，ρ是流體密度；i、j、k分別代表各坐標分量；ui、uj代表平均相對速度分量；μ為有效粘性系數。k和ε的輸運方程如下：

(5)

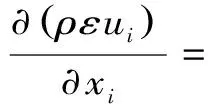
(6)

其中，Gk是由于平均速度梯度引起的湍動能源項，由下式計算：

(7)

而Gb是由于浮力引起的湍動能源項，對于不可壓縮流體，其值為0，而對于可壓縮流體，有：

(8)

式中，Prl是Prandtl數，在該模型中可取Prl=0.85；gi是重力加速度在i方向的分量；β為熱膨脹系數。YM代表可壓湍流中脈動擴張的貢獻，對于不可壓流體，YM=0。模型常數C1ε、C2ε、Cμ、σk、σε的取值分別為[11]C1ε=1.44，C2ε=1.92，Cμ=0.09，σk=1.0，σε=1.22。

2 物理模型

2.1 模型與網格劃分

華東某抽水蓄能電站主廠房共分4層，自上而下依次為發電機層、中間層、水輪機層以及蝸殼層。發電機層在靠近進廠交通洞區域設有安裝間，面積略大，發電機層尺寸為140.3 m×20.00 m(長×寬)，其余3層尺寸均為120.2 m×20.00 m(長×寬)，主廠房總高37.8 m，4層凈高自上而下依次為17.7、5.25、5.95、6.65 m。

主廠房進風來源共有3條途徑：①交通洞→9號洞→3號洞→主廠房安裝間頂部空調；②通風兼安全洞→端副廠房頂部空調；③交通洞→9號洞→水輪機層進風口。主廠房頂部共有46個進風口，4臺組合式空調機組，層間夾墻風口共有44個。新風從主廠房頂部進入，通過層間風口聯通，最終從中間層下游側排向母線洞，主廠房空氣循環見圖1。

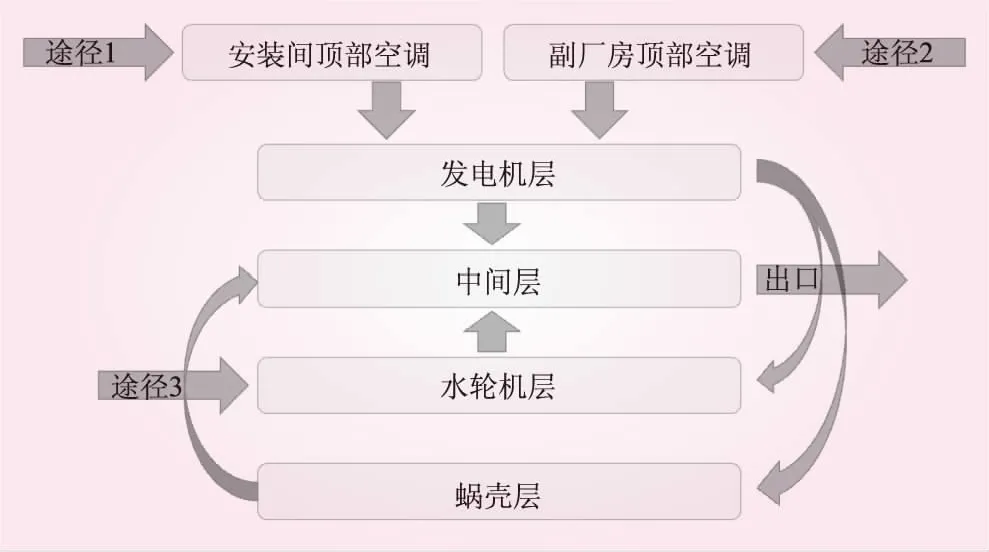
圖1 主廠房空氣循環示意

對主廠房的通風網絡以及三維立體結構以1∶1的比例進行建模，并對其進行網格劃分，所建立的三維幾何模型如圖2所示。

圖2 主廠房幾何模型

表1 進口邊界條件

為方便研究，根據實際情況對模型進行簡化：①簡化主廠房發電機層頂棚弧形結構以及頂部橋機等繁瑣物件，主廠房內球閥、管道等非主要物件省略或以規則實體等提及替代。②由于空調送風管道采用雙層保溫材料，將空調機組至送風口管道省略，近似認為空調出口送風參數等于送風口送風參數。③省略主廠房壁面中層間通風管道以及軸流風機，僅保留風口，以風口對應的現場測試數據作為計算的邊界條件。

2.2 邊界條件與數值細節

電站主廠房頂端途徑①與②進風口處各有2臺組合式空調機組，且兩側各運行1臺，備用1臺，途徑③處設置風機。本文計算春、夏兩種工況，分別以2017年3月20日與7月15日現場測試的溫濕度、壁溫數據以及文獻[12]中的熱源散熱量作為參考數據，以確定邊界條件。各進風途徑風速分別由各自風機進風量換算得出，途徑③溫濕度為直接測量數據，空調處理后的空氣焓值由下式給出[13]：

(9)

式中，Q為空調制冷量；ma為空氣質量流量，兩者均可由空調銘牌得出；h1為初態比焓；h2為終態比焓，最終溫濕度參數由h2查詢焓濕圖得到。兩種工況下各進口邊界條件設置如表1所示。除主廠房頂部46個風口向主廠房發電機層的射流送風外，發電機層通過上下游側壁面處的夾墻風管向下面3層送風形成循環，本文簡化風管建模，僅保留風口，對應的送風風口分別為速度進口(volecity-inlet)與速度出口(volecity-outlet)，具體數值根據現場測試數據確定。最終出口為中間層下游側的回風口，邊界條件為壓力出口(pressure-outlet)。

壓力-速度耦合采用Simple算法，湍流模型采用k-ε雙方程模型，由于涉及組分以及傳熱計算，開啟組分方程以及能量方程，同時采用DO輻射模型[14，15]，重力加速度g=9.8 m/s2。本文計算采用FLUENT求解器求解。

3 計算結果分析與優化方案論證

3.1 模型可靠性驗證

在現場測試時，針對主廠房4層共布置了20個測量點，每層測點5個，其中發電機層熱源較少，不布置測點。測量數據時采用手持溫濕度監測設備，測點高度均為1.7 m。各層測點在水平方向上的分布如圖3所示。

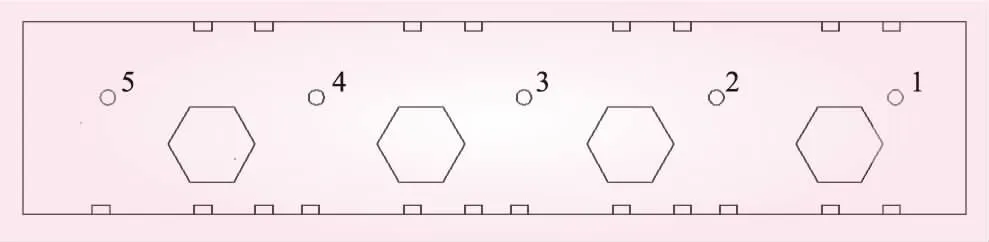
圖3 各層測點示意

以春季工況為例，將2017年3月20日的各層實測值分別取平均值，與對應位置處1.7 m高度處的計算值對比，如圖4所示。

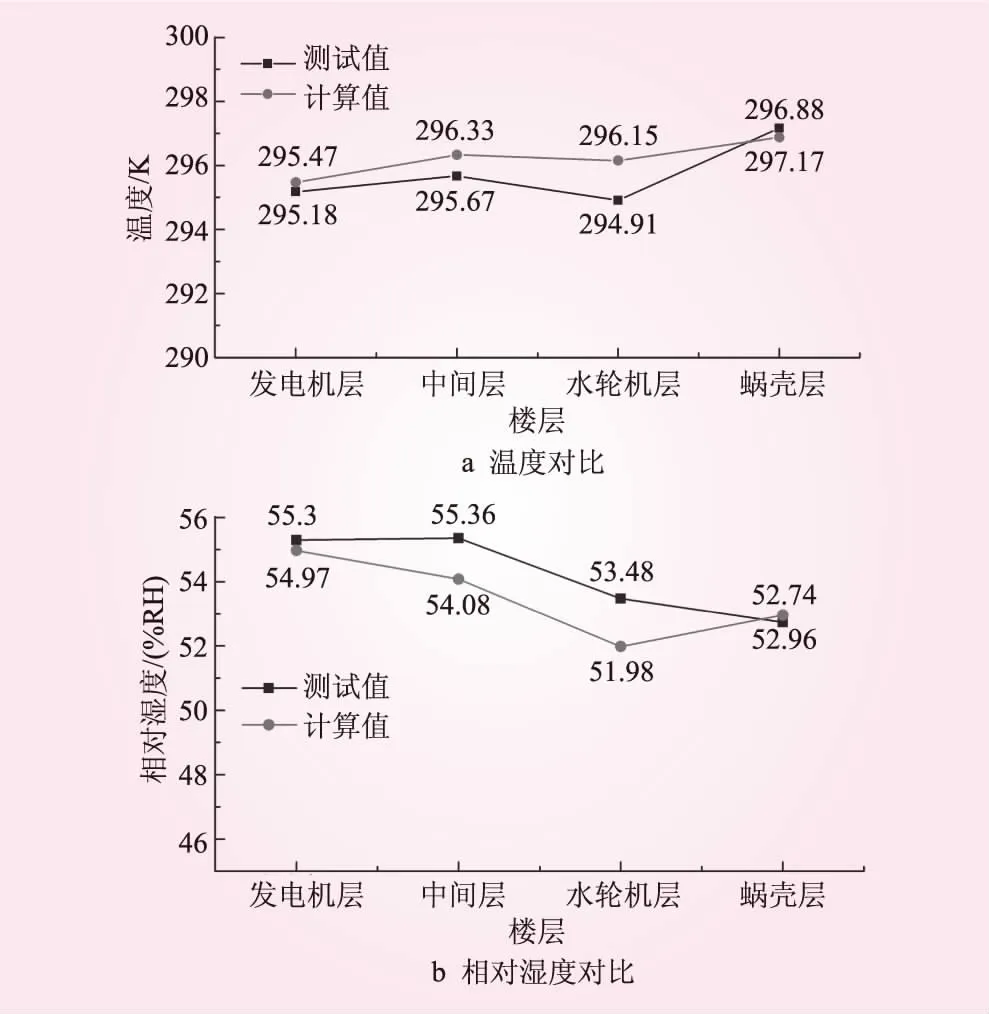
圖4 可靠性驗證

由圖4可知，各層溫度和濕度的實測值與計算值總體吻合。經過計算，各層溫度計算值與實測值平均誤差為0.5 K，最大誤差1.24 K，最小誤差0.29 K。相對濕度計算值與實測值平均誤差0.67%，最大及最小誤差分別為1.50%和0.22%。

3.2 計算結果分析

圖5 春季與夏季工況的溫濕度計算結果

根據春季、夏季兩種工況的計算結果，分別截取y=3.65 m豎直截面處2種工況下的溫度與相對濕度云圖，結果如圖5所示。根據計算結果可以看出，在春夏2種工況下，發電機層的溫度在全廠中均為最低，其余3層溫度相對較高。且由于所選取截面頂部進風途徑①下游側空調運行，另一端的進風途徑②下游側空調處于備用狀態，未開啟運行，在發電機層左側區域看到自上而下的射流組織，且出現溫度較低的低溫區，溫度分布不均。在4層空間中發電機層電氣設備散熱量最大，但發電機層空間范圍最大且直接接受頂部低溫射流送風，使該層溫度降低。而下3層空間較小且均利用發電機層氣流進行通風，通風效果不佳。發電機層氣流存在不均勻性，這主要由于發電機層的安裝間范圍較大且不存在熱源，發電機層熱源集中在機組附近，熱源分布不均。相對濕度上，2個工況的發電機層頂部射流送風口相對濕度較高，這是由于氣流經過空調處理后溫度降低，空氣中水分迅速達到露點溫度并隨著溫度降低不斷下降，從而達到降低濕度的目的。含濕量得到降低的氣流離開空調之后幾乎以100%的相對濕度進入溫度較高的發電機層，與發電機層內的熱空氣混合后，溫度迅速升高，相對濕度迅速降低。

兩種工況所不同的是：溫度上，主廠房整體區域夏季高于春季，但均能低于302.2 K；濕度上，水輪機層夏季明顯高于春季，且部分情況下高于75%，對機電設備安全運行形成一定威脅，也影響運維人員的人體舒適度。這是因為，水輪機層進風途徑③引進主廠房的新風相對濕度接近100%，而溫度與水輪機層環境溫度幾乎沒有差異，新風含濕量較高，造成了水輪機層相對濕度較高。除此之外，因熱空氣會因自然對流而上升，水輪機層的濕空氣通過樓梯口進入中間層，一定程度上造成了中間層部分區域相對濕度的升高。

3.3 優化方案計算及論證

目前電站的運行過程中，出現了相對濕度過高的問題，為提升機電設備檢修環境與運維人員的人體舒適度，提出以下優化運行方案：假定在水輪機層進風途徑③處加設組合式空調機組，根據式(9)以及焓濕圖進行計算，假定選型為申菱40HP的LD130型號組合式空調機組，優化前后途徑③進風參數如表2所示。

表2 優化前后途徑③進風參數

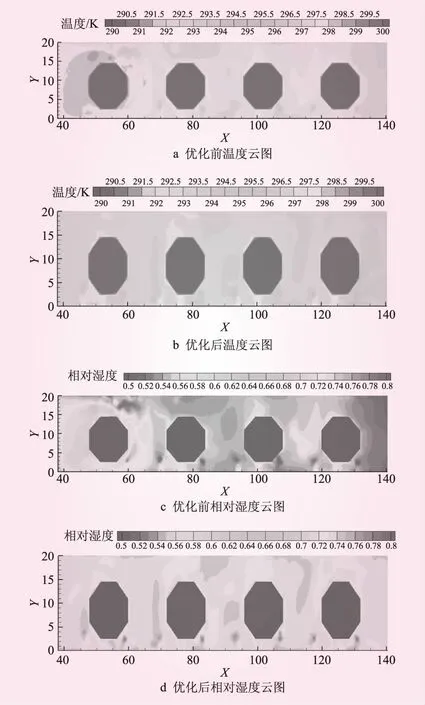
圖6 優化前后溫濕度環境對比

其余送風參數與夏季工況下的參數一致，截取水輪機層相對高度zr=1.7 m處的水平截面的溫濕度云圖進行分析，其結果如圖6所示。由計算結果可得，優化前，由于水輪機的發熱及其與周圍空氣的換熱導致水輪機周圍溫度較高，溫度分布不均勻，原空調系統對該層空氣的冷卻效果不明顯。優化后，水輪機層溫度有所下降，且溫度分布更加均勻。且水輪機層送風溫度的降低，使其與上下層之間溫度差降低，優化后樓梯口的溫度均勻性優于優化之前。優化后水輪機層環境溫度下降，有利于機電設備的安全運行。另一方面，水輪機層相對濕度在優化前存在超標的情況，圖6c中大部分區域相對濕度達到了80%。優化后，相對濕度得到了有效降低，如圖6d所示，大部分區域相對濕度在74%以內。可見，優化措施對于控制水輪機層的空氣濕度具有較好的效果。

4 結 論

本文建立了基于CFD的抽水蓄能電站地下主廠房全廠溫濕度、速度場的數值計算模型，通過試驗數據驗證了模型的可靠性，分析了全廠溫濕度和速度的分布特性。針對運行過程中，水輪機層濕度過高的問題，提出在進風口加設組合式空調機組除濕的方案。通過數值計算，在夏季工況下，水輪機層大部分區域相對濕度從最高80%下降到74%以內，而且通風效果明顯提升，優化效果較明顯。