爆炸煙云擴散的時空分布模型及特性*

段中山，過惠平，馮孝杰，羅昆升，袁 偉

（1.火箭軍工程大學核工程學院，陜西 西安 710025；2.陸軍勤務學院，重慶 401331；3.火箭軍研究院，北京 100085）

炸藥爆炸后的煙云擴散是常見的物理現象[1]。對炸藥爆炸的研究，往往偏重于炸藥的性能、威力和毀傷效應，大多只關注炸藥爆轟參數及火球膨脹尺度。事實上，深入開展爆炸煙云擴散規律的研究不僅可以反演炸藥爆炸當量、威力、爆炸火球大小等信息，實現戰場爆炸或事故爆炸偵測，而且還能推測炸藥所驅動的污染物的擴散信息，預測煙云高度、體積以及污染物含量等源項參數。總之，開展煙云時空分布規律的研究對戰場爆炸偵測、臟彈襲擊與核武器化學爆炸事故源項反演、后果評價以及常規爆炸事故污染物擴散評估等都有重要意義。

鄭毅等[2]采用氣象模式對中尺度煙云擴散進行了數值模擬，沒有對小尺度煙云進行討論，也沒有建立擴散模型。李曉麗等[3]開展了爆炸煙云實驗和變密度法數值模擬，但實驗測得的煙云邊界模糊且時間過短（僅15 s），數值計算模型過于簡化。王善強等[4]分析了臟彈煙云擴散特性，認為經驗公式適用范圍有限。Makhviladze 等[5]、Kansa 等[6]、Kanarska 等[7]及Mishra 等[8]都開展過浮力煙團相關理論研究，大多屬純理論計算，沒有建立具體的通用模型。近年由于臟彈襲擊風險增大，Thielen 等[9]、Sharon 等[10]及Leblel 等[11]進行了少量的爆炸實驗以尋找煙云擴散相關規律，并根據實驗結果提出了一些擬合模型，有關這些實驗的具體細節報道較少，實驗過程沒有嚴格限定煙云擴散條件，也沒有通過擴散機理分析和理論模型計算加以討論。目前爆炸煙云污染評估都是直接采用Church 經驗公式H=93M0.25來計算煙云的最終高度，但Church 公式不能描述煙云在擴散過程中的時空分布[12]。事實上Church 公式主要由53 kg TNT 以上炸藥爆炸及核爆炸的實驗結果擬合得到，沒有考慮爆炸條件本身的差異和外在氣象因素的影響，擬合的冪函數系數過大、冪次過小，后期大量實驗顯示該公式對小于100 kg TNT 的小尺度爆炸煙云爆高計算誤差較大[9-10]。

綜上所述，目前通過實驗或數值模擬開展的煙云擴散規律的研究各存利弊，因此本文中擬開展多組不同條件下爆炸煙云實驗，并結合數值模擬對爆炸煙云擴散模型及其特性進行系統研究，分析煙云的擴散機理，尋找擴散參數的變化規律，以期建立不同條件下爆炸煙云擴散通用模型。

1 爆炸煙云擴散時空分布理論與實驗

1.1 煙云擴散模型的物理描述

根據SCM(source characterization model)[13]，高能炸藥的爆炸過程可以劃分為爆轟、浮力煙團上升、大氣散布3 個階段，具體如圖1 所示。

第1 階段是炸藥爆轟階段。高溫、高壓的爆轟產物瞬間迅速向周圍膨脹，使得爆轟瞬間所達到的溫度、壓力不斷下降，當壓力下降到空氣壓力p0時，由于慣性效應，爆轟產物還要過度膨脹，直到速度基本為零[1]，此時爆炸產物密度遠低于空氣密度。該過程非常復雜，與炸藥種類、裝置構型、地表狀況、起爆方式等因素相關，對該過程開展精準研究非常困難[10]。煙云膨脹到最大時刻將形成一個固定形態與體積、低密度、高溫、氣體產物為主（含一定顆粒物）、有較小翻滾上升速度的初始煙團，本文擬采用實驗與經驗公式計算相結合的方法確定初始煙云參數。

第2 階段是爆炸煙云擴散上升的過程，該階段煙云擴散速度先升高后降低，擴散過程是一個復雜的流場動力學問題。此煙云抬升過程包含2 個亞階段：(1)煙云克服重力和上升阻力進行熱抬升加速運動的階段，持續幾秒到十幾秒，這一階段往往還伴隨少量后續燃燒化學反應；(2)熱抬升結束后的減速階段，該過程持續幾十秒到上百秒。整個第2 階段空氣不斷進入煙團，煙團密度增大、溫度降低，此時影響煙云時空分布的因素除煙云本身的體積、形態、密度、溫度、粒子攜帶外，外在因素主要是風和大氣穩定度。煙云擴散的理想狀態如圖2 所示，煙云最終將趨于穩定狀態后不再上升。

第3 階段為大氣擴散階段，煙云穩定后將在大氣風場作用下沉降至下游區域。

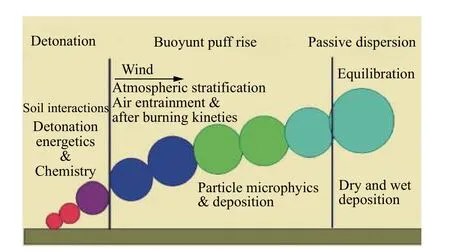
圖 1 SCM 模型[13]Fig.1 Source characterization model[13]

圖 2 理想煙云擴散示意圖[2]Fig.2 Schematic diagram of the ideal cloud spread[2]

1.2 爆炸煙云擴散實驗過程

本實驗屬于大型外場爆炸煙云擴散實驗，先后開展了不同TNT 當量M（1、16、62 kg）、不同地面條件（硬質地面和厚水泥地面）、不同殼體束縛（裸裝藥和厚殼體）的重復實驗，具體實驗概況如圖3 所示。實驗條件的變化是爆炸煙云擴散實驗成敗的關鍵[10]，因此，本實驗中均嚴格限定實驗條件，以便能夠得到可靠的實驗數據，具體實驗分組情況見表1，表1 中T0為空氣溫度，φ 為空氣的相對濕度。

首先設計了1、16、62 kg 級的TNT 炸藥化學爆炸裝置，為盡可能長時間記錄煙云，在實驗爆炸裝置里均勻布置了少量可示蹤煙云的發煙劑；然后選取實驗條件理想的時刻起爆裝置，同時記錄爆炸煙團的初始形態及其演變過程中的動態圖片和視頻；最后根據視場標定結果，使用便攜式計算機及其安裝的專業像素分析計算軟件對實驗所得視頻及圖片信息進行計算，得到了爆炸煙云擴散的時空分布數據。

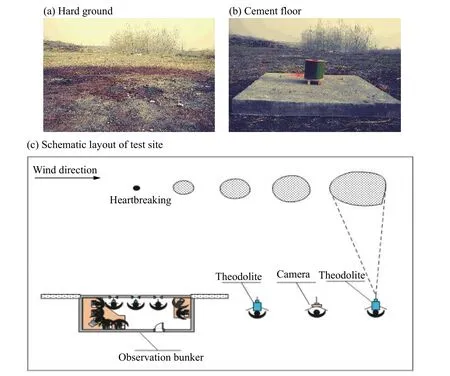
圖 3 外場實驗Fig.3 Outfield experiment

表 1 實驗分組Table 1 Experiment groups

2 爆炸煙云擴散理論方程與仿真模擬方法

2.1 煙云擴散流體動力學方程

由煙云浮力擴散機理及SCM[13]可知，炸藥爆炸后生成大量高溫低密度煙云，煙云主要受重力、上升阻力和大氣密度差帶來的浮力等影響，巨大的浮力是煙云運動的動力來源，煙云在浮力作用下快速上升，同時空氣進入、密度變大、溫度降低，爆炸煙云在擴散過程中遵循質量、動量和能量守恒方程。質量守恒方程一般形式:

式中：ρ 為密度；ui為i 方向上的速度；Sm可以為其他的自定義源項，本文中定義爆炸后的低密度煙團為流場源項。在慣性(非加速)坐標系中各方向遵守動量守恒方程，以i 方向為例:

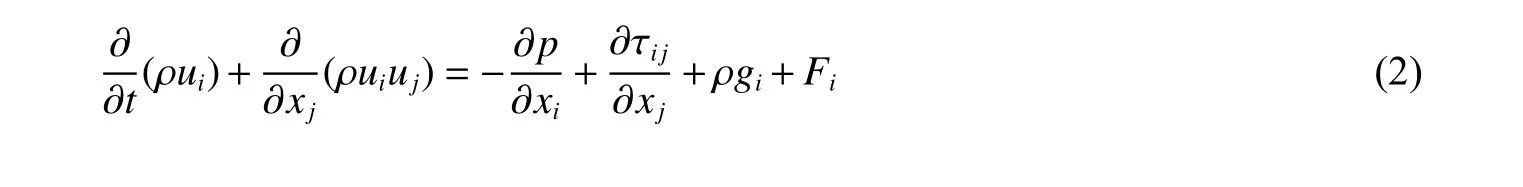
式中：p 為靜壓，tij為應力張量，gi和Fi分別為i 方向上的重力體積力和外部體積力；Fi包含了其他的模型相關源項，如多孔介質和自定義源項。煙團熱量的交換遵循能量守恒傳遞方程：

式中：E 為流體微團的總能量，包含內能、動能和勢能；hj′為組分j′的焓；keff為有效熱傳導系數；Jj′為組分j′的擴散通量。方程(3)等號右邊的前3 項分別描述熱傳導、組分擴散和黏性耗散帶來的能量輸運，Sh包括了化學反應熱以及其他體積熱源項。

2.2 煙云擴散時空分布建模方法與計算

根據煙云擴散機理可選用計算流體力學(computational fluid dynamics, CFD)方法對模型簡化后進行計算。本文將初始煙團簡化為橢球形、大小規整、密度溫度均勻、有一定初始速度、無粒子攜帶，不考慮拋灑、后續燃燒化學反應的理想煙團模型[14-15]，段中山等[16]對簡化模型的計算結果進行了實驗驗證，證明該簡化方法雖然不能完全仿真復雜煙云的擴散過程，但表征煙云基本時空分布、獲取流場基本信息等比較可靠。計算在ANSYS/Fluent 軟件中編定高溫低密度源項，實驗測量和理論公式相結合可得半徑r=1.93M0.32/(T/3 600)1/3，M 為炸藥當量，T 為爆溫(2 588 ℃)，由于受地面影響火球近似呈半橢球形態，確定1、16、62 kg TNT 的橢球煙團水平直徑約為4.17、10.12、15.61 m，垂直高度約3.13、7.59、11.71 m。假設火球膨脹后的壓力與空氣壓力基本相當或略低于空氣壓力，由ρ1=ρ0(T0/T)，其中ρ1為煙團密度，ρ0、T0分別為空氣密度和溫度，可得煙團密度為0.08～0.12 kg/m3，煙團的組成按照TNT 化學爆炸式中氣體產物體積分數設定，考慮到溫度迅速下降，將初始煙團均值溫度設為727 ℃，且煙團具有約5 m/s 的初始翻滾上升速度[17-20]。

本文中網格劃分采用Gambit 軟件完成，網格從中間到兩邊、從下到上采取1.02 倍遞增的步進劃分方式，生成的網格中間和下部網格密集以便更好地關注煙云擴散區域；設置左邊為inflow、右邊為outflow、底部邊界選取為wall；計算中合理設置混合物耦合計算模型、湍流模式、可壓縮流動、隨時間變化的非定常流；重力加速度為9.8 m/s2，空氣溫度為25 ℃；對x 向和y 向速度、能量、各物相體積分數及動能能量等進行收斂設定和殘差監視，殘差線下行且收斂較容易，能達到計算精度要求[21]。

3 研究結果及討論

3.1 爆炸煙云擴散機理

圖 4 實驗得到的煙云時空分布Fig.4 Experimental spatial and temporal distribution of the cloud

圖 5 模擬得到的煙云時空分布Fig.5 Simulated spatial and temporal distribution of the cloud

煙云擴散的基本情況如圖4～5 所示，實驗結果和模擬結果均顯示煙團橫截面呈蘑菇云形態。圖4整體較好地記錄了煙云的運動過程，但無法得到流場的具體信息。圖5 模擬結果則顯示，對于一個最初是橢球或是圓球的煙團，由于反向水平密度梯度作用而產生了大尺度、反旋轉、束狀渦流，它明顯地改變了氣團由傳統的高斯型濃度分布所描述的形狀，變成由2 個反漩渦環流組成的渦流結構，渦環圍繞其渦核由內向外翻卷，渦環直徑逐漸變大并且非常穩定地上升。CFD 方法獲得的煙云形態仿真結果與實驗觀測現象吻合，證明了煙云擴散機理是低密度高溫煙團在空氣浮力驅動下上升和擴散。

3.2 爆炸煙云擴散的時空分布

3.2.1 煙云頂部高度的變化

第1 組實驗主要為獲取大氣穩定、無風、厚水泥地面、裸裝藥條件下理想煙云的擴散模型。在有限實驗條件下，煙云擴散的不確定性因素多，難以保證實驗條件無干擾和實驗數據可靠，所以采取實驗與理論計算相互驗證的方法來開展研究。圖6 顯示煙云高度隨時間變化的實驗結果與理論計算數據相關性強、變化規律基本一致。理論計算結果比實驗值略高，這是因為爆炸后的真實煙團擴散非常復雜，伴有拋灑和后續燃燒化學反應，還可能存在較小的風場干擾，而簡化后的理想模型初始條件的設置上也存在可進一步優化的地方，所以兩者存在一定的偏差。結果表明：(1)實驗中獲取的煙云擴散時空分布數據整體規律性較強，數據可靠；(2)基于低密度高溫煙團擴散機理的建模計算方法能較好地表征煙云高度的變化。

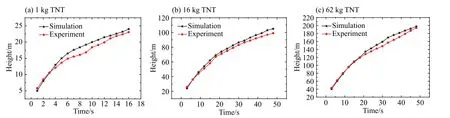
圖 6 不同當量的TNT 爆炸煙云高度隨時間的變化Fig.6 Heights varying with time for explosion clouds of TNT explosives having different weights

從圖6 可見，煙云擴散呈現先加速、后減速、最后幾乎不再上升的物理過程。進一步觀察煙云高度隨時間的變化曲線，發現煙云高度幾乎都是呈現冪函數規律上升，符合浮力加速、空氣阻力和重力減速的物理模型。采用Matlab 冪函數數學模型H(t)=atb對煙云高度變化規律進行擬合，擬合結果和擬合度R 如表2 所示。擬合結果顯示b=0.5±0.05 相對固定，而a 值隨炸藥量的增加而增大。令t=1 s，a=H(1)，H(1)也就是爆炸火球成型且翻滾總共1 s 時的煙云高度。火球膨脹到最大所需時間不到1 s，也就是說火球形成大小和1 s 上升高度共同決定H(1)，a 的下限值為2r=3.86M0.32/ (T/3 600)1/3，但是煙云在1 s 時刻由于拋灑和翻滾均大于2r，實驗和計算都顯示a=(6.1±1)M(0.32±0.03)。由于爆炸當量的不同，煙云到達穩定狀態的時間肯定也不同，Church 在描述煙云最大高度時只假設煙云2 min 到頂部，沒有具體時間模型[12]。實驗煙云后期視野模糊難以通過使用完全確定煙云上升的最終高度和時間，結合仿真計算共同確定1、16、62 kg TNT 爆炸煙云抬升至穩定狀態所需的時間tmax分別為30、70、110 s，抬升時間tmax與當量M 的擬合關系為：tmax=(28± 1.1)M(0.33±0.04)。

綜上所述，大氣穩定、無風、厚水泥地面、裸裝藥條件下，理想煙云擴散高度隨時間變化的模型為：H(t)= (6.1±1)M(0.32±0.03)t(0.5±0.05)，在tmax= (28±1.1)M(0.33±0.04)時刻煙云到達頂高。通過煙云高度分布模型和最大上升時間確定1、16、62 kg TNT 爆炸煙云的最終高度約36、125、240 m。Church 實驗在鋼板上進行，8 m/s 風速下53.52 kg TNT 爆炸煙云高度約220 m，實驗結果符合上述擬合模型[12]。

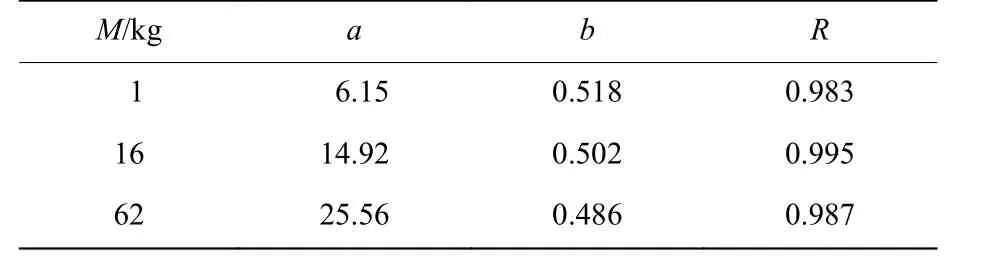
表 2 煙云高度擬合參數Table 2 Parameters of cloud height fit

3.2.2 煙云寬度和溫度的變化

煙云的寬度是計算煙云擴散體積變化的重要依據，Church 只給出了煙云寬度是其高度的0.4 倍的模糊結論[12]，本文實驗則顯示煙云寬度的變化與爆炸條件關系較大，爆炸環境的差異性使得煙云寬度差距較大，但可以確定的是煙云寬度與其高度不是簡單的比例關系。62 kg TNT 爆炸實驗中得到的煙云寬度變化如圖7 所示，對該煙云寬度進行D=atb+c 擬合，得到D=4.5t0.77+4.57，b 值較接近1，煙云寬度隨時間近乎呈線性規律增大，這與李曉麗等[3]在煙云擴散實驗中觀察到的一致。煙云溫度云圖也非常復雜，選取煙云中最高溫度的變化值擬合后如圖8 所示，發現溫度隨時間快速單調遞減，直到無限逼近常溫，溫度變化近似Tmax=a/t+b 反比例函數規律，a 的取值與炸藥爆炸后初始煙云溫度相關，b 的取值圍繞環境溫度變化。由反函數性質可以發現，煙云熱抬升時間總是在幾秒到十幾秒，該結果與已獲得的紅外熱成像實驗結果[16]相符。

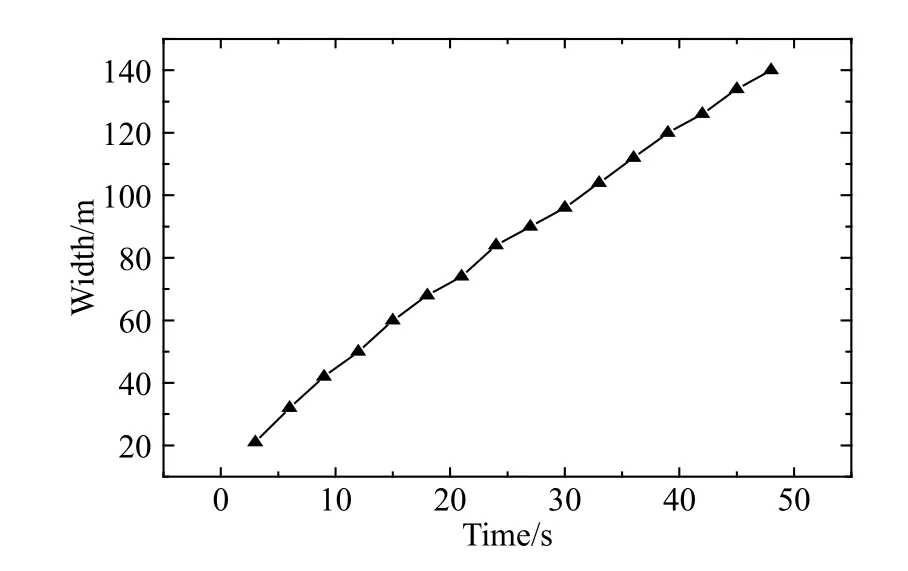
圖 7 煙云寬度增長規律Fig.7 Growth law of cloud width

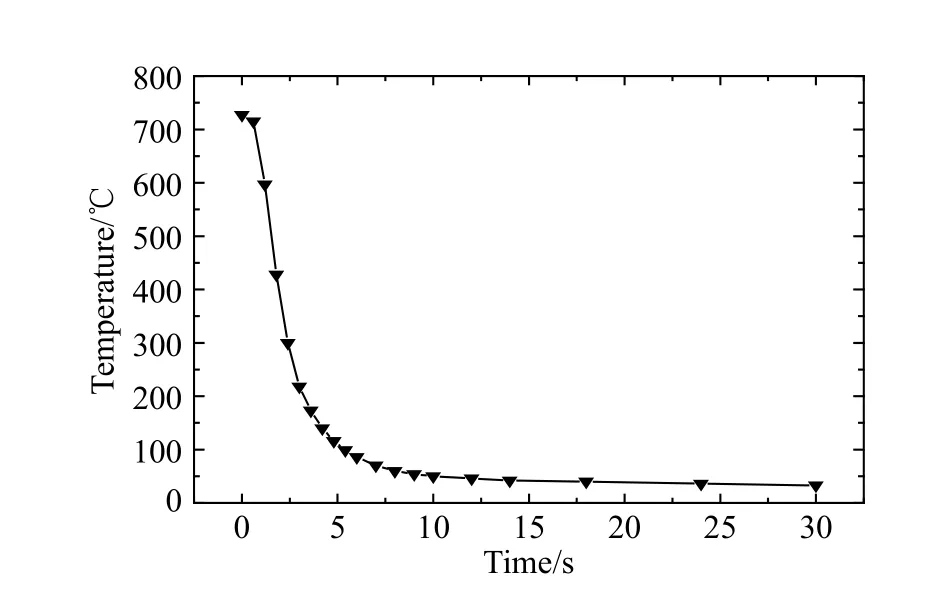
圖 8 煙云頂溫衰減規律Fig.8 Attenuation law of cloud top temperature

3.3 硬質地面和厚殼體束縛條件下煙云高度模型及特性

第2 組實驗為泥土硬質地面爆炸煙云擴散實驗，第1、2 組實驗結果的對比如圖9 所示，硬質地面爆炸煙云高度比水泥地面煙云高度低(5～20)%，證明硬質地面成坑與土壤顆粒物夾帶影響煙云上升，同時說明建立煙云擴散模型必須嚴格限定實驗條件。泥土硬質地面爆炸形成土坑要消耗一定的爆炸能量，使得同等TNT 當量下炸藥驅動能變小；且土坑中的泥土進入煙云，導致煙云整體密度變大、體積變小，這些原因使得煙云的上升高度降低。該條件下的實驗數據也顯示出煙云的擴散高度隨時間呈指數規律上升，可通過調整模型的a 值和b 值以獲得地面成坑條件下的煙云擴散模型，實驗數據擬合模型為H(t)=(6.3±1)M(0.29±0.03)t(0.5±0.05)。Thielen 等[9]開展的爆炸煙云實驗的實驗條件未見報道，但是從實驗結果分析來看，應該為硬質地面條件，而Sharon 等[10]報道的圖片顯示其開展的爆炸煙云實驗均在泥土地面上進行，其實驗煙云高度與水泥地模型計算高度相比要低，兩者實驗條件和實驗數據擬合均符合本文第2 組實驗的擬合模型。

圖 9 不同地面條件下爆炸煙云高度隨時間的變化Fig.9 Explosion cloud height varying with time under different ground conditions

針對爆炸裝置殼體對爆炸煙云高度的影響，僅開展了1 組裸裝藥和厚殼體束縛裝置TNT 爆炸煙云擴散對比實驗。結果顯示，采用厚殼體束縛爆炸裝置時，同等時刻爆炸煙云高度整體偏低。這是因為炸藥爆炸在拋撒殼體中會損失部分能量，同時殼體束縛會導致初始煙云體積變小、密度變大。具體殼體厚度與煙云擴散高度的定量關系還需設計更多實驗加以確定。炸藥種類、殼體束縛、風場變化、地面成坑等對煙云擴散都有影響，模型在不同條件下使用時，參數a、b 的值應隨之調整。本文中在不同實驗條件下構建的爆炸煙云高度模型在計算當量低于100 kg TNT 的爆炸煙云擴散高度時有一定的通用性。

4 結 語

（1）本文中開展的煙云時空分布實驗和煙云流體動力學仿真計算均得到了煙云流場從橢球形到蘑菇云形態的演變過程，仿真結果更清晰地顯示煙云流場由2 個反漩渦環流結構組成，實驗結果和仿真結果證明煙云擴散過程是一個高溫低密度浮力渦環運動的物理過程。

（2）實驗得到大氣穩定、無風、厚水泥地面、裸裝藥條件下煙云擴散高度H 隨時間t 變化的模型為：H(t)=(6.1±1)M(0.32±0.03)t(0.5±0.05)，在時間tmax=(28±1.1)M(0.33±0.04)時煙云趨于穩定，1、16、62 kg TNT 爆炸煙云的擴散高度分別在30、70、110 s 左右不再上升，最終煙云高度約為36、125、240 m。

（3）根據實驗結果認為Church 公式描述的煙云寬度是其高度的0.4 倍的結論不夠準確，討論了煙云寬度隨時間變化的擬合規律，結果顯示煙云寬度幾乎呈線性增大；發現煙云溫度隨時間快速單調遞減至常溫，煙云中溫度變化近似反比例函數規律。

（4）實驗初步討論了不同地面條件和不同殼體束縛下的煙云擴散高度。第2 組實驗顯示硬質地面條件會降低煙云上升高度(5～20)%，該條件下高度變化修正模型為H(t)= (6.3±1)M(0.29±0.03)t(0.5±0.05)，第3 組實驗則顯示厚殼體裝置煙云擴散高度略低于裸裝藥煙云擴散高度。

針對爆炸煙云擴散的研究目前較少，但對污染評估和爆炸偵測卻非常重要。下一步還將建立和修正不同爆炸裝置、不同地面高度、不同粒子攜帶、不同大氣環境下的煙云擴散模型，開發爆炸煙云擴散源項計算程序，以期為科學解釋和預測爆炸煙云這一物理現象提供參考。