基于支持向量機的建筑能耗預測研究

侯博文，譚澤漢，陳煥新*，孫劭波，龔麒鑒

（1-華中科技大學能源與動力工程學院，湖北武漢 430074；2-空調設備及系統運行節能國家重點實驗室，廣東珠海 517907）

0 引言

隨著人們對建筑室內環境與舒適度要求的逐步提高，在未來一段時間，我國公共建筑的能源消耗將呈現出進一步上升的趨勢[1]，雖然我國公共建筑能耗水平低于歐美發達國家，但是大型公共建筑的高能耗水平已經與歐美發達國家接近，因而對我國公共建筑進行能耗預測并試圖降低建筑能耗是一個重要的任務[2]。目前部分現有的商業建筑的錯誤控制策略可能造成設備故障，或者降低設備15%～ 30%的效率[3]。美國能源技術實驗室指出，只通過先進的建筑能源控制策略，便可降低美國2010年能源需求量的 1/4以上[4]。研究表明，建筑能耗是世界能源消耗總量很大的一部分，發達國家的建筑能耗占比達到總能耗的 30%～40%，例如，美國和歐洲的建筑能耗分別占能源消費量的 39%和40%[5]，而我國建筑能耗的占比也達到了 29%，這個比例也會隨著我國高層建筑數量的增加而提高。

近年來，基于數據驅動的建筑能耗預測研究越來越廣泛[6]。KADIR等[7]使用機器學習算法（包括支持向量機、人工神經網絡、決策樹和其他統計算法）的數據驅動型建筑能耗預測研究進行了回顧。ZHAO等[8]將建筑能耗預測方法分為復雜的工程方法、簡化的工程方法、統計方法、基于人工神經網絡的方法、基于SVM的方法和灰色模型；并從模型的復雜性、易用性、運行速度、所需投入和準確性等方面進行了比較分析。CHENG等[9]提出了一種基于數據驅動方法的通用的數據挖掘框架，闡述了在建筑空調系統內故障診斷的研究步驟。LI等[10]分別采用BP神經網絡、RBF神經網絡、GRNN神經網絡以及支持向量機對同一住宅的年總能耗量進行預測，結果表明，支持向量機預測模型相對于其他3個模型來說，預測精度最高。FUMO等[11]總結了各種研究提出的建筑能耗預測方法，并強調了對建模所用的模型校準和驗證以及對天氣數據的審查。

本文采用支持向量機算法建立能耗預測模型，并通過向量間的相關性分析，重要性排序選取最優特征向量，并采用交叉驗證、網格搜索等方法進行參數尋優來優化預測模型，采用平均絕對誤差（MAE）、平均根誤差（RMSE）和平均絕對百分比誤差（MAPE）作為模型評價的指標。

1 建筑數據來源

本文采用的建筑能耗數據來自河南省新鄉市某一政府辦公建筑，建筑總面積達25,000 m2。水源熱泵系統是冬季供暖的主要設施，可以給室內提供良好舒適的工作環境。水源熱泵系統主要由潛水泵、旋流除砂器、冷水機組、空調末端設備和循環泵 5個部分組成，供暖時的水源熱泵系統結構如圖1所示[12]。潛水泵一般安裝在水源內，用于提取淺層的地下水，旋流除砂器主要過濾地下水中的泥沙。冷水機組是水源熱泵系統中的重要一環，由蒸發器、壓縮機、冷凝器和膨脹閥4部分組成。冷卻水經冷凝器通過供水管道分配給建筑內的各個末端設備，整個過程由循環泵來提供動力。

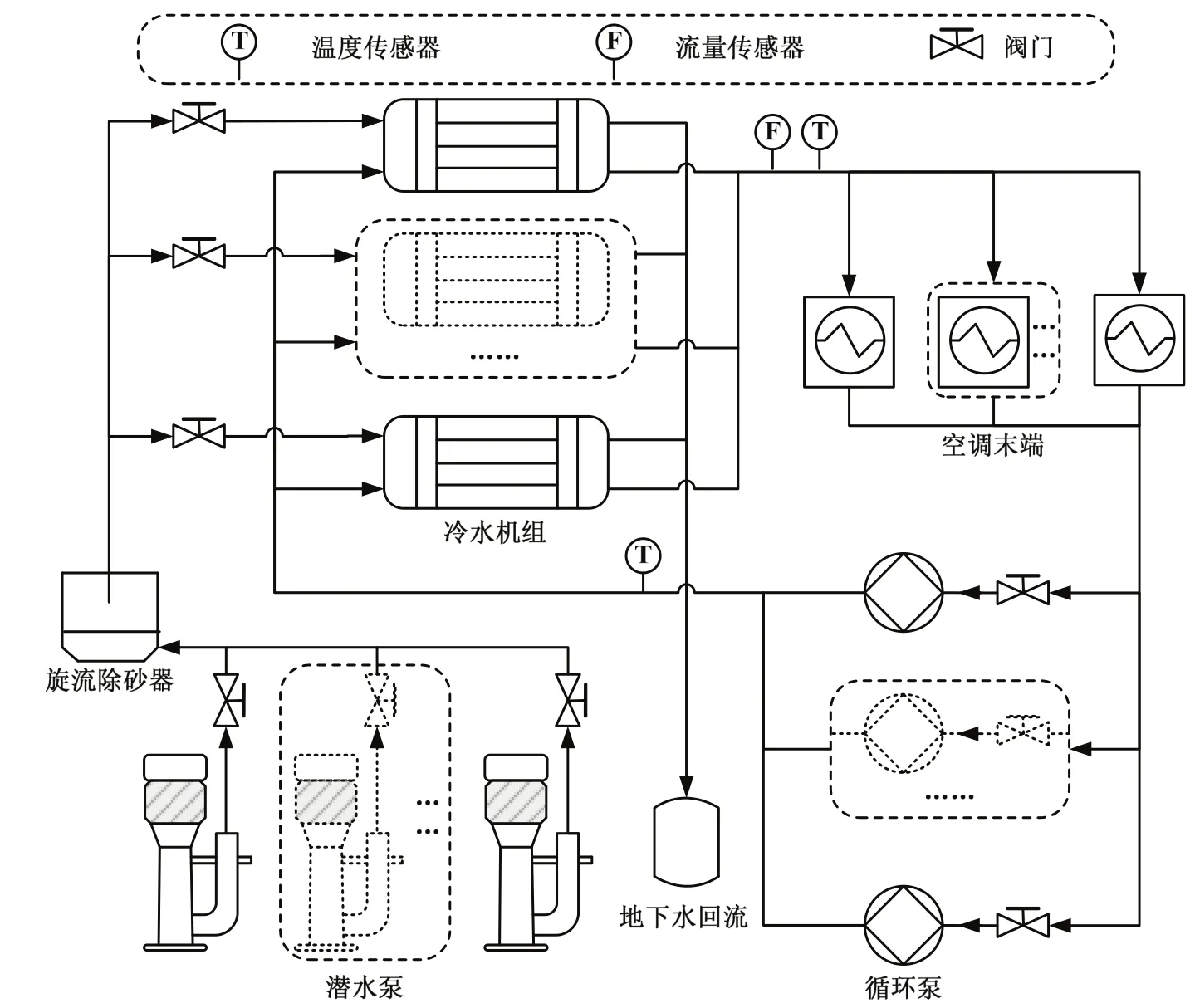
圖1 水源熱泵系統圖

數據采集系統是獲取數據的來源，本次課題在選取建筑物的水源熱泵系統上安裝了許多傳感器，這些傳感器匯集了關鍵參數數據，并將所有數據存儲在建筑物實時監測系統中，數據以5 min的間隔同時記錄。課題選用的數據為建筑物2016年11月23日至12月22日一整個月的供暖氣象數據，并對數據進行了異常值的檢測和剔除，選取其中的7個特征向量和輸出用電量作為本次分析數據，7個特征向量分別為天氣溫度、天氣濕度、室外風速、室外風向、光照強度、輻射強度和室外綜合溫度。數據特征如表1所示。

2 支持向量機原理與優化理論

2.1 支持向量機

支持向量機是一種基于內核的機器學習算法，可以用于回歸和分類，該算法即使在相對較少的訓練數據下也能很好地解決非線性問題。支持向量機對于解決非線性、高維度以及局部極小點等問題上有著突出的優勢，能在很大程度上提高模型預測的準確性，具有良好的應用價值。對于訓練樣本[13]：

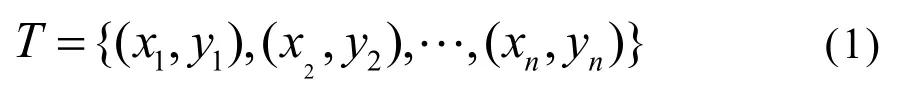
式中：

T——訓練樣本；

x——訓練樣本的輸入；

y——訓練樣本的輸出。

假設輸入x與y之間的函數關系為f(x)=WTx+b，其中W為權重系數向量，b為偏置項。擬合函數得到的回歸預測值與實際輸出值之間存在一定的誤差，當誤差較小時，這個誤差可以被接受。理想的狀態是，所有的訓練數據都能夠落在以ε為半徑的區域內，ε為允許誤差，當誤差小于ε時，誤差忽略不計；誤差超過ε時，超出的部分就要受到懲罰。對該問題進行優化，為保證優化問題有解，引入拉格朗日函數并求解，得到支持向量機的回歸函數為：

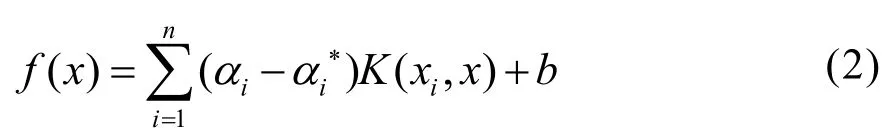
2.2 模型優化理論

2.2.1 相關性分析

Pearson相關系數、Speraman相關系數是最常用的兩種相關性系數的算法，本文目的是進行建筑的能耗預測，在此選用Pearson相關系數來說明變量之間的關系，具體公式如下所示：

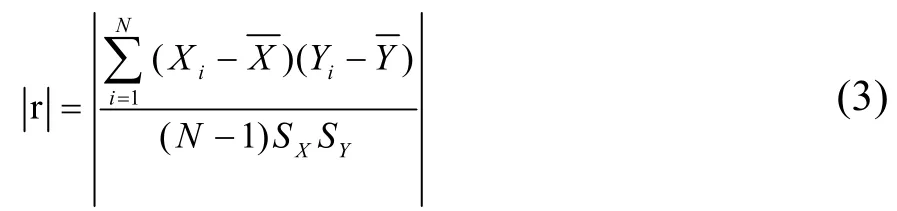
式中，r為兩個變量之間的相關性系數，N為數據中樣本的個數，Xi和Yi為兩個不同屬性列的第i個樣本值，SX和SY為X和Y列的標準差。

如果兩列間的相關性系數較大，就意味著兩個變量之間有著較大的線性關系，根據具體情況將其中的一個變量剔除。

2.2.2 重要性排序

通過特征選擇將高維空間的樣本用映射或者是變換的方式轉換到低維空間，達到降維的目的；然后通過特征選取刪除冗余和不相關的特征來進一步降維[14]，以獲得盡可能小的特征子集，不顯著降低預測精度，獲得較好的預測結果。

通過重要性分析進行特征選擇有兩個目標[15]：一是找到對輸出變量影響程度較大的變量，二是選出數目較少的特征變量并能較好地預測輸出變量。

2.2.3 參數尋優

非懲罰因子C和核函數參數g對基于支持向量機的能耗預測模型的預測結果有著很大的影響。本文采用交叉驗證和網格搜索的方法來進行參數尋優過程，以獲得最佳的模型參數。

交叉驗證是指在給定的建模樣本中，拿出大部分樣本進行模型的構建，留小部分樣本用剛建立的模型進行預測，能夠防止模型過擬合，本文采用十折交叉驗證的方法。

網格搜索法的基本原理[16]是讓C和g在一定的范圍內劃分網格并遍歷網格內所有點進行取值，在每一組C和g的取值下訓練模型，計算每組模型的均方根誤差，選取最終使得測試集預測效果最好的那組C和g的值作為最佳的參數。

2.3 模型評價指標

平均絕對誤差（MAE）、平均根誤差（RMSE）和平均絕對百分比誤差（MAPE）3個指標作為能耗預測模型的評價指標，具體公式如下所示：

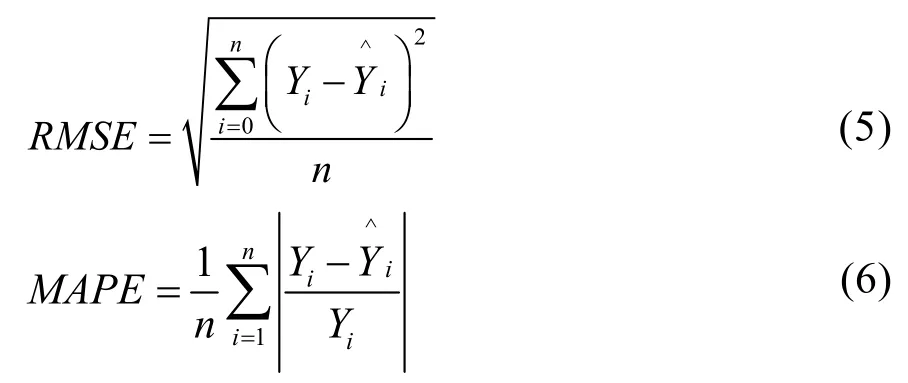
式中，n為樣本數據的個數，Yi為第i個樣本的實際值，為第i個樣本的預測值。

2.4 基于支持向量機的能耗預測模型

圖2為基于支持向量機的能耗預測模型的流程圖[17]，主要由3部分組成。

1）數據預處理：將原始數據中的異常值剔除，并對數據進行歸一化處理；

2）模型的建立：將剔除異常值后的數據按照3：1的比例分為訓練集和測試集，將訓練集中的數據輸入到支持向量機模型中；

3）模型的優化：通過相關性分析，重要性排序選取最優特征向量，并采用交叉驗證、網格搜索等方法進行參數尋優來優化預測模型。

3 結果分析

3.1 相關性分析

本文計算了兩兩變量之間的相關性系數，為了更好地展示效果，將其放入表格中進行分析，如表2所示。表中的數字大小代表著兩變量之間的相關性系數，數字越大就表示兩個變量之間的相關性越大。值得注意的是，對角線上的數字均為 1，這表明變量與自身之間的相關性系數為1。以表2中天氣溫度與第7列對應變量，即天氣溫度與室外綜合溫度之間的相關性系數為0.59，呈正相關；天氣濕度與第3列對應變量，即天氣濕度與室外風速之間的相關性系數為-0.41，稱負相關。

從表2中可以看出部分向量之間存在高度的線性相關，本文將相關性系數大于0.80的認為是高線性相關，并將其在表格中將數字加粗，由表2可以看出輻射強度與光照強度、輻射強度與室外綜合溫度、光照強度與室外綜合溫度之間存在較高的線性相關，在此將輻射強度與室外綜合溫度這兩個特征變量剔除掉，選取室外風速、天氣溫度、光照強度、室外風向、天氣濕度這5個變量作為模型的特征向量，此時變量之間就不存在兩兩之間相關性系數過高的結果。

3.2 重要性排序

圖3為能耗預測模型中向量的重要性排序，從圖3可以看出室外風速、天氣溫度、光照強度這3個特征向量對輸出向量的影響程度較大，3個變量加起來的相關性系數達到0.80，而室外風向和天氣濕度這兩個向量對輸出向量的影響程度較小。所有變量的重要度比例是按照總和為1來進行分配的。

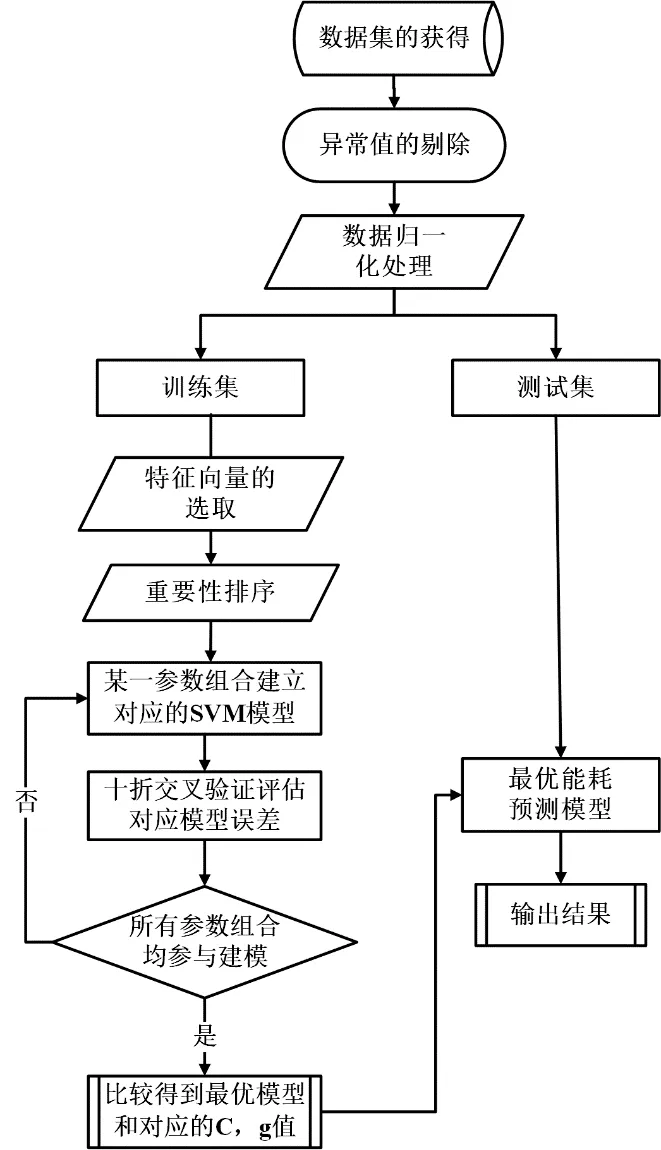
圖2 基于SVM的能耗預測模型流程圖

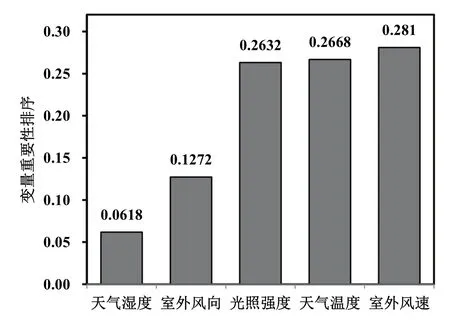
圖3 特征向量重要性排序圖

3.3 參數尋優

根據前期探索與嘗試，將懲罰因子C的范圍定為（2-2，29），核函數參數 g的范圍定為（2-5，26），使C和g都在2的指數范圍內進行交叉驗證，這樣一共產生144種C和g的組合。

在基于支持向量機的能耗預測模型[18]中進行網格搜索時，可能會得到多組的C和g的值都能使訓練的模型具有較高的預測精度，遇到這種選取參數的問題，原則是選取參數較小的一組。因為過大的C的取值會使模型在進行預測時出現過擬合的狀態，造成數據在訓練集內的預測精度很高，而在測試集中的數據進行測試時會出現預測精度很低的現象，即預測模型出現泛化性較低的現象。在參數尋優的實際過程中，為了使預測模型達到準確度最優的結果，往往選取成對的較小的C和g的值[19-20]。最終得到最優的參數是懲罰因子C為32，核函數參數g為0.5。

3.4 模型預測結果

得到優化后的能耗預測模型，命名為 SVR-B，得到預測值與實際值的散點圖如圖4所示。圖中實線代表預測值與實際值完全擬合，上下兩條虛線代表與實際值誤差為10%，即為實際值的90%和實際值的110%。同時計算SVR-B模型的誤差，平均絕對誤差MAE為3.97，均方根誤差RMSE為6.09，平均絕對百分比誤差MAPE為0.40。

將優化前后的模型預測結果進行對比，優化前的能耗預測模型命名為 SVR-A，SVR-A模型的預測結果如圖5所示。

通過圖4和圖5的對比，可以看出優化后的能耗模型預測結果精度更高。本文計算了 SVR-A模型和 SVR-B模型的誤差評價指標：平均絕對誤差（MAE）、平均根誤差（RMSE）和平均絕對百分比誤差（MAPE），如表 3所示，SVR-B模型的 3個指標相比于SVR-A模型的3個指標都有了大幅度的降低，模型的預測效果有較大程度的提升。MAE由之前的8.01降為最后的3.97，降低幅度為50.44%；RMSE由原來的12.61降為最后的6.09，降低幅度為51.70%；MAPE由原來的4.88%降為最終的0.40%，降低幅度為91.80%。

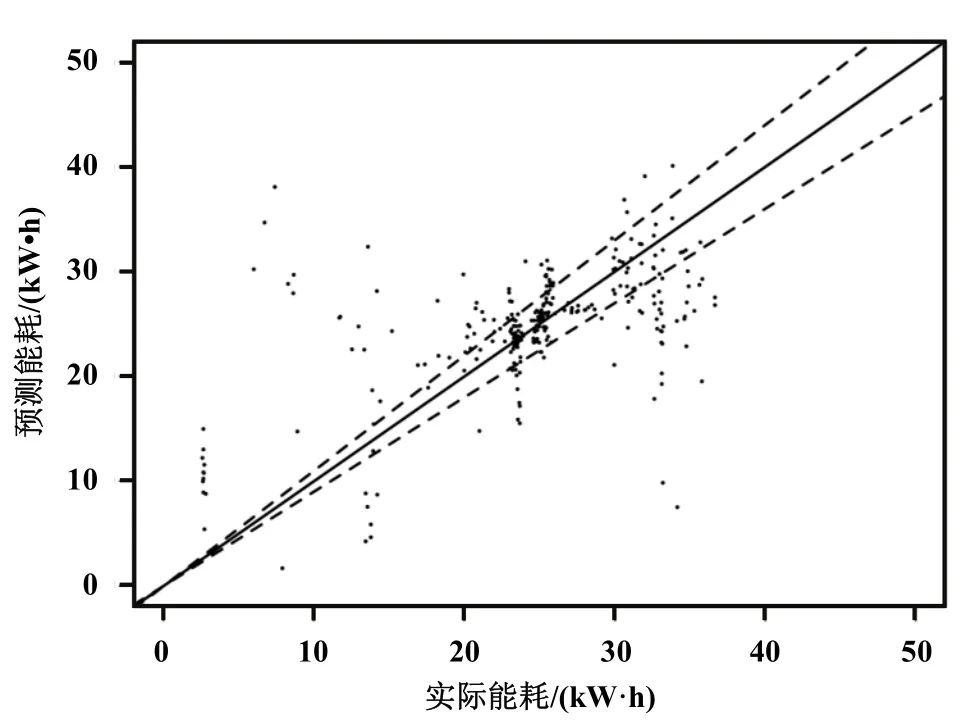
圖5 基于SVR-A模型的能耗預測結果

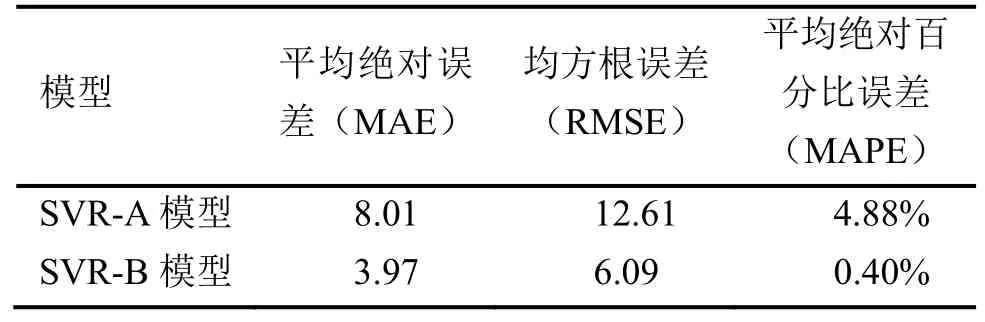
表3 模型評價指標對比表

4 結論

本文通過構建基于支持向量機的能耗預測模型來對建筑進行能耗預測，對比了實際測量值與模型預測值，并對能耗模型進行了優化，計算了相應的模型評價指標，得到結論如下：

1）經過優化后的支持向量機模型預測性能得到改善，平均絕對誤差由之前的 8.01降為最后的3.97，均方根誤差由原來的12.61降為最后的6.09，平均絕對百分比誤差由原來的 4.88%降為最終的0.40%；

2）本文將預測結果與測量值進行了對比，發現用電量低于15 kWh的數據預測能力不理想，分析原因認為未對開停機時的數據給予足夠重視。