基于多因子分析的無線傳感器網絡可靠性評估模型設計

芮立

摘 ?要： 采用判決反饋方法評估無線傳感器網絡時，僅從網絡鏈路穩定性因素方面考慮，未考慮影響網絡可靠性的多種因素，自適應能力和可靠性評估效果差。設計基于多因子分析的無線傳感器網絡可靠性評估模型，利用多因子分析過程將無線傳感器網絡復雜的變量關系簡單化。由5個主指標與20個有相互關聯的子指標建立無線傳感器網絡可靠性評估指標體系，通過主成分分析方法分析指標體系獲取11個無線傳感器網絡可靠性指標主因子。將這些因子輸入神經網絡模型中，構建無線傳感器神經網絡可靠性評估模型，完成無線傳感器網絡可靠性評估。實驗結果表明，該模型的可靠性評估精度均值為98%，該模型下的無線傳感網絡可靠性最高達到98%，極大提高了無線傳感器的安全性能。

關鍵詞： 多因子分析; 無線傳感器; 可靠性評估; 主成分分析方法; 神經網絡; 模型設計

中圖分類號： TN915?34; TP311 ? ? ? ? ? ? ? ? 文獻標識碼： A ? ? ? ? ? ? ? ? ? ?文章編號： 1004?373X（2019）12?0156?05

Abstract： Only the stability factor of the network link is considered， and various factors affecting network reliability are not considered when the decision feedback method is used for wireless sensor network evaluation， resulting in poor adaptive ability and reliability evaluation effect. Therefore， a reliability evaluation model based on multi?factor analysis is designed for the wireless sensor network. The complex variable relationship of the wireless sensor network is simplified by using the multi?factor analysis process. The reliability evaluation index system of the wireless sensor network is built by using five main indexes and 20 interrelated sub?indexes. 11 main factors for the reliability index of the wireless sensor network are obtained by analyzing the index system with the principal component analysis method. These factors are input into the neural network model to build the reliability evaluation model of the wireless sensor neural network， so as to complete the reliability evaluation of the wireless sensor network. The experimental results show that the mean value for reliability evaluation accuracy of the model is 98%， and the maximum reliability of the wireless sensor network under the model reaches 98%， which can greatly improve the safety performance of the wireless sensor.

Keywords： multifactor analysis; wireless sensor; reliability evaluation; principal component analysis method; neural network; model design

0 ?引 ?言

無線傳感網絡（Wireless Sensor Network，WSN）被大范圍應用在各個領域內[1]，WSN具備無線通信、成本低等優點。在確保WSN的可靠性的前提下，提高網絡智能服務效率，同時以解決網絡延遲、網絡冗余與環境干擾等性能指標問題為目標建立WSN，并且各個性能指標相互制衡[2]。建立的WSN是否符合實際要求是由建立各個性能指標和傳感器網絡可靠性之間的關系驗證。無線傳感網絡領域相關學者，越來越注重對網絡可靠性的研究，設計高質量的無線網絡可靠性評估模型具有重要的應用意義[3]。以往采用判決反饋方法評估無線傳感器網絡時，僅從網絡鏈路穩定性因素方面考慮，未考慮影響網絡可靠性的不同因素，自適應能力以及評估效果差。因此，本文從無線傳感網絡可靠性評估指標的多樣性出發，設計有效的無線傳感網絡可靠性評估模型，增強無線傳感器網絡可靠性[4]。

1 ?基于多因子分析的無線傳感器網絡可靠性評估模型設計

1.1 ?多因子分析

為了全面評估無線傳感器網絡的穩定性問題，在無線傳感器網絡內收集大量的，能體現網絡可靠性的多個變量，但無線傳感器網絡收集可靠性多變量大樣本的過程導致數據收集負擔加大。同時出現重復收集數據造成數據冗余問題，導致無線傳感器網絡的各個屬性不能依據各個變量響應，存在差異的變量并不代表輸電網的屬性差異，因為大量變量之間在大部分情形下具有一定的關聯性。反應無線傳感器網絡可靠性原變量中涵蓋的關鍵信息，通過在大量指標中選取少量的綜合性變量體現，將繁雜的變量關系簡單化的過程為多因子分析[5]。

大量的原變量信息被少量的相互獨立因子變量替代，這一替代過程為多因子分析需要考慮的方向，數學模型為：

采用因子分析將各初始變量劃分成：

1） 公共因子由整個變量內少量的因子形成;

2） 特殊因子由各變量自身存在的不同因素形成。

1.2 ?評估指標的多因子分析

由5個主指標與20個有相互關聯的子指標建立無線傳感器網絡可靠性評估指標體系[6]，同時各子指標與5個主指標相互關聯。多因子分析某地區無線傳感器網絡的20組穩定性評估指標的樣本數據。通過多因子分析了解到，指標樣本的巴特利球度檢驗幾率是0，檢測統計量是131.051。由此可得相關系數矩陣與單元陣差異明顯，并且依據KMO（Kaiser Meyer Olkin）的度量標準得知[7]，KMO<0.6時無法實施因子分析，本文KMO的值是0.826，能夠進行因子分析。

全部指標變量的共同方差數據由表1多因子分析的原始結果呈現。[B1?B20]為原始指標變量。采用因子分析方法獲取原始解下指標變量共同方差用第2列描述，其是從原有20個指標變量中獲取的20個特征值，那么可描述原指標變量的全部方差，指標變量的共同方差的平均值是1。第3列提取特征值時的共同方差是依據本文要求提取11個因子的條件提取，原始指標變量的數量比因子變量的數量多，所以各指標變量的共同度小于1。全部指標變量依據表1因子分析的原始結果得知共同方差均較高，不同指標變量信息被遺棄的幾率較低，則因子提取的整體效果較好[8]。

表1 ?多因子分析的原始結果

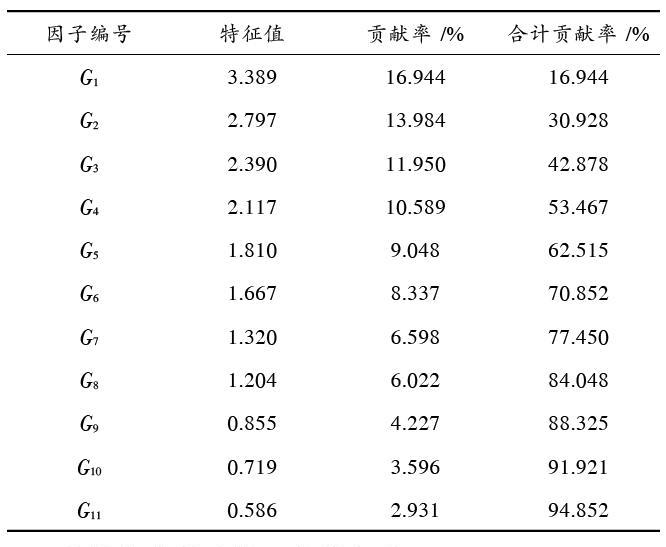
多因子分析貢獻率如表2所示。通過多因子分析可行性運算轉動后的因子載荷矩陣、貢獻率等信息結果。前11個合計貢獻率為94.852%，原20個指標變量大部分信息包括在提取的11個主因子內，因此可簡化提取11個無線傳感器網絡可靠性指標主因子。

表2內，因子編號為提取的11個主因子變量。公共因子[Gj]中的各變量[Xi]的因子負荷量的平方總計為特征值，其也是式（1）內[dij]的平方總計。各因子解釋原始數據的能力為因子貢獻率，通過各因子解釋的總方差度量，等同于各因子相關的因子負荷的平方和，該平方和為式（1）內[dij]的平方和。提取因子指標解釋原指標變量的能力為合計貢獻率，原始數據信息數量通過其體現。

評估指標之間的關聯性隨著指標變量的因子分析減少，無線傳感器網絡可靠性也可通過指標變量的因子分析結果，過濾低作用的指標變量，實現簡化計算[9]，提高無線傳感器網絡評估的準確性。通過表1可得原指標變量的94.852%信息由11個主因子指標獲取，同時降低了評估指標數量與評估成本，評估指標的科學性有所提升，為建立后續神經網絡可靠性評估模型確立可靠分析基礎。

表2 ?多因子分析貢獻率

1.3 ?無線傳感器網絡可靠性評估

1.3.1 ?神經網絡模型

隨著人工神經網絡（Artificial Neural Network，ANN）的不斷發展，ANN受到無線傳感器網絡分析人員的關注。大量的神經元（Neural）相互連接形成的網絡為ANN。ANN在信號處理機制中具有大范圍并行分布處理等屬性，相互連接的神經元間的連接權中反應了信息的存儲過程[10]。

ANN具備神經網絡運算能力、高度并行運算以及自適應性等優點，基于這些優點采用ANN可極大提高無線傳感器網絡可靠性運算自適應性和精度。

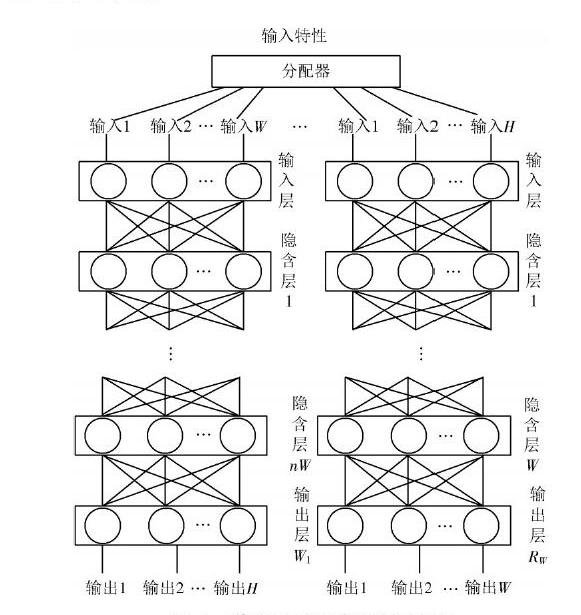
圖1描述神經網絡模型的結構，[W]為其輸入層的單元數，[K]為隱含層的單元數，[N]是輸出層的單元數。輸入模式由各個隱單元運算1個核函數，所有核函數線性加權和為分類器的輸出，則有：

訓練神經網絡模型內的各個子網滿足神經網絡的各個目的。一個多層神經網絡結構為一個子網。圖1內要求分配器將特定目標核函數分配給各子網，則依據不同子網的作用采用差異樣本進行訓練。之后子網輸出數據特征通過分配器檢索，獲取的檢索數據結果反饋給對應的子網。

圖1 ?神經網絡模型的結構

式中，期望輸出和真實輸出分別為[hrj]和[Qrj];網絡輸入向量的第[i]個元素為[irj]。

通過預處理器訓練樣本后，向神經網絡模型中輸入訓練樣本，可極大提高模型的訓練效率。變換輸入數據的域，即線性映射為預處理器。-1～1之間為輸入數據的值，0.1～0.9之間為輸出數據的值，訓練神經網絡時最靠近的域是輸出數據的值。為增強訓練算法的性能，將訓練樣本輸入與輸出數據的域通過處理器線性地轉換成上述的域。結束訓練后，最終輸出的數據由后處理器進行線性轉換到真實域中。

1.3.2 ?無線傳感器神經網絡可靠性評估模型

圖2為依據第1.2節的多因子分析結果獲取的11個無線傳感器網絡可靠性評估指標主因子，結合神經網絡模型構建無線傳感器網絡可靠性評估模型，采用該模型實現考慮影響無線傳感器網絡可靠性的多種因子情況下網絡可靠性的全面、準確評估。

2 ?實驗分析

實驗測試本文模型評估某無線傳感器網絡可靠性的有效性時，對比分析本文模型、馬爾可夫模型與云模型對無線傳感網絡評估的實驗網絡可靠性和傳感器密度的關系，結果如圖3所示。

圖2 ?可靠評估模型構建流程

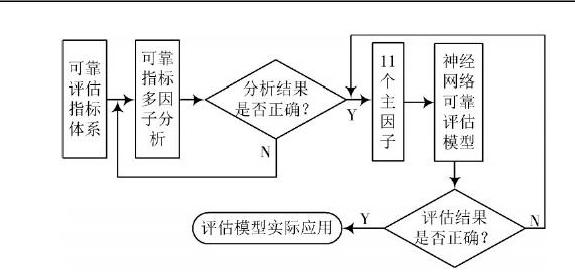
圖3 ?可靠性和傳感器密度關系

分析圖3可知，3種模型評估的無線傳感器網絡可靠性隨著傳感器密度增大而增大;本文模型評估的網絡可靠性平均值為49%，最高可靠性達到98%，馬爾可夫模型和云模型評估的網絡可靠性平均值為43.5%和25%，本文模型評估的無線傳感器網絡可靠性均值比其他兩種模型分別高5.5%和24%，說明本文模型評估下的無線網絡可靠性較高。

無線傳感網絡節點存活數目隨時間變化越穩定，時間越長，節點存活數目越高，說明無線傳感網絡越穩定，當無線傳感器網絡大小分別為100 m×100 m，200 m×200 m時，實驗檢測3種模型下無線傳感網絡節點存活數目與時間的對比情況如圖4所示。

實驗統計3種模型對上述兩種無線傳感器網絡進行可靠性評估的時間和精度情況，結果分別如表3與表4所示。

表3 ?3種模型可靠性評估時間

? ? ? ? ? ? ? ??

圖4 ?節點存活數目隨時間變化狀況

分析表3中3種模型對兩種無線傳感網絡實施可靠性評估的時間得知，無線傳感器網絡大小為100 m×100 m時，本文模型可靠性評估時間均值比馬爾可夫模型、云模型可靠性評估時間均值分別低6.72 s，7.5 s;無線傳感網絡大小為200 m×200 m時，本文模型可靠性評估時間均值比馬爾可夫模型、云模型可靠性評估時間均值分別低7.26 s，8.5 s，說明本文模型對無線傳感器網絡實時可靠性評估用時最短。

分析表4得知，無線傳感器網絡大小為100 m×100 m時，本文模型可靠性評估精度均值比馬爾可夫模型、云模型可靠性評估精度均值分別高12%，21%;無線傳感器網絡大小為200 m×200 m時，本文模型可靠性評估精度的平均值比馬爾可夫模型、云模型可靠性評估精度的平均值分別高13%，21%，說明本文模型更能精準完成無線傳感器網絡可靠性評估。

3 ?結 ?論

為了從多種角度充分考慮影響無線傳感網絡可靠性的因素，提高無線傳感器網絡可靠性評估的精度和全面性，本文設計基于多因子分析的無線傳感器可靠性評估模型。通過5個主指標與20個有相互關聯的子指標建立的無線傳感器網絡可靠性評估指標體系后，通過主成分分析方法獲取11個無線傳感器網絡可靠性指標主因子，達到過濾低作用指標變量，降低評估指標數量和評估成本，提高評估指標科學性的目的;將11個主因子作為神經網絡的輸入值，構建無線傳感器神經網絡可靠性評估模型，能準確評估無線傳感器網絡的可靠性。

參考文獻

[1] 劉邏，哈清華，王安邦.基于FABP的軟件可靠性增長模型[J].計算機仿真，2015，32（6）：440?446.

LIU Luo， HA Qinghua， WANG Anbang. Software reliability growth model based on FABP [J]. Computer simulation， 2015， 32（6）： 440?446.

[2] 劉創，王珺，杜蔚琪，等.基于網絡編碼的無線傳感器網絡多徑路由模型分析[J].計算機工程，2016，42（4）：37?43.

LIU Chuang， WANG Jun， DU Weiqi， et al. Analysis of multipath routing model in wireless sensor network based on network coding [J]. Computer engineering， 2016， 42（4）： 37?43.

[3] 趙治國，譚敏生，夏石瑩，等.基于時間因素的無線傳感網絡信任模型[J].計算機工程與設計，2017，38（4）：883?887.

ZHAO Zhiguo， TAN Minsheng， XIA Shiying， et al. Wireless sensor network trust model based on time factor [J]. Computer engineering and design， 2017， 38（4）： 883?887.

[4] 李建平，王曉凱.基于模糊神經網絡的無線傳感器網絡可靠性評估[J].計算機應用，2016，36（z2）：69?72.

LI Jianping， WANG Xiaokai. WSN reliability evaluation based on fuzzy neural network [J]. Journal of computer applications， 2016， 36（S2）： 69?72.

[5] 程紅霞，譚新蓮.多次重傳的鏈狀無線傳感網絡可靠性分析[J].計算機工程與應用，2018，54（5）：79?84.

CHENG Hongxia， TAN Xinlian. Analysis of reliability for wireless sensor network with chain topology based on multiple retransmission strategy [J]. Computer engineering and applications， 2018， 54（5）： 79?84.

[6] 王珺，杜蔚琪，劉輝，等.一種基于相交多徑網絡編碼模型的無線傳感網多徑路由協議[J].計算機科學，2016，43（11）：135?141.

WANG Jun， DU Weiqi， LIU Hui， et al. Multipath routing protocol based on braid?multipath network coding model for wireless sensor networks [J]. Computer science， 2016， 43（11）： 135?141.

[7] 王楓，祁彥鵬，傅正財.面向開關的復雜配電網可靠性評估簡化模型[J].電力系統及其自動化學報，2015，27（2）：57?63.

WANG Feng， QI Yanpeng， FU Zhengcai. Switch oriented simplified model of reliability evaluation of complex distribution system [J]. Proceedings of the CSU?EPSA， 2015， 27（2）： 57?63.

[8] 馬麗瑛，李劍波，王智穎，等.基于無線傳感器網絡的可靠性模型及上界[J].數學的實踐與認識，2016，46（12）：130?138.

MA Liying， LI Jianbo， WANG Zhiying， et al. The math model and the upper bound of the network reliability based on the wireless sensor network [J]. Mathematics in practice and theory， 2016， 46（12）： 130?138.

[9] 唐清明，趙菊敏，李燈熬，等.基于組合指標的無線傳感器網絡安全路由算法[J].電視技術，2016，40（11）：59?63.

TANG Qingming， ZHAO Jumin， LI Dengao， et al. Combination routing metric based routing algorithm for WSN [J]. Video engineering， 2016， 40（11）： 59?63.

[10] 楊棟，李書琴.自適應速率規劃的無線傳感器網絡傳輸優化模型[J].計算機工程與設計，2017，38（5）：1148?1151.

YANG Dong， LI Shuqin. Wireless sensor network transmission optimization model based on adaptive rate planning [J]. Computer engineering and design， 2017， 38（5）： 1148?1151.