一種新型補償策略下PFCBoost電路的環路穩定性研究

王曉凡 郭穎娜 程為彬 齊彥薇

摘 ?要： 針對傳統固定斜坡補償策略在AC?DC變換器中由于補償力度恒定造成輸入功率損失，功率因數降低等不足，介紹一種動態優化斜坡補償的方法，該補償策略在整個工頻周期內實時調整補償力度，實現了在一個開關周期內消除擾動誤差，有效提高了輸入功率和功率因數：同時對該補償策略下的AC?DC Boost 變換器進行小信號建模，分析了一個工頻周期內電流內環的零極點漂移現象，利用電壓外環對穩定性最差的過零時刻進行補償，保證了電路在整個周期內都滿足頻域穩定性要求，最后通過實驗驗證了該補償策略下電路的瞬態性能和頻域穩定性。

關鍵詞： 動態補償; AC?DC變換器; 環路穩定性; 輸入功率; 零極點漂移分析; 瞬態性能驗證

中圖分類號： TN721+.2?34 ? ? ? ? ? ? ? ? 文獻標識碼： A ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章編號： 1004?373X（2019）12?0076?05

Abstract： Since the traditional fixed slope compensation strategy used in the AC/DC converter has the deficiencies of input power loss and power factor reduction caused by constant compensation vigour， a dynamic optimized slope compensation method is introduced. The compensation strategy adjusts the compensation vigour within the whole power frequency period in real time， so as to eliminate the disturbance error within one switching period and effectively improve the input power and power factor. The small signal modeling is conducted for the AC?DC Boost converter under the compensation strategy. The zero?pole drift phenomenon of the current inner loop within one power frequency period is analyzed. The worst?stability at zero?crossing moment is compensated by using the voltage outer loop， so as to ensure that the circuit can meet the requirement of frequency domain stability within the whole period. The transient performance and frequency domain stability of the circuit under the compensation strategy were verified by an experiment.

Keywords： dynamic compensation; AC?DC converter; loop stability; input power; zero?pole drift analysis; transient performance verification

0 ?引 ?言

AC?DC Boost變換器采用的非線性元器件導致系統具有復雜的動力學特性[1]，所以有學者提出在峰值電流型AC?DC Boost中采取固定斜坡補償的策略來抑制這些不穩定行為，但是由于其補償力度恒定易造成電感電流過零死區，從而導致功率因數降低，輸入功率減小等問題。針對以上不足，本文介紹了一種動態優化斜坡補償的方法，在整個工頻周期內實時調整補償力度且使得補償電壓具有最強的鎮定能力，不僅在一個開關周期內消除擾動誤差，而且能夠消除固定斜坡補償中出現的零電流死區，有效提高功率因數，滿足了電路穩定的瞬態性能[2?3];并對動態斜坡補償下的PFC Boost 變換器進行小信號建模，分析了一個工頻周期內電流內環的零極點漂移現象，利用電壓外環對穩定性最差的過零時刻進行補償，保證了電路在整個周期內都滿足頻域穩定性要求，最后搭建實驗平臺驗證了電路運行的瞬態穩定性和頻域穩定性，證明了該補償策略增強了電路的抗干擾能力，對環路設計有著一定的指導意義。

1 ?動態斜坡補償分析

1.1 ?固定斜坡補償分析

斜坡補償策略的原理是在參考電流的基礎上加入一個微小的斜坡信號，消除快時標分岔等非線性行為，保證電路穩定運行。圖1是峰值電流型AC?DC Boost 電路結構圖。

圖1 ?峰值電流型 AC?DC Boost 電路結構圖

從圖1可以看出，控制環路由電流環和電壓外環組成，電壓外環為電流內環提供參考電流[i′ref]，其由PI控制器的反饋增益乘以一定的比例系數得到，這樣電感電流峰值跟蹤輸入電壓波形，通過電感電流的峰值與參考電流比較，產生對MOS管的控制信號。

當采取固定斜坡補償策略時，分析電路電感電流工作曲線如圖2所示。

圖2 ?固定斜坡補償電感電流工作波形

不難看出，固定斜坡補償使得電感電流平均值[iav]降低，輸入電流偏離了輸入電壓波形，在電流過零時刻產生死區，同時也在一定程度上降低了輸入功率。

1.2 ?全局動態優化補償分析

動態優化補償是采取參數共振的機理[4?6]，令特征值為0，此時補償電壓的斜率與電感電流下降斜率相等，系統具有最強的鎮定能力，電流的擾動誤差在一個開關周期內可以消除。動態斜坡補償時電感電流工作曲線如圖3所示。

圖3 ?動態斜坡補償電感電流工作波形

對比式（5）和式（2），可以看出動態斜坡補償的參考電流和電感電流平均值均被抬高，克服了固定斜坡補償輸入電流被降低的缺點，提高了功率因數;同時在每個開關周期補償電壓斜率實時調整等于電感電流下降的斜率，可以滿足一個開關周期內消除擾動誤差，提高了系統的穩定性。

2 ?小信號建模分析與環路設計

采取動態斜坡補償策略后，電路的瞬態穩定性得到保證，同時需要分析其頻域的穩定性[7?8]，對構成的等效功率級進行小信號建模得到其頻域模型。AC?DC Boost電路系統框圖如圖4所示。

圖4 ?AC?DC Boost電路系統框圖

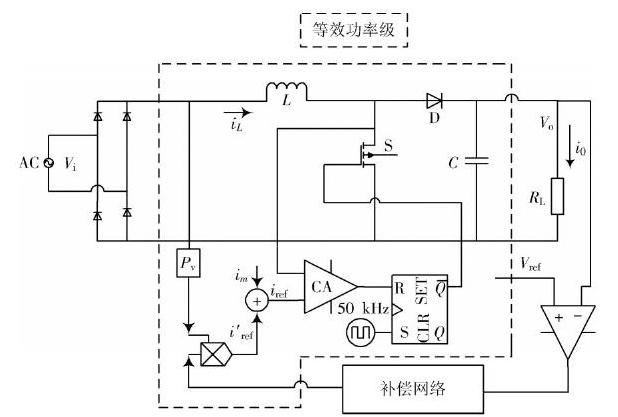
推導等效功率級的傳遞函數的思路是基于電感電流平均值的方程，考慮電感電流紋波和斜坡補償的影響[9?10]，得到占空比與其他控制量的表達式，然后與傳統的功率級傳遞函數相結合，從而得到精確模型。

對動態斜坡補償下的電感電流工作曲線線性化處理得到電感電流精確表達式：

表1 ?等效功率級傳遞函數相關具體參數

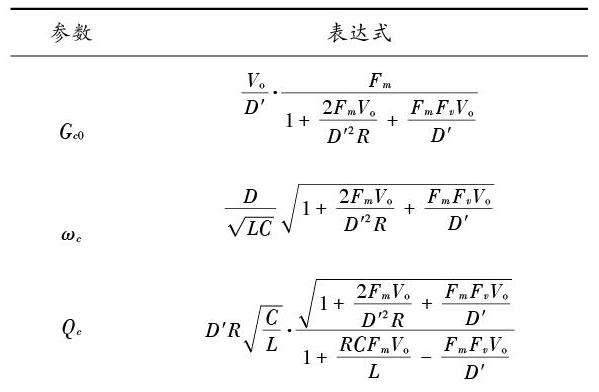
表2 ?電路設計參數

結合式（10）～式（13）將零極點表達式化簡成占空比的函數，并給出在整個工頻周期內零極點隨著占空比變化的圖像，如圖5所示。

圖5 ?零極點隨占空比變化曲線

從圖5可以看出來，在占空比變大時，即輸入電壓從峰值到零的過程中，高頻極點和右平面零點對應的頻率逐漸減小，且兩個頻率值之間的差值在縮小。所以在輸入電壓接近零時，由于右平面零點和高頻極點的頻率的減小和相互靠近造成系統的大幅度相位延遲，從而造成相位裕量過小，不能滿足頻域響應要求，容易產生不穩定的現象。因此必須對系統穩定性最差的情況進行補償，從而達到整個占空比變化的過程中都能滿足頻域響應的要求。針對電感電流過零，占空比最大時對電流內環進行補償，代入電路參數可以計算得到占空比最大時[fp1=1.5 Hz]，[fp2=8.5 kHz]，[fz=80 Hz]，直流增益[Gc0=11]。所以設計一個單極點的補償網絡以抵消右半平面零點為目的，單極點的補償網絡如下：

圖6 ?過零時刻幅相特性

經測量，[f=fc]時，相位裕量[?m=46°]，幅值增益等于1。在穩定性最差的情況下滿足頻域穩定性要求，從而保證占空比在整個工頻周期內變化頻域響應都穩定。

3 ?仿真與實驗驗證

3.1 ?仿真驗證

基于新的等效功率級的傳遞函數以及設計的電壓環，在Matlab軟件中搭建仿真電路，仿真結果如圖7所示。

圖7 ?電路仿真波形

從圖7可以看出動態補償消除了零電流死區，并且在每個開關周期補償電壓斜率與電感放電斜率保持一致，保證了一個開關周期內消除擾動誤差，同時電壓環補償后的電路在過零時刻保證電路穩定運行。

3.2 ?實驗驗證

在仿真電路的基礎上，依據前面提到的電路參數搭建了試驗電路并進行調試，得到實驗波形如圖8所示。

圖8 ?電路實驗波形

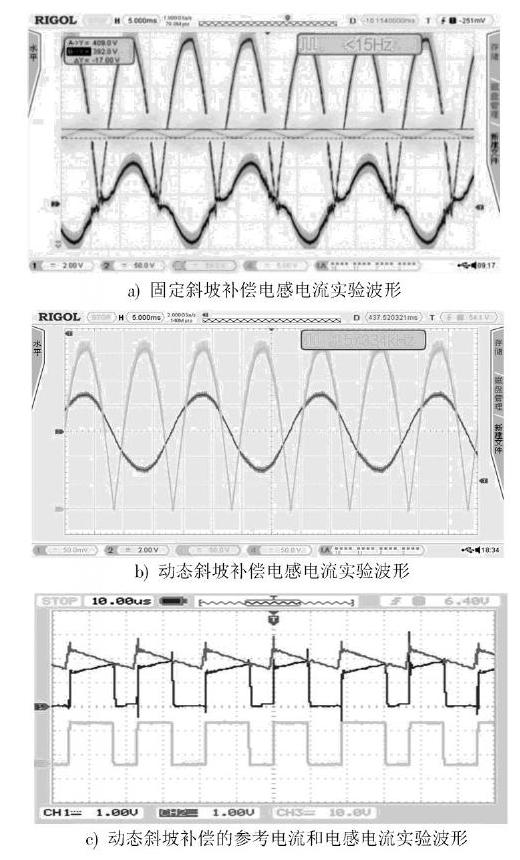
圖8表明，輸出電壓穩定在400 V，輸入電流完美跟蹤輸入電壓，消除了零電流死區，提高了功率因數，達到了電路設計要求;同時補償電壓在整個工頻周期內隨著輸入電壓實時調整，補償電壓斜率在每個頻閃周期都與電感電流下降斜率保持一致，保證了一個開關周期內消除誤差擾動，與仿真波形保持一致，實現了電路穩定運行，增強了電路的抗干擾能力。

4 ?結 ?語

本文對Boost電路的控制環路進行深入的分析，針對時域和頻域的不穩定現象采取了對應的補償策略進行補償，并搭建仿真電路和實驗電路進行驗證。結果表明，動態斜坡補償實時調整補償力度，抬高參考電流，消除了零電流死區，提高了功率因數;在頻域內經外環電壓環補償后的電路能夠穩定運行，具有較強的穩定性和抗干擾能力。所以，該補償策略同時滿足了時域和頻域的穩定性要求，具有良好的應用前景。

注：本文通訊作者為郭穎娜。

參考文獻

[1] 程為彬，金金，郭穎娜，等.峰值電流型PFC Boost變換器斜坡補償的時變模型和全局動態優化試驗[J].電子學報，2012，40（11）：2336?2341.

CHENG Weibin， JIN Jin， GUO Yingna， et al. Time?varying ramp compensation mode and global dynamic optimization experiment of peak current control PFC boost converter [J]. Acta electronica sinica， 2012， 40（11）： 2336?2341.

[2] CHENG W B， SONG J X， LI H， et al. Time?varying compensation for peak current?controlled PFC boost converter [J]. IEEE transactions on power electronics， 2015， 30（6）： 3431?3437.

[3] LU W G， LANG S， ZHOU L W. Improvement of stability and power factor in PCM controlled Boost PFC converter with hybrid dynamic compensation [J]. IEEE transactions on circuits and systems Ⅰ： regular papers， 2015， 62（1）： 320?328.

[4] 程為彬，康思民，汪躍龍，等.功率因數校正Boost變換器中快時標不穩定的形成與參數動態共振[J].物理學報，2011，60（2）：97?104.

CHENG Weibin， KANG Simin， WANG Yuelong， et al. Fast?scale instability and dynamic parameter resonance of power factor correction Boost converter [J]. Acta physica sinica， 2011， 60（2）： 97?104.

[5] 徐德鴻.電力電子系統建模及控制[M].北京：機械工業出版社，2005.

XU Dehong. Modeling and control of power electronics system [M]. Beijing： China Machine Press， 2005.

[6] 郭穎娜，程為彬，陳文奎，等.PFC Boost變換器次諧波振蕩抑制方法研究[J].現代電子技術，2016，39（16）：143?146.

GUO Yingna， CHENG Weibin， CHEN Wenkui， et al. Study on subharmonic oscillation suppression method for PFC Boost converter [J]. Modern electronics technique， 2016， 39（16）： 143?146.

[7] TSE C K. Flip bifurcation and chaos in three?state boost switching regulators [J]. IEEE transactions on circuits and systems Ⅰ： fundamental theory and applications， 1994， 41（1）： 16?23.

[8] YANG Yidi， LU Weiguo， IU H H C， et al. Stabilization of fast?scale instabilities in PCM boost PFC converter with dynamic slope compensation [C]// Proceedings of IEEE International Symposium on Circuits and Systems. Lisbon： IEEE， 2015： 2481?2484.

[9] PRAKASH K S， BARAI M. Time?variant slope compensation for peak current mode control （PCMC） of boost converter with point?of?load applications ?[C]// Proceedings of IEEE 6th International Conference on Power Systems. New Delhi： IEEE， 2016： 1?5.

[10] CHENG Weibin， GUO Yingna， TANG Nan. Parameter sine perturbation adjustment and stabilization of wide input boost circuits [J]. Acta physica sinica， 2012， 59（5）： 3035?3042.