鐵道車輛車下設備新型減振器設計研究

孫 煜， 宮 島， 周勁松， 孫文靜， 夏張輝

(同濟大學 鐵道與城市軌道交通研究院， 上海 201804)

采用動力分散的高速列車，牽引變流器、輔助變流器等設備直接吊掛在車體客室下，隨著列車運行速度的提高，采用輕量化設計技術的車體彈性振動加劇，車下設備直接吊掛于車體下方會對車體運行平穩性產生影響，如果吊掛方式不當，可能導致車體振動惡化，降低車輛運行平穩性。諸多學者對車下設備吊掛展開研究，周勁松等[1-2]將車體看作支撐在二系懸掛上的均質歐拉梁，采用動力吸振器原理，在車底安裝動力吸振器，可大幅降低車體振動。宮島等[3-4]提出將多個車下設備設計為車體各階彈性模態的動力吸振器，實現車體彈性振動的多模態控制，從而抑制車體彈性振動，提高車輛運行平穩性。張相寧等[5]針對高速動車組車下吊掛設備受力情況，研究了下吊設備懸掛自振頻率范圍，以隔振理論為基礎，提出采用橡膠減振器進行合理參數設計，以減小車下設備振動。于金朋等[6]利用典型車下設備與車體有限元模型，研究車下設備質量、隔振器剛度等對隔振性能的影響。然而，大多數關于車下設備吊掛的研究都是基于設備垂向吊掛剛度進行的，鮮見同時考慮設備垂向、橫向吊掛剛度的研究。其中主要原因是由于用于車下設備吊掛的橡膠元件存在固定的垂橫剛度比，一旦垂向剛度確定，橫向剛度即隨之確定，無法使垂向、橫向剛度同時實現最優值。針對這一問題，本文提出一種可以實現垂向、橫向吊掛剛度分離的車下設備新型減振器，克服了傳統橡膠元件固定垂橫剛度比的缺點，為車下設備吊掛元件設計提出新思路。

1 基于負剛度的新型減振器設計原理

橡膠彈簧對沖擊和高頻振動有良好的吸收效果，能承受多向載荷，常用作車下設備彈性吊掛減振元件。橡膠彈簧可以分為壓縮型、剪切型和復合型，軌道車輛車下設備彈性吊掛通常用壓縮型橡膠彈簧，其垂向剛度kz和橫向剛度ky之比(垂橫剛度比)通常在4.5以上[7]，即kz≥4.5ky，為了研究方便，本文采取垂橫剛度比為4.5的圓柱形橡膠彈簧作為車下設備彈性吊掛原件，其三向剛度關系為：kz=4.5ky，ky=kx。

以往的車下設備彈性吊掛設計中，通常僅考慮垂向減振，當橡膠彈簧以垂向剛度為目標設計之后，其橫向、縱向剛度則已確定。而實際上，僅考慮垂向吊掛剛度時，雖然垂向振動得到了有效控制，但橫向振動控制卻無法取得最優效果。因此，同時考慮車下設備的垂向吊掛剛度和橫向吊掛剛度顯得很有必要。

圖1 碟形彈簧特性曲線

利用碟形彈簧的負剛度特性，將其與橡膠彈簧并聯，設計車下設備新型減振器。具體步驟如下：首先，設計橡膠彈簧，使其橫向剛度與橫向剛度目標值相等；然后，設計碟形彈簧，使其在平衡位置的負剛度與橡膠彈簧垂向剛度疊加后同垂向剛度目標值相等；最后，設計滾動機構，釋放碟形彈簧橫向、縱向自由度，使其提供的橫向、縱向剛度為零。其設計原理示意圖如圖2所示。

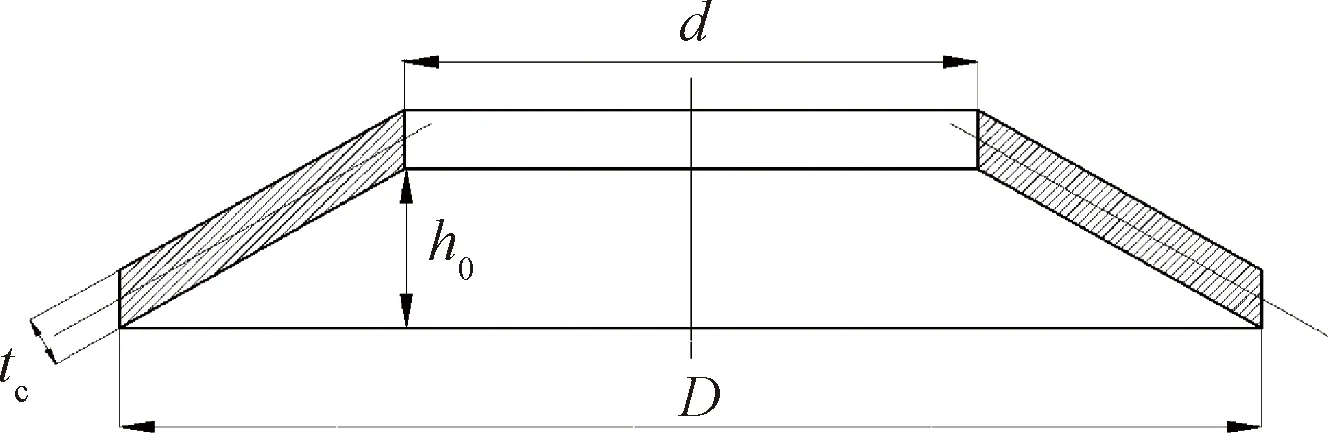
圖3 碟形彈簧截面示意

無支撐面碟形彈簧截面示意圖如圖3所示。圖中，tc為厚度；D為外徑；d為內徑。通常，無支撐面碟形彈簧(外內徑之比C=1～4)受力可表示為[7]

( 1 )

式中：E為彈性模量；μ為泊松比；x為碟形彈簧從初始位置沿垂向產生的位移；K1與外內徑之比C(C=D/d)有關，為

( 2 )

( 3 )

式( 3 )對x進行求導，可得碟形彈簧剛度表達式為

( 4 )

( 5 )

新型減振器剛度-位移曲線如圖4所示，其中kai為剛度設計目標值；kdx為通過式( 4 )計算得到的碟形彈簧剛度曲線；kxj為所并聯的橡膠彈簧剛度；kxj=kz+kdx即為最終獲得的新型減振器垂向剛度曲線。從圖4中可以看出，當系統在平衡位置附近振動時，新型減振器垂向剛度ka可達到剛度設計目標值kai。

圖4 垂向剛度-位移曲線

2 新型減振器垂向傳遞率分析

新型減振器在垂向力作用下，其回復力F包括正剛度橡膠彈簧回復力和負剛度碟形彈簧的回復力，可以表示為

( 6 )

為求解強迫振動下的解，對式( 6 )進行坐標變換，并無量綱化，令

( 7 )

可得無量綱表達式為

( 8 )

(1+β)αkxjtc=mg

( 9 )

對系統施加強迫振動激勵力fe=Fecos(ωt+θ)，其中，Fe為激勵幅值；ω為激勵頻率；θ為相位，可得其運動微分方程為

(10)

為方便求解，將式(10)轉換為無量綱形式，令

(11)

式中：ωn為傳統線性系統固有頻率；Ω為激勵頻率與傳統線性系統固有頻率之比，聯立式( 6 )～式(11)整理可得

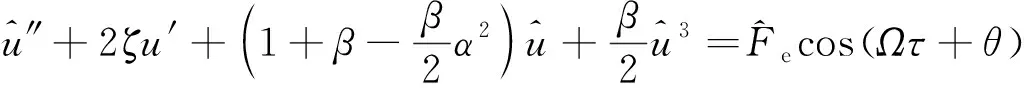
(12)

(13)

此方程為受強迫振動的Duffing方程[8]，令其解為

(14)

式中：A為位移響應幅值，將式(14)代入式(13)整理可得

(15)

采用諧波平衡法，令上式中各諧波系數相等，并忽略高階諧波，可得

(16)

將式(16)兩式左右兩邊平方相加，可得

(17)

通過求解式(17)，可以得到系統在強迫振動下的解。系統通過減振器后的無量綱力可表示為

(18)

(19)

由此可得系統傳遞函數為

(20)

基于式(17)和式(20)，新型減振器垂向振動力傳遞函數如圖5所示，其中，虛線部分是不穩定解。從圖5中可以看出，新型減振器傳遞函數共振頻率隨著激勵幅值的增大而增大，且共振幅值也隨著激勵幅值的增大而增大。

圖5 垂向傳遞率

3 仿真模型的建立

隨著對高速列車車輛系統研究的不斷深入，單純將車體看作剛性體無法反映出車體的彈性振動。為此，在動力學研究中需要將車體的局部柔性振動考慮在內，與原來單純的剛性系統相比，柔性系統考慮了柔性體自身變形與整個系統的耦合振動[9-10]，使虛擬樣機仿真試驗更接近于真實情況。本文采用SIMPACK多體動力學仿真軟件，建立考慮車下設備的高速動車組剛柔耦合動力學模型，進行仿真計算。

為得到包含車體彈性的剛柔耦合動力學模型，需要建立車體有限元模型，運用縮聚理論[11]對車體有限元模型進行縮聚計算，生成包含車體結構及模態信息的模型文件，通過SIMPACK軟件的FEMBS接口導入動力學模型。

建立完整單車車輛系統剛柔耦合動力學模型，包括1個彈性車體、2個轉向架、8個軸箱、4個輪對、1個車下設備，與車體相比，轉向架、軸箱及輪對由于彈性變形相對較小，仍考慮為剛性。其中，根據車體彈性對振動能量的貢獻[12]，車體彈性僅考慮主要低階彈性模態，其中一階垂向彎曲頻率為10.11 Hz，一階橫向彎曲頻率為13.27 Hz。在模型中還考慮二系橫向彈性止檔的遞增剛度特性、輪軌接觸非線性幾何特性、非線性蠕滑力和蠕滑力矩、液壓減振器的非線性特性。所建立的精細化高速動車組剛柔耦合動力學單車模型如圖6所示。

圖6 剛柔耦合系統動力學模型

為得到車下設備吊掛的最佳垂向及橫向吊掛剛度值，分別選取不同組合的垂向、橫向剛度進行優化計算。采用圓柱型橡膠，其特點是橫向剛度與縱向剛度相等。計算過程中，將車下設備垂向吊掛頻率fz、橫向吊掛頻率fy作為變量，則車下設備垂向、橫向、縱向吊掛剛度kz、ky、kx分別為

(21)

式中：me為車下吊掛設備質量；n為吊掛點數量。各種橡膠件的阻尼比不同，阻尼比太大，橡膠容易發熱，加速老化蠕變的過程。通常天然橡膠的阻尼比為0.005～0.075[13]，本研究阻尼比選取為0.06。

4 車下設備吊掛剛度最優值計算分析

根據車下設備質量及垂向吊掛剛度，可得設備吊掛頻率fz與靜撓度δst分別為[14]

(22)

從式(22)可以看出，吊掛頻率直接決定了吊掛剛度及靜撓度，如果吊掛頻率過低，會導致設備靜撓度太大，產生設備超過限界等問題。因此，本研究選取設備吊掛垂向、橫向計算頻率范圍均為4～16 Hz，步長為1 Hz。

圖7 設備吊掛頻率對車輛運行平穩性Sperling指標的影響

仿真過程中，車輛速度為350 km/h，軌道不平順采用低激勵高速譜[15]，計算車體前轉向架、后轉向架及車體中部的垂向、橫向車輛運行平穩性Sperling指標，計算結果如圖7所示。圖7(a)是設備吊掛頻率對橫向平穩性(前、后轉向架及車體中部橫向平穩性Sperling指標的算術平均值)的影響，從圖中可以看出，當設備吊掛頻率為垂向7 Hz、橫向13 Hz時，車輛運行平穩性最佳；圖7(b)是設備吊掛頻率對垂向平穩性的影響，從圖中可以看出，當設備吊掛頻率為垂向9 Hz、橫向12 Hz時，車輛運行平穩性最佳；圖7(c)是設備吊掛頻率對垂向和橫向Sperling平均值的影響，從圖中可以看出，當設備吊掛頻率為垂向9 Hz、橫向12 Hz時，運行平穩性最佳。綜合圖7(a)～7(c)可得，相對于橫向吊掛頻率，運行平穩性對垂向吊掛頻率更加敏感；當設備吊掛頻率取垂向9 Hz、橫向12 Hz時，車體振動最小，車輛運行平穩性最佳，這是由于此時車下設備相當于動力吸振設備，降低了車體的彈性振動。本研究中設備與車體質量比κ=0.2，基于加速度響應的動力吸振原理，滿足最優同調條件的頻率比γ為[16]

(23)

根據車體一階垂向彎曲頻率10.11 Hz和一階橫向彎曲頻率13.27 Hz，可以計算出車下設備垂向與橫向最優吊掛頻率理論值分別為9.23、12.12 Hz，而仿真計算所得設備最優吊掛頻率值與其接近。

5 新型減振器參數設計

通過上一節分析可知，設備吊掛頻率最優值為垂向9 Hz、橫向12 Hz，本研究中設備質量為6 400 kg，吊掛點數為4，根據式(21)可得設備每吊掛點目標剛度值為垂向5.12×106N/m、橫向9.10×106N/m。依據橡膠彈簧垂橫比，可得新型減振器中橡膠彈簧垂向剛度為4.09×107N/m。那么，新型減振器中碟形彈簧在平衡位置的負剛度即為-3.58×107N/m。由此可以設計碟型彈簧參數，見表1。

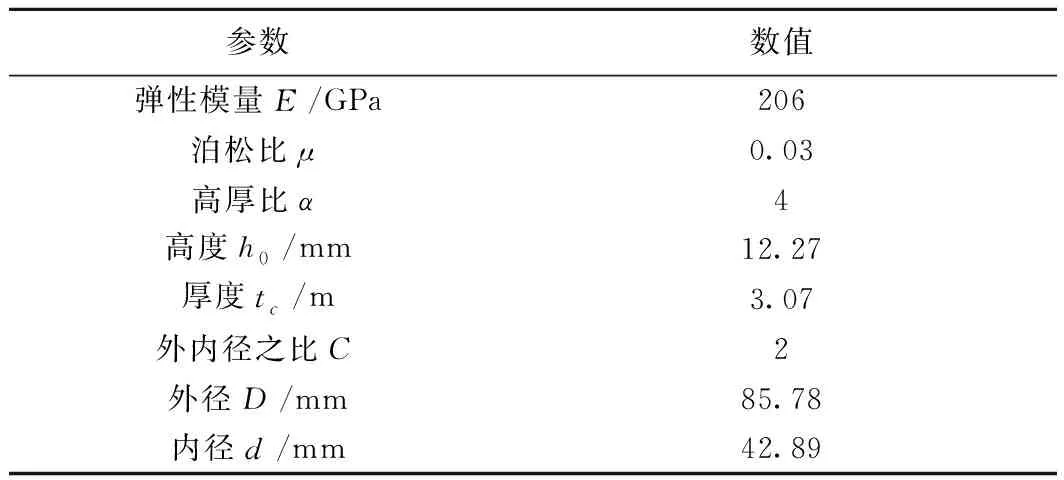
表1 碟形彈簧各參數

6 仿真結果對比分析

為了研究新型減振器的減振效果，將車下設備采用新型減振器的車輛與車下設備采用傳統橡膠減振元件的車輛進行仿真對比。計算時，傳統橡膠減振元件以垂向剛度值為目標值設計，其橫向剛度根據垂橫剛度比計算得到，則傳統橡膠減振元件的垂向剛度和橫向剛度分別為5.12×106、1.14×106N/m。

表2為車下設備采用新型減振器的車輛與采用傳統橡膠減振元件的車輛運行平穩性Sperling指標計算結果對比，其中平均值是前轉向架、車體中部、后轉向架的Sperling指標算術平均值。從表2中可以看出，車下設備采用新型減振器的垂向和橫向運行平穩性明顯好于傳統橡膠減振元件。

圖8(a)與圖8(b)分別為車體中部地板面橫向、垂向振動加速度功率譜密度對比結果。圖8中可以看出，新型減振器得到的車體中部地板面橫向振動加速度功率譜密度在9～16 Hz及垂向振動加速度功率譜密度在9～12 Hz明顯優于傳統橡膠減振元件，說明新型減振器能夠有效降低車體彈性振動，提高車輛運行平穩性。

表2 兩種減振器對車輛運行平穩性Sperling指標的影響

圖8 車體振動加速度功率譜密度

7 結束語

本文提出一種可以實現垂向、橫向吊掛剛度分離設計的車下設備新型減振器。建立包含車體彈性的高速動車組剛柔耦合動力學模型，以車輛運行平穩性最優為目標，計算獲得車下設備垂向與橫向最優吊掛頻率分別為9、12 Hz，并據此設計車下設備新型減振器參數。對比分析車下設備采用新型減振器的車輛與車下設備采用傳統橡膠減振元件的車輛運行平穩性及車體振動加速度功率譜密度，結果表明，相對于傳統橡膠減振元件而言，采用新型減振器的車下設備可以有效降低車體的彈性振動，同時改善車輛的垂向與橫向運行平穩性。