改進的最優小波基選取方法與跳頻信號檢測研究

鄭 洋，陳西豪，朱 銳

（空軍工程大學信息與導航學院，西安 710077）

0 引言

隨著計算機技術向軍事領域的不斷滲透，電磁環境的復雜度也在日益增大，進而給通信對抗帶來極大的挑戰[1]。在這種條件下，抗干擾性強、組網能力強的跳頻通信必然會在軍事通信與通信對抗中發揮重要作用。為了在通信對抗中占據優勢，開展對非合作條件下跳頻信號檢測技術的研究，具有重大的理論意義與實際價值[2]。

時頻分析[3]是檢測跳頻信號的主要方法，對于獲取跳頻信號的信息具有極大的幫助。但是，窗函數的存在使得時間分辨率和頻率分辨率難以有效兼顧。針對這個問題，文獻[4]提出了一種基于小波分解與希爾伯特-黃變換的方法，極大地提高了檢測效果。小波分解與重構對接收到的跳頻信號進行去噪處理，但是為了取得最佳的去噪效果，需要對最佳小波基以及最佳分解層數進行研究確定。文獻[5]通過分解重構過程中信噪比的變化情況來確定最優分解層數。隨著分解層數的增加，噪聲在重構信號的比重先下降后上升，因此，信噪比呈現出先增大后減小的趨勢，利用信噪比的這種變化情況，有效地確定了最佳的小波分解層數。

對于最優小波基的選取，文獻[6]將幾種常用的小波去噪評價指標進行融合。首先按照需求篩選合適的指標，然后作歸一化處理并進行組合。這種融合的方法在信號真值已知的條件下，對小波去噪質量評價和最優小波基的選取有十分有效的指導作用。但對于非合作通信條件下接收到的跳頻信號而言，信號真值是未知的，接收到的是信號與噪聲的混合信號，因此，這些以信號真值已知為條件的評價指標和指標融合的方法就失去了應用條件[7]。

評價小波去噪質量還有一種方法是信噪比與信噪比增益的方法[8]。這種方法不需要原始信號的信息，在信噪比未知的情況下也同樣適用，但在非合作通信條件下，信號真值未知，該方法失去了應用的條件。本文改進了這種方法，在每次分解重構后對重構信號的信噪比進行盲估計，通過對比幾種常用的小波基的結果，分析并選擇最優小波基。仿真實驗證明，該方法極大地提高了非合作通信條件下跳頻信號去噪小波基選取的準確性。

1 信號模型

本文的跳頻信號模型為：

式中，s（t）是跳頻信號，n（t）是均值為 0，方差為 σ2的高斯白噪聲，跳頻信號和高斯白噪聲相互獨立，其中

式中，t為觀測時間；T0為跳頻信號起跳時間；Th為跳頻周期；fk是第k個時隙的跳頻頻率。rectTh表示時間寬度為Th的矩形窗函數，其表達式為：

基于小波分解與希爾伯特-黃變換的跳頻信號檢測方法的思想為：首先用小波分解對接收到的跳頻信號去噪處理，然后通過希爾伯特-黃變換實現檢測。為了達到最佳的去噪效果，在用小波去噪時需要重點解決兩個問題：最佳分解層數確定和最優小波基選取。對于最佳分解層數的確定，文獻[9]中已經作了一定的研究并得出了指導性的結論。本文就最優小波基的選取進行深入研究。

2 最優小波基選取

用小波變換對跳頻信號進行去噪，其實是利用小波的多分辨率特性對跳頻信號進行分解，即通過小波變換將原信號分解為原信號頻段內不同頻率的信號。分解后，有用的信號留在低頻部分，而高頻部分多屬于噪聲。然后利用這個特點對高頻信號部分進行處理，達到去除噪聲的目的。最后重構剩余信號，得到去噪后的信號[10]。

2.1 傳統評價指標

在利用小波變換去噪時，選擇不同的小波基，就會得到不同的變換結果。對跳頻信號，如何確定最優小波基來保證最佳的去噪效果，這就需要一個評價準則來指導選擇最佳小波基。當前，評價小波去噪質量的指標有：均方根誤差、平滑度、互相關系數和信噪比與信噪比增益。

2.1.1 均方根誤差（RMSE）

均方根誤差指經過分解并重構之后的去噪跳頻信號與原始跳頻信號的均方誤差，即：

2.1.2 平滑度

平滑度是指在信號足夠長時，去噪信號一階差分的方差根與原始信號一階差分的方差根之比，記為r，表達式為：

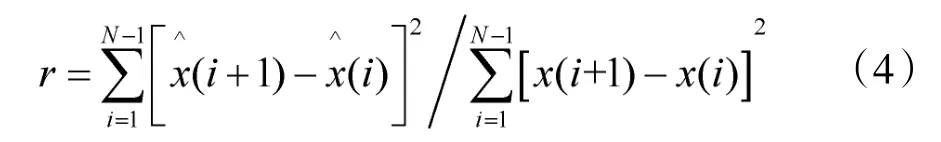
平滑度反映了去噪信號的平滑程度，信號越光滑，平滑度的值就越小，去噪效果越好。

2.1.3 互相關系數

互相關系數指去噪信號和原始信號兩種信號之間的相似度，記為R，表達式為：

R值越大，則去噪效果越好。

2.1.4 信噪比和信噪比增益

信噪比是指原始信號能量與噪聲能量的比值，記為SNR，其表達式為：

其中，ps是信號功率，pv是噪聲功率。信噪比增益是指去噪后的信號信噪比與原始信號信噪比之比，記為GSNR，其表達式為：

其中，SNRdn是去噪后的信號的信噪比，SNRn是原始信號的信噪比。實際情況下，SNR和GSNR的值越大，去噪效果越好。

2.2 多指標融合的小波去噪質量評價方法

每個評價指標描述的是小波去噪不同方面的性能，單一的評價指標無法對小波基的選取做出合理指導。為了最大限度地滿足小波去噪質量評價需求，進而有效地選取最佳小波基，在信號真值已知的情況下，文獻[11]將這些評價指標進行篩選并優化組合。其思想是：首先選取從不同角度衡量去噪效果的指標，保證評價體系的全面性；同時考慮所選指標的值與評價效果的相關性，以正相關為宜。然后歸一化處理并進行簡單組合。具體做法如下：

PRMSE、Pr分別為歸一化后的均方根誤差和平滑度參數。設通過組合得到的新的評價指標為H，則

H值越小，小波去噪效果越好。

2.3 改進的最優小波基選取方法

當信號真值已知時，上述方法對于評價小波去噪效果有重要的指導意義，但在非合作通信條件下，接收到的跳頻信號是帶有噪聲的混合信號，原始信號是未知的，此時上述方法失去了使用的先決條件。故本文改進了信噪比與信噪比增益的方法。利用信噪比盲估計來分析分解重構過程中信噪比和信噪比增益的變化情況，進而分析小波對跳頻信號的去噪效果，并確定最佳分解層數。此時，信噪比與信噪比增益的表達式分別為：

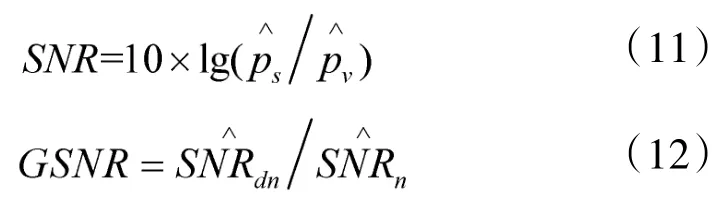
3 基于協方差矩陣分解的信噪比估計

對接收信號采樣得：

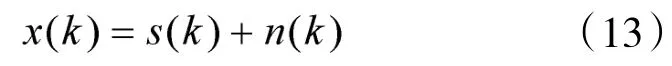
其中，k為抽樣時間點。

由于跳頻信號和噪聲是獨立分布的，且噪聲為高斯白噪聲，因此，采樣信號的協方差矩陣即為其自相關矩陣：

式中，H表示共軛轉置；自相關矩陣Rxx為m階方陣。

由于相關矩陣Rxx、Rss以及Rnn都是對稱矩陣，故可以進行奇異值分解（SVD）：

其中，

V是正交矩陣。則：

式中，由m個對角線元素張成的空間被稱為含噪信號空間，由前p個元素張成的空間被稱為信號子空間，后m-p個元素張成的空間被稱為噪聲子空間。則信號功率和噪聲功率可表示為：

則接收信號的信噪比為：

由于上式中的噪聲功率包含了信號帶以外的噪聲功率，而在實際情況下，對接收信號濾波處理后，只含有帶內噪聲，此時信噪比應調整為：

然后需要對信號空間維數p進行估計，文獻[12]提出了一種最小描述長度準則（MDL）：

其中，

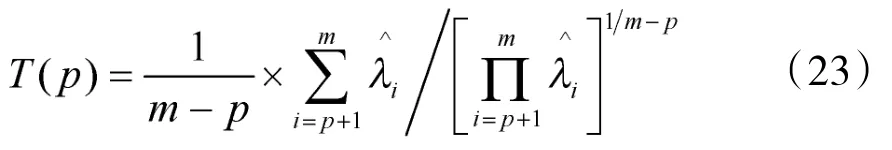
則信號空間的維數p表示為：

將其帶入式（21），得到信噪比估計值。

在用協方差矩陣估計信噪比的過程中，需要構造自相關矩陣、計算奇異值等，具體過程如下：

N為信號序列長度，m為相關序列長度，它的取值會對自相關矩陣的估計產生影響，實驗證明，m一般取40～100比較合適。

5）計算信噪比。

4 基于W-H的跳頻信號檢測算法

現有的跳頻信號檢測方法在去抗噪性以及時頻聚集性方面有待改進，據此提出了基于W-H的跳頻信號檢測算法。該方法結合了小波去噪與希爾伯特-黃變換的優點，算法流程如下：

1）利用小波分解去除混合信號中的噪聲；

2）將剩余信號進行小波重構，得到去噪后的信號；

3）利用希爾伯特-黃變換處理去噪后的信號，實現跳頻信號檢測。

5 最優小波基選擇流程

1）對接收到的跳頻信號進行信噪比估計，計算接收信號的信噪比；

2）對接收的跳頻信號進行1層小波分解，并進行重構，然后計算重構信號的信噪比，并計算信噪比增益；

3）繼續2層小波分解并重構，計算重構信號的信噪比，并計算信噪比增益；

4）對跳頻信號進行3層小波分解并重構，計算重構信號的信噪比，并計算信噪比增益；

5）比較得到的信噪比和信噪比增益，分析篩選最優小波基。

為了實驗的可靠性和準確性，本文還設立了一組對比試驗，在同等條件下原始信號已知的情況下，利用多指標融合的小波去噪質量評價方法進行仿真試驗并與本文方法的結果進行對比。

6 仿真實驗分析

分別按照兩種方法進行仿真試驗，結果如下：

表1 小波基‘coif4’的實驗結果

表2 小波基‘sym6’的實驗結果

表3 小波基‘db40’的實驗結果

表1～表3分別是3種常用的小波基分解3次后，按照融合指標方法和信噪比與信噪比增益方法分析得到的數據結果。由表中數據可知，隨著分解層數增加，按照融合方法得到的指標參數不斷減小；信噪比和信噪比增益不斷增大。因此，按照信噪比與信噪比增益的方法，應該選擇‘db40’為最優小波基；按照指標融合的方法，‘db40’小波也是最優小波選擇。也就是說，在非合作通信條件下，選取‘db40’小波為跳頻信號去噪的最優小波基。這個結果與已知信號真值情況下融合方法得到的結果一致。

通過仿真實驗發現，改進的最優小波基選取方法較多指標融合的小波去噪質量評價方法更加簡單迅速。

據此，本文選取‘db40’小波為跳頻信號小波去噪的小波基，并對跳頻信號進行檢測。實驗結果如圖1、圖2所示。

圖1 短時傅里葉變換

圖2 W-H算法

從仿真結果中可以看到，利用W-H算法檢測的跳頻信號在抗噪性與時頻聚集性兩方面的性能優于常用的短時傅里葉變換。同時也證明了改進的最優小波基選取方法在選取最優小波基方面有較好的性能。

7 結論

本文在小波分解與希爾伯特-黃變換的跳頻信號檢測方法的基礎上，對小波去噪過程中的最優小波基的選取作了深入研究。通過對分解過程中重構信號信噪比的盲估計，利用改進的信噪比與信噪比增益的方法對小波基進行篩選，解決了非合作通信條件下，傳統小波去噪質量評價方法因信號真值未知而無法使用的問題，對非合作通信條件下最佳小波基的選取問題提供了新的解決方案。同時將其應用到跳頻信號檢測中，仿真實驗證明了該方法極大地提高了跳頻信號檢測的性能。