橢偏高斯光束經過非線性介質后的遠場衍射圖樣

陶 智，彭楚楚，鄧羅根

(北京理工大學 物理學院，北京 100081)

1 引 言

高斯光束入射非線性介質后，由于介質的三階非線性效應會引起入射光相位分布發生變化，在遠場產生明暗相間的衍射圓環，該現象被稱為空間自相位調制現象。空間自相位調制現象由于其在材料非線性折射率的測量[1-2]、非線性光限幅器的設計[3]以及中空激光束的產生[4]等方面有著極大的應用價值而受到廣泛關注。最早由Callen等人[5]在實驗中觀察到。此后，人們相繼在液晶[6-8]、原子蒸汽[9]、聚合物[10]以及納米復合材料[11]等非線性材料系統中觀測到類似的現象，區別僅在于衍射環的數目不同、圖樣中心的斑點在一些實驗中是亮斑，而在另一些實驗中是暗斑。為了解釋這種環狀圖樣的形成機理，早在1981年Durbin等人[12]從空間自相位調制角度很好地解釋了實驗中出現的環狀衍射圖樣，并給出了衍射環數和最大附加相移間的定量關系。1997年，Harrison研究小組[13]在實驗中發現，當高斯光束經過一個薄的吸收型自散焦介質時，會在遠場形成中心恒為暗斑的衍射圖樣。次年，他們研究小組[14]利用耦合場物質方程對上述現象給出了理論分析，并得出結論，遠場暗斑的穩定存在是波前曲率和空間自相位調制共同作用的結果。2005年，Deng等人[15]系統研究了自聚焦、自散焦介質對發散、會聚高斯光束的作用，總結了不同遠場環狀圖樣出現的條件，他們認為當波前曲率和附加相移的乘積的符號為正時，遠場會出現中心是亮斑的環狀衍射條紋，而當波前曲率和附加相移的乘積的符號為負時，遠場衍射圖樣的中心是暗斑。此后，人們在研究工作中發現，樣品的位置[16]、介質的非局域性[17]、入射光場的頻率、能量等因素[18]均會對遠場衍射圖樣的形成產生影響。值得一提的是，盡管之前人們對空間自相位調制現象的研究取得了一系列成果，但是他們沒有考慮當入射非線性介質的光是偏振光時，非線性介質對不同偏振光響應的差別。事實上，早在上世紀60年代初，Maker等人[19]在研究液晶折射率隨強度變化的工作中就已指出，對于同一各向同性非線性介質，橢圓偏振光的左旋圓偏振分量和右旋圓偏振分量引起的非線性折射率不同。Boyd[20]也曾在書中明確給出線偏振光、圓偏振光以及橢圓偏振光在非線性介質中的非線性折射率的表達式。

本文以衍射理論為基礎，建立了偏振態為橢圓偏振的高斯光束(橢偏高斯光束)經過非線性介質后遠場光強分布的理論模型。采用數值方法，研究了橢偏高斯光束入射非線性介質后的遠場光強分布圖及衍射圖樣。進一步研究發現，入射光場的橢偏率是影響遠場光強分布的重要因素，并且非線性機制不同，橢偏率對遠場光強分布的影響也不同。

2 理 論

設橢偏高斯光束經過一個薄的線性吸收型各向同性非線性介質，那么，介質入射面上光場的瓊斯矢量可以表示為

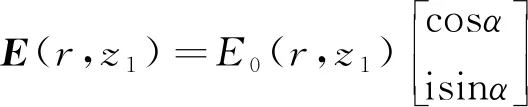
(1)

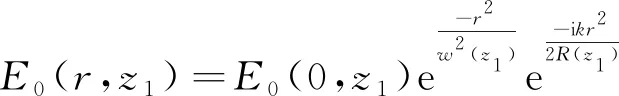
E(r,z1)=E+σ++E-σ-，

(2)

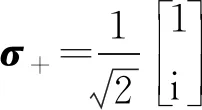
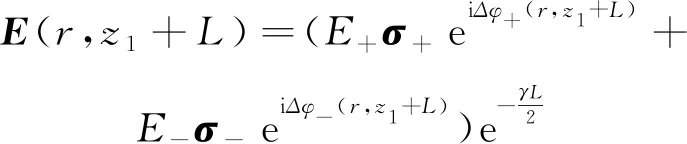
(3)

式中:γ為非線性介質的線性吸收系數，Δφ+(r,z1+L)和Δφ-(r,z1+L)分別代表左旋圓偏振光及右旋圓偏振光在介質出射面處對應的附加相移[15]，可分別表示為

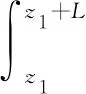
(4)

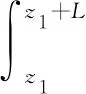
(5)

式中:Δn+和Δn-分別為左旋圓偏振光及右旋圓偏振光在非線性介質內對應的非線性折射率。由參考文獻[19]可知，

(6)

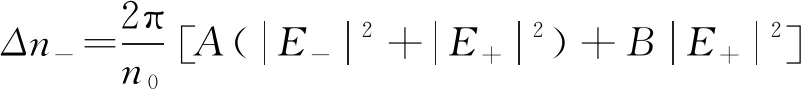
(7)

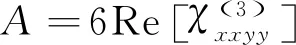
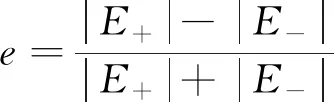
(8)

當e=0時，入射光為線偏振光；當e=1時，入射光為左旋圓偏振光；當e=-1時，入射光為右旋圓偏振光。此時，式(6)、(7)可統一表示為

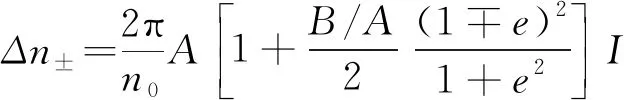
(9)

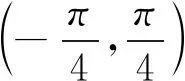
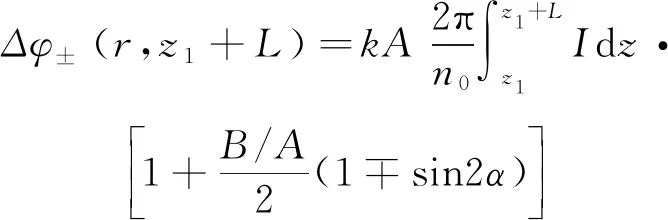
(10)

根據文獻[20]，式中B/A可代表引起非線性折射率的非線性機制，B/A=0代表電致伸縮或熱致非線性機制，B/A=1代表非共振電子非線性機制，B/A=6代表分子取向非線性機制。由朗伯(Lambert)定律可知,在介質內部，光強與z的關系可近似為

I(r,z)=I(r,z1)e-γ(z-z1)，

(11)

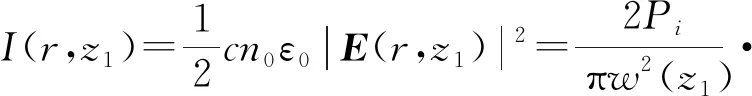
(12)

令

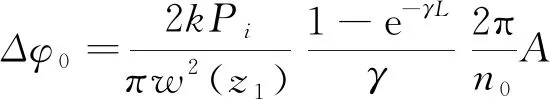
(13)

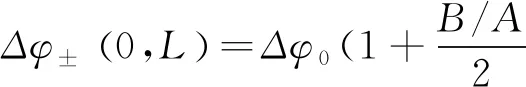
(14)

則式(12)可寫為

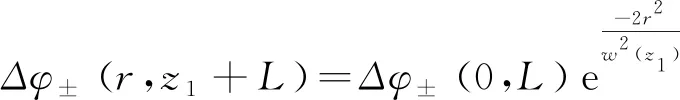
(15)

其中：Δφ±(0,L)表示介質位于z1位置時橢偏高斯光束在介質出射面產生的峰值非線性相移。Δφ0表示在B/A=0或入射光為圓偏振光的情況下產生的相移，本文中，我們稱它為“原相移”。利用基爾霍夫-夫瑯禾費遠場衍射公式[22]，我們可以得到遠場衍射后的場強為

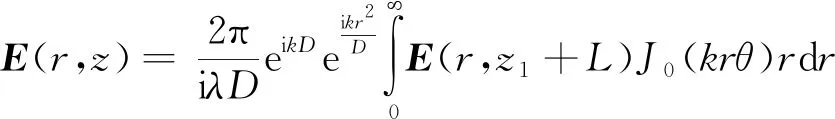
(16)

式中：J0(krθ)是第一類零階貝塞爾函數，D是樣品與觀察屏之間的距離。為積分方便，將E(r,z1+L)做正交分解，寫為兩個線偏振分量Ex和Ey的疊加形式，

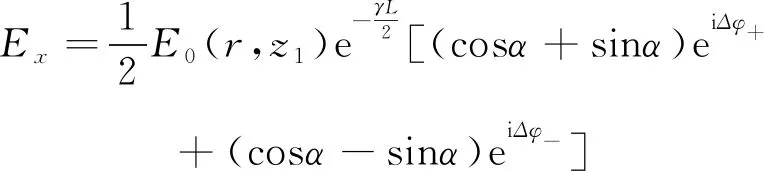
(17)

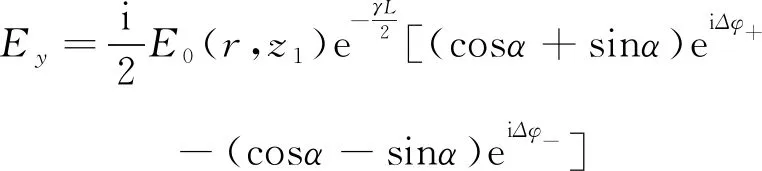
(18)

分別計算Ex和Ey在遠場的光強分布Ix和Iy，設遠場探測孔徑的半徑為ρ，考慮光強，則

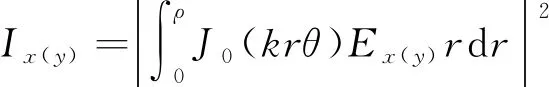
(19)

相應地，遠場衍射總光強I=Ix+Iy。

3 模擬結果及分析

以下我們將利用式(19)對橢偏高斯光束經過非線性介質后的遠場光強分布及衍射圖樣進行數值模擬。由理論部分可知，橢偏率e是影響橢偏高斯光束經過非線性介質后的遠場衍射圖樣的一個重要因素，本文將著重探究其在遠場衍射圖樣形成過程中的作用。模擬程序中所選固定參數為λ=532 nm，w(z1)=1 mm，Δφ0=4π，R(z1)=2 m。

圖1(a)、(c)、(e)是在電致伸縮非線性機制或熱致非線性機制(對應于參數B/A=0)情況下，橢偏率e分別取0.4，0.6，0.8時橢偏高斯光束通過非線性介質后的遠場光強分布圖，橫坐標表示遠場衍射角，縱坐標表示光強。圖1(b)、(d)、(f)是與圖1(a)、(c)、(e)相對應的遠場衍射圖樣。模擬結果顯示，在電致伸縮非線性機制下，遠場光強的x分量對總光強的貢獻隨著橢偏率e的增大而減小，y分量的貢獻隨橢偏率的增大而增大。二分量疊加后，遠場總光強的分布不隨橢偏率的改變而改變。總光強最亮環的光強約為0.97，中心暗斑的光強約為0.11。相應地，不同橢偏率的橢偏高斯光束入射非線性介質在遠場形成的衍射圖幾乎樣完全相同，如圖1(b)、(d)、(f)所示。圖樣中心均為暗斑，暗斑外圍均有3個亮環，2個暗環，且最外側的亮環光強強度最大。該現象說明，當引起介質非線性折射率的機制是電致伸縮非線性機制時，橢偏率對遠場衍射光強分布的影響可忽略不計。

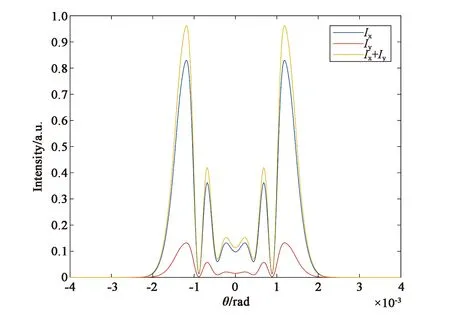
(a) e=0.4時的遠場光強分布圖(a) Far-field intensity distribution with e=0.4

(b) e=0.4時的遠場衍射圖樣(b) Far-field diffraction pattern with e=0.4

(c) e=0.6時的遠場光強分布圖(c) Far-field intensity distribution with e=0.6

(d) e=0.6時的遠場衍射圖樣(d) Far-field diffraction pattern with e=0.6

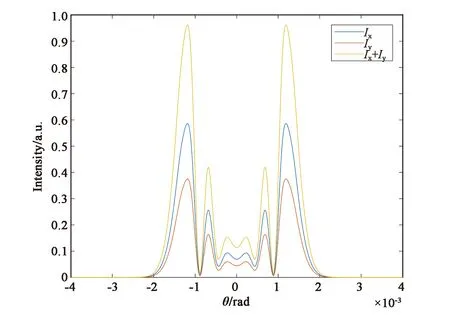
(e) e=0.8時的遠場光強分布圖(e) Far-field intensity distribution with e=0.8

(f) e=0.8時的遠場衍射圖樣(f) Far-field diffraction pattern with e=0.8圖1 B/A=0時，不同橢偏率下的遠場光強分布圖和遠場衍射圖樣。Fig.1 Far-field intensity distribution and far-field diffraction pattern with different ellipticity while B/A=0

圖2(a)、(c)、(e)是在非共振電子非線性機制(對應于參數B/A=1)情況下，橢偏率e分別取0.4，0.6，0.8時橢偏高斯光束通過非線性介質后的遠場光強分布圖。從圖中可以看到，在非共振電子非線性機制下，隨著橢偏率的增大，x分量和y分量發生同步變化，表現為光場分布半徑變小，中心斑點半徑變小，中心斑點外圍最亮環的光強變強。總光強隨之發生相同的變化。e=0.4時，總光強的光場半徑約為e=0.8時的1.5倍。e=0.4時，總光強最亮環的光強最小，約為0.68。e=0.6時，最亮環光強約降為0.80。e=0.8時，總光強最亮環的光強最大，約為0.95。由此可知，當引起介質非線性折射率的機制是非共振電子非線性機制時，橢偏率的增大會導致遠場光強分布半徑和中心斑點分布半徑變小，光能更多地分布在衍射外環。圖2(b)、(d)、(f)是與圖2(a)、(c)、(e)相對應的遠場衍射圖樣。

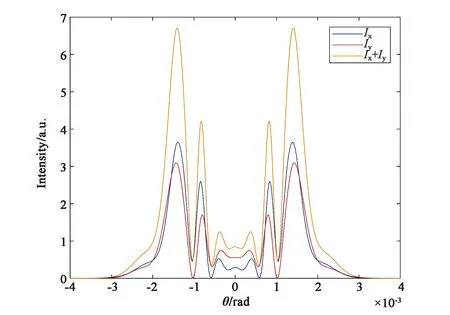
(a) e=0.4時的遠場光強分布圖(a) Far-field intensity distribution with e=0.4

(b) e=0.4時的遠場衍射圖樣(b) Far-field diffraction pattern with e=0.4

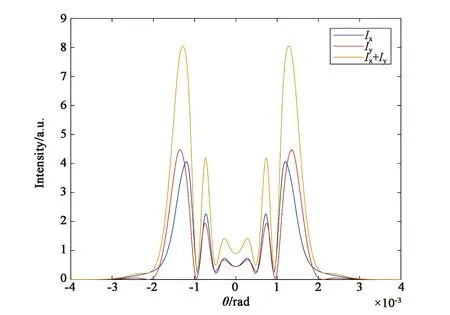
(c) e=0.6時的遠場光強分布圖(c) Far-field intensity distribution with e=0.6

(d) e=0.6時的遠場衍射圖樣(d) Far-field diffraction pattern with e=0.6

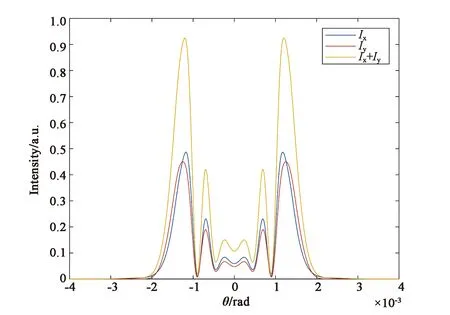
(e) e=0.8時的遠場光強分布圖(e) Far-field intensity distribution with e=0.8

(f) e=0.8時的遠場衍射圖樣(f) Far-field diffraction pattern with e=0.8圖2 B/A=1時，不同橢偏率下的遠場光強分布圖和遠場衍射圖樣。Fig.2 Far-field intensity distribution and far-field diffraction patterns with different ellipticity while B/A=1

圖3是分子取向非線性機制(對應于參數B/A=6)情況下，不同橢偏率的橢偏高斯光束通過非線性介質后的遠場光強分布圖及衍射圖樣。從圖中可以看到，當e=0.4時，總光強的分布與二分量的光強分布一致，中央光斑均為亮斑，且中心光強最強，約為1.27。中心外圍有4個亮環，4個暗環。當e=0.6時，x光強分量與y光強分量中心光強最強。相應地，總光強的中心光強也最強，約為1.27。然而，此時，總光強中心斑點外圍的衍射亮環和暗環較e=0.4時均減少1個，并且光場分布半徑變小。當e增大至0.8時，二分量的分布半徑繼續減小，衍射暗環數目減少，中心光強變弱，最外衍射環的光強最強。此時，總光強的分布隨之發生同步變化。圖(b)、(d)、(f)為圖(a)、(c)、(e)各自對應的遠場衍射圖樣，從衍射圖樣可以明顯看到，當B/A=6時，橢偏率的增大不僅會影響圖樣的分布尺寸和衍射環數目，還會影響圖樣中心斑點的亮暗。

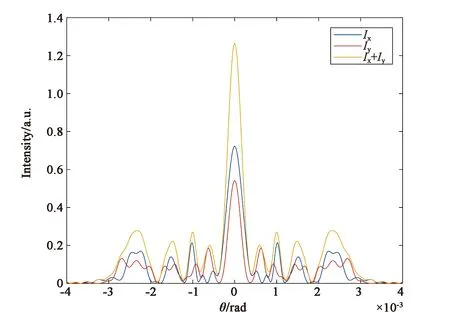
(a) e=0.4時的遠場光強分布圖(a) Far-field intensity distribution with e=0.4

(b) e=0.4時的遠場衍射圖樣(b) Far-field diffraction pattern with e=0.4

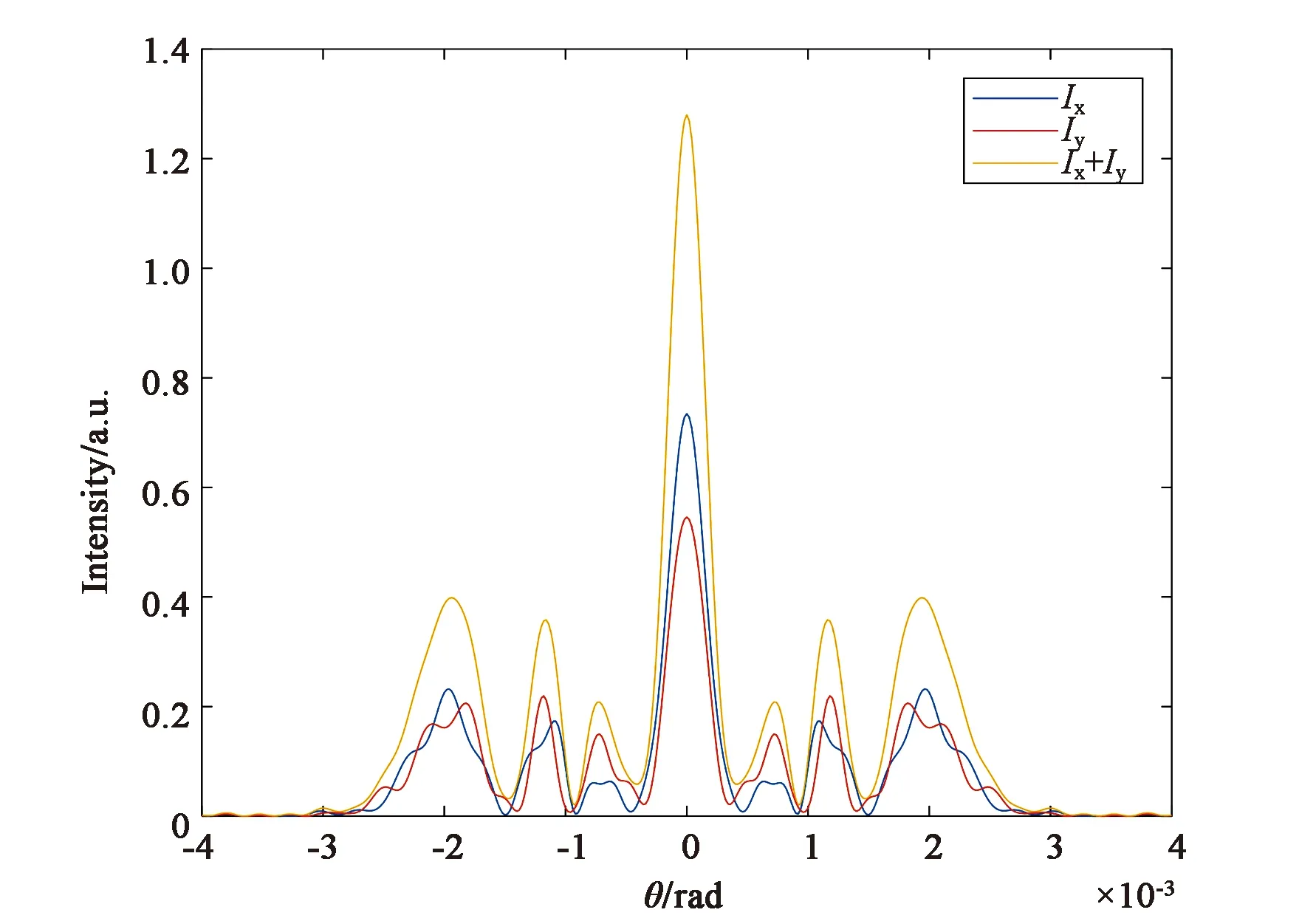
(c) e=0.6時的遠場光強分布圖(c) Far-field intensity distribution with e=0.6

(d) e=0.6時的遠場衍射圖樣(d) Far-field diffraction pattern with e=0.6

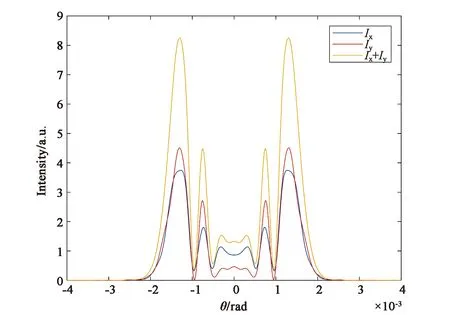
(e) e=0.8時的遠場光強分布圖(e) The far-field intensity distribution with e=0.8

(f) e=0.8時的遠場衍射圖樣(f) Far-field diffraction pattern with e=0.8圖3 B/A=6時，不同橢偏率下的遠場光強分布圖和遠場衍射圖樣。Fig.3 Far-field intensity distribution and far-field diffraction patterns with different ellipticity while B/A=6

綜上可知，橢偏率的改變會導致遠場衍射圖樣的直徑、衍射環數以及中心斑點的亮暗發生變化。在不同的非線性機制下，橢偏率的改變會對遠場衍射圖樣產生不同的影響，影響程度的大小隨非線性機制對應的B/A數值的增大而增大。在電致伸縮或熱致非線性機制下，遠場衍射圖樣幾乎不隨橢偏率的改變而改變，橢偏率的改變對圖樣產生的影響可忽略不計。在非共振電子響應非線性機制和分子取向非線性機制下，橢偏率的增大會導致遠場衍射圖樣分布尺寸變小。相比之下，當引起非介質折射率變化的機制是分子取向非線性機制時，遠場光強分布對入射光場橢偏率改變的響應更敏感，遠場衍射圖樣的衍射環數和中心斑點的亮暗均會隨橢偏率的改變發生明顯變化。

4 結 論

綜上所述，我們可以得到以下結論：本文建立的計算遠場光強分布的理論模型不僅適用于橢偏高斯光束入射非線性介質的情形，通過改變橢偏率e值的大小，還可以得到入射光偏振態為線偏振態、圓偏振態時遠場光強的分布模型。處于不同非線性機制下的非線性材料對入射橢偏激光橢偏率變化的響應不同。電致伸縮非線性機制下，橢偏率的變化對橢偏高斯光束經過非線性介質后的遠場衍射圖樣的影響可忽略不計；非共振電子響應非線性機制下，隨著橢偏率的增大，遠場衍射圖樣的半徑變小、中央光斑半徑變小、光場能量更多地分布在衍射外環；分子取向非線性機制下，隨著橢偏率的增大，遠場衍射圖樣的半徑變小、衍射環數變少、中心斑點由亮斑變為暗斑。根據衍射圖樣隨不同非線性機制的不同演化特征，可以有效區分在強光與非線性介質的相互作用中處于主導位置的非線性機制類型。該結論對非線性機制類型的判斷和光限幅器件的設計具有參考意義。