低階修正的Hotine截斷核函數的頻譜分析與應用

馬 健，魏子卿，任紅飛

1. 地理信息工程國家重點實驗室，陜西 西安 710054； 2. 西安測繪研究所，陜西 西安 710054； 3. 信息工程大學地理空間信息學院，河南 鄭州 450001

Stokes/Hotine積分是計算(似)大地水準面的理論工具[1-6]。Stokes/Hotine積分理論上需要全球積分，但由于全球重力數據難以獲取，且全球積分計算量較大，因此實際計算通常使用移去恢復技術，此時邊值解算僅需進行近區Stokes/Hotine積分。為了減弱遠區影響、提高(似)大地水準面的解算精度，出現了眾多核函數的修正方法。核函數修正方法可分為確定性修正與隨機性修正兩類。確定性修正理論包括有Meissl方法[7]、Molodensky方法、Sj?berg方法[8]、Wong和Gore方法等[9-10]，隨機性修正需將模型重力數據和實測重力數據的誤差階方差作為先驗信息，而實測數據的誤差階方差信息很難獲取，限制了隨機性修正方法的應用[11]。

使用移去恢復技術時需選定一個模型重力場作為參考場，因此Stokes/Hotine積分中包含了實測重力和模型重力兩類重力數據。重力測量、水準測量、地形歸算[12-13]、格網化[14]等使Stokes/Hotine積分中的實測重力數據存在一定的長波誤差[15]，而重力場模型的長波精度較高(satellite-only衛星重力場模型的前20階已達到非常高的精度[16-17])，因此Stokes/Hotine積分時，應選擇對實測重力數據具有高通濾波屬性的積分核函數。截斷核函數(the spheroidal kernel，由標準核函數除去一定階數的Legendre多項式得到)是一種非常有效的高通濾波器[18]，可有效地避免實測重力數據的長波誤差傳播到(似)大地水準面中，因此在基于移去恢復的邊值解算中應用較為廣泛。但模型重力數據的累積誤差隨著模型階數的增加而增大，而實測重力數據的中高頻誤差相對較小，因此為了獲得高精度的(似)大地水準面不宜過濾過多頻段的實測重力信息。

傳統積分核函數的研究主要為了減小遠區截斷誤差，但在移去恢復模式下，積分核對邊值解算精度的影響方式發生了轉變：在高頻波段(大于模型重力場截止階數的頻率波段)，核函數決定了高頻遠區截斷誤差的大小以及譜泄露的程度；在低頻波段(小于模型重力場截止階數的頻率波段)，核函數決定了實測與模型兩類重力數據對低階高程異常/大地水準面高的貢獻率。因此，在移去恢復模式中核函數的研究應分高頻和低頻兩個頻段展開。

Stokes積分核與Hotine積分核[19-21]具有相似的頻譜特性，Stokes核函數理論可方便地應用于Hotine積分核，反之亦然。根據Stokes-Helmert理論方法構建的加拿大重力大地水準面CGG2010[22]使用了高低階均修正的截斷Stokes核函數。本文以Hotine積分核為例在其基礎上提出了更加高效的低階修正的截斷核函數，不僅包括余弦低階修正核函數，還構造了一種線型低階修正核函數。本文首先對擴展Hotine核函數展開頻譜分析，然后根據Hotine-Helmert理論方法使用不同的Hotine核函數解算了試驗區的似大地水準面，以驗證不同Hotine核函數的應用效果。

1 Hotine截斷核函數

在移去恢復模式下，使用傳統截斷Hotine核函數計算高程異常(高程異常為似大地水準面到參考橢球面的距離)的算法公式為

(1)

式中，ζ為高程異常；ζM為模型高程異常；C1為Hotine的近區積分范圍；R為地球平均半徑；r為計算點的地心向徑；γ為地面點的正常重力；ψ為流動點與計算點間的球心角距；δgT為地面重力擾動；δgM為模型重力擾動；*表示向下延拓過程[23-26]，通過向下延拓可將地面重力值轉化為邊界面重力值；Hbl(r,ψ)為擴展形式的Hotine截斷核函數，為方便表述下文省略“擴展”。

目前廣泛使用的Hotine截斷核函數有兩種。一種是高低階均截斷的核函數

(2)

式中，L為低階截斷頻率(階數)；M為由地形分辨率決定的高階截斷頻率；Pn(cosψ)為Legendre函數。另一種為僅低階截斷的核函數

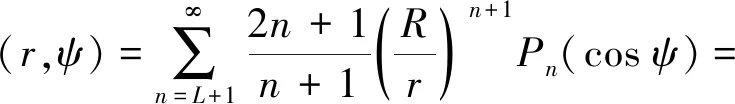
(3)

式中，Hstd為標準形式的Hotine積分核

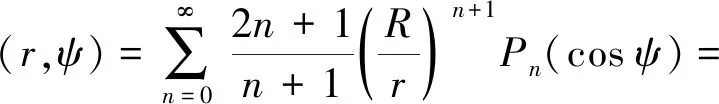
(4)

2 修正的Hotine截斷核函數

修正的截斷核函數是通過對傳統截斷核函數增加修正因子得到的，即

(5)

式中,αn為修正因子，也可稱為平滑因子。

2.1 高低階均修正

文獻[22]提出了余弦函數構建的高低階均修正的截斷核函數，其修正因子為

(6)

式中，μ為低階修正帶寬；υ為高階修正帶寬，修正帶寬表示修正的階數區間。從式(6)可以看出該修正因子在L-μ階到L階的頻率波段從0逐漸增大至1，在M階到M+υ階的頻率波段由1逐漸減少至0。當修正區間(L-μ,L)和(M,M+υ)的各階修正因子均取0時，高低階均修正的截斷核函數轉化為式(2)所示的傳統高低階均截斷的核函數。

由于邊值解算采用的重力數據、地形數據均為離散的網格數據，因而需對Hotine積分進行離散化。當對中央網格(計算點地心向徑穿過的網格)進行離散化時，通常將中央網格近似為圓形區域。采用高低階均修正的Hotine截斷核函數時，通過推導可得出中央網格重力擾動對高程異常貢獻ζ0的近似公式為

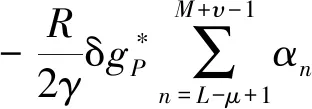
(7)

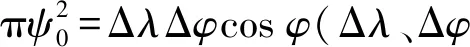
2.2 低階修正

本文在高低階均修正的截斷核函數的基礎上提出了僅低階修正的截斷核函數，兩種修正核函數的差別在于修正因子的不同。低階修正的截斷核函數的修正因子αn為

(8)

從式(8)可看出，低階修正核函數的修正因子在L-μ階到L階的頻率區間由0逐步增大至1。當低階修正頻率區間(L-μ,L)的各階修正因子均取0時，低階修正核函數轉化為傳統僅低階截斷的核函數。式(8)所示的低階修正核函數的修正因子是由余弦函數構造的。本文進一步提出一種線型低階修正的核函數，其修正因子為

(9)

式(9)所示的線型低階修正核函數的修正因子同樣具有在L-μ階至L階的頻段由0逐步增大至1的特點。圖1為兩種低階修正核函數的修正因子的取值。

由圖1可知，對于余弦修正核函數，修正因子在修正初始頻段和修正末尾頻段變化相對較慢，而在修正的中間頻段變化相對較快；對于線型低階修正核函數，修正因子在修正頻段保持固定的變化速度。修正因子的類型及參數設置與實測重力數據和模型重力數據的相對精度有關。當使用低階修正的Hotine截斷核函數時，通過推導可得出中央網格重力擾動對高程異常貢獻ζ0為

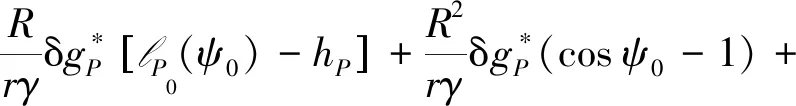
(10)

式中，lP0(ψ0)的計算公式為

3 移去恢復模式下Hotine積分的譜分解式

在移去恢復模式下，Hotine積分僅需近區積分。根據勒讓德函數的球面積分算法和Molodensky截斷理論，近區Hotine積分可表示為如下譜形式

(11)

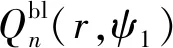
(12)

式(11)、式(12)不僅適用于修正形式的Hotine截斷核函數，對于傳統Hotine截斷核函數也是適用的，此時αn只有0和1兩種取值(傳統Hotine截斷核函數為修正Hotine截斷核函數的特例)。根據式(11)所示的譜表示方法可對式(1)進行如下改化

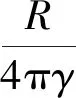
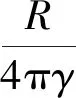
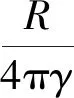
(13)

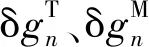
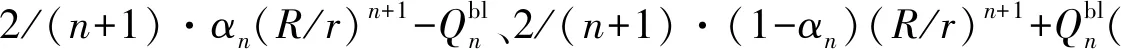
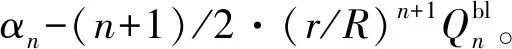
4 試驗與分析

4.1 頻譜分析

根據上文分析，在移去恢復模式下核函數在高、低頻波段對高程異常的影響方式不同，因此對核函數的頻譜分析應分高、低頻兩個波段進行。本節頻譜分析過程中將計算點高程設為1000 m，Hotine積分半徑設為1°，低、高階截斷頻率(階數)分別取為360、5400。圖2為使用不同的Hotine核函數時實測重力數據對高程異常的高階貢獻率，其中修正因子采用余弦函數形式，低、高階修正帶寬均為180階。

根據圖2，在高頻波段的初始頻段，高低階均截斷與低階截斷的Hotine核函數對高程異常的高階貢獻率差異很小，而高低階均修正與僅低階修正的Hotine核函數的高階貢獻率的差異也非常小。貢獻率越接近1，重力數據越能夠有效地傳播到解算的高程異常中。圖2中傳統截斷核函數在高頻波段的初始頻段貢獻率較低，說明傳統截斷核函數存在較嚴重的譜泄露現象。修正的截斷核函數能夠有效地控制譜泄露現象，提高了實測數據在高頻波段初始頻段的貢獻率。在高階截斷頻率附近，幾種核函數中高低階均截斷的核函數存在比較明顯的譜泄露現象。圖3為使用不同的Hotine核函數時模型和實測數據對高程異常的低階貢獻率。

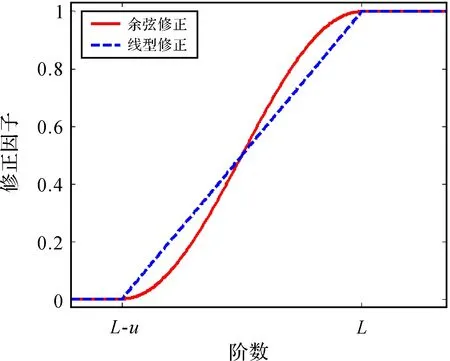
圖1 兩種修正因子的取值Fig.1 Values of the two modification factors

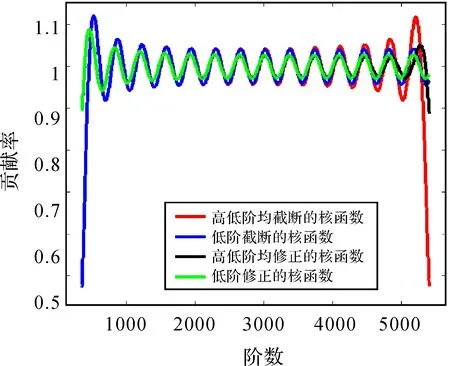
圖2 實測數據的高階貢獻率Fig.2 High-degree contribution rates of the measured data

圖3 模型和實測數據的低階貢獻率Fig.3 Low-degree contribution rates of the measured data and model data

從圖3可以看出，在低頻波段，兩種截斷Hotine核函數的低階貢獻率差異很小，兩種修正Hotine核函數的低階貢獻率差異也很小。在低頻波段的初始頻段，使用截斷和修正形式的核函數時模型數據的貢獻率均接近1，說明在低頻波段的初始頻段高程異常主要來自模型數據的貢獻。在修正頻段(L-μ～L，此處為180～360)，使用修正核函數時實測數據對高程異常的貢獻多于使用傳統截斷核函數時實測數據對高程異常的貢獻。

下面分析不同修正帶寬下實測和模型數據對高程異常的貢獻率的變化，使用的核函數分別為余弦低階修正和線型低階修正的Hotine截斷核函數。圖4所示為不同修正帶寬下實測數據的高階貢獻率。

圖4 不同修正帶寬下實測數據的高階貢獻率Fig.4 High-degree contribution rates of the measured data using different modification bandwidths

由圖4可知，在高頻波段的初始頻段，對于兩種(余弦與線型)低階修正的Hotine核函數，低階修正帶寬為90階時實測重力數據的貢獻率均明顯小于修正帶寬為180、270、360階時的貢獻率，說明90階修正帶寬下兩種低階修正核函數對譜泄露現象的改善程度不及180、270、360階修正帶寬下修正核函數對譜泄露的改善程度。圖4中，使用余弦與線型低階修正核函數時實測重力數據的高階貢獻率相差不大，但當修正帶寬為360階時，使用線型低階修正核函數時實測重力數據的高階貢獻率更接近1，說明此時線型低階修正核函數稍優于余弦低階修正核函數。圖5所示為不同修正帶寬下模型和實測重力數據的低階貢獻率。

圖5 不同修正帶寬下實測和模型數據的低階貢獻率Fig.5 Low-degree contribution rates of the measured data and model data using different modification bandwidths

從圖5可以看出，使用兩種低階修正核函數時實測與模型重力數據對低階高程異常的貢獻率相差不大。在未修正的頻率區間(0～L-μ)，低階高程異常的貢獻主要來自于模型重力擾動；在修正的頻率區間(L-μ～L)，實測重力擾動的貢獻逐漸增大，而模型重力擾動的貢獻逐漸減少。從圖5中還可看出，修正帶寬越大，模型重力數據的貢獻越少而實測重力數據的貢獻越多，因此可通過調整修正帶寬控制實測和模型重力數據對低階高程異常貢獻的權重。

4.2 應用試驗

為了說明不同Hotine核函數的應用效果，針對不同形式的Hotine核函數解算似大地水準面進行了試驗。似大地水準面的區域范圍為108°E—114°E，28°N—32°N，該區域海拔最高2700 m，平均607 m。本試驗收集了105.5°E—116.5°E，25.5°N—34.5°N范圍內的70 822個地面離散重力點，剔除粗差后，將剩余的70 379個實測重力點作為邊值解算的基礎重力數據。本試驗邊值解算采用基于移去恢復的Hotine-Helmert理論方法[27]，其中地形直接、間接影響采用文獻[28]給出的算法公式。試驗區共有68個GPS水準點，利用試驗區GPS水準點對截斷至360階和2190階的EIGEN-6C4、EGM2008重力場模型分別進行精度檢核，其結果統計于表1。

表1 截斷到不同階數的重力場模型精度

Tab.1 Accuracies of the gravity field models with different cutoff degreesm

表1中，截斷到360和2190階的EIGEN-6C4模型精度(標準差)分別為±28.2 cm與±7.8 cm，而截斷到360和2190階的EGM2008模型精度分別為±29.5 cm與±10.6 cm，由此可看出試驗區EIGEN-6C4模型精度優于EGM2008模型。

下面首先利用兩種截斷(高低階均截斷、低階截斷)Hotine核函數計算似大地水準面，為了提高計算速度，本試驗采用2′×2′的格網分辨率。表2統計了解算的重力似大地水準面的精度與Hotine積分所需時間，其中Hotine積分半徑為1°，高階截斷階數取5400階(根據Nyquist采樣定律可知2′×2′分辨率格網對應5400階的高階截斷頻率)，低階截斷階數取360，參考模型取EIGEN-6C4模型的前360階。

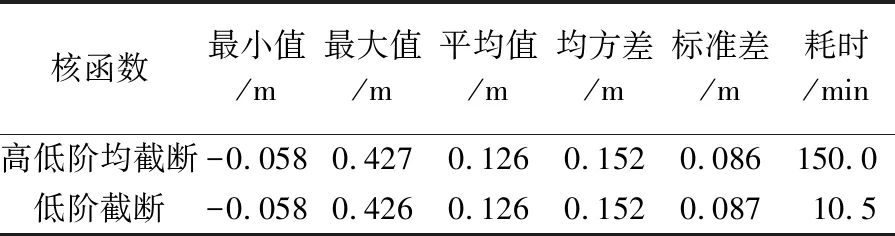
表2 兩種傳統截斷核函數計算的重力似大地水準面精度

Tab.2 Accuracies of the gravimetric quasi-geoids using the two traditional spheroidal kernels

核函數最小值/m最大值/m平均值/m均方差/m標準差/m耗時/min高低階均截斷-0.0580.4270.1260.1520.086150.0低階截斷-0.0580.4260.1260.1520.08710.5

從表2可以看出，兩種傳統截斷核函數計算的似大地水準面精度基本沒有差別，但圖2中兩種傳統截斷核函數在高階截斷頻率附近差異較大，這反映了高程異常對高頻信息不敏感的頻譜特性。根據表2，在解算精度一致的前提下，使用低階截斷核函數時Hotine積分所需的計算時間較高低階均截斷的核函數明顯縮短，因此對于兩種截斷核函數，低階截斷的核函數比高低階均截斷的核函數更適于邊值解算。

表3比較了兩種修正(高低階均修正、低階修正)Hotine核函數在邊值解算精度與計算時間上的差別，其中低階修正帶寬取180階，高階修正帶寬分別取180、540階，修正核函數采用余弦修正形式，其他參數設置與表2相同。

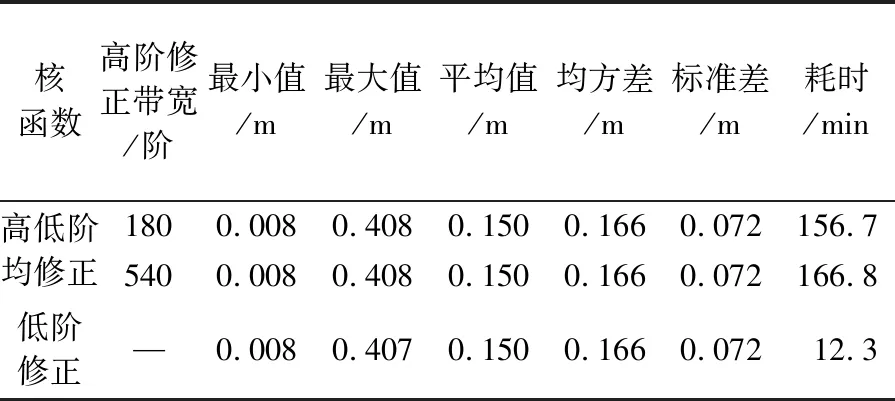
表3 兩種修正核函數計算的重力似大地水準面精度

Tab.3 Accuracies of the gravimetric quasi-geoids using the two modified spheroidal kernels

核函數高階修正帶寬/階最小值/m最大值/m平均值/m均方差/m標準差/m耗時/min高低階均修正1800.0080.4080.1500.1660.072156.75400.0080.4080.1500.1660.072166.8低階修正—0.0080.4070.1500.1660.07212.3

從表3可得出，當低階修正帶寬一定時，兩種修正核函數解算的似大地水準面的精度基本相同。另外還可看出，高階修正帶寬對似大地水準面的精度的影響非常小。由于低階修正核函數較高低階均修正核函數大大縮短了計算時間，而二者的計算精度相同，因此低階修正的核函數比高低階均修正的核函數更適于邊值解算。此外，對比表2、表3可看出，低階修正核函數計算的似大地水準面精度優于低階截斷核函數的計算精度，二者在計算效率方面的差別也不大，因此低階修正的截斷核函數的應用效果優于其他核函數。

為了說明低階修正帶寬對邊值解算精度的影響，表4統計了使用不同的低階修正帶寬時求解的重力似大地水準面的精度，其中低階修正核函數采用余弦修正形式，地形分辨率為1.5′×1.5′，Hotine積分半徑為1°，同樣以EIGEN-6C4重力場模型的前360階作為參考模型。

表4 余弦低階修正核函數計算的重力似大地水準面的精度

Tab.4 Accuracies of the gravimetric quasi-geoids using the cosine low-degree modified kernels

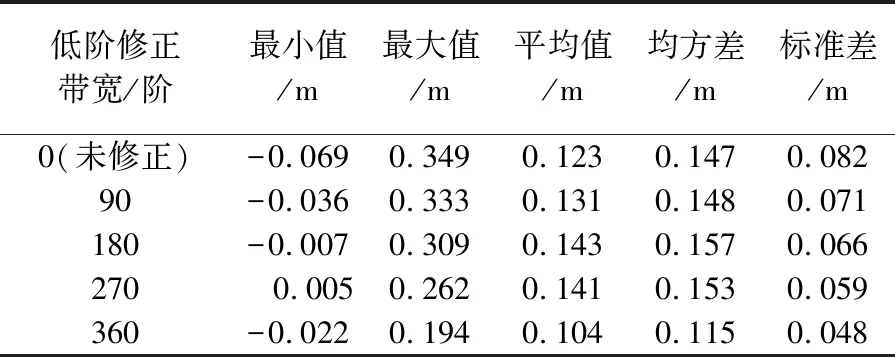
低階修正帶寬/階最小值/m最大值/m平均值/m均方差/m標準差/m0(未修正)-0.0690.3490.1230.1470.08290-0.0360.3330.1310.1480.071180-0.0070.3090.1430.1570.066270 0.0050.2620.1410.1530.059360-0.0220.1940.1040.1150.048

低階修正帶寬取0時低階修正核函數實際即為傳統的低階截斷核函數。從表4可知，低階修正帶寬對似大地水準面的精度具有較大的影響。在本文試驗區360階低階修正帶寬解算的似大地水準面精度最高(±4.8 cm)，而傳統截斷核函數計算的似大地水準面精度僅為±8.2 cm。似大地水準面精度的提高一方面是由于低階修正核函數有效地控制了傳統截斷核函數存在的譜泄露問題，另一方面是由于低階修正核函數增大了實測重力數據在低階修正頻段對高程異常的貢獻。

表5統計了不同低階修正帶寬下線型低階修正Hotine核函數計算的重力似大地水準面精度，其參數設置同表4。

表5 線型低階修正核函數計算的重力似大地水準面的精度

Tab.5 Accuracies of the gravimetric quasi-geoids using the linear low-degree modified kernels

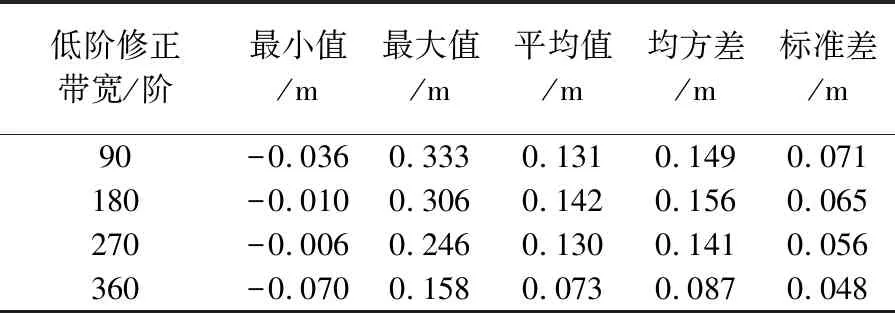
低階修正帶寬/階最小值/m最大值/m平均值/m均方差/m標準差/m90-0.0360.3330.1310.1490.071180-0.0100.3060.1420.1560.065270-0.0060.2460.1300.1410.056360-0.0700.1580.0730.0870.048

比較表4、表5可知，在相同的低階修正帶寬下，線型低階修正與余弦低階修正核函數計算的似大地水準面精度基本一致。將表4、表5的結果與表2進行比較可以看出低階修正核函數的應用效果較好。

由于不同重力場模型的精度不同，而修正帶寬起到調整模型和實測重力數據在高程異常中貢獻的比重的作用，因此使用不同的參考模型時適宜的低階修正帶寬也存在差異。為此，表6統計了以EIGEN-6C4模型與EGM2008模型的前360階作為參考模型時不同低階截斷階數下適宜的低階修正帶寬(即使用該低階修正帶寬時邊值解算精度相對較高)及相應的似大地水準面精度，其中核函數采用余弦低階修正核函數。

表6 以重力場模型的前360階作為參考模型時解算的重力似大地水準面精度

Tab.6 Accuracies of the gravimetric quasi-geoids with the first 360 degrees of the gravity field model as the reference field

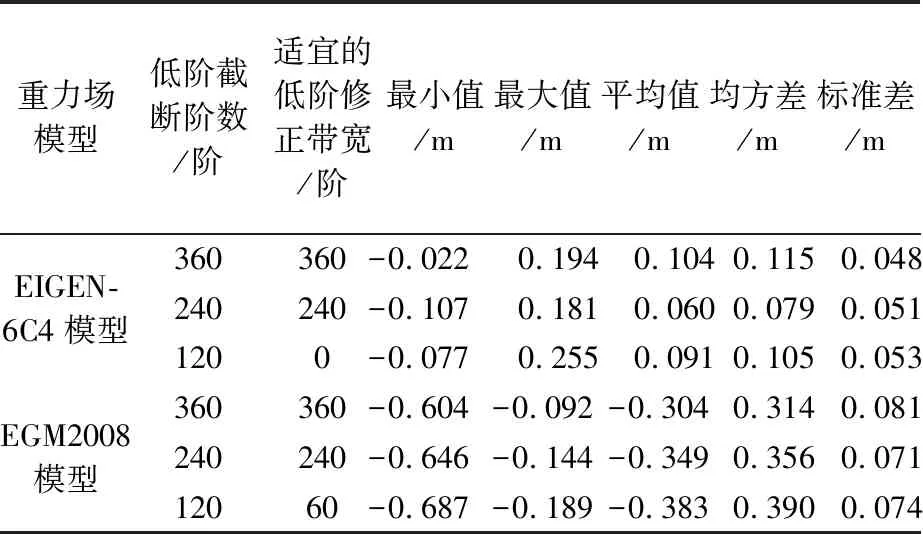
重力場模型低階截斷階數/階適宜的低階修正帶寬/階最小值/m最大值/m平均值/m均方差/m標準差/mEIGEN-6C4模型360360-0.022 0.194 0.104 0.115 0.048240240-0.1070.1810.0600.0790.0511200-0.0770.2550.0910.1050.053EGM2008模型360360-0.604 -0.092 -0.304 0.314 0.081240240-0.646-0.144-0.3490.3560.07112060-0.687-0.189-0.3830.3900.074

表6中，當以EIGEN-6C4模型的前360階作為參考模型時，低階截斷階數與低階修正帶寬均取360解算的似大地水準面精度最高(±4.8 cm)，而當低階截斷階數取120時，核函數不進行修正時邊值解算精度相對較高。當以EGM2008模型的前360階作為參考模型時，低階截斷階數與低階修正帶寬均取240解算的似大地水準面精度最高(±7.1 cm)，但不及以EIGEN-6C4模型的前360階作為參考模型的邊值解算精度。

表7統計了采用2190階的EIGEN-6C4模型與EGM2008模型作為參考模型時，不同低階截斷階數下適宜的低階修正帶寬及相應的似大地水準面精度。

表7中，當以2190階的EIGEN-6C4模型與EGM2008模型作為參考模型時，低階截斷階數取2190階計算的似大地水準面精度并不理想。根據上文頻譜分析可知，當低階截斷階數取2190階時解算的高程異常主要來自于模型數據的貢獻，因此不能有效地利用實測數據的信息。當2190階EIGEN-6C4模型作為參考場時邊值解算精度(最高達±4.5 cm)優于2190階EGM2008模型作為參考場時邊值解算精度(最高達±6.8 cm)。對比表6可以看出，以2190階EIGEN-6C4模型作為參考模型較以360階EIGEN-6C4模型作為參考模型求解的似大地水準面的精度提高不明顯(分別為±4.5 cm與±4.8 cm)，這反映了遠區高程異常的高頻(361～2190階頻段)信息非常少。

表7 以2190階重力場模型作為參考模型解算的似大地水準面精度

Tab.7 Accuracies of the gravimetric quasi-geoids with the 2190 degree gravity field model as the referencefield

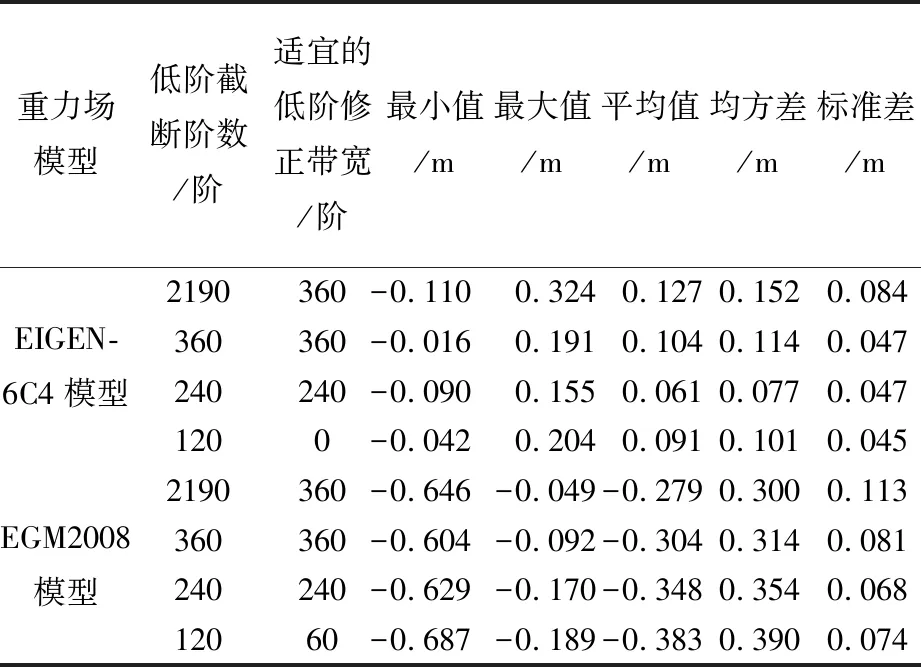
重力場模型低階截斷階數/階適宜的低階修正帶寬/階最小值/m最大值/m平均值/m均方差/m標準差/mEIGEN-6C4模型2190360-0.1100.3240.1270.1520.084360360-0.0160.1910.1040.1140.047240240-0.0900.1550.0610.0770.0471200-0.0420.2040.0910.1010.045EGM2008模型2190360-0.646-0.049-0.2790.3000.113360360-0.604-0.092-0.3040.3140.081240240-0.629-0.170-0.3480.3540.06812060-0.687-0.189-0.3830.3900.074

5 結 論

利用基于移去恢復技術的Stokes-Helmert邊值理論或Hotine-Helmert邊值理論求解(似)大地水準面時，截斷形式的Stokes/Hotine核函數是一種有效的高通濾波器。但傳統的截斷核函數存在譜泄露現象，影響了(似)大地水準面的解算精度，因此本文引入并進一步發展了一種低階修正的截斷核函數。本文的創新點與結論主要有：

(1) 在余弦函數構造的高低階均修正的核函數的基礎上提出了余弦低階修正核函數，進一步提出了線型低階修正核函數，并給出了使用高低階均修正核函數與低階修正核函數時Hotine積分的中央區算法。

(2) 對移去恢復模式下核函數在解算似大地水準面中的作用進行了頻譜分析，說明了在移去恢復模式下核函數研究的內容及內涵已發生轉變：在高頻波段，核函數影響著高頻遠區截斷誤差的大小以及譜泄露的程度，但在低頻波段，核函數決定了實測重力數據與模型重力數據對高程異常的貢獻率。通過對不同核函數的頻譜分析得出，修正核函數能夠有效地控制譜泄露現象，并且增大了實測數據在修正頻段對高程異常的貢獻率。余弦低階修正與線型低階修正核函數的頻譜特性比較接近。

(3) 試驗結果表明，采用相同的低階修正帶寬時，線型和余弦低階修正的核函數計算的似大地水準面精度與高低階均修正的核函數的計算精度一致，均優于傳統截斷核函數計算的似大地水準面精度。在計算效率上，低階修正的核函數明顯優于高低階均修正的核函數。

(4) 通過本文的試驗可看出，在基于Helmert第二壓縮法的邊值問題中低階修正的截斷核函數能夠有效地改善邊值解算的精度，具體應用時應結合參考模型精度、試驗區實測重力數據精度、模型截止階數等因素確定適宜的低階截斷階數以及低階修正帶寬。

本文的研究是對文獻[29]提出的厘米級精度要求下重新研究核函數的改進和構造截斷函數問題進行的理論探索與實踐，在Stokes-Helmert/Hotine-Helmert邊值理論的研究和應用方面具有一定的參考價值。