一種導出R-H準則的方法*

陳紹榮，李曉毅，何 為，王 開

（陸軍工程大學通信士官學校，重慶 400035）

0 引 言

在國內《信號與系統》著作中[1-2]，均介紹了R-H準則。文獻[1]中，基于無源有耗網絡阻抗函數的所有零點均位于s平面左半平面的事實，間接證明了R-H準則的正確性。本文在文獻[3-4]的基礎上，給出了一種導出R-H準則的方法。R-H準則遺留的問題：（1）在R-H陣列中，某一行的首元素為0時，如何完成R-H陣列的計算； （2）在R-H陣列中，某一行的元素全部為0的原因是什么，如何完成R-H陣列的計算，計算的結果對LTI連續時間系統的特征根分布是否存在影響。通過分析和討論，本文將解決R-H準則遺留的相關問題。

1 R-H準則的有關引理

設n次多項式D(s)為：

考慮到式（1），則有：

式（2）表明，D(-s)=0的根與D(s)=0的根在s平面上對虛軸互為鏡像關系。

為了分析問題方便，現作下述定義：

將D(s)=0的根均位于s平面左半平面的多項式D(s)，稱為霍爾維茨多項式，得到引理Ⅰ。

引理Ⅰ：D(s)為霍爾維茨多項式的充要條件是：

證明：首先證明充分性。若D(s)是霍爾維茨多項式，則式（4）成立。

考慮到式（1）和式（2），則式（3）可寫成：

式中：

若λi與λi+1是D(s)=0的一對共軛根，考慮到 式（6），則Wi(s)與Wi+1(s)之積可表示成：

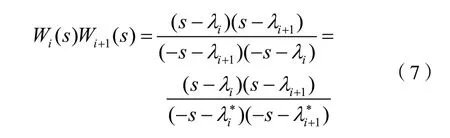
考慮到式（7），則Wi(s)可表示成：

設λi=αi+jβi，如 遇 實 根，則 取βi=0。考 慮 到s=σ+jω，由式（8）可得：

由于D(s)是霍爾維茨多項式，因此滿足αi=Re[λi]＜0(i=1,2,…,n)。于是，有：

考慮到（10），由式（5）可得：

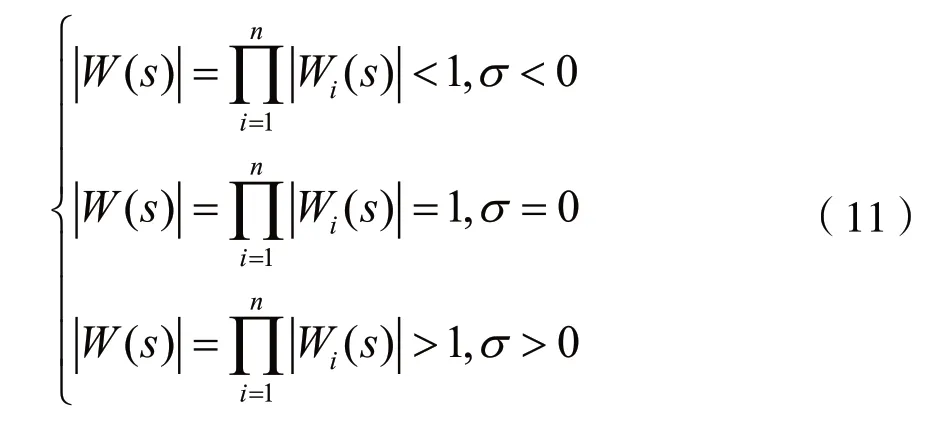
式（11）表明，若D(s)是霍爾維茨多項式，則式（4）成立。

再來證明必要性：若滿足式（4），則D(s)是霍爾維茨多項式。

采用反證法證明。設D(s)不是霍爾維茨多項式，那么D(s)=0在s平面的右半平面內有根。由式（2）可知，D(-s)=0在s平面的左半平面內有根。由式（3）可知，W(s)在s平面的左半平面（σ＜0）內必有極點，在極點的鄰域內，|W(s)|＞1，與式（4）相矛盾。

因此，式（4）是D(s)為霍爾維茨多項式的充要條件。

再定義：

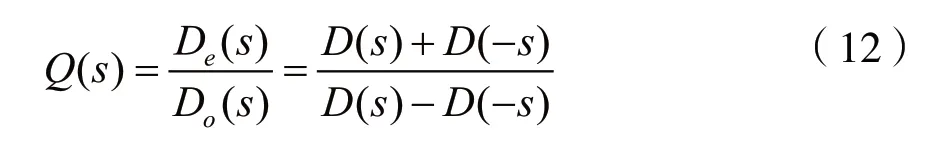
由于Q(s)是偶次項之和De(s)與奇次項之和Do(s)之比，因此Q(s)的分子和分母最高次冪相差1。當n為偶數時，s=0和s=∞分別為Q(s)的單零點和單極點；當n為奇數時，s=0和s=∞分別為Q(s)的單極點和單零點。令s=jω，不論n為偶數還是奇數，則Q(jω)都是ω的虛奇函數。

考慮到式（3），則（12）可表示為：

由式（13），得到引理Ⅱ。

引理Ⅱ：D(s)為霍爾維茨多項式的充要條件是：

證明：首先證明充分性。若D(s)是霍爾維茨多項式，則式（14）成立。

將W(s)用極坐標表示，即：

考慮到式（15），由式（13）可得：

考慮到式（4），由式（16）可知，若D(s)是霍爾維茨多項式，則式（14）成立。

再來證明必要性：若滿足式（14），則D(s)是霍爾維茨多項式。

采用反證法證明。設D(s)不是霍爾維茨多項式，那么D(s)=0在s平面的右半平面內有根。由式（2）可知，D(-s)=0在s平面的左半平面內有根。由式（3）可知，W(s)在s平面的左半平面（σ＜0）內必有極點，在極點的鄰域內，|W(s)|＞1，由式（16）可知Re[Q(s)]＞0，這與式（14）相矛盾。

因此，式（14）是D(s)為霍爾維茨多項式的充要條件。

引理Ⅲ：D(s)為霍爾維茨多項式的充要條件是Q(s)僅在s平面的jω軸上有單極點，且有實的正 留數。

證明：先來證明充分性。若D(s)是霍爾維茨多項式，則Q(s)僅在s平面的jω軸上有單極點，且有實的正留數。

設Q(s)在s=s0處有m階極點，則在s0的鄰域內，可用式（17）任意地逼近Q(s)，即：

式中，k＞0，θ為實數，m為正整數。

又設s-s0=ρejφ(0≤φ≤2π)，則有：

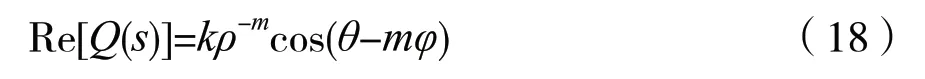
由式（18）可知，在以s0為圓心、ρ為半徑的圓周上，Re[Q(s)]的符號隨著mφ的變化而變化。若D(s)是霍爾維茨多項式，由式（14）可知，在s平面的左半平面內或右半平面內，Re[Q(s)]的符號是不改變的。因此，Q(s)的極點s0不能位于s平面的左半平面內或右半平面內，只能位于s平面jω 軸上。

Q(s)在jω軸上的極點s0是否允許為多重極點？這是需要解決的一個問題。考慮在以s0為圓心、ρ為半徑的圓周上，-π/2＜φ＜π/2與σ＞0等價，π/2＜φ＜3π/2與σ＜0等價，則式（14）可寫成：

在式（18）中，若m＞1，即取m是大于1的整數，則Re[Q(s)]在以s0為圓心、ρ為半徑的圓周上，將至少變四次符號，這與式（19）相違背。因此，在jω軸上不允許Q(s)有多重極點。如果m=1，滿足式（19）的θ的唯一允許值為：

由于s0是Q(s)在虛軸上的一階極點，則kejθ是它的留數，這就證明了若D(s)為霍爾維茨多項式，則Q(s)僅在s平面的jω軸上有單極點，且有實的正留數。

再來證明必要性：若Q(s)僅在s平面的jω軸上有實的正留數的單極點，則D(s)是霍爾維茨多 項式。

假設n為偶數，則式（12）可寫成：

考慮到s=σ+jω，由式（21）可得：

顯然，式（22）滿足式（14），也滿足式（4）。

這樣就證明了D(s)為霍爾維茨多項式的充要條件是Q(s)僅在s平面的jω軸上有實的正留數的單極點。

引理Ⅲ可作為檢驗的基礎，即列出Q(s)并確定其極點位置，這些極點必是jω軸上的單階極點，且留數為正實數，但仍需通過對Q(s)的分母進行因式分解才能確定jω軸上的這些單極點。

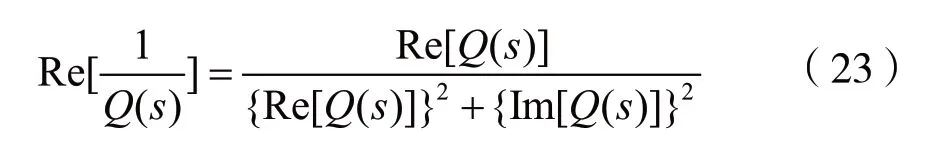
2 羅斯—霍爾維茨準則

2.1 霍爾維茨準則

設：

由式（24）可知，G(s)可以寫成：

若D(s)為霍爾維茨多項式，由引理Ⅲ可知，C1＞0，且G1(s)可寫成：

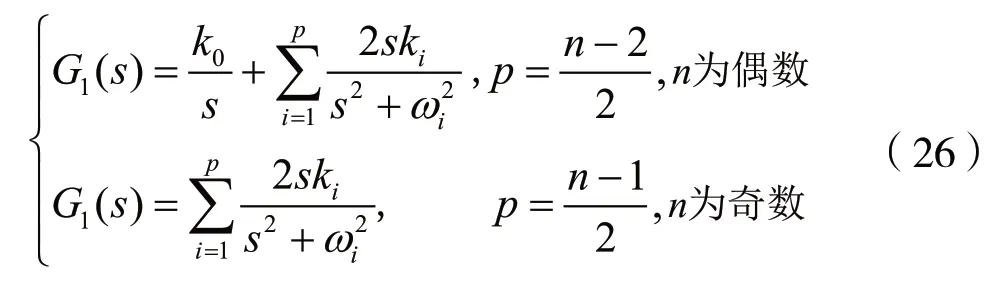
式中，k0＞0，ki＞0。

由式（24）和式（25）可知，若將G1(s)寫成兩個多項式之比，則分母多項式的次數只能比分子多項式的次數高一次，則1/G1(s)可寫成：

式（26）表明，G1(s)也僅在s平面的jω軸上有單極點，且留數為正實數。由引理Ⅲ可知，式（27）中的C2＞0，且要求G2(s)也僅在s平面的jω軸上有單極點，且留數為正實數。

同理，有：

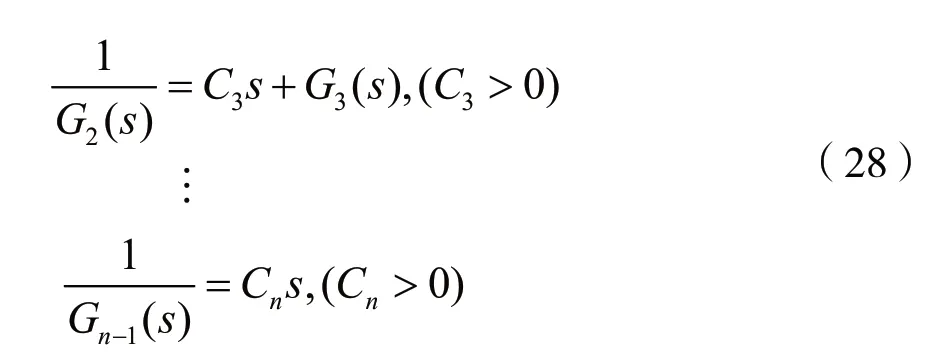
分析表明，若n階LTI連續時間系統是一個因果穩定系統，則保證n次多項式D(s)=0的根均位于s平面左半平面的充要條件是：D(s)的偶次多項式之和De(s)與奇次多項式之和Do(s)輾轉相除的商Ci(i=1,2,…,n)均為正值。反之，若D(s)=0的根均位于s平面的右半平面，則由引理Ⅰ和引理Ⅱ可知，式（18）中的θ、m只能分別取π和1。由引理Ⅲ和引理Ⅳ可知，Q(s)及1/Q(s)僅在s平面的jω軸上有單極點，且有實的負留數，也就是說，相應的n個Ci值均小于零。可見，Ci為正值、負值的個數與D(s)=0的根位于s平面左半平面、右半平面的數目相對應。

2.2 羅斯準則

考慮到式（24），有：

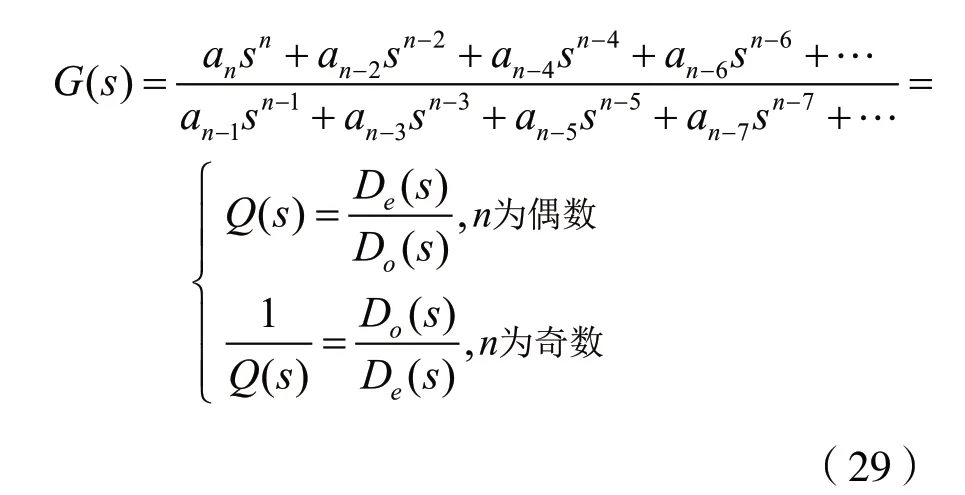
第一次長除，有：

顯然：

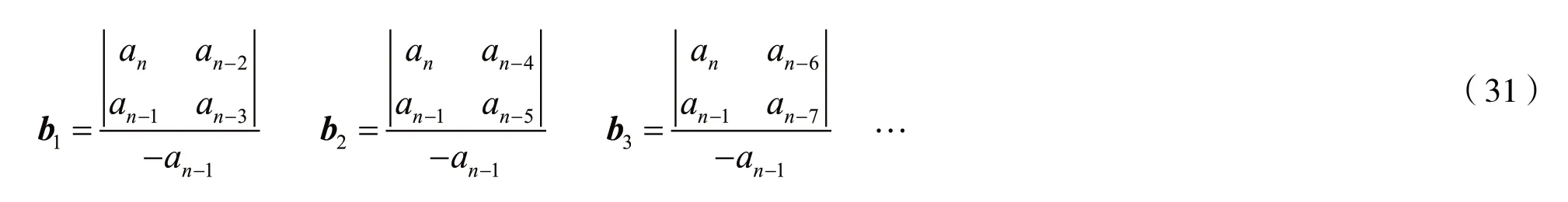
第二次長除（輾轉相除，用除數除以余數），有：

顯然：

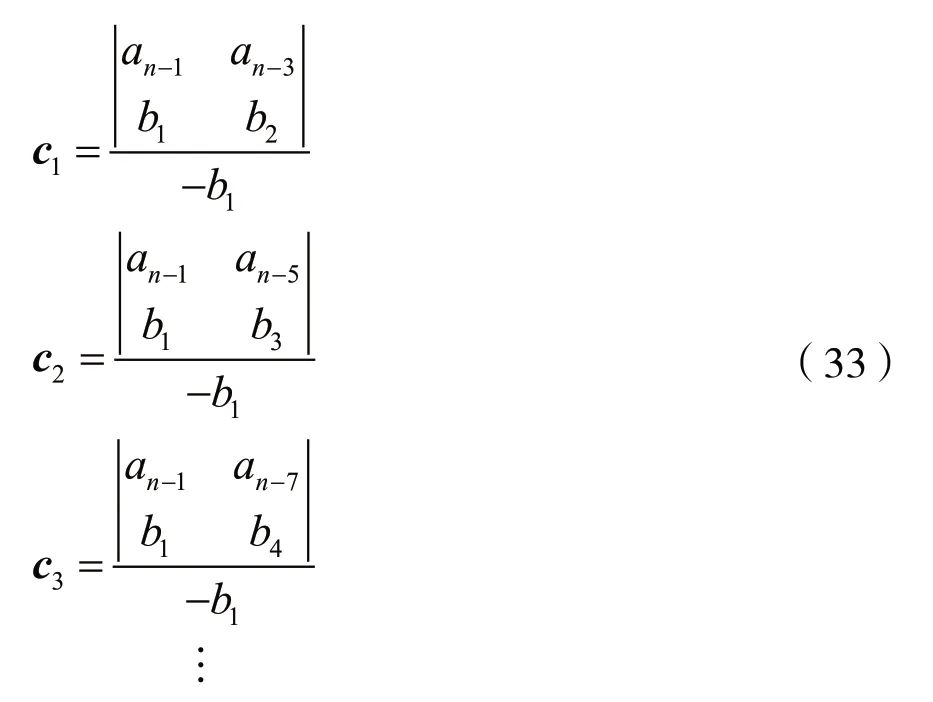
由此得到羅斯陣列或稱R-H陣列，即：

這個陣列的第一行和第二行是多項式D(s)各冪次的系數的交替排列，其余各行是通過輾轉相除運算后得到的。第一行除以第二行的商為C1s(C1=an/an-1)，所得的余部構成陣列的第三行，且第三行的列元素比前兩行的列元素少1；第二行除以第三行的商為C2s(C2=an-1/b1)，所得的余部構成陣列的第四行，且第四行的列元素又自動減1，直到構成n+1行為止，其中n個Ci值為R-H陣列中第1列的n+1個元素交替之比。可見，n個Ci值為正值的等效判據是R-H陣列中第1列的元素應具有相同的符號。同時，根據霍爾維茨準則的結論可知，若R-H陣列中的第1列的元素有正有負，則相鄰兩個元素符號改變的總次數正好是D(s)=0的根位于s平面右半平面的數目。

3 特殊情況的處理

3.1 R-H陣列中某行的第一個元素為零，而其余元素不全為零

R-H陣列中某行的第一個元素為零，其余元素不全為零，可用下述三種方法進行處理。

（1）將此行的第一個元素用無窮小量ε代替，并繼續排完整個R-H陣列。可以證明，第1列元素符號改變的總次數與ε（正與負）無關。

（2）將R-H陣列對應的多項式D(s)乘以因子(s+1)得到Dn+1(s)，展開Dn+1(s)再構成新的R-H陣列進行檢驗，可以避免出現上述情況。然而，Dn+1(s)=0與D(s)=0在s平面右半平面的根的個數相同。

（3）利用多項式D(s)構成一個相伴的倒數多項式D@(s)=snD(s-1)，對D@(s)用R-H陣列進行檢驗，可以避免出現上述情況。由復變函數的映射理論可知，D@(s)=0與D(s)=0在s平面右半平面的根的個數相同。

3.2 R-H陣列中出現全零行

這種情況發生在兩個相鄰行對應元素成比例時，實質是因為De(s)與Do(s)中有公因子A(s)所致。R-H陣列中，全零行的上一行就是這個公因子。若將多項式D(s)的最高冪次置于R-H陣列的第一行之前，并依次在下一行中降低冪次，則可將公因子A(s)找出來。由于A(s)是De(s)與Do(s)的公因子，而De(s)是全偶多項式，那么A(s)一定也是全偶多項式。因此，A(s)=0的根一定是關于原點對稱分布的，且A(s)=0的根是D(s)=0的根的一部分。因此，R-H陣列中出現全零行是D(s)=0有零實部共軛根的必要條件（但非充分條件）。為了確定D(s)=0在s平面右半平面的根的數目，相應地也有下述三種處理方法。

（1）可用偶次多項式A(s)的導數A′(s)的系數代替全零行來完成整個R-H陣列的計算。利用Rouché定理可以證明，多項式A(s)+A′(s)并沒有比多項式A(s)增加位于s平面右半平面根的數目。

（2）從R-H陣列中找出A(s)后，D(s)=A(s)DA(s)， 根據A(s)及A(s)之前的各行中的第一個元素，便可確定DA(s)=0的根的個數及其分布，而A(s)=0的根可用因式分解給出。

（3）從R-H陣列中找出A(s)后，對一些特殊的偶次多項式A(s)而言，可令A(s)中的重新構成多項式A0(p)，再用R-H陣列檢驗其根的分布，并注意A(s)=0的根關于原點對稱分布的特點，即可確定A(s)=0的根的分布。

例1：設：

試確定D(s)=0的根的分布情況。

s解：R-H陣列為：

于 是A(s)=2s6+4s4+4s2+2，D(s)=A(s)DA(s)，顯然：

即：

多項式DA(s)的R-H陣列如下：

可見，多項式DA(s)的R-H陣列中第1列的元素符號相同，故DA(s)=0的兩根均在s平面的左半平面。

分析表明，從多項式D(s)的R-H陣列中得到的C1和C2的值與從多項式DA(s)的R-H陣列中得到的C1A和C2A的值相同，因此可直接采用多項式D(s)構成的R-H陣列中得到的C1和C2的值來確定DA(s)=0的根的分布情況。

綜上所述，為了確定D(s)=0的根的分布情況，則確定A(s)=0的根的分布情況成為關鍵問題。解決A(s)=0的根的分布問題，通常有下述三種方法。

方法1：用A(s)的導數A′(s)的系數代替全零行，繼續完成整個R-H陣列的計算。

注意，由于R-H陣列中的運算是行列式運算，某行乘以或除以一個正數，僅影響下一行各元素的大小，而不影響各元素的符號。

由于R-H陣列中第1列元素的符號改變了兩次，故D(s)=A(s)DA(s)=0有兩個根位于s平面的右半平面。又因為DA(s)=0的兩個根均位于s平面的左半平面，故A(s)=0有兩個根位于s平面的右半平面。

則有：

因R-H陣列中第1列元素的符號相同，故A0(p)=0的根均位于p平面的左半平面。又因A0(p)是三次（奇次）多項式，故A0(p)=0一定有一個負實根，那么A(s)=0在s平面的jω軸上一定有一對共軛虛根。考慮到A(s)是六次多項式及A(s)=0的根是關于原點對稱分布的，那么A(s)=0在s平面的右半平面上一定有一對共軛復根。

方法3：通過對公因子偶次多項式A(s)進行因式分解來確定其根。

考慮到：

則有：

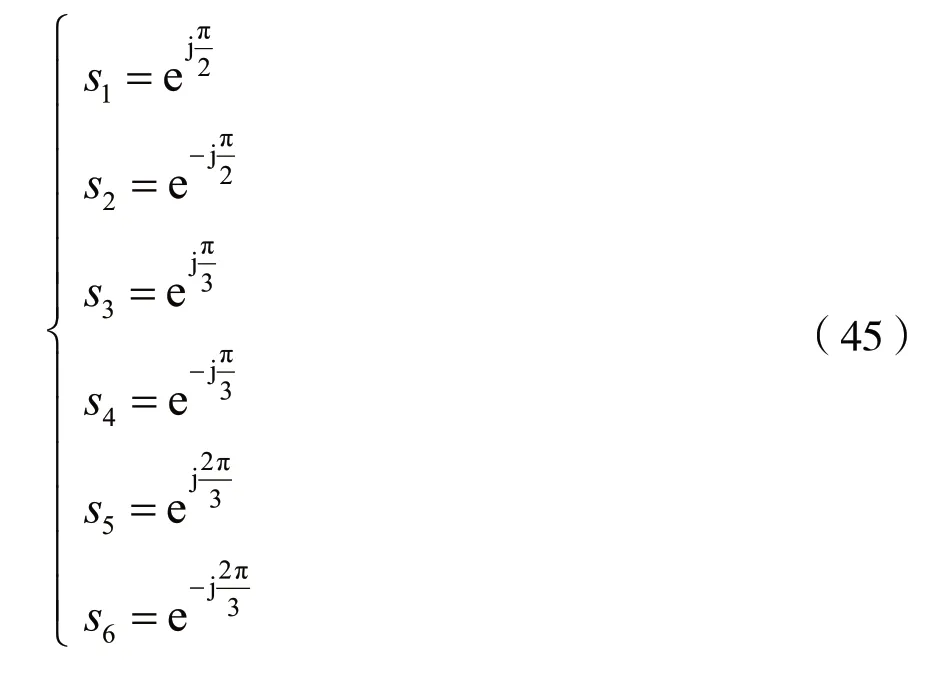
式（45）表明，A(s)=0的根在s平面上的分布不僅對稱于原點，而且有一對共軛根位于s平面的右半平面。

4 結 語

本文在文獻[3-4]的基礎上，基于映射和留數的概念，給出了一種導出R-H準則的方法。針對R-H陣列中某一行的首元素為0的情況，給出了三種處理方法；針對R-H陣列中某一行的元素全部為0的情況，不僅剖析了原因，而且給出了三種處理方法，成功解決了R-H準則的遺留問題。