一種LMS算法的實現及應用*

賴 川

（西南電子技術研究所，四川 成都 610036）

0 引 言

現代戰爭中，接收機不但會受到外部環境干擾信號的影響，同時也會受到自身發射機信號的影響，導致接收信號變差，無法正常接收信號，甚至導致通信中斷。消除這些噪聲的主要方法是使用濾波器濾波。濾波器可以較好的過濾干擾信號，保證正常信號到達接收端，從而改善通信狀態。但是，一般的濾波器需要根據頻點范圍的變化而變化，即需要濾波的范圍越大，濾波器就需要做的足夠寬，從而導致設備成倍增加；同時，濾波器的濾波范圍也有限，如果干擾信號頻點和接收信號頻點太近，濾波器基本就沒有效果了。有沒有一種濾波器能夠自適應的根據接收頻點調整信號，過濾非接收頻點的噪聲信號成為人們研究的重點。

自1960年Windrow和Hoff等人提出最小均方誤差（Least Mean Square，LMS）算法以來，人們在自適應濾波方面取得了豐碩的成果。LMS算法具有結構簡單，計算量小，穩定性好，易于實現等優點，在自適應濾波中得到的廣泛應用。但是，LMS采用了固定步長的收斂算法，導致前期干擾信號強時，收斂效果明顯；后期信號變弱，步長過大，導致收斂變慢的問題也十分突出。于是，人們提出來各種有效的方法來修正定步長帶來的收斂速度和穩態誤差的問題。文獻[1-2]提出了一種Sigmoid函數變步長LMS算法，較好的提高了迭代后期收斂速度問題。單是Sigmoid函數過于復雜。文獻[3]采用了類似Sigmoid函數的變步長算法，但是簡化了Sigmoid函數，增加了a，b兩個修改因子修改Sigmoid函數，較好的改進了Sigmoid函數算法在誤差接近零時，收斂較差的問題。但是a，b值選取不好的話效果會變得更差。文獻[4]針對該問題提出了a，b可變方法，更好的改進了Sigmoid函數提升了收斂速度和效果。文獻[5]提出了一種分段函數思想，在迭代初期，使用較大的步長，迭代后期使用較小的步長，依次解決收斂后期速度變慢的問題。文獻[6-7]還提出了其他一些變步長函數的方法，以此提高收斂速度和收斂效果。但是這些算法都沒有考慮真實信號對算法收斂性能的影響。

隨著理論的深入研究，人們逐漸將研究的中心從理論轉移到算法的實際硬件實現。文獻[8-13]都是講述了不同的變步長LMS算法如何在DSP（Digital Signal Process）上實現，并實際軟仿真測試了實現后的算法的噪聲抑制效果，均得到了較好的噪聲抑制和較快的收斂速度。隨著各種變步長算法在DSP上的實現及其取得的抑制效果，人們又逐步開始將基于DSP實現LMS算法應用到具有實際背景的環境中，來抑制具體的干擾噪聲：文獻[14-15]都是利用DSP芯片實現了不同的變步長LMS算法，并將它應用在聲回波系統中，有效的抑制了回波噪聲，提高了話音的音質。文獻[16]則利用DSP實現了一種變步長算法，用他來解決立體聲回波對接收端的噪聲影響，取得了很好的效果。這些研究僅僅是利用DSP芯片實現LMS算法，再模擬實際噪聲環境，進行干擾抑制，分析了這種架構的可行性，沒有進行實際的工程設計及驗證。文獻[17]提出了一種工程實現方案，但最后也僅僅是進行的軟仿真，得到了噪聲抑制的可行結論。

本文設計一種根據采集的實時信號決定迭代步長的算法，確保不同的信號采用不同的步長進行收斂迭代的方式，避免了單一變步長方式中，所有信號均采用一種變步長方式的方法。文章簡單分析了硬件設計思路，重點關注算法的設計和DSP的實現，并將實現的算法用于實際工程中進行對消測試，取得了較好的效果。

1 對消原理及算法分析

對消原理如圖1所示。原始輸入信號中除了有用信號S外，還混入了不相關的噪聲信號N0。要使系統輸出獲得高質量的有用信號S，就需要自適應濾波器通過調整接收到噪聲參考信號N1，產生一個與N0信號幅度相等，相位相差180度的信號Y（理想情況）疊加到原始輸入中，使得系統輸出干凈的有用信號S（實際為S+N0-Y）。

圖1 對消原理圖

假設S和N0、N1不相關，但是N0和N1是相關的，則有：

故當輸出E的期望值最小時，N0與Y的期望值也越小。此時，Y信號就是N0的最優期望值。為了實現這個目標，我們采用LMS算法。

基于最速下降法的固定步長LMS算法的迭代公式如下：

其中：X(t)=[x(t),x(t-1),…,x(t-M+1)]T為時刻t的參考通道輸入信號矢量；W(t)=[W0(t),W1(t),W2(t),…, WM-1(t)]T為T(t)時刻自適應濾波器的權系數；M為濾波器階數；d(t)為主通道輸入信號；e(t)為誤差；μ為收斂步長，控制穩定性和收斂速度。

如果迭代過程中，μ值始終保持不變，則表示該算法為定步長算法，如果μ在迭代中會變化，則表示算法為變步長算法。

2 硬件設計及算法實現

2.1 硬件設計

數學上，一個向量的表示可以用直角坐標系的兩個坐標表示，也可以采用極坐標系的幅度和相位兩個指標表示。對于一個信號矢量，如果我們想知道這個信號的具體情況：要么采集它的幅度和相位值；要么對其進行正交分解，得到X軸和Y軸的信號強度值。對于前者，我們采集幅度強度和相位值是比較困難的。因此，本文采用正交分解的思想，將輸入的信號進行分解，采集信號在X軸和Y軸的信號強度值。

圖2 矢量正交分解圖

進行信號分解后，自適應濾波器只需要根據采集到的X、Y兩路的干擾信號強度，修正濾波器輸出的X、Y兩路的信號強度，達到抑制干擾信號的目的。因此，濾波器階數為M=2。同時，硬件設計需要滿足對信號的正交分解及分解后的信號強度 檢測。

2.2 基于采樣的變步長算法

由于不同頻點的信號會有一定的差異，為了適應不同信號的抑制，本文在做射頻抑制前，先采集信號樣本，作為迭代步長的參考，具體方式如下：

設步長μ為如下表達式：

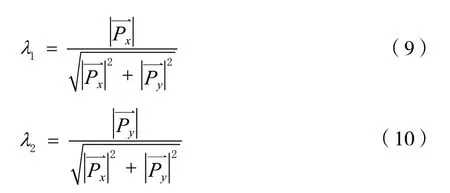
其中，a為常量收斂因子，λ為與采樣值有關的變量。由于采用了正交分解，因此本文的濾波器階數為2，設矢量信號的正交分解向量為采用歸一化處理，則有：

故得到：

2.3 DSP算法實現

算法的實現需要進行反復的迭代，以達到射頻抑制的效果，所以對運算的速度要求很高，而數字信號處理器就具有運算速度快、計算精度高、硬件配置強等特點，非常適合用于算法的開發和實現。我們采用TI公司生產的TMS320C6416芯片。該芯片具有最快1.39 ns指令周期時間，可以達到5760MIPS運算速度，具有兩路乘法器，每個時鐘周期支持最大4路16*16bit的乘法運算或者8路8*8 bit的乘法運算。同時，芯片自帶1M內部RAM，滿足程序內部取數要求，豐富的外圍接口，可以極大的減少外圍電路的開發。

整個算法實現分為4大塊：

（1）初始化。包含芯片配置初始化，全局變量初始化。

（2）采集零漂值（即沒有任何信號輸入時采集到的信號強度），作為收斂基準。

（3）采集信號樣本值。

（4）根據采集到的輸入信號值，進行迭代計算，直到某次采集結果值和零漂值的誤差在設定的閾 值內。

具體實現流程如下：

開始；

（1）芯片初始化，全局變量初始化，其中a=0.1，Th=10。a表示常量收斂因子，Th表示收斂門限。

（2）獲取當前狀態下設備內部零漂值sx,sy。sx表示x軸零漂信號值，sy表示y軸零漂信號值。

（3）采集樣本信號值x0,y0；進而得到λ1和λ2的值。

（4）采集對消后的信號強度值，如果|xnowsx|+|ynow-sy|≤Th.成立，則執行下一步，否則繼續執行當前步驟。

（5）迭代結束。

具體流程如圖3所示。

3 測試結果

采用圖4中所示測試環境進行測試，其中：信號源輸出18 dBm的信號，進過10 dB功分器分成兩路信號，一路信號直接輸入給對消設備的參考信號N1；另一路經過20 dB衰減后作為干擾信號N0和正常信號S進行合成后輸入到設備另一個輸入口。對消前后結果反映在頻譜分析儀上。選取了5個點進行測試，涵蓋了包括高中低三段頻點值。單載波測試結果見表1；FM信號（頻偏1 kHz，調制信號頻率400 Hz）測試結果見表2；AM信號（調制度 5%，調制信號頻率400 Hz）測試結果見表3，通過表格統計結果可以發現，基于DSP實現的LMS對消算法對三種波形均能實現了40 dBm以上的對消比；根據統計迭代次數及時間可以發現，整個迭代次數最大不超過160次，時間不大于20 ms。

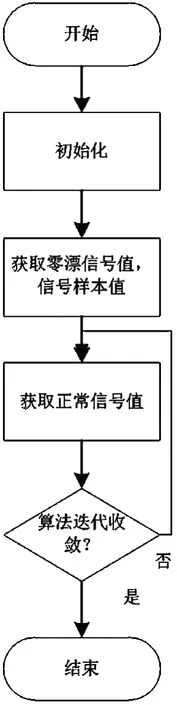
圖3 算法迭代流程

圖4 對消性能測試

表1 單載波測試結果

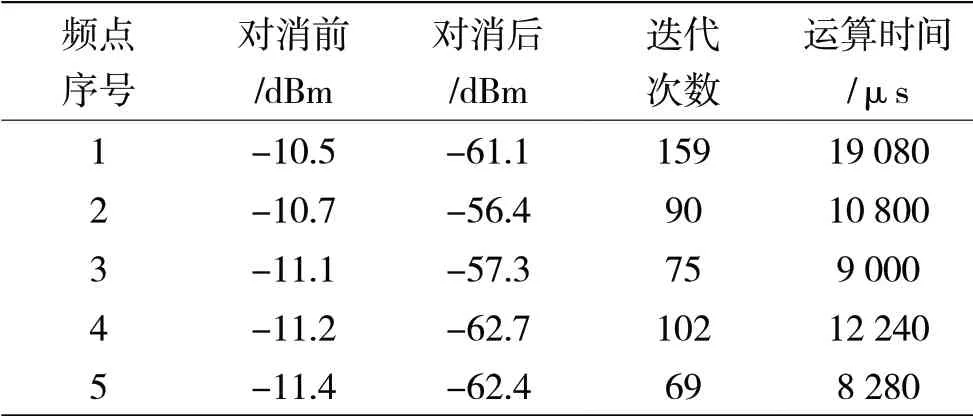
表2 2FM測試結果

表3 3AM測試結果

4 結 語

本文采用的基于采樣值決定當前頻點迭代步長方式的LMS算法，具有收斂速度快、抑制效果好的特點。實物測試結果表明：該變步長LMS算法不僅僅適用于單載波的噪聲抑制，也適用于FM、AM信號的噪聲抑制，具有很好的工程應用效果。下一步，將考慮實現實時變步長算法，進一步提高對消收斂的速度、進一步降低對消時間的消耗。