直方圖與餅形圖的保密生成協議*
葛 雪,王穎囡,竇家維
陜西師范大學數學與信息科學學院,西安 710119
1 引言
網絡的迅速發展為多個參與者利用各自的保密數據聯合進行數據挖掘、知識發現、信息搜索以及尋求數據之間的各種統計規律、合作進行科學研究等提供了巨大的機會,同時也給參與者的信息安全帶來了巨大的挑戰.在互不信任的網絡環境中,參與者需要保護各自所擁有數據的隱私,在聯合計算過程中稍有不慎就可能導致數據的機密性喪失與隱私泄露.運用安全多方計算技術,既能充分發揮機密數據的作用,又能保護數據的機密性與隱私,這使得安全多方計算越來越受到人們的關注.
1982年姚期智[1]提出了兩個參與者的安全計算問題,1988年Ben 和Goldwasser[2]引入了多個參與者的安全多方計算問題.安全多方計算是指兩個或更多參與者利用各自的保密數據,聯合進行的保密計算.計算結束后,沒有參與方能夠獲得多于規定輸出的信息.安全多方計算是網絡空間信息安全與隱私保護的關鍵技術,它對于計算科學、密碼學和信息安全的理論與實踐都有重要的意義,是國際密碼學界近年來的研究熱點[3–5].Goldwasser[6]預言具有豐富理論基礎和廣泛應用前景的安全多方計算將成為計算科學一個必不可少的工具.Cramer[7]也指出安全多方計算將成為計算科學一個威力強大的工具.
Yao、Goldwasser 以及Goldreich 等人[8–10]奠定了安全多方計算的理論基礎.他們證明了所有安全多方計算問題都是可解的,并給出了解決方案.但是他們指出這些解決方案存在的共同問題是它們的效率都太低了,利用這些通用的解決方案去解決現實生活中各種各樣的問題是不切實際的.因此對具體問題應該設計具體的解決方案.
在Goldwasser,Goldreich 和Cramer 關于安全多方計算研究與論述的激勵下,人們研究了各種各樣的安全多方計算問題,如保密的科學計算[1,11–17]、保密的計算幾何[18–20]、保密的統計分析[21,22]、保密的數據挖掘[23–25]、其他安全多方計算的應用[26,27]等,但仍有許多問題需要研究.
其中,保密的統計分析是研究如何在合作環境下進行統計分析,并確保每個參與者自身數據的安全性,這在自然科學、工程技術、社會科學的各個方面都有非常廣泛的應用.本文主要研究了保密生成直方圖、餅形圖的問題,這是保密的統計分析中一個非常重要的問題.就目前我們所知,還沒有見到關于這個問題的解決方案.直方圖與餅形圖是一種統計報告圖,二者的優點是可以直觀地看出數據整體的分布情況.與數據的排序相比,直方圖與餅形圖更加直觀,在數據較多時,對數據進行一一進行排序是不太現實的,會耗費過多的人力物力而收益甚微.在實際生活中,直方圖、餅形圖有非常多的應用場景,比如:一個學校想要知道學生成績的分布情況,但是每個班的成績、每個同學的成績都屬于個人隱私,同學們不想對外公布,這時候就涉及到保密求直方圖、餅形圖的問題.另外,對于各地區隱私疾病直方圖、保密投票數據的直方圖與餅形圖等等在現實生活中都十分常見,因此研究直方圖與餅形圖的保密生成問題是十分必要的.
本文的主要貢獻如下:
(1)提供了一種新的編碼方法,能夠將參與者的保密數據隱藏在數組中.
(2)利用該編碼方法結合Paillier 加法同態加密算法,設計了第一種保密生成直方圖的解決方案.該方案可以抵抗P1不參與時的合謀攻擊.
(3)利用該編碼方法結合橢圓曲線加法同態加密算法以及門限加密算法,設計了第二種保密生成直方圖的解決方案.第二種方案可以抵抗任意數量的合謀攻擊,并且效率也提高許多.
2 預備知識
2.1 安全性定義
半誠實模型:所謂半誠實參與者[10]是指那些在協議的執行過程中按照協議要求忠實地履行協議的參與者,但他們可能會記錄下協議執行過程中收集到的所有信息,在協議執行后試圖根據記錄的信息推算出其他參與者的輸入.如果所有的參與者均為半誠實參與者,這樣的計算模型稱為半誠實模型.由于半誠實參與者不對協議實施主動攻擊,所以半誠實模型又稱為誠實但好奇(honest-but-curious)模型或被動模型.
設有n個參與者P1,···,Pn,分別具有保密數據x1,···,xn,記X=(x1,···,xn).他們利用協議Π保密地計算f(X)=(f1(X),···,fn(X)),其中fi(X)(i∈[n]={1,···,n})為參與者Pi得到的輸出結果.在協議執行過程中,Pi得到的信息序列記為
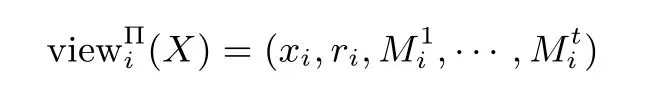
其中,ri表示Pi在協議中產生的隨機數,(j=1,···,t)表示Pi收到的第j個信息.對于部分參與者構成的子集I={Pi1,···,Pis}?{P1,···,Pn},記
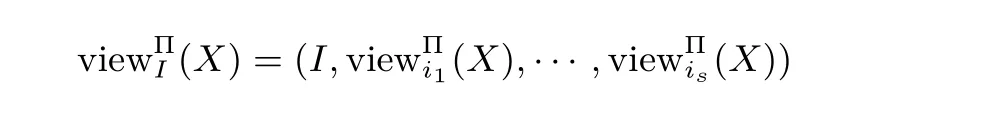
定義1(半誠實參與者的安全性[10])在參與者都是半誠實的情況下,如果存在概率多項式時間算法S,使得對于任意的I={Pi1,···,Pis}?{P1,···,Pn},均有下式成立:
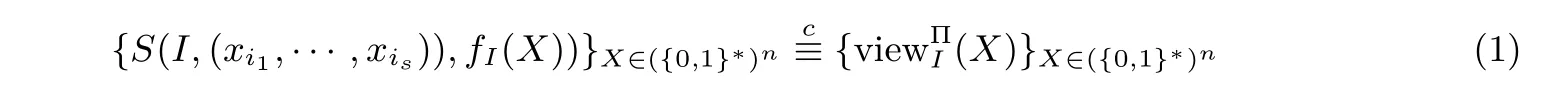
其中表示計算上不可區分,則稱協議Π 保密地計算了n元函數f(X).
顯然,如果對于任意n?1 個參與者構成的集合Γ,都存在滿足(1)式的S,則協議Π 能夠抵抗任意的合謀攻擊.
2.2 Paillier同態加密算法
同態加密的概念在文獻[28]中被首次提出,它可以保證在不影響明文數據機密性的情況下,直接操作密文來完成對明文的計算.簡單來說,對密文的計算等價于明文計算之后再加密.
Paillier 方案[29]的具體過程如下.
密鑰生成給定一個安全參數k,選擇兩個素數p,q,使得|p| =|q| =k,其中N=p×q,λ=lcm(p?1,q?1)是p?1 和q?1 的最小公倍數.隨機選擇一個g∈,使得gcd(L(gλmodN2),N)=1,定義為L(x)=.算法的公鑰為(g,N),私鑰為λ.
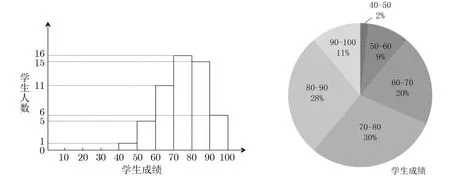
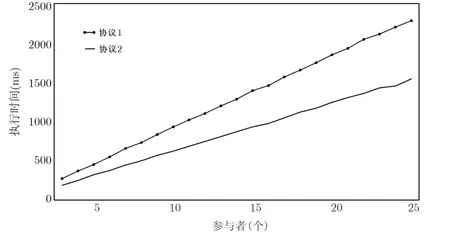
加密隨機選擇一個隨機數r,r 解密計算 該算法是概率加密算法,具有加法同態性.假設密文為 那么 因此該算法滿足如下性質: 橢圓曲線密碼體制ECC(elliptic curve cryptography)是1985年由Miller 和Koblitz 共同提出的.其理論基礎是定義在有限域上的某一橢圓曲線上的整數點與無窮遠點可構成有限交換群.如果該群的階包含一個較大的素因子,則其上的離散對數問題是困難的.與RSA 算法相比,ECC 具有計算量小、密鑰短、對帶寬和處理器要求低等優點.基于橢圓曲線實現ElGamal 密碼體制[30]描述如下. 在使用橢圓曲線密碼體制之前,必須設計把信息編碼到橢圓曲線上的點的編碼方法,具體如下[31]. (1)選擇一個具有n個點的橢圓曲線. (2)選擇一個輔助基本參數k,比如設k=20(加密解密雙方達成一致). (3)對于每一個m,Fori=1 tok?1,令x=mk+i,利用橢圓曲線方程求y.如果找到就停止,如果找不到就令i←i+1,繼續找,直到找到為止.實際上,可以找到一點(x,y),這個點就是消息m的編碼. (4)解碼:點(x,y)解碼為的值向下取整). 密鑰生成選定一條橢圓曲線EC(a,b)與其上的一個基點G,在上任意選擇一個隨機數h,計算H=hG.(H,G)就是公鑰,h是私鑰. 加密消息編碼到EC(a,b)上一點M,并產生一個隨機整數r,計算密文 解密對密文1,C2,用私鑰h解密得到明文為 該算法是概率加密算法,具有加法同態性.假設密文 那么 因此該算法滿足如下性質: 門限解密[32,33]是安全多方計算中對抗合謀攻擊的一個重要工具.在門限解密密碼體系中,n個參與者共同生成一個公鑰,每個人持有一部分解密密鑰.在加密過程中可以直接使用共同擁有的公鑰加密消息,但是需要多個參與者共同合作才能對密文進行解密.如果解密一個消息至少需要t個人合作才能解密,少于t個人合作時將不能得到解密消息,這種密碼體制被稱為(t,n)門限密碼體制. 本文需要抵抗盡可能多的合謀攻擊,所以需要的是(n,n)門限密碼系統用于抵抗n?1 個參與者的合謀攻擊,這里可以利用橢圓曲線密碼系統構造門限密碼系統,具體構造如下. 密鑰生成選定一條橢圓曲線EC(a,b)與其上的一個基點G,每個參與者Pi在上任意選擇一個私鑰hi,計算Hi=hiG,共同生成公鑰 加密消息編碼到EC(a,b)上一點M,并在上任意選擇一個隨機數r:1rn?1,計算密文C1,C2=m+rH,rG. 解密對密文C1,C2,通過下面解密過程得到明文: 問題描述:假設現有n個參與者Pi(i=1,2,···,n),每一個Pi都有多個數據記為ei={ei1,ei2,···},他們希望合作計算這些數據的直方圖,同時不泄露其他任何私有信息(即參與方最后僅知道這些數據所生成的直方圖與餅形圖,并不知道其它參與者擁有的具體數據). 編碼方法:首先每一個參與者Pi共同商定將區間分割為m份,記為 {[y1,y2),[y2,y3),···,[ym,ym+1]} ={S1,S2,···,Sm},其中Si=[yi,yi+1)(i=1,2,···,m?1),Sm=[ym,ym+1],接著按照下面的方法構造數組: 其中對于i∈{1,2,···,n},k∈{1,2,···,m}, 以此方式,每個參與者的數據ei與數組Xi一一對應.對此得到的n個數組X1,X2,···,Xn求和,即將這些數組對應元素相加,得到一個新的數組: 數組T即為所求對應區間所含元素的個數.根據區間{[y1,y2),[y2,y3),···,[ym,ym+1]} 以及數組T可繪制出相應直方圖,對數組T稍加運算,計算出每個區間Si(i=1,2,···,n)所含元素個數占總數量的百分比,就可繪制出該數據的餅形圖.下面以某個年級學生的數學成績為例. 例1若將學生成績分為[0,10),[10,20),···,[90,100]這10 個區間段,繪制表1. 表1 某個年級學生的數學成績Table 1 Math scores of a grade 按照上述編碼方式, 計算向量對應分量之和即為 則可得出對應的直方圖,再稍加運算,可得到餅形圖(如圖1). 圖1 某個年級學生數學成績直方圖與餅形圖Figure 1 Histogram and pie charts of math scores of a grade 以上的編碼方法就是本文計算直方圖與餅形圖的基本原理.直接這樣計算是無法保密的,而在密文的條件下進行這樣的操作就可以實現保密運算.本文用Paillier 加密算法與橢圓曲線門限加密對數組中的0和1 進行加密,使得任何參與者都無法分辨出數組中0 與1 的個數(由于求出直方圖便可求出相應的餅形圖,為敘述簡潔,以下協議均僅求出直方圖). 首先,應用具有加法同態性質的Paillier 加密算法給出一種保密生成直方圖的基本方案,如協議1. 協議1直方圖的保密生成協議. 輸入Pi各自擁有的保密數據ei. 輸出該組數據的直方圖. (1)P1應用Paillier 公鑰系統生成私鑰sk 和公鑰pk,并公布公鑰pk. (2)每個參與者Pi(i=1,2,···,n)以公式(2)將自己的數據轉化成數組Xi=(xi1,xi2,···,xim). (3)每個參與者Pi(i=1,2,···,n)用公鑰pk 加密數組Xi得到E(Xi)=(E(xi1),E(xi2),···,E(xim)). (4)參與者Pi(i=1,2,···,n)計算如下(此處的向量相乘為E(Xi)和E(Xi+1)中對應分量相乘): (5)參與者Pn將E(Xn)發送給P1,P1計算X=Dec(E(Xn)),繪制相應的直方圖并公布. 正確性分析在協議1 中,由于Paillier 加密算法的加法同態性(即對密文做乘法運算等于對相應的明文做加法運算后再加密),可得出: 安全性分析由于只有P1有私鑰可以解密,所以協議可以抵抗沒有P1參加的任何合謀攻擊,但該協議不能抵抗有P1參與時的合謀攻擊.以下是關于協議1 安全性的具體分析. 定理1直方圖的保密生成協議在半誠實模型下是安全的. 證明:通過構造滿足式(1)的模擬器S來證明本定理,此處選用可能參與合謀的最大合謀結構進行模擬.分為以下三種情況: (1)P1不參與合謀,P2,···,Pn合謀能獲得P1的保密數據的信息. 因為只有P1才能夠解密密文,如果他不參與合謀,除了P2,···,Pn的數據和他們生成的密文之外,P2,···,Pn收到的關于e1的信息只有E(X1)=(E(x11),E(x12),···,E(x1m))=(c11,c12,···,c1m).由于加密算法是語義安全的,(ci1,ci2,···,cim)和m個隨機數是計算不可區分的.在此情況下, 給定輸入(I,(e1,···,en),fI(X)),S隨機選擇使得f(X′)=fI(,···,en)=(···,)=fI(X)=f(e1,···,en)=(t1,t2,···,tm)用···,en進行模擬.首先按照協議要求構造數組=(,,···,),加密得到 模擬器S 按照協議要求進行加密運算.解密最終數組E(X′)得到 令S(I,(e1,···,en),fI(X))={I,e2,E(X2),···,en,E(Xn),fI(X′)},因為概率加密方案是語義安全的,所以E(X1)(),且fI(X1)c≡fI(),其他所有參數都是相等的,故 因此對于e1是安全的. (2)P1不參與合謀,P2,···,Pn的n?2 個合謀想得到其中一個的保密數據,因為這時P2,···,Pn的地位是平等的,能力是相同的,不失一般性假設P3,···,Pn合謀要獲得P2的保密數據的信息.這種情況與第一種情況相同,用類似的模擬可以證明對于e2是安全的. (3)P1參與合謀.這種情況下的最大合謀結構仍然是包含P1的n?1 個參與者合謀,要得到某一個Pi∈{P2,···,Pn} 的某個參與者的保密數據ei所在的區間范圍,無法知道ei的大小. 綜上所述,該協議對于半誠實參與者是安全的. 在本文協議1 中,參與者Pi將E(Xi)先發送給Pi+1,Pi+1計算E(Xi)×E(Xi+1),并將其發送給下一個參與者,以此類推,直到Pn將最后的每個參與者加密向量對應分量的乘積E(Xn)發送給P1.P1將E(Xn)解密并公布,如果P1參與合謀攻擊,比如,參與者P1和P3合謀,會恢復出P2的數據.所以需要借助門限橢圓曲線加密系統設計一個更安全、更高效的協議,以達到抵抗合謀攻擊的目的.基本原理與上述相同,不再贅述. 協議2基于門限密碼系統的直方圖的保密生成方案. 輸入Pi各自擁有的保密數據ei. 輸出該組數據的直方圖. (1)n個參與者P1,···,Pn首先選定一條橢圓曲線EC(a,b),G為其上基點.每個參與者分別選擇一個私鑰hi,計算Hi=hiG,共同生成公鑰 將公鑰H公開,私鑰hi各自保留. (2)每個參與者P1,···,Pn分別做如下運算: (a)Pi將自己擁有的數據ei按公式(2)編碼方式轉化成數組Xi=(xi1,xi2,···,xim). (b)參與者Pi將數組Xi編碼到EC(a,b)上作為橢圓曲線上的點Mi=(Mi1,Mi2,···,Mim). (c)Pi在上任意選擇一個隨機數rij:1rijn?1,計算密文 并公布. (3)參與者P1,···,Pn將加密后的數據E(Mi)依次相加(即對應分量相加),并記 (4)參與者Pi計算hiC2j(j=1,2,···,m),并公布.P1,···,Pn將其依次相加將得到 (5)最后參與者Pi只需計算 并繪制相應的直方圖即可. 正確性分析在協議2 中,由于橢圓曲線密碼體制具有加法同態性質(即對密文做加法運算等于對相應的明文做加法運算后再加密),可得出: 所以協議2 是正確的,可以求出數組T,并繪制相應的直方圖. 安全性分析協議的安全性是基于橢圓曲線加密體制的安全性.由于門限橢圓曲線的公鑰是由所有參與者共同產生的,即其中hi是參與者Pi所持有的私鑰碎片,如果想解密的話,就必須擁有全部參與者的私鑰碎片.所以整個解密的過程都必須要全部參與者參與,因而可以抵抗合謀攻擊. 在計算過程中,每個參與者Pi對外僅公布了加密信息E(Mi),在解密過程中對外也僅公布了加密信息hiC2j(j=1,2,···,m),由橢圓曲線密碼體制的安全性可知,在協議解密過程中如果Pi沒有參與,將無法解密得到Mj.因此在解密過程中,Pi的數據是完全保密的.我們給出下面的定理,僅給出證明思路,詳細的證明過程省略. 定理2在半誠實模型下,基于門限密碼系統的直方圖的保密生成協議2 是安全的. 證明:證明協議的安全性需要構造滿足式(1)的模擬器S.根據語義安全的同態加密算法的性質,如果沒有私鑰,應用概率公鑰系統加密的任何信息都是計算不可區分的,因此只要有一個參與者不合謀,對其他合謀者來說,他們實際執行協議時獲得的view 和用滿足生成直方圖不變的任意一組輸入進行模擬所得到的信息序列是計算不可區分的,所以只要在(1)式中令S(I,(xi1,···,xis)),fI(X))為模擬過程中的view,即可使(1)式滿足. 本部分對上述兩個保密生成直方圖的協議效率進行分析比較.本文方案都是用同態加密算法解決直方圖問題,基本運算都是模乘運算.(忽略各協議中所需要的乘法運算)用Paillier 加密系統加密或者解密一次需要進行兩次模指數運算.應用橢圓曲線加密系統進行的是模加運算,模加運算的次數與加密過程中所選隨機數r的二進制位數有關. 在本文協議1 中,每個參與者都需要對編碼后的數組元素進行加密,n個參與者需要進行2mn次模指數運算,所以協議1 在加密過程中需要進行2mn次模指數運算.最后P1對E(Xn)進行解密,需要2m次模指數運算.所以協議1 共需要2m(n+1)次模指數運算,計算復雜性為2m(n+1). 在本文協議2 中,參與者都需要對編碼后的數組元素進行加密,所以協議2 共加密2nm次.參與者利用自己的私鑰對密文聯合解密,共解密n次.加密和解密過程均需要進行模加運算,所以協議2 的計算復雜性是O(nlogr)模加運算(r表示加密過程中的隨機數且0rp?1). 衡量通信復雜度的指標一般用協議交換信息的比特數,或者用通信輪數.在安全多方計算研究中通常用輪數. 在協議1 中,每個參與者需要將加密后的密文發送給Pn,Pn將收到的密文做運算后發送給P1解密,在這個過程中需要n輪通信.最后P1解密,并且將解密結果告訴Pi,需要n?1 輪通信.所以協議1 共需要2n?1 輪通信,通信復雜性為O(n). 在協議2 中,所有參與者構造公鑰需要n?1 輪通信,加密過程宣布Mi,需要1 輪通信,解密過程宣布需要1 次通信,所以協議2 共需要n+1 輪通信,通信復雜性為O(n). 表2 協議性能比較Table 2 Protocol performance comparison 本節我們通過模擬實驗來測試執行協議1、協議2 所用的時間,通過協議執行的時間來驗證方案的效率執行情況. 實驗測試環境:Windows 10 64 位操作系統,Intel(R)Core(TM)i5-6600 處理器CPU @3.30 GHz,8.00 GB 內存,用java 語言在MyEclipse 上運行實現.本文所做模擬實驗均在此環境下進行. 實驗方法:本實驗中,我們的底層協議(Paillier 算法,橢圓曲線加密算法)是使用了現成的開源包.實驗設定m=10,參與者數分別為n=3,4,···,25.為使數據準確,對n的每個設定值進行1000 次模擬實驗測試,統計協議執行時間的平均值(忽略協議中的預處理時間).圖2 描述了協議的執行時間隨參與者個數增長的變化規律. 圖2 協議的執行時間隨參與者個數增長的變化規律Figure 2 Execution time of agreement varies with growth of number of participants 由圖2 可知協議的執行時間隨參與者個數增長而線性增加,并且很容易得出,基于橢圓門限解密的保密直方圖生成方案效率要高于基于Paillier 加密算法的保密直方圖生成方案. 本文設計了一種新的編碼方法,以新的編碼方法與同態加密算法為基礎,分別利用Paillier 加法同態加密算法、門限橢圓曲線加法同態加密算法構造了保密生成直方圖問題的兩個安全多方計算協議.第一個協議在半誠實模型下是安全的,但不能有效地抵抗合謀攻擊.第二個協議可以抵抗多達n?1 個參與者的合謀攻擊.將協議加以推廣可以適用于更加普遍的情形,今后將在現有的研究基礎上進一步研究抗惡意參與者(主動攻擊者)的直方圖問題.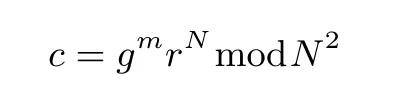
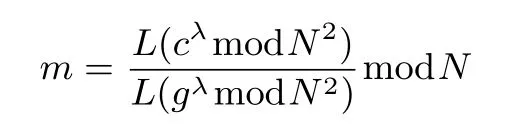
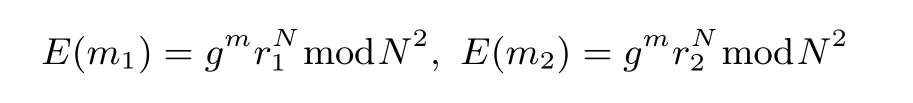
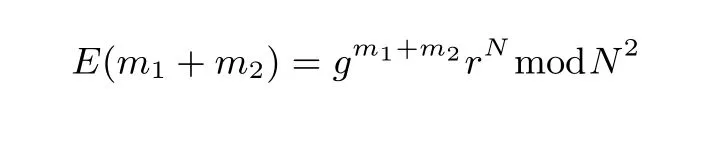
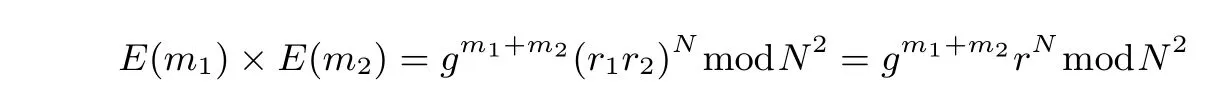
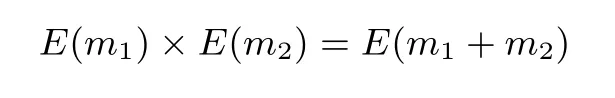
2.3 橢圓曲線同態加密算法
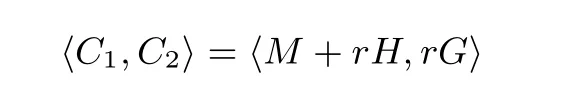
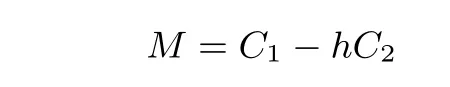
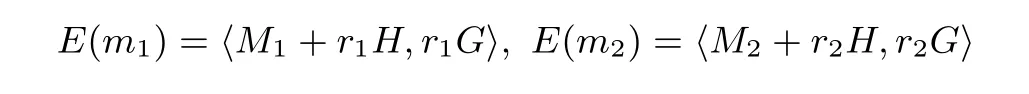

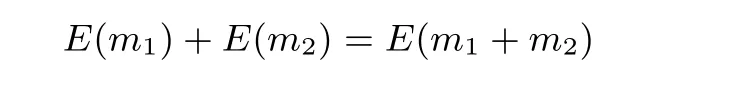
2.4 門限解密
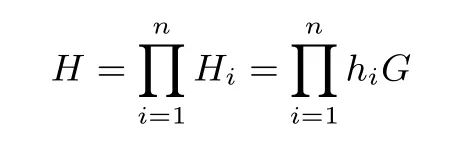
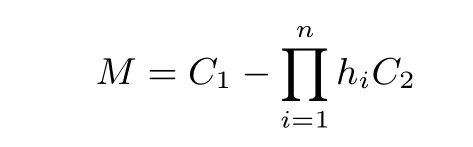
3 直方圖保密生成協議
3.1 協議的基本原理

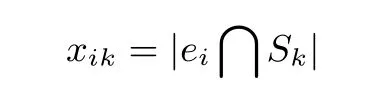
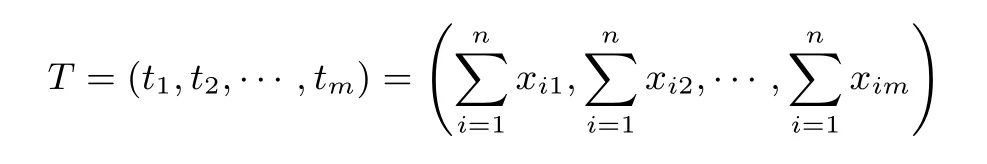


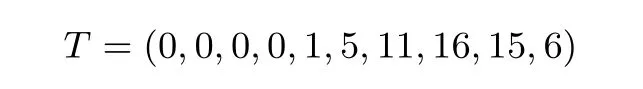
3.2 基本的直方圖保密計算方案
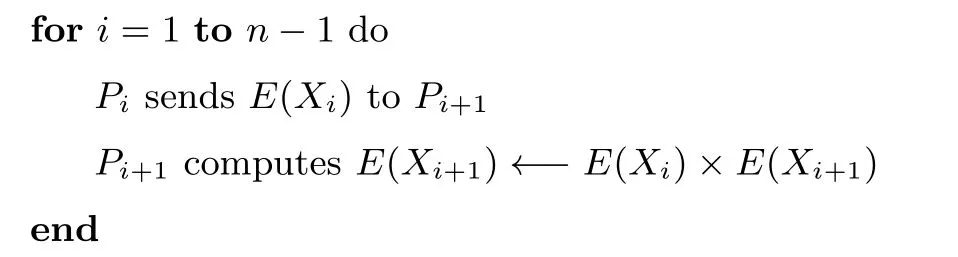
3.3 方案分析
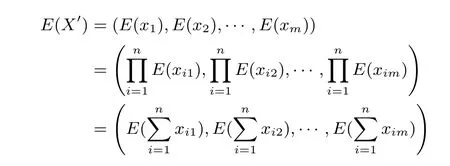
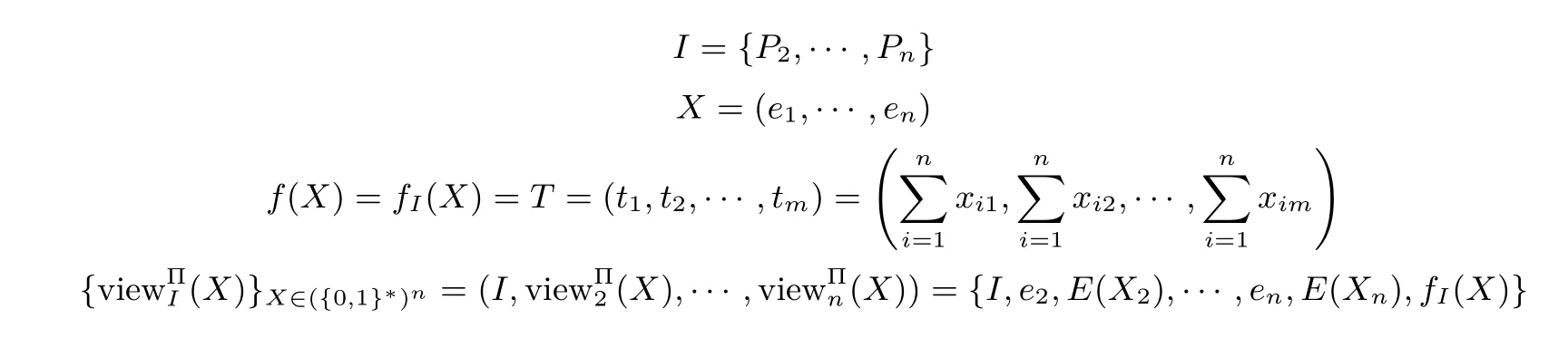
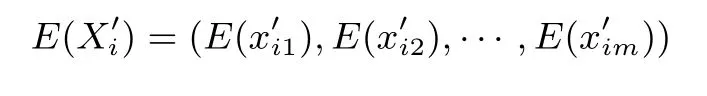
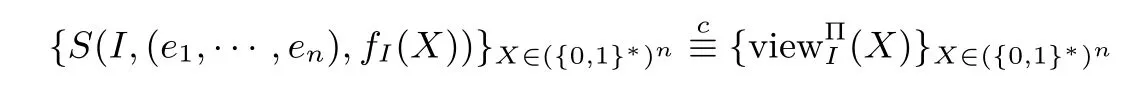
4 基于門限解密的直方圖保密生成協議
4.1 基本原理與協議
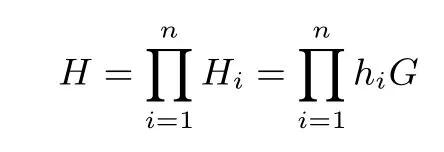
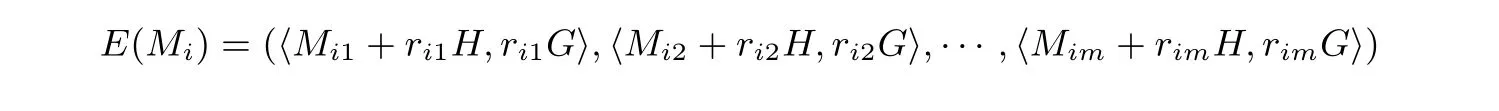
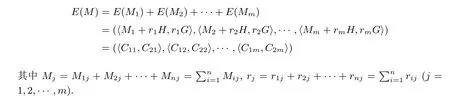
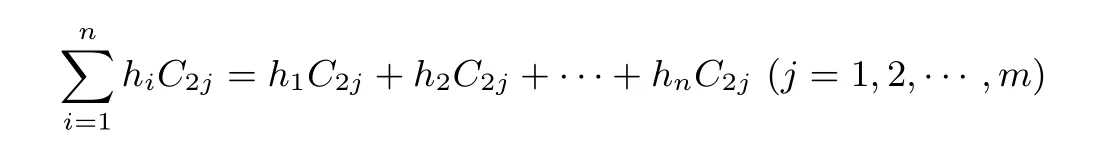
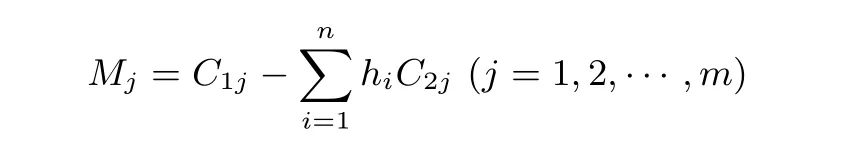
4.2 方案分析
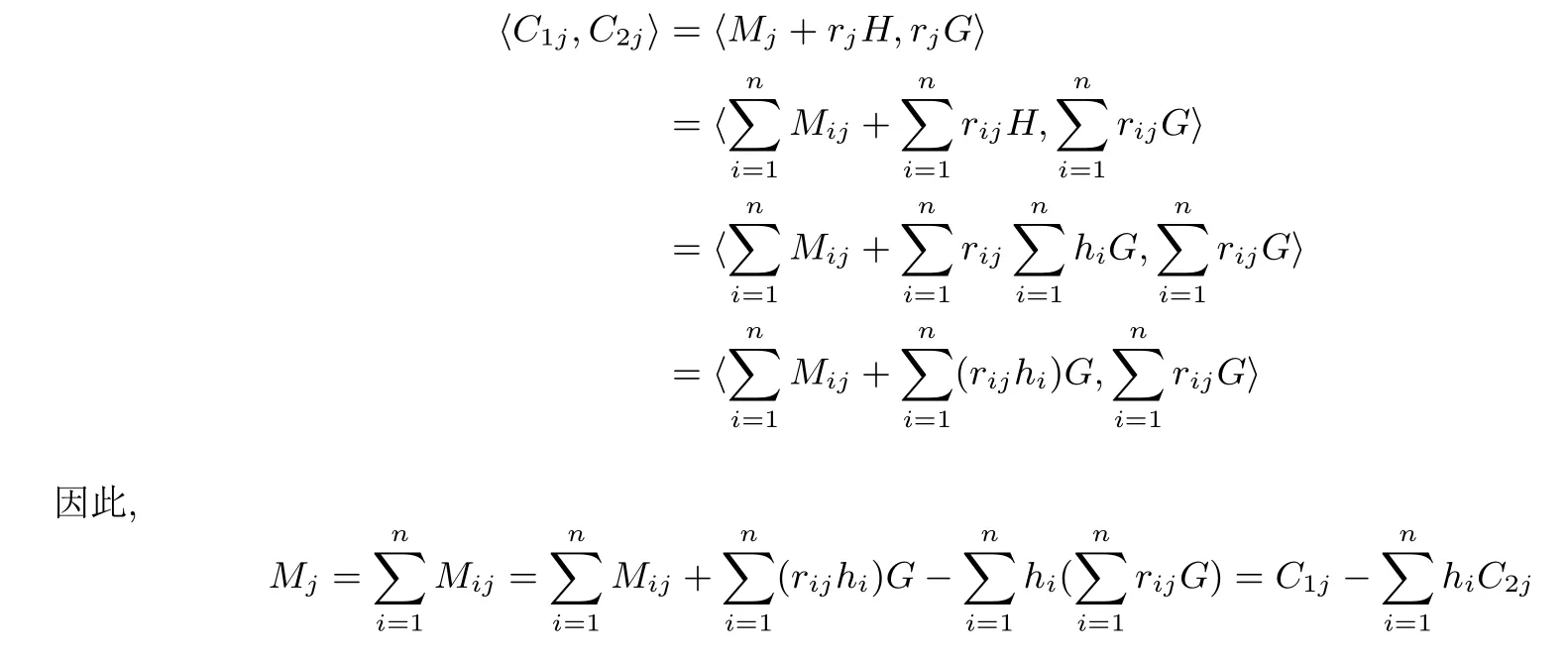
5 協議的效率分析
5.1 計算復雜性
5.2 通信復雜性

5.3 實驗數據分析
6 結論

