矩陣與增廣矩陣秩相等問題的保密計算及應用*
杜潤萌,劉旭紅,李順東,魏 瓊
1.陜西師范大學 計算機科學學院,西安 710119
2.陜西師范大學 數學與信息科學學院,西安 710119
1 引言
矩陣是現代科技領域必不可少的工具,在自然科學、工程和社會科學的各個領域都有著重要的應用價值,矩陣是圖像處理、線性規劃、各種網絡研究的關鍵工具和手段.矩陣的秩是反映矩陣固有特性的一個重要參數[1],用矩陣方法解決問題的核心手段是利用矩陣的秩,所以科學計算中的許多與矩陣相關的問題都可以歸約到矩陣秩的計算,許多保密的科學計算問題也都可用矩陣秩的保密計算協議解決.因此,矩陣秩的保密計算是安全多方計算的一個基本問題,有著重要的意義.
安全多方計算(secure multiparty computation,SMC)是指在不泄露自己隱私數據的情況下,多個參與者利用他們的私有數據進行合作計算,計算結束后沒有參與方能獲得多于規定輸出的信息,是近年來國際密碼學界的研究熱點[2].SMC 最初是由姚期智教授提出來的,Goldreich 等人[3,4]對安全多方計算的理論進行了深入研究,證明了在一定的條件下,任意函數f(x1,···,xn)的安全多方計算都是可以實現的,并且給出了基于不經意傳輸的解決方案.這樣的通用解決方案有重要的理論意義,奠定了安全多方計算的理論基礎,但是用通用解決方案解決實際的安全多方計算問題是不合理的,對具體的問題應該研究具體的解決方案.同時Goldreich 利用比特承諾[5]和零知識證明[6]設計了一個編譯器,借助這個編譯器,可以自動生成一個對于半誠實參與者和惡意參與者都安全的多方計算協議,該協議可以強迫惡意參與者以半誠實的方式參與協議的執行過程,否則將被發現.
安全多方計算的研究在計算科學中占有重要的地位和廣泛的應用前景,這激勵著人們研究各種具體的安全多方計算問題[7].所研究的問題可以總結為以下幾類:保密的科學計算問題[8];保密的統計分析問題[9];保密的數據挖掘問題[10];其他安全多方計算問題.關于科學計算的兩方安全計算問題,美國普渡大學的Du 博士在其論文中還指出了科學計算其他值得研究的問題[11]:矩陣特征值、特征向量、行列式、矩陣因子分解等.Cramer 和Damg?rd 在線性秘密共享下首次研究了線性代數中各種各樣的安全計算問題:如矩陣的行列式、矩陣的秩、線性方程組、特征多項式等問題,并給出了解決方案[12].
文獻[13]給出了一個判定加密矩陣的奇異性的協議.基于此協議,解決了計算加密矩陣的秩和線性方程組解的問題.但該文利用矩陣的奇異性去判斷矩陣的秩,要求矩陣必須為n×n的方陣,因而解決方案不具有普遍意義.此外,方案采用同態加密體制,計算復雜性較高.在國內,線性代數問題同樣得到了廣泛深入的研究.文獻[14]將Du 的工作推廣到多方的情形.方案需要多次調用兩矩陣乘積協議以及不經意傳輸協議,計算復雜性與通信復雜性都很高.文獻[15]提出的保密計算矩陣秩的協議,需要Alice 和Bob 兩個人合作計算一個m×n矩陣的秩,但計算復雜性是O(mn2).文獻[16]基于安全點積協議設計了個多方向量組秩的協議.但求矩陣秩的時候需要調用mn次點積協議,計算復雜性是O(m2n),其中m表示參與者個數,n表示每個參與者所擁向量的維數,這個方案的計算復雜性也較高.
綜上所述,現有的關于矩陣秩的保密計算協議存在幾個方面的不足:解決方案的適用性有限;基于公鑰加密算法設計的方案計算復雜性較高;用矩陣的秩解決的實際問題有限.針對這些問題,本文假設Alice擁有一個矩陣Am×n,Bob 擁有一個矩陣Bm×1,設計了一個安全高效的計算增廣矩陣(A|B)秩的協議.將矩陣秩的計算推廣到一般的矩陣,提出了不需要加密運算的高效保密計算協議,并以此判斷矩陣與增廣矩陣秩是否相等.判斷矩陣與增廣矩陣秩是否相等的保密計算可以作為一個基本建筑模塊,用于構建許多安全多方計算問題的協議,包括保密判定空間直線與直線(平面與直線、平面與平面)的位置關系、保密判斷多項式整除、保密判斷集合包含問題和任意數整除問題、保密判斷線性方程組解的數目等應用,拓寬了矩陣秩的保密計算的應用領域.
空間兩直線位置關系問題的多方保密計算方案在實際應用場景中具有重要的研究意義.例如:航空公司A 和航空公司B 在同樣的兩個國家之間分別設計了一條航線圖L1和L2,他們想在不泄露自己航線圖的情況下保密地判定L1和L2是否相交,確保航線的安全性.所以他們需要合作計算兩條空間航線是否相交.現實中很多問題都可以歸約到空間位置關系的保密判定,因此研究這個問題有著重要的應用價值.由于平面和直線在直角坐標系下可分別用三元線性方程和三元線性方程組來表示,而線性方程組解的數目和系數矩陣關系密切,因此可用保密判定矩陣與其增廣矩陣的秩是否相等的方法來判斷空間直線與直線(平面與直線、平面與平面)的位置關系.
本文研究矩陣與增廣矩陣秩的相等問題的保密計算,主要貢獻如下:
(1)研究了矩陣與增廣矩陣的秩是否相等的安全多方計算問題,提出了一種新的、不需要加密運算的、適用于一般矩陣的高效解決方案,為解決其他多方保密計算問題提供一種新的方法.
(2)在保密判斷矩陣和增廣矩陣秩是否相等協議的基礎上,提出了保密判斷空間兩條直線位置關系的協議,方案安全且高效.
(3)在保密判斷矩陣和增廣矩陣秩是否相等協議的基礎上,提出了保密判斷兩個多項式是否可以整除的協議,也為解決其他多方保密計算問題提供一種新的途徑.
本文第2 節介紹了協議相關預備知識;第3–5 節設計了三種協議;第6 節分析了方案的效率;第7 節給出了文章的總結.
2 預備知識
2.1 安全性定義
半誠實參與者[17]本文方案的安全性均假設安全多方計算的參與者為半誠實參與者.半誠實參與者是指參與者在協議執行過程中將完全按照協議忠實地執行協議,但他們也會保留計算的中間結果試圖推導出其他參與者的輸入.
隱私的模擬范例[18]如果對于任意一個半誠實的參與者,在執行協議的過程中,參與者所獲得信息都可以通過他自己的輸入和輸出進行模擬,而且得到的消息序列與實際過程得到的消息序列不可區分,就說明協議是安全的.如果一個多方計算協議能夠進行這樣的模擬,即說明所有參與者都不可能從協議的執行過程中得到其他參與者任何有價值的信息.這就是研究安全多方計算問題時普遍接受的模擬范例.
一些記號假設雙方計算的參與者分別是Alice 和Bob.
(1)設f=(f1,f2)是一個概率多項式時間函數,π表示計算f的雙方計算協議.
(2)當輸入為(x,y)時,Alice(Bob)在執行協議π的過程中所得到的信息序列記為其中r1(r2)表示Alice(Bob)選擇的隨機數;表示Alice(Bob)第i次收到的信息.
(3)輸入為(x,y)時,執行協議π以后,Alice(Bob)的輸出結果記為
定義1(半誠實參與者的保密性)對于一個函數f,如果存在概率多項式時間算法S1與S2(也稱這樣的多項式時間算法為模擬器)使得
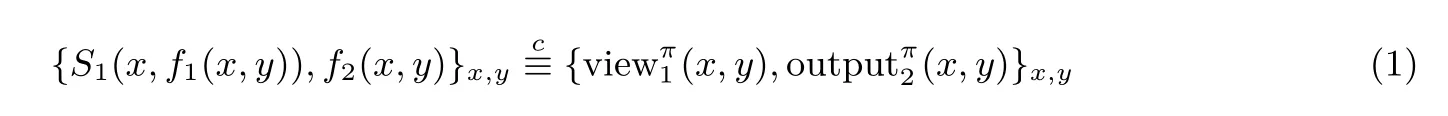
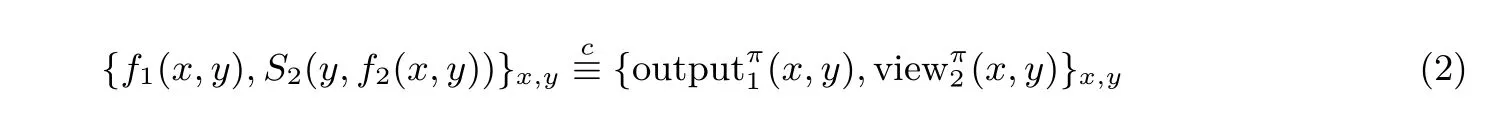
其中表示計算上不可區分,則認為π保密地計算f.
2.2 矩陣相關知識
矩陣的秩在m×n矩陣A中任取k行、k列(1kmin{m,n}),位于這k行、k列交叉點處的元素按原來次序組成的k階行列式稱為A的一個k階子式.矩陣A中不等于零的子式的最高階數稱為A的秩,記為R(A).
初等行變換設A為m×n矩陣,可對A實施以下三類初等行變換,將A化為行階梯矩陣或最簡行階梯矩陣.
(1)第一類初等行變換:將A的第i行與第j行交換位置;
(2)第二類初等行變換:將A的第i行乘以非零常數λ;
(3)第三類初等行變換:將A的第i行的λ倍加到第j行.初等變換不會改變矩陣的秩.
初等矩陣[19]由單位矩陣E經過一次初等變換得到的矩陣稱為初等矩陣.
從初等矩陣的定義可以看出,初等矩陣是方陣,并且每次進行初等變換都會有一個與之相對應的初等矩陣.共有三類初等矩陣,如圖1 所示.
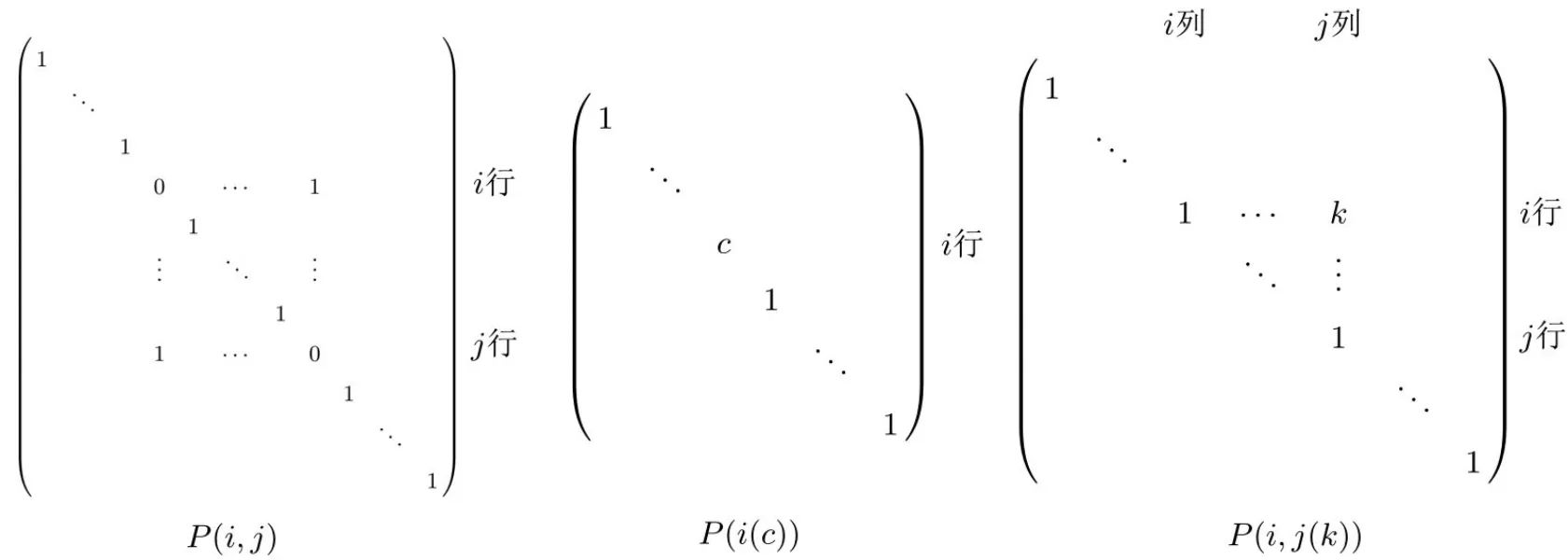
圖1 三類初等矩陣Figure 1 3 kinds of primary matrix
其中,P(i,j)表示互換矩陣E的第i行與第j行,P(i(c))表示用數域中非零數c乘E的第i行,P(i,j(k))表示把矩陣E的第j行的k倍加到第i行.由于本文中全部用的初等行變換,所以與列變換相應的初等矩陣不做討論.
用初等變換化矩陣為行階梯矩陣任意矩陣Am×n經過有限步的初等行變換,可將矩陣化為行階梯矩陣A′,特點是:可畫出一條階梯線,線的下方全為0,階梯線的豎線后面的第一個元素為非零元.例如矩陣
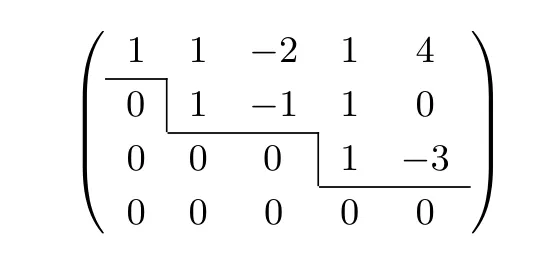
即為一個行階梯矩陣.因此存在初等矩陣P1,P2,···,Ps,使得下式
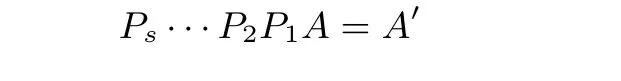
成立,記P=Ps···P2P1.
2.3 多項式整除與矩陣秩的關系
命題1有兩個多項式f(x)=anxn+an?1xn?1+···+a0x0,q(x)=cmxm+cm?1xm?1+···+c0x0,令g(x)=f(x)q(x).利用f(x)的系數并且每一列擴展m個0 構造矩陣A(m+n+1)×(m+1),利用g(x)的系數構造矩陣B(m+n+1)×1.f(x)整除g(x)的充分必要條件是其對應的系數矩陣滿足R(A)=R(A|B).
證明:必要性:g(x)=f(x)q(x)=a0c0x0+(a1c0+a0c1)x1+···+(asc0+as?1c1+···+a1cs?1+a0cs)xs+···+(am+nc0+am+n?1c1+···+a0cm+n)xm+n
從上式可以得出
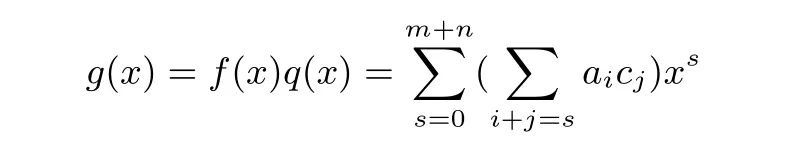
其中in,jm.
利用f(x)的系數并且每一列擴展m個0 構造矩陣A(m+n+1)×(m+1),利用q(x)的系數構造矩陣C(m+1)×1.令A與C作相乘的運算,可以得到矩陣B,如圖2 所示.
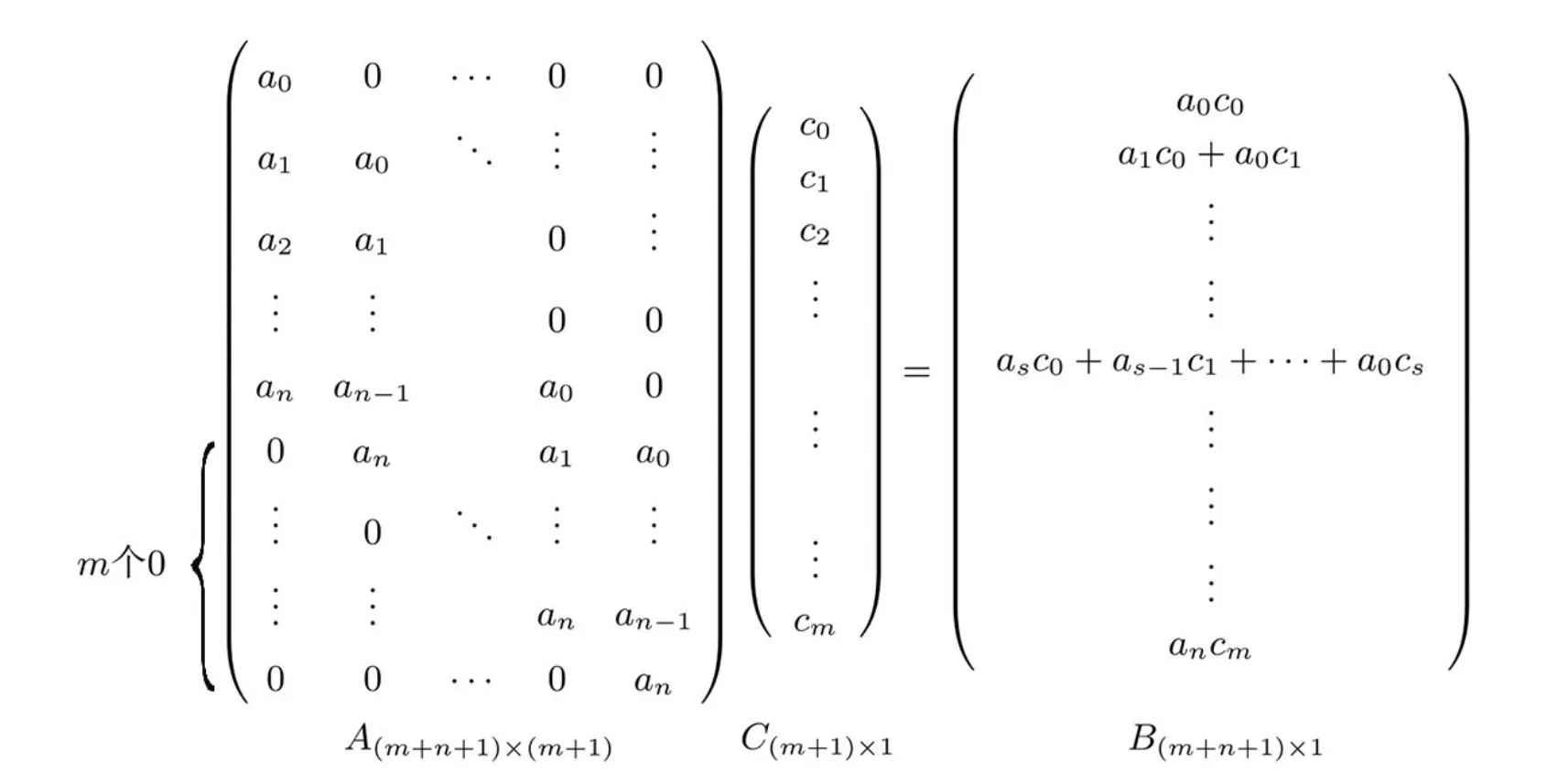
圖2 AC =BFigure 2 AC =B
從圖2 中比較A,B,C中的元素可以得出:
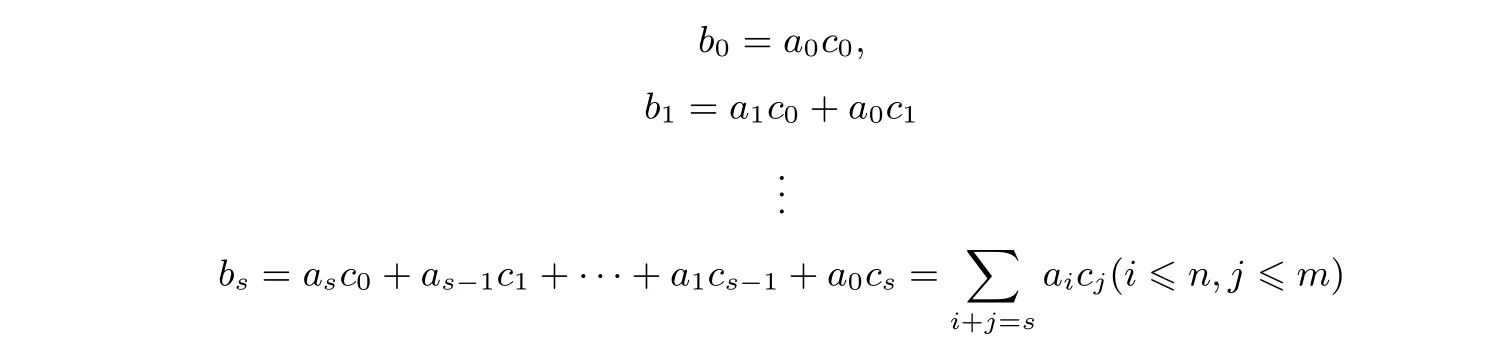
因此f(x)q(x)=g(x)等價于AC=B.f(x)整除g(x),而且有唯一的商q(x),等價于AC=B對應的線性方程組有解,而線性方程組有解的條件是矩陣A與增廣矩陣(A|B)同秩,也就是R(A)=R(A|B).同理可證充分性.
綜上所述,f(x)整除g(x)的充分必要條件是其對應的系數矩陣滿足R(A)=R(A|B).
3 矩陣與增廣矩陣秩相等問題
3.1 問題描述
Alice 有一個矩陣Am×n,Bob 有一個矩陣Bm×1,利用A,B構造增廣矩陣(A|B),其中
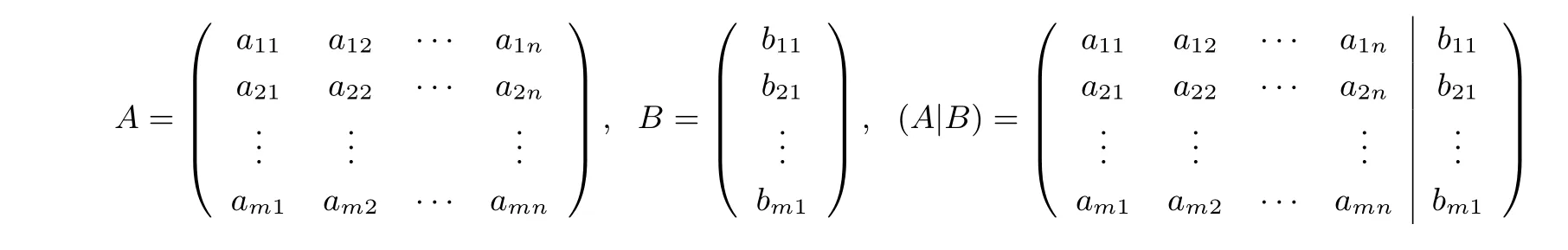
Alice 和Bob 都想在不暴露自己私有數據的情況下,判斷矩陣A和增廣矩陣(A|B)的秩是否相等.
協議的基本原理Alice 計算初等變換矩陣Pm×m發送給Bob,其中矩陣A′=PA.Bob 收到P后,計算PB得到矩陣B′發送給Alice.Alice 判斷矩陣A的秩與增廣矩陣(A|B)的秩是否相等.為方便表達,定義如下謂詞:
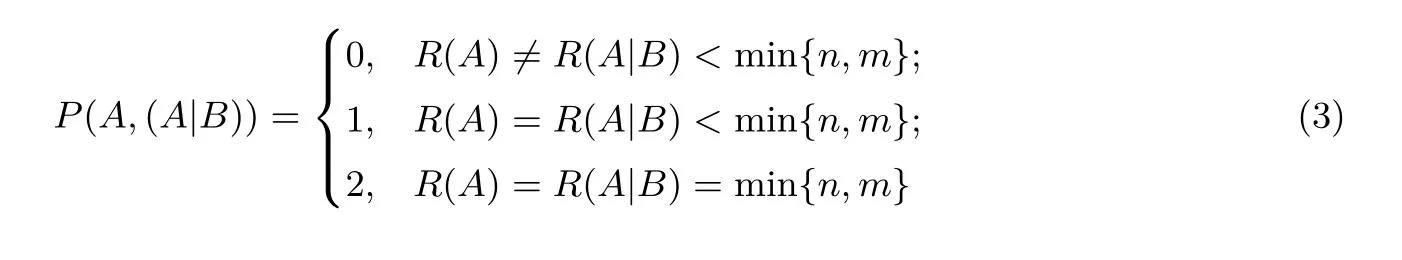
例如,Alice 有一個矩陣A3×3,Bob 有一個矩陣B3×1,Alice 計算出初等變換矩陣P3×3發送給Bob,其中
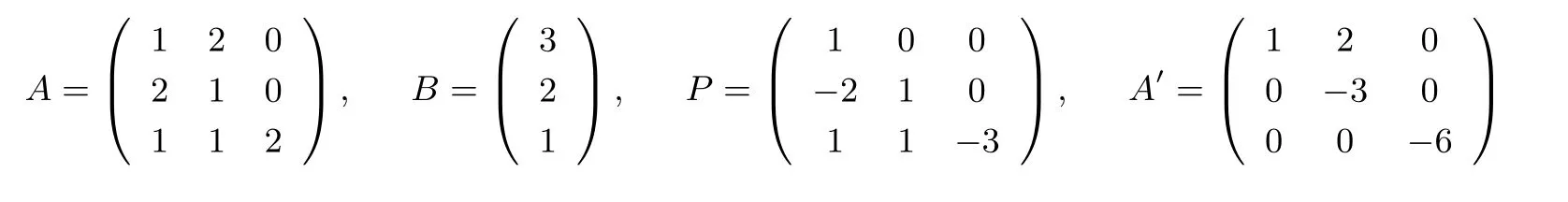
Bob 收到P后,計算PB得到矩陣B′,其中
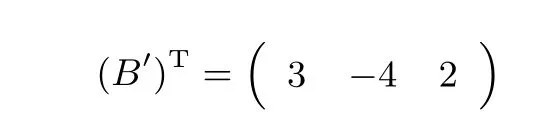
Bob 將矩陣B′發送給Alice.Alice 比較矩陣A′與增廣矩陣(A′|B′)秩的大小,其中
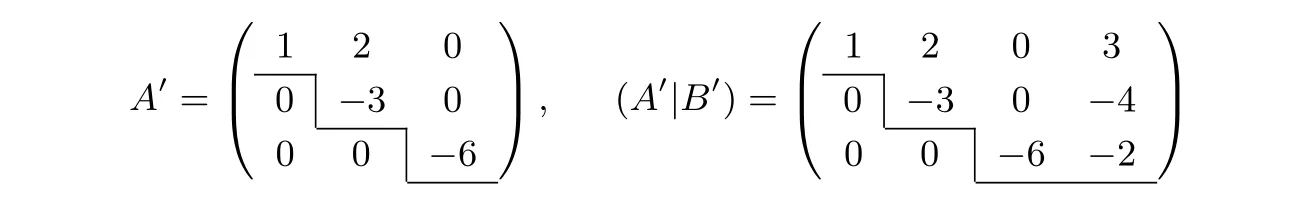
由此可知,R(A′)=R(A′|B′)=3,輸出P(A,(A|B))=2.上述原理是我們計算矩陣與增廣矩陣秩是否相等的基本思路,不涉及任何保密問題,保密計算矩陣秩的具體協議參看協議1.
3.2 矩陣與增廣矩陣秩相等問題保密計算方案
協議1保密的計算矩陣與增廣矩陣秩相等問題.
輸入:Alice 有一個矩陣Am×n,Bob 有一個矩陣Bm×1.
輸出:P(A,(A|B)).
(1)Alice 計算初等變換矩陣Pm×m.Alice 對矩陣P隨機化處理得到矩陣P′,其中

其中,ri是Alice 選取的有理數隨機數.Alice 將P′發送給Bob.
(2)Bob 計算P′B得到矩陣B′,其中
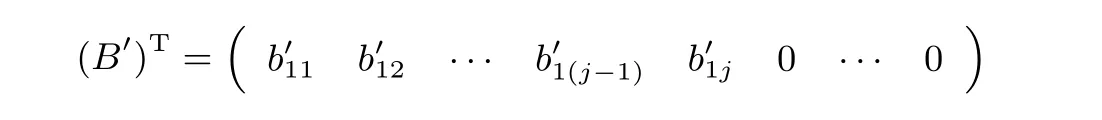
Bob 統計從以上緊挨并連續等于的個數和從開始以下0 的個數,分別記為p,q.Bob 將p,q發送給Alice.
(3)Alice 根據p,q進行判斷.若R(A)=R(A|B) 定理1在半誠實模型下,協議1 是正確的. 證明:(1)Alice 計算初等變換矩陣P和P′=P(r1,...,rm),其正確性是由對矩陣進行初等行變換不會改變的矩陣的秩保證的. (2)Bob 計算B′=P′B,這樣就可以保證Bob 與Alice 做的是同樣的初等變換. (3)Bob 統計從以上緊挨并連續等于的個數和從開始以下0 的個數,分別記為p,q.Bob將p,q發送給Alice.根據矩陣的秩的定義,Alice 根據p,q進行判斷即可得到增廣矩陣(A|B)的秩. 因此,協議1 是正確的. 協議1 的安全性分析為了分析協議1 的安全性,需要詳細分析在協議執行后可能推斷出的潛在信息. 首先考慮Alice 矩陣的安全性.Alice 對矩陣進行隨機化處理,Bob 在整個協議的執行過程中僅得到Alice 發送給他的矩陣P′.由于P′原本不是最簡矩陣,并且有r1,r2,···,rm為Alice 的保密數據,均可隨機選取(也可選擇有理數),即使Bob 有無限的計算能力,也無法推出矩陣P,更無法推出矩陣A. 同樣的,Alice 只知道p,q,所以Alice 也無法推斷出矩陣B. 定理2在半誠實模型下,協議1 是安全的. 證明:我們通過構造使得(1)和(2)成立的模擬器S1和S2來證明本定理,首先構造S1. (1)S1接受輸入(A,P(A,(A|B))),根據P(A,(A|B))的值構造矩陣B′,用A,B′進行模擬. (2)S1計算矩陣A的初等變換矩陣P,按照協議1 對P進行隨機化處理得到矩陣P′. (3)S1計算P′B′得到矩陣B′′.S1統計從以上緊挨并連續等于的個數和從開始以下0的個數,分別記為p′,q′. (4)S1比較R(A|B′)和R(A|B)是否相等. 在本協議中view1(A,B)={A,P,R(B),P(A,(A|B))}.令S1(A,P(A,(A|B)))={A,P,R(B′),P(A,(A|B′))},由于P(A,(A|B))=P(A,(A|B′)),則R(B)=R(B′),所以可以推出 類似地,還可以構造S2使下式成立 Alice 有一條空間直線L1,Bob 有一條空間直線L2,方程分別為 Alice 和Bob 都想在不暴露自己私有數據的情況下,判斷這兩條空間直線的位置關系. 協議的基本原理Bob 利用平面方程l22的參數構造矩陣B1,矩陣B2以及矩陣B,其中 Bob 將平面方程l21的參數a31,a32,a33,a34發送給Alice(由于經過一條直線的平面有無限多個,所以將其中一個平面參數發送給Alice,Alice 也無法推斷出直線方程).Alice 利用L1,l21的系數構造矩陣A1、矩陣A2以及矩陣A,其中 Alice 和Bob 利用矩陣A1,A2,B1,B2構造矩陣(A1B1)、矩陣(A2B2)以及增廣矩陣(AB),其中 因此,判定空間兩條直線間的位置關系的問題就轉化為矩陣(A1B1)與增廣矩陣(AB)秩的關系.當R(A1B1)=R(AB)=3 時,L1與L2相交于一點;當R(A1B1)=R(AB)=2 時,L1與L2重合;當R(A1B1)=2 且R(AB)=3 時,L1與L2平行;當R(A1B1)=3 且R(AB)=4 時,L1與L2為兩條異面直線.為方便表達,定義如下謂詞: 例如,Alice 有一條空間直線L1,Bob 有一條空間直線L2,方程分別為 Alice 和Bob 利用矩陣A1,A2,B1,B2構造矩陣(A1B1)、矩陣(A2B2)以及增廣矩陣(AB),其中 對矩陣(A1B1)和增廣矩陣(AB)進行初等行變換,將矩陣(A1B1)和增廣矩陣(AB)化為行階梯矩陣(A1B1)′,(AB)′,其中 由此可知,R(A1B1)=2 且R(AB)=3,所以L1與L2平行,輸出P(L1,L2)=2. 協議2保密的計算空間兩條直線間的位置關系. 輸入:Alice 有一條空間直線L1,Bob 有一條空間直線L2. 輸出:P(L1,L2). (1)Bob 將l21的參數a31,a32,a33,a34發送給Alice.Alice 和Bob 調用協議1 中的(1)–(2). (2)Alice 比較R(AB)與R(A1B1)的大小.若R(AB)=4,輸出P(L1,L2)=3;若R(A1B1)=R(AB)=3,輸出P(L1,L2)=0;若R(A1B1)=R(AB)=2,輸出P(L1,L2)=1;若R(A1B1)=2 且R(AB)=3,輸出P(L1,L2)=2. 定理3在半誠實模型下,協議2 是正確的. 證明:證明方法與定理1 的證明類似,是根據矩陣秩的定義和初等變換不改變矩陣的秩保證其正確性. 協議2 的安全性分析協議2 的安全性分析與協議1 的安全性分析類似. 定理4在半誠實模型下,協議2 是安全的. 證明:證明方法與定理1 的證明類似,也可采用構造模擬器的方法. Alice 有一個多項式f(x)=anxn+an?1xn?1+···+a0x0,Bob 有一個多項式g(x)=bmxm+bm?1xm?1+···+b0x0.Alice 和Bob 都想在不暴露自己私有數據的情況下,判斷多項式f(x)是否可以整除g(x).若f(x)可以整除g(x),記f(x)|g(x);若f(x)不可以整除g(x),記f(x)?g(x). 協議的基本原理Alice 利用多項式f(x)中的系數,每一列擴展(m?n)個 0,構造矩陣A(m+1)×(m?n+1),Bob 利用多項式g(x)中的系數構造矩陣B(m+1)×1,如圖3 所示. 因此,多項式整除問題就轉換為矩陣A與增廣矩陣(A|B)秩的關系.若R(A)=R(A|B),則f(x)|g(x);若R(A)R(A|B),則f(x)?g(x).為方便表達,定義如下謂詞: 圖3 矩陣A 和矩陣BFigure 3 Matrix A and B 例如,Alice 有一個多項式f(x)=x?2,Bob 有一個多項式g(x)=x2?5x+6.Alice 利用f(x)中的系數,每一列擴展1 個0,構造矩陣A,Bob 利用g(x)的系數構造矩陣B,Alice 計算出初等變換矩陣P3×3發送給Bob,其中 Bob 收到P后,計算PB得到矩陣B′,其中 Bob 將矩陣B′發送給Alice.Alice 比較矩陣A′與增廣矩陣(A′|B′)秩的大小,其中 由此可知,R(A′)=R(A′|B′)=2,所以f(x)|g(x),輸出P(f(x),g(x))=1. 協議3保密的計算多項式整除問題 輸入:Alice 有一個多項式f(x)=anxn+an?1xn?1+ ··· +a0x0,Bob 有一個多項式g(x)=bmxm+bm?1xm?1+···+b0x0. 輸出:P(f(x),g(x)). (1)Bob 構造矩陣B(m+1)×1,將m發送給Alice. (2)若m (3)Alice 和Bob 調用協議1 中(1)–(2). (4)Alice 進行判斷.若R(A′)=R(A′|B′′),輸出P(f(x),g(x))=1;否則輸出P(f(x),g(x))=0. 定理5在半誠實模型下,協議3 是正確的. 證明:證明方法與定理1 的證明類似,是根據矩陣秩的定義和初等變換不改變矩陣的秩保證其正確性. 協議3 的安全性分析協議3 的安全性分析與協議1 的安全性分析類似. 定理6在半誠實模型下,協議3 是安全的. 證明:證明方法與定理1 的證明類似,也可采用構造模擬器的方法. 集合包含問題Alice 有一個集合A={a1,a2,···,an},Bob 有一個集合B={b1,b2,···,bm}.Alice和Bob 都想在不暴露自己私有數據的情況下,判斷一個集合是否包含另一個集合.若一個集合不包含另一個集合,記(A?B)∩(B?A);若一個集合包含另一個集合,記(A?B)∪(B?A).Alice和Bob 都將集合中的數據用多項式的形式表達出來[20].例如,集合A={1,,3,2},即多項式f(x)=(x?1)(2x?1)(x?3)(x?2).因此,集合包含問題就轉換為多項式整除問題.若(f(x)|g(x))∪(f(x)|g(x)),就是一個集合包含另一個集合;否則不是.具體協議與協議3 類似,本文不予給出. 整除問題Alice 有一個機密數x(x0),Bob 有一個機密數y(y0).Alice 和Bob 都想在不暴露自己私有數據的情況下,判斷一個數是否整除另一個數.若兩個數據不具有整除關系,記(x?y)∧(y?x);若兩個數據具有整除關系,記(x|y)∨(y|x).根據算術基本定理,任一整數z都可以表示為 pi表示第i個素數,即p1=2,p2=3,···,令[p]=Alice 和Bob 利用x,y,[p]構造集合[pA],[pB].例如,數據z=24,即[p]={2,4,8,3}.因此,數的整除判定問題就轉換為多項式整除問題.若(f(x)|g(x))∨(f(x)|g(x)),就是兩個數據具有整除關系;否則不是.具體協議與協議3 類似,本文不予給出. 本文的基礎協議(協議1)本質是通過保密計算增廣矩陣的秩,以此保密判斷矩陣的秩和增廣矩陣的秩是否相等.因此在與其他文獻做對比時,為了統一標準,均以求解矩陣的秩來比較方案的計算復雜性和通信復雜性. 計算復雜性分析文獻[15]求矩陣秩的時候調用了向量比等協議,其計算開銷是n·(mn+2m+2)Me,m,n表示Alice 和Bob 兩個人合作計算一個m維n列矩陣的秩,Me是模指數運算(下同).文獻[16]求矩陣秩的時候需要調用mn次點積協議,計算開銷是m2nMe,m表示參與者個數,n表示每個參與者所擁有向量的維數.在計算復雜性理論中,當模指數運算與普通的運算數量差不多的時候,普通的基本運算所消耗的時間一般可以忽略不計.文獻[15,16]均有復雜的模指數運算,而我們的協議只有簡單的初等變換運算,因此與文獻[15,16]中的協議相比,我們的協議計算復雜性可以忽略. 本文的方案主要利用了矩陣的初等行變換運算,所以分析計算復雜性時,只考慮協議執行中最費時的初等行變換運算,其他運算忽略不計.現以3×3 維的矩陣為例,在我們的實驗條件下求矩陣的初等變換矩陣的計算開銷約3 毫秒,對矩陣進行一次隨機化處理的計算開銷約1 毫秒,總共耗時約4 毫秒.4×4維矩陣求一次初等變換矩陣和隨機化處理的計算開銷約6 毫秒,依次類推,實驗數據顯示求一次初等變換矩陣和隨機化處理的計算開銷是隨著矩陣維數的增長大致線性增長.由于計算開銷與計算設備和計算軟件密切相關,本文假設求一次初等變換矩陣是x毫秒,執行一次m×n維矩陣隨機化處理是h毫秒.本文協議1–3 均需要求一次初等變換矩陣和執行一次矩陣隨機化處理,計算開銷均為(x+h)毫秒. 通信復雜性分析衡量通信復雜度的指標是用協議交換信息的比特數,或者用通信輪數,在安全多方計算研究中通常用輪數.文獻[15]通信輪數是n·(mn+2m+)輪.文獻[16]通信復雜度主要產生在調用點積協議時產生的信息交互,通信輪數為mn2輪.本文中協議1 的通信復雜性是3 輪,協議2 的通信復雜性是4 輪,協議3 的通信復雜性是4 輪,所以本文協議的計算復雜性和通信復雜度都比較低.矩陣的秩計算方案的計算復雜性和通信復雜性比較見表1. 表1 矩陣的秩計算方案的效率對比Table 1 Comparison of all solutions on matrix rank calculation 另外給出本文在應用部分的協議2(空間兩條直線的位置關系)與文獻[21]在效率和安全性方面的分析與比較(見表2).文獻[21]調用了內積協議,其中方案中調用的內積協議總次數和用戶需要進行的模指數運算的次數作為衡量計算復雜性的指標,其它運算忽略不計.模指數運算記為Me. 表2 直線與直線位置關系判定方案的效率對比Table 2 Comparison of solutions on location relation between line and line 實驗仿真由于協議2 和協議3 與協議1 類似,所以實驗仿真只模擬協議1. 操作系統:Windows7(64 位).操作軟件:MATLAB R2014a.語言:MATLAB.協議1:保密的計算矩陣與增廣矩陣秩相等問題.設定:矩陣為方陣,方陣內每一個數據為8 位大隨機數,方陣的維數間隔為1.圖4 描述了協議1 的執行時間隨著方陣維數增長的變化規律. 圖4 協議1 的執行時間隨著方陣維數增長的變化規律Figure 4 Consume time of protocol increases with the dimension of square matrix 由圖4 可知,以毫秒為單位測出的執行時間隨方陣維數的增長大致呈線性增長.綜上所述,協議1–3不僅具有較高的安全性,而且計算雙方的通信代價及計算復雜度都比較低. 本文研究矩陣與增廣矩陣的秩是否相等的問題,設計了一個不需要借助密碼學原語、具有信息論安全、計算復雜性低且通信效率高的安全多方保密計算協議.在保密判斷矩陣和增廣矩陣秩是否相等協議的基礎上,提出了保密判斷兩個多項式是否可以整除的協議,利用該協議可以解決有理數集合包含問題、數的整除問題.本文還提出可以利用矩陣和增廣矩陣秩是否相等保密高效的解決空間直線與直線的位置關系.本文研究的這些問題都是基于半誠實模型的,對于多方保密計算的研究與應用有重要的理論意義,對其他密碼學應用也有一定意義,未來將研究惡意模型下的保密計算矩陣與增廣矩陣的秩是否相等的問題.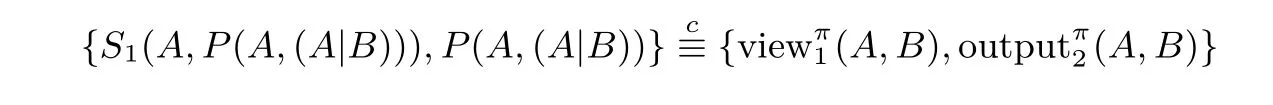
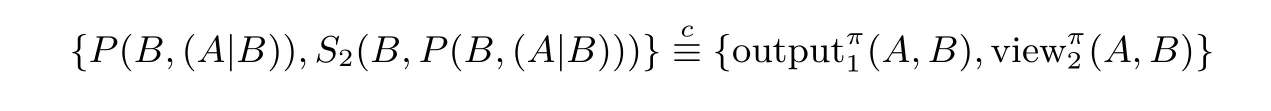
4 空間兩條直線的位置關系
4.1 問題描述
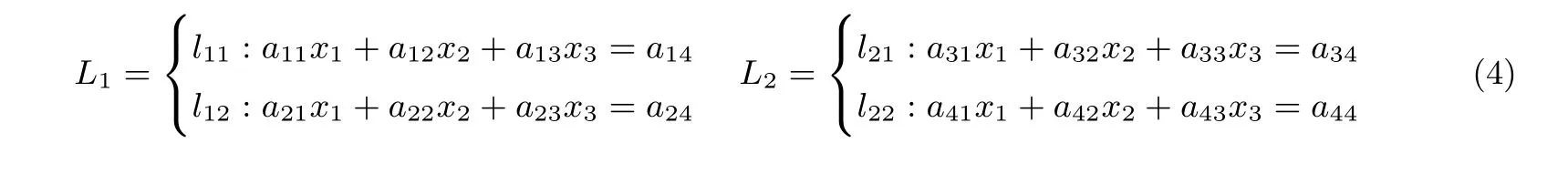
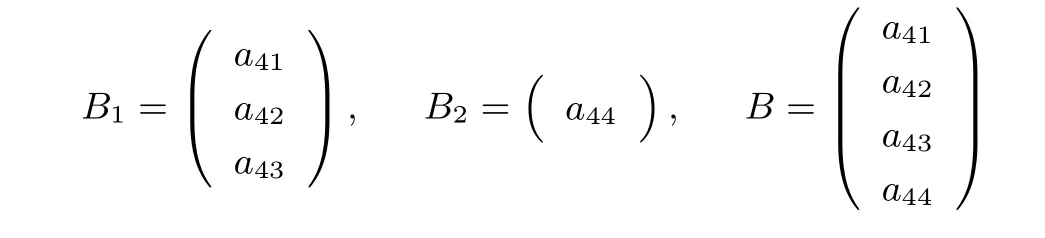

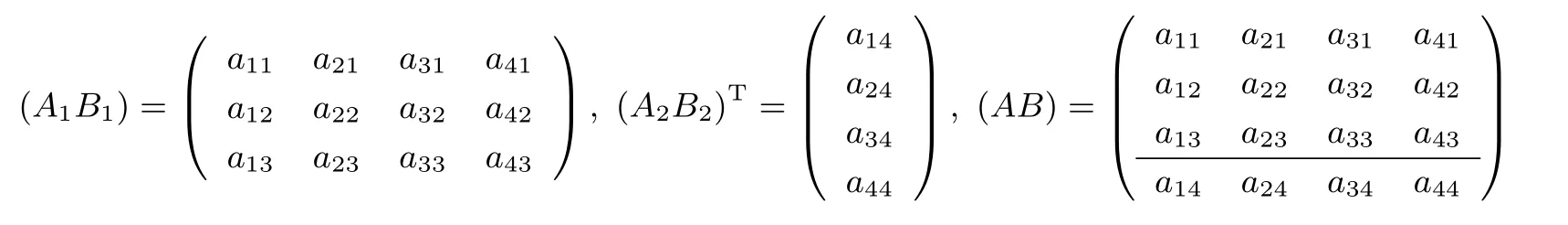

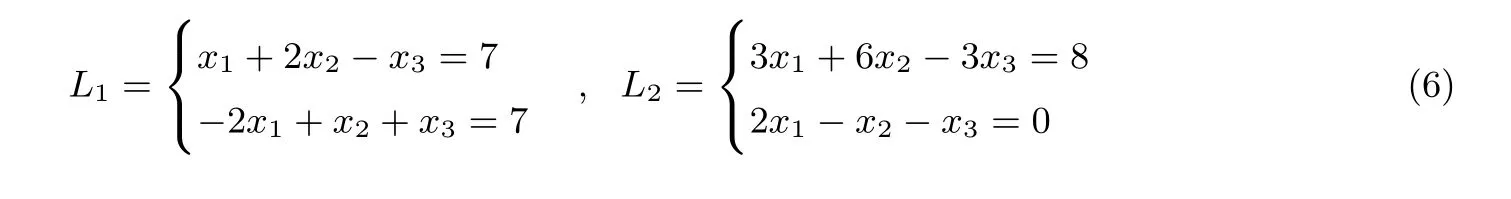

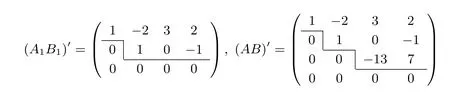
4.2 空間兩條直線的位置關系保密計算方案
5 多項式整除問題
5.1 問題描述


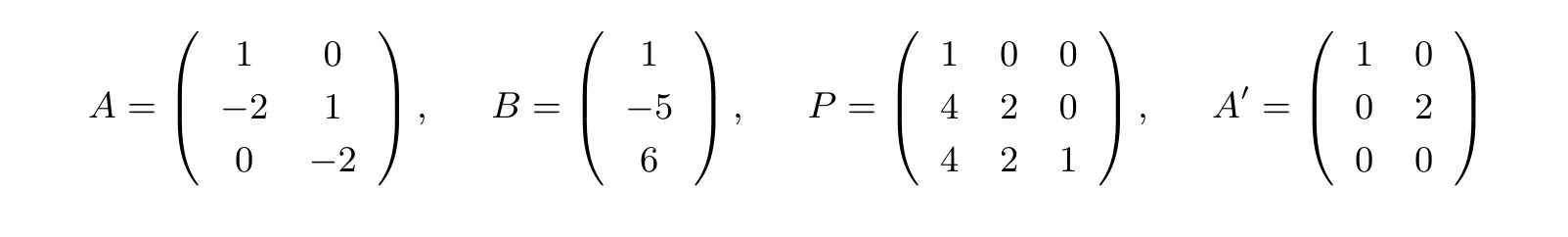
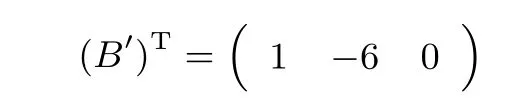
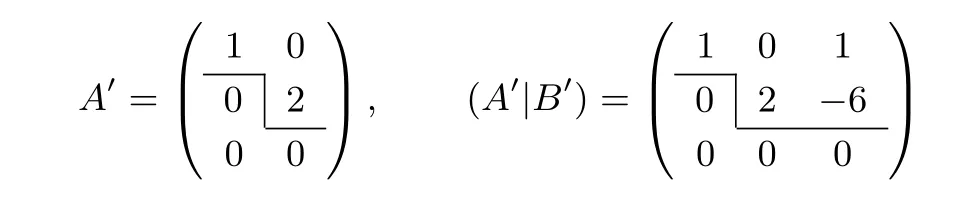
5.2 多項式整除問題保密計算方案
5.3 多項式整除問題的應用
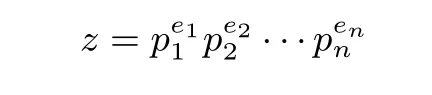
6 性能分析
6.1 效率分析



7 結論

