用差異演化-粒子群混合算法確定含水層參數
段國榮,劉元會
(長安大學 理學院,陜西 西安 710064)
0 引 言
在中國工業快速發展的進程中,水資源問題逐漸增多,地下水是水資源的重要組成部分,地下水資源的評價及開發利用就變得特別重要。含水層參數是進行地下水資源評價和開發利用的基礎數據。開發利用地下水資源時,往往會遇到含水層具有直線供水邊界的情況。標準曲線配線法[1],時間定律法(Law of Times)和拐點法(Method of Inflection Point)[2],非線性最小二乘法[3-4],線性回歸法[5],Su shil K.S.方法[6-7],直線圖解法[8]和割離井法[9-10]等是分析直線供水邊界含水層抽水試驗數據的傳統方法,但此類方法在實際應用中受到一定的限制。近年來,人們廣泛使用智能優化算法來分析抽水試驗數據,求解含水層參數,例如粒子群優化算法[11],混沌人工魚群混合算法[12],遺傳算法[13],改進粒子群算法[14],單純形探索法[15],單純形差分進化混合算法[16],混沌粒子群優化算法[17]和單純形-粒子群混合算法[18]等方法。郭建青,李彥等將粒子群優化算法[11]應用于確定含水層參數,但該算法對粒子數目的大小依賴性很強。袁帆,劉元會等利用單純形-粒子群混合算法[18]計算含水層參數的問題,但計算結果精度不高,且粒子數目的大小和待估參數取值范圍對算法的收斂性有較大的影響。粒子群優化算法[11]操作簡單且易實現,但種群多樣性的缺失使其易陷入局部最優。因此,本研究對粒子群優化算法(PSO算法)進行改進,提供一種差異演化-粒子群混合算法(DE-PSO算法)。將差異演化-粒子群混合算法用于分析直線供水邊界條件下含水層的抽水試驗數據,求解含水層參數,計算觀測孔與虛擬映射井之間的距離。本研究重點討論了該算法的可靠性和有效性,并就待估參數取值范圍對算法收斂性的影響進行數值實驗分析。
1 優化算法簡介
1.1 DE-PSO算法的思想
PSO算法在迭代后期由于種群多樣性的下降存在收斂速度慢,精度差,且易陷入局部最優等問題,利用DE算法[19-21]中的3種遺傳操作,即變異操作,交叉操作和選擇操作,變異粒子中各個體的歷史最優位置,不僅能使種群保持一定的多樣性,進而避免出現早熟或停滯的現象,而且能保持PSO算法迭代前期收斂速度快的優點。本研究引入聚集度因子[22]來確定粒子個體歷史最優位置是否需要進行變異
(1)
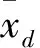
1.2 DE-PSO算法的步驟
步驟1:初始化算法的相關參數;確定粒子個數N,搜索空間維度D,最大迭代次數gen,最優累計次數K[23],各粒子的初始位置及初始速度、搜索空間的上下限、縮放因子F,交叉概率CR,初始化循環迭代次數t和最優累計次數k,聚集度因子Fa,收斂精度e1以及計算相似度e2[23].
步驟2:計算初始種群中每個粒子的適應度值,保存粒子局部和全局最優位置,最優值。
步驟3:若當前迭代次數小于最大迭代次數gen且當前的最優累計次數k小于最優累計次數K,則進入循環,否則輸出最優結果。
步驟4:更新每個粒子的速度和位置,且進行粒子個體最優更新及群體最優更新。
步驟5:計算粒子的聚集度因子Fa,若Fa大于所給定的閾值,則進入步驟6,否則返回步驟4.
步驟6:利用DE算法中的變異、交叉、選擇等遺傳操作,變異粒子中各個體的歷史最優位置,并更新粒子歷史最優位置。
步驟7:如果全局最優解小于e1且全局最優解的誤差小于相似度e2,則k=k+1,否則返回步驟3繼續執行。
步驟8:輸出結果。
2 目標函數與控制條件
2.1 降深表達式
由地下水動力學[24-25]中的迭加原理可知,含水層中任一位置的降深可以由2部分迭加得到,即在直線供水邊界條件下,虛擬映射注水井注水和抽水實井抽水分別在該位置產生降深的疊加。虛擬映射注水井、抽水實井和直線供水邊界的位置關系[5],如圖1所示。
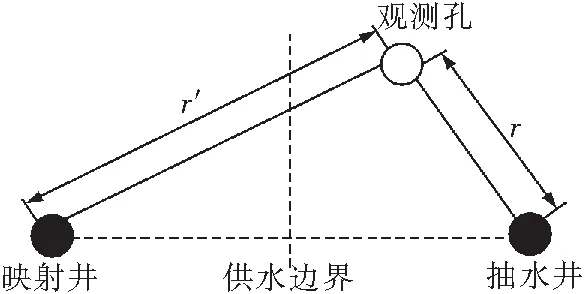
圖1 直線供水邊界條件下抽水實井和虛擬映射注水井的位置關系Fig.1 Location relationship between the pumping well and the virtual mapping injection well in linear pervious boundary
該情況下,含水層中任一位置的降深表達式[26]如下
s=s1+s2=[w(u1)-w(u2)]Q/4πT
(2)
式中Q為抽水流量,L3/T1;T為含水層的導水系數,L2/T2;s1為直線供水邊界條件下實井抽水引起的降深,L;s2為直線供水邊界條件下虛擬映射注水井引起的降深,L;w(u1)和w(u2)分別為相應的抽水實井和虛擬映射注水井的井函數,無量綱,其表達式分別為
(3)
其中無量綱時間參量u1和u2的表達式分別為
(4)
式中t為抽水持續時間,T;S為儲水系數,無量綱;r為抽水實井與觀測井的距離,L;r′為虛擬映射井與觀測井的距離,L.
③有法不依、執法不嚴的問題比較突出。由于管理體制不順,違反《塔里木河水資源管理條例》、自治區批準的水量分配方案、水量調度管理辦法,不執行水調指令,搶占、擠占生態水,不按塔里木河規劃確定的輸水目標向塔里木河輸水的現象時有發生。塔里木河干流水權及生態用水水權得不到依法保護,塔管局由于現行的管理權限所限,難以依法進行處罰。
由式(3)可知,在計算水位降深值時,需要對井函數進行廣義積分求解。采用R.Srivastava給出的近似表達式[27]進行計算
W(u)=-Inu+a0+a1u+a2u2+a3u3+a4u4+a5u5,u≤1
(5)
(6)
式中a0=-0.577 72,a1=0.999 99,a2=-0.249 1,a3=-0.055 19,a4=-0.009 76,a5=0.001 08,b0=0.267 77,b1=8.634 76,b2=18.059 02,b3=3.958 50,c0=3.958 50,c1=21.099 65,c2=25.632 96,c3=9.573 32.
2.2 目標函數的構成
采用DE-PSO算法求解含水層參數時,待估參數向量θ=(T,S,r′)應滿足降深觀測值與計算值的方差達到最小,構造如下目標函數
(7)
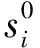
2.3 算法參數控制
聚集度因子Fa∈[0,2],根據多次試驗結果,本研究選取Fa的閾值Fa=1.3,交叉概率CR∈[0,1],縮放因子F∈[0,2],粒子數目維度N=20,最大迭代次數gen=200,根據文獻[28],選取含水層導水系數T∈[2.5,3.5] m2/min,儲水系數S∈[0.050,0.070],觀測井到虛擬映射井的距離r′∈[100,130] m,取e1=5×10-5,e2=10-9,K=10.
3 算例
3.1 不同方法計算結果的比較
表2中給出了DE-PSO算法和相關文獻中的其他方法對含水層參數的計算結果。
從表2可知,DE-PSO算法估計含水層參數值及觀測井與虛擬映射井之間的距離與其他方法接近,且由該算法求得的φ(θ)精度高于其他方法,因此,DE-PSO算法所求結果是可靠的。
3.2 算法的有效性
圖2表示的是DE-PSO算法的程序運行100次目標函數值的分布情況。從圖2能夠看出,在DE-PSO算法的程序運行100次的過程中,有91次成功,其收斂率達到91%.由此可知,DE-PSO算法的收斂率較高,具有高效性。因此,利用DE-PSO算法能有效地估計含水層參數。
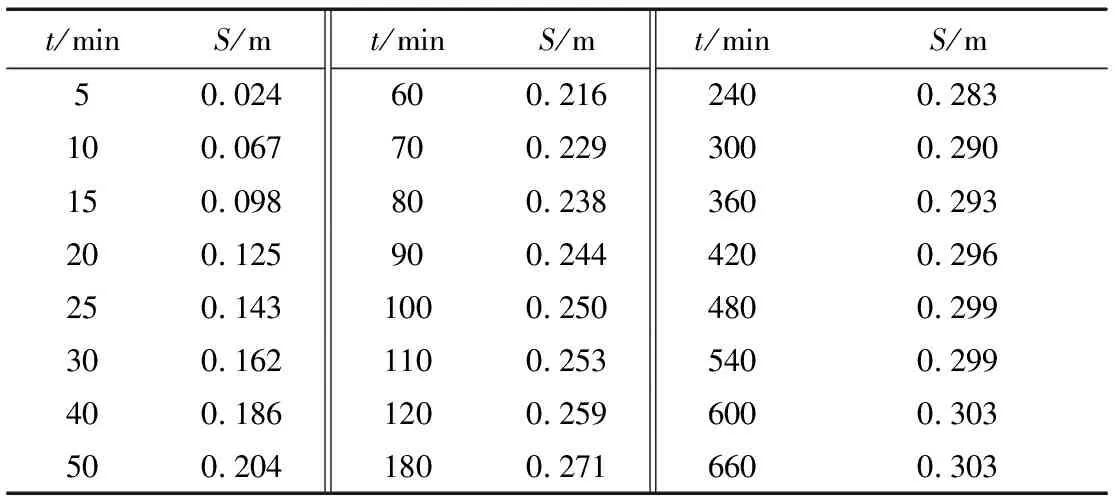
表1 原始抽水試驗數據

表2 不同方法的計算結果
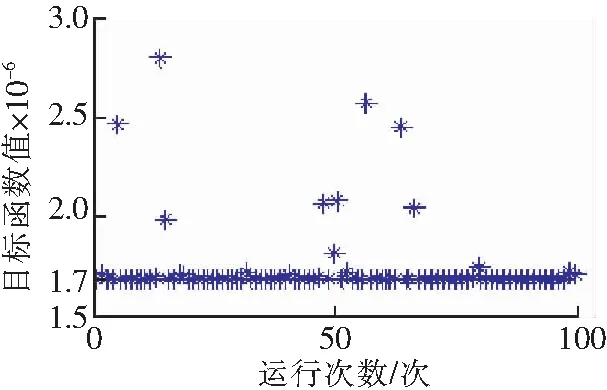
圖2 DE-PSO算法運行100次目標函數值分布Fig.2 Distribution of the objective function value after 100 runs of DE-PSO algorithm
3.3 算法的穩定性
表3是在其他條件不變,待估參數取值范圍的上限擴大到原來的2,4,8,10,12和14倍的情況下,利用DE-PSO算法求得含水層參數及觀測井與虛擬映射井之間距離的估計值。由表中信息可知,隨著待估參數范圍的增大,DE-PSO算法具有很好的收斂性,當待估參數取值范圍的上限擴大到原來的14倍時,收斂率高達97%,且得到目標函數值基本一致,即DE-PSO算法對初值選取的敏感性低,尋優能力強,穩定性好。
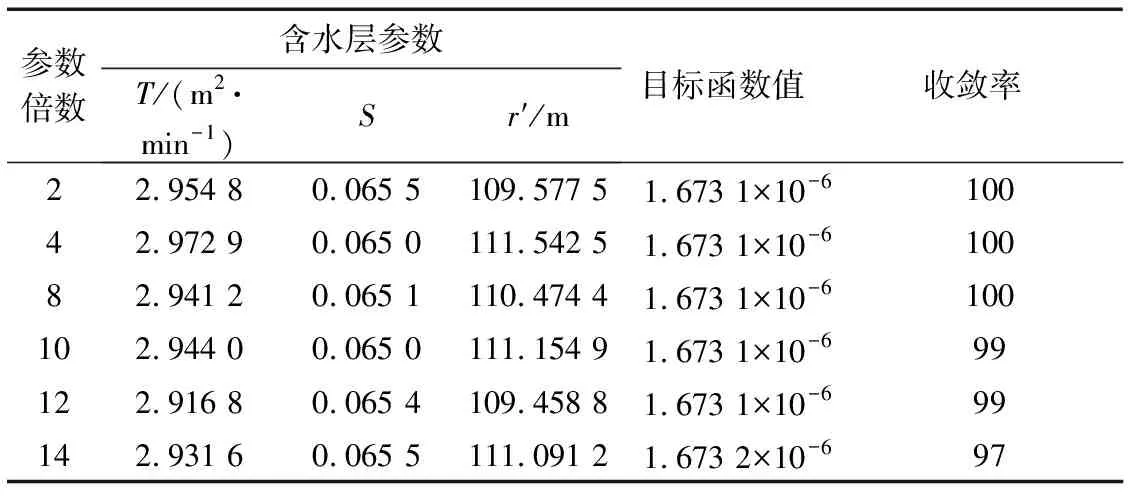
表3 不同參數取值范圍下的計算結果
4 結 論
1)DE-PSO算法得到的目標函數值φ(θ)精度高于其他方法。
2)估計含水層參數時具有較好的收斂性,具有較高的精度。
3)待估參數初始取值范圍的放寬對DE-PSO算法的收斂性影響較小,即DE-PSO算法對初始取值范圍選取的敏感性低,尋優能力強,穩定性好。因此,DE-PSO算法是分析抽水試驗數據,求解含水層參數和計算觀測孔與虛擬映射井之間距離的有效方法。

