Bloch型空間到調和權Dirichlet型空間的復合算子

劉佐靈

（汕頭大學理學院，廣東 汕頭 515063）

0 引言

在Cowen和MacClue的著作中[1]，具體討論了復合算子在某些函數空間上的有界性和緊性的問題.在文獻[2]中，解決了經典Hardy 空間和Bergman空間上的復合算子的有界性緊性問題.Shapiro 在文章[3]中首次引入了復合算子的本性范數.近年來，復合算子在各類函數空間上的問題得到了豐富發展.其中與Bloch空間相關的復合算子的文章有文獻[4-10].與Bloch 空間相關的關于復合算子的本性范數刻畫的文章有文獻[11-13].本文主要也是考慮從Bloch 型空間出發到新一類空間的復合算子，主要討論在其上的有界性、緊性和本性范數的問題.

2005年，烏蘭哈斯在文獻[8]中討論了Bloch 空間到Qk空間的緊性問題.2007年，Marko Kotilainen 在文獻[5]中研究了復合算子從Bloch 型空間到Qk型空間的有界性和緊性問題.2009年，Jordi Pau 在文獻[7]中考慮了復合算子從Bloch 型空間到Qk型空間的本性范數的問題.從以上文章中受到啟發，本文主要考慮復合算子從Bloch 型空間到調和權Dirichlet 型空間上的有界性、緊性和本性范數的問題.

1 準備知識

如果f∈H（D），且范數定義為

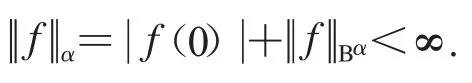
其中

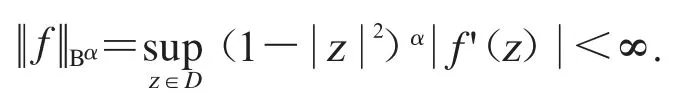
1991年，S.Richter 在文獻[14]中引入了調和權Dirichlet 型空間D（μ）.設μ 為圓周T 上的正Borel 測度，其中

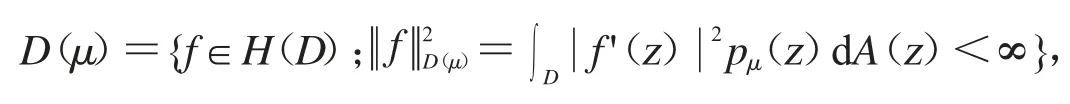
而dA 為單位圓盤上的Lebesgue 測度，其中

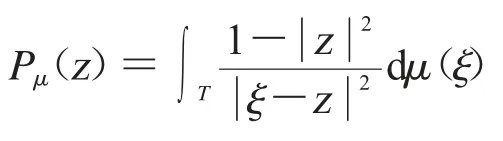
是在單位圓盤D 上關于μ的Poisson 積分.對Dirichlet 空間感興趣的讀者可以學習專著[15].

注：如果存在兩個常數C1和C2使得C1A2≤A1≤C2A2，那么我們就說A1和A2等價，記作A1≈A2.Bx記作Banach 空間上的單位球.

2 引理及主要結果及其證明

引理2.1[16]設α＞0 和為缺項級數，存在常數C＞1 和所有K∈N，有nk＋1≥Cnk.那么

（1）f（z）∈Bα當且僅當

引理2.2[17]設0＜α＜∞，如果{nk}是一個遞增的正整數數列且對所有k的都滿足設0＜p＜∞，那么存在一個只和有關的常數A，使得

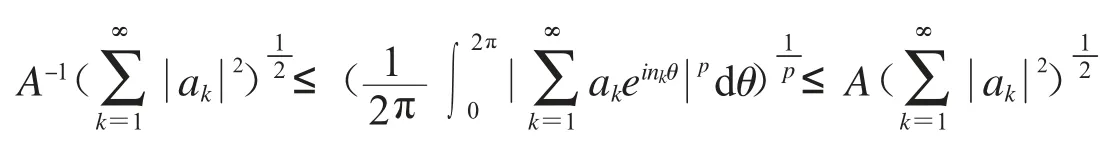
成立，其中{nk}為復平面上的任意數列.

定理2.3 設φ 為單位圓盤上的解析自映射，那么如下敘述彼此等價：

（1）Cφ:Bα→D（μ）是有界的；

證明：我們首先證明由（3）推出（1）.對于所有的f∈Bα我們有

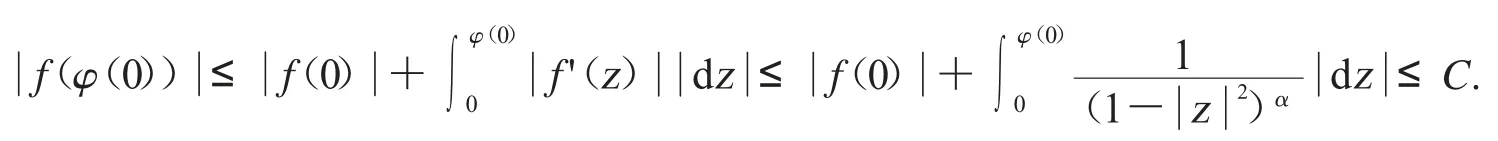
接下來我們證明對所有的f∈Bα且限定時，有如果f∈Bα，我們有

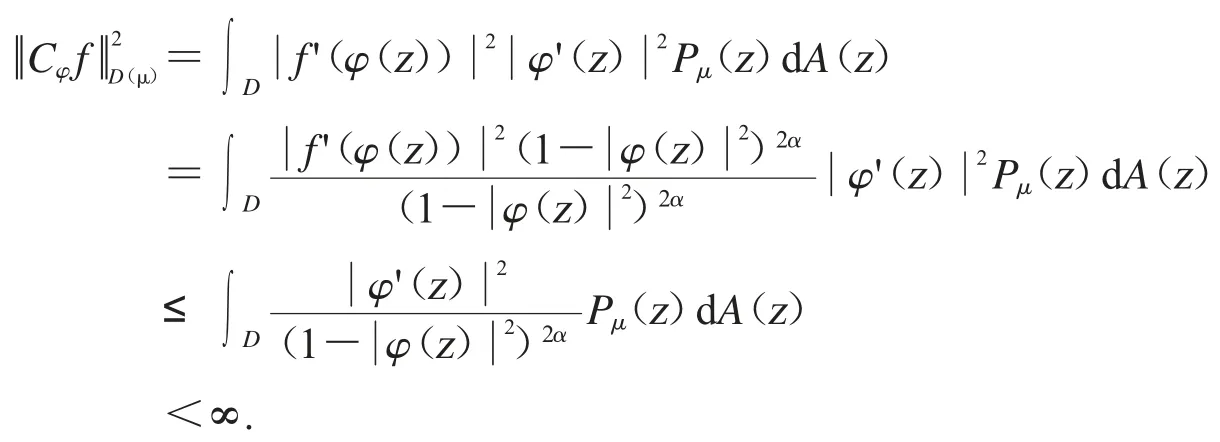
從而證明了（3）推出（1）.

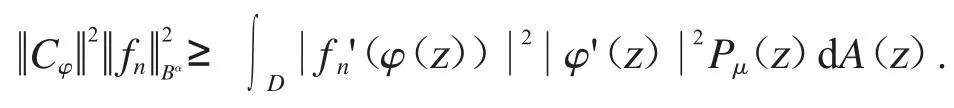
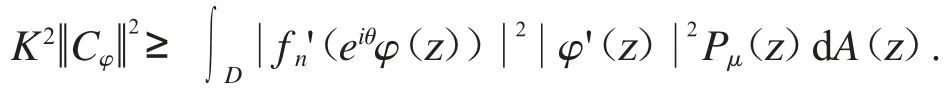
不等式的兩邊都對θ 進行積分和應用Fubini’s 定理可得

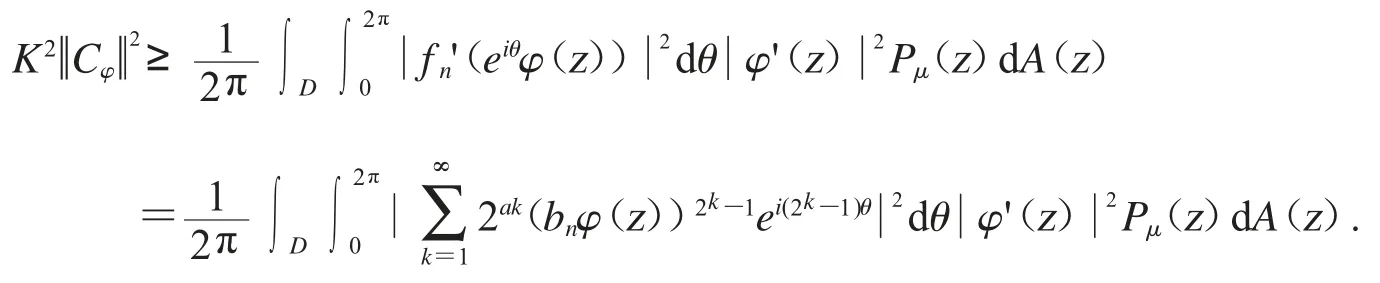
應用引理2.2 可得

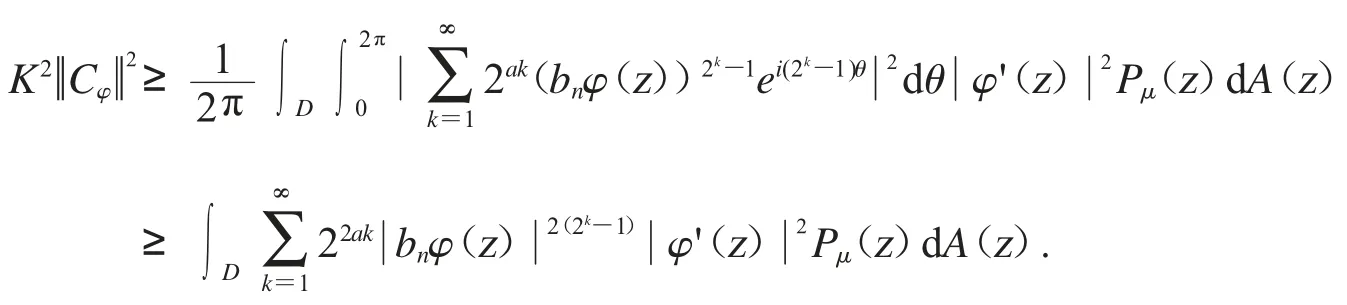
注[9]：其中對任意的r∈（0，1）和α＞0 有

所以我們可得

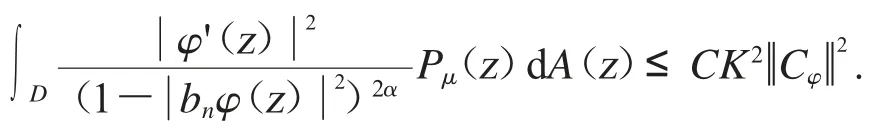
應用Fatou’s 引理可得

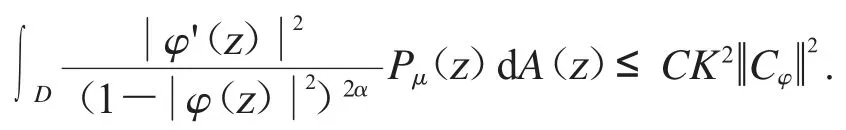
從而由（2）推導得（3）.

引理2.4 設φ 是單位圓盤D 上的解析自映射.那么Cφ:Bα→D（μ）是一個緊算子當且僅當Cφ:Bα→D（μ）是有界的，且對于Bα中的任意有界序列{fn}，若{fn}在單位圓盤D的任意緊子集上，當n→∞時一致收斂到0，有

證明類似于[1]中的命題3.11，在此省略證明.

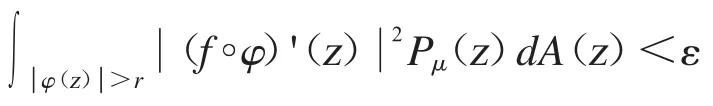
成立，其中0＜δ＜1.

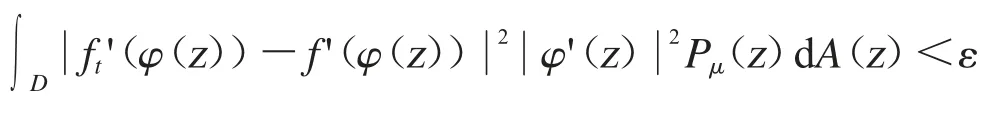
成立.對任意的r∈（0，1）應用三角不等式，可得

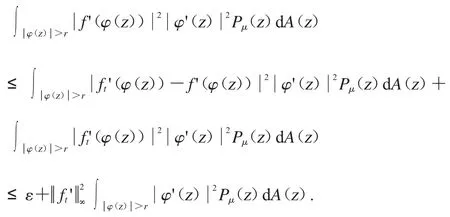
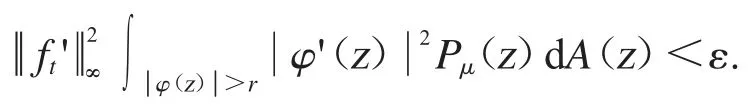
設fn（z）＝nα－1zn.我們可知在D 的緊子集上一致收斂到0.因為Cφ是緊算子，我們可得因此，對任意的ε＞0 和存在一個整數N＞1，使得對任意n＞N 時有

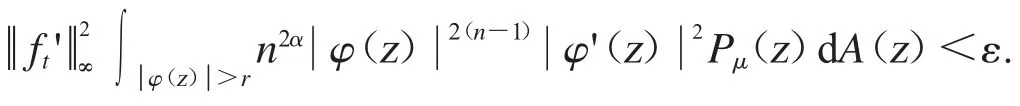
給定r∈（0，1），從上面的公式可得

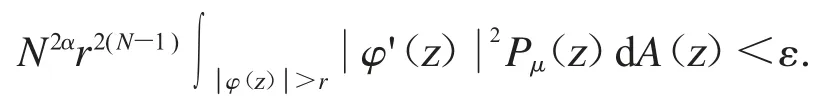
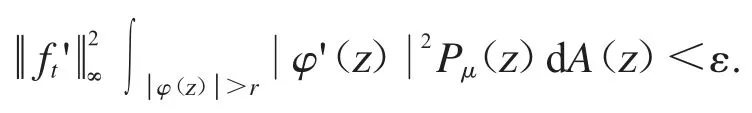
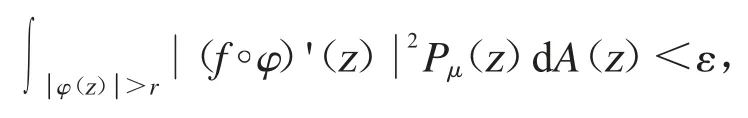
其中δ＜r＜1.

我們完成命題的證明是通過證得δ＝δ（ε，f）是和f∈BBα0無關的.因為Cφ是緊的，Cφ在D（μ）中是相對緊的.因此，存在使得對任意的ε＞0，我們可以選擇fi（1≤i≤n）滿足

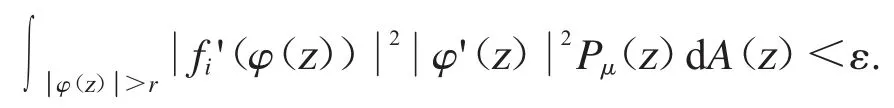
應用三角不等式可得

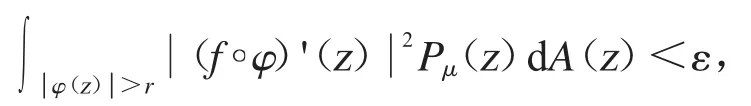
其中δ＜r＜1.所以命題2.5 證明完畢.

定理2.6 設φ 為單位圓盤D 上的解析自映射.那么如下敘述彼此等價：

（1）Cφ:Bα→D（μ）是緊算子；

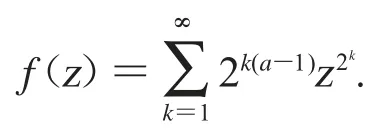
從引理2.1 可知f（z）∈Bα.設在D 上選取一個序列{an}，且當n→∞時，有對所有的n∈N，設gn（z）＝g（anz）.對設gn，θ（z）＝gn（eiθz）.我們可以很容易知道gn，θ（z）∈BBα0，用gn，θ去代替命題2.6 中的函數f 和對dθ 進行積分，應用引理2.2 和Fubini’s 定理，可得

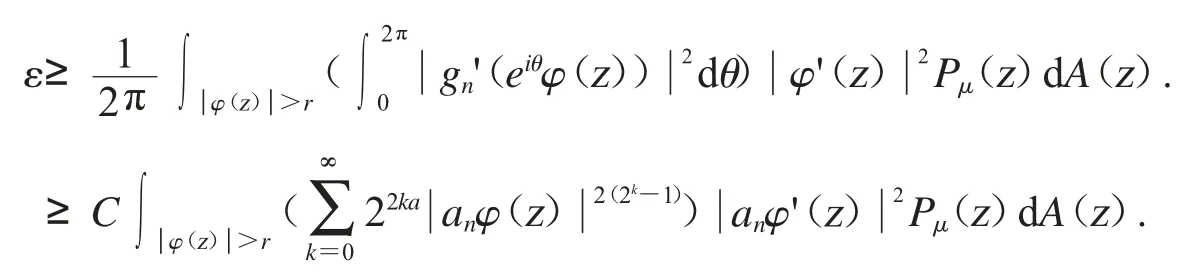
從文獻[9]或[10]中，我們可以知道

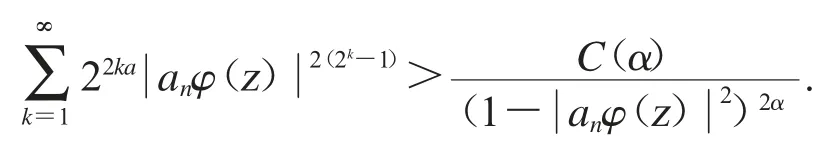
其中C（α）是只跟α 有關的常數.因此，對于充分大的n 和δ＜r＜1，可得

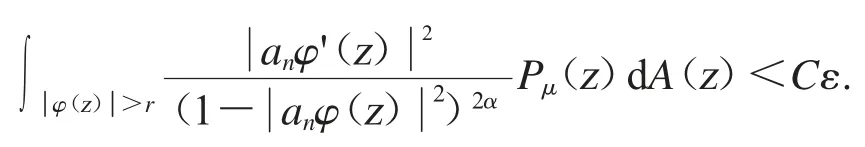
應用Fatou’s 引理，可得

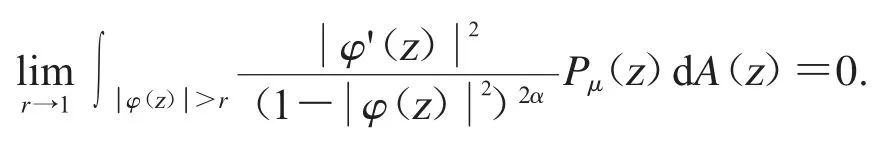
從而證明了由（2）推導出（3）.

現在我們證明（3）推出（1）.假設條件（3）成立，我們可以很容易檢驗Cφ:Bα→D（μ）是有界的.設我們只需要證明在D（μ）中有收斂的序列.設{fn}在D 的緊子集上一致收斂到0 和我們可以知道在D 的緊子集上也是一致收斂到0.如果我們可以證明那么我們將完全證明復合算子Cφ是緊算子.因為條件（3）成立，對于ε∈（0，1）所以存在r∈（0，1）使得對所有的函數fn有

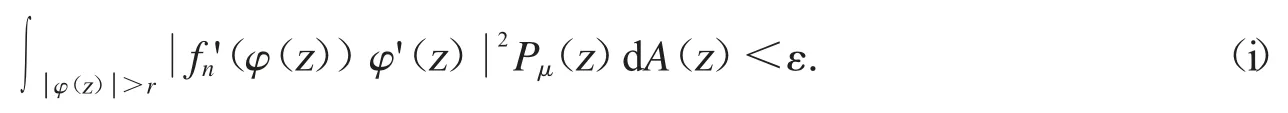
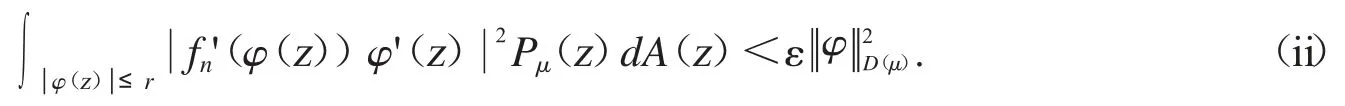
聯合（i）和（ii）式.當n＞N 時，可得

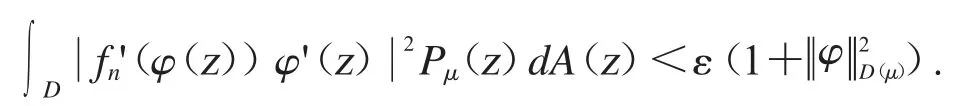
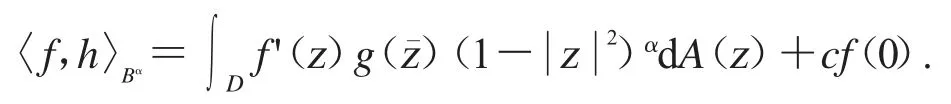
式子成立.

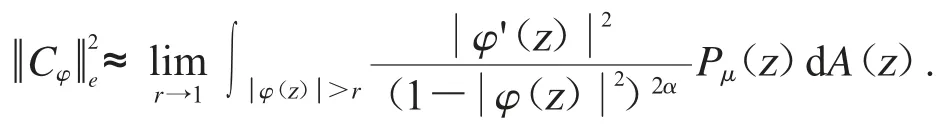
特別地，復合算子Cφ是緊算子，當且僅當

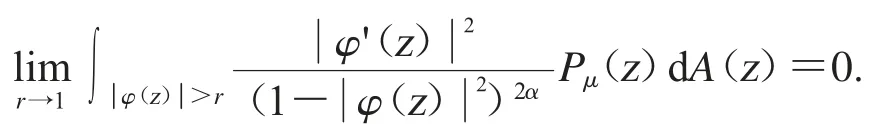
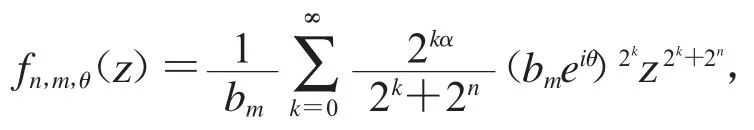
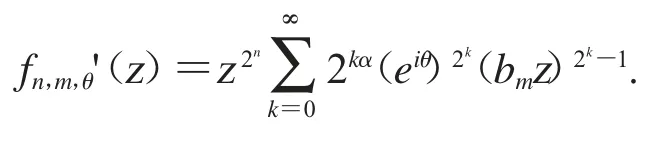
因為

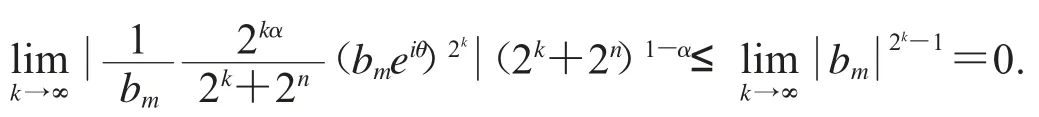
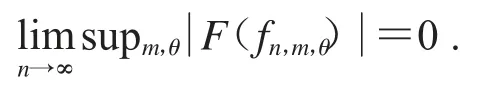
在此，如果S:Bα→D（μ）是任意的緊算子，可得

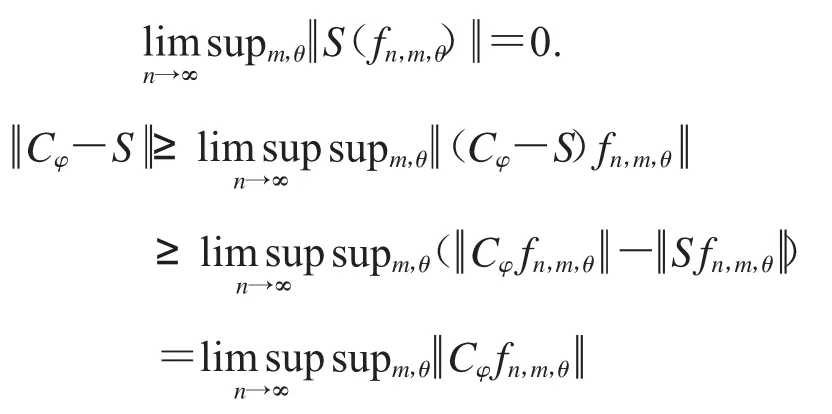
給定ε＞0 存在N∈N 使得n≥N 時有

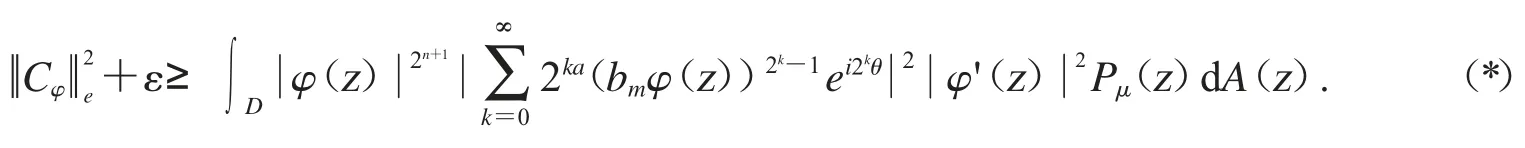
從文獻[7]中，我們可以知道對所有的z∈D 如果n 和m 充分大，時.

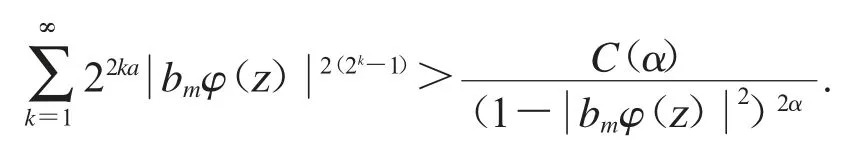
在（*）式上，兩邊都對θ 進行積分，應用Fubini’s 定理和引理2.2 可得

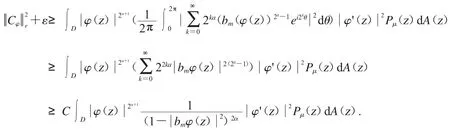
因此，應用Fatou’s 引理可得

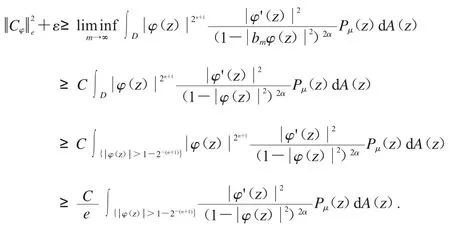
從而可得

因此可得

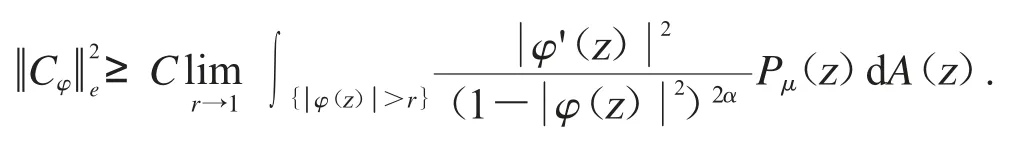
所以我們證明了下界估計.

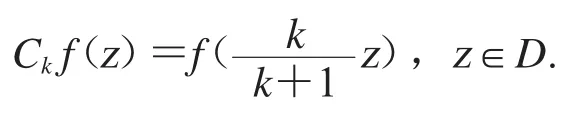
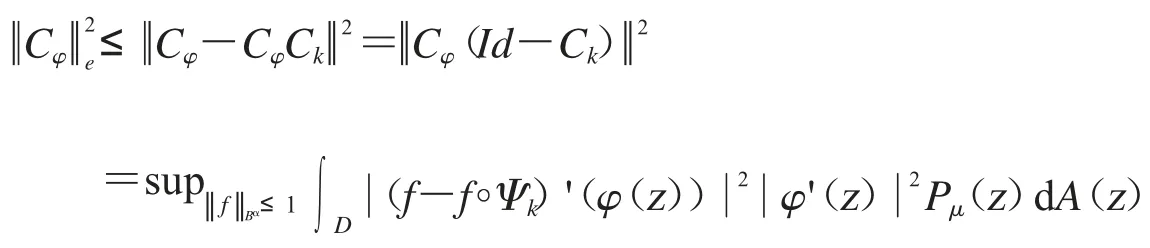
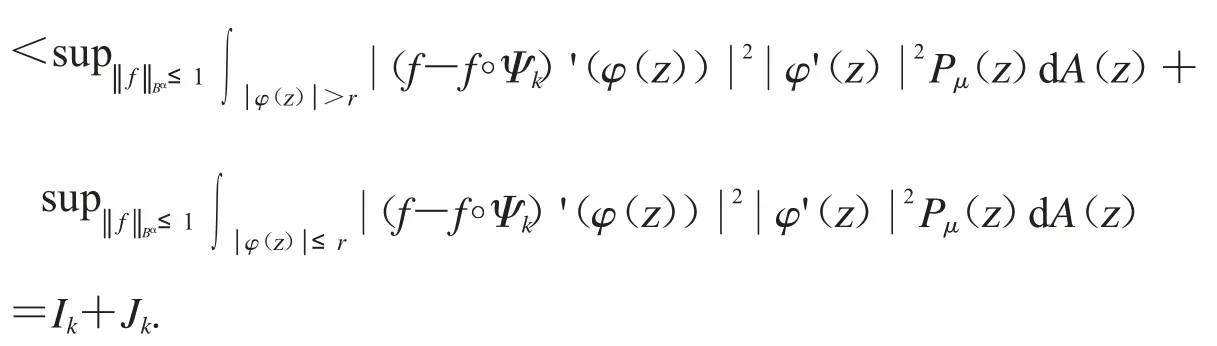
其中固定r∈（0，1）.先估計第一項Ik.設和z∈D 可得

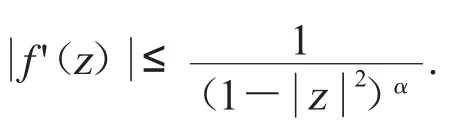
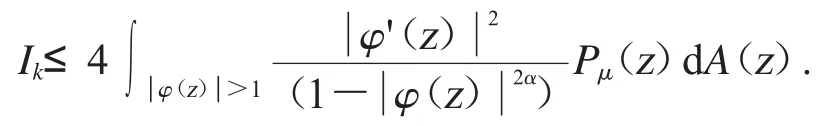
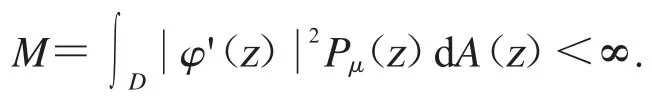
因此

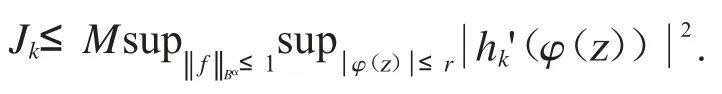
因為hk在D 的緊子集上一致收斂于0，所以我們可知hk'在D 的緊子集上也一致收斂于0.因此可得

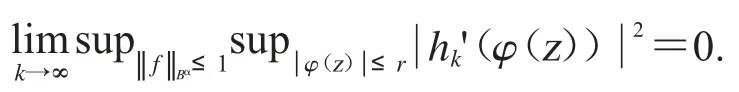
綜上可得

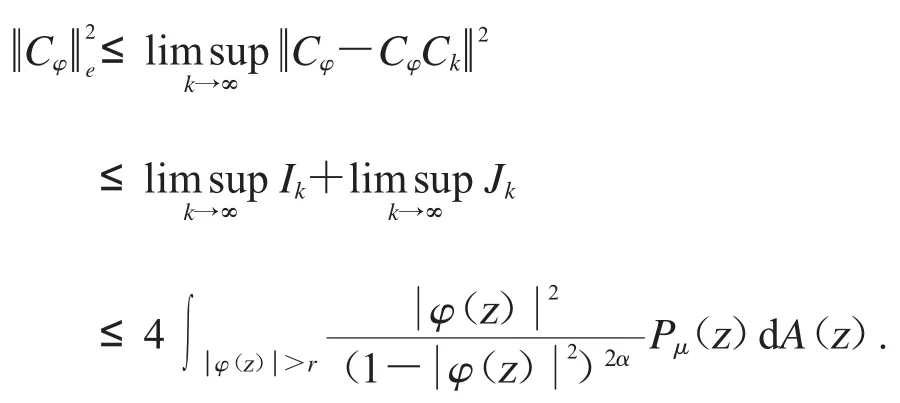
定理證明完畢.