軟件無線電的GNSS干擾盲識別系統

楊燕梅，郎榮玲，葉萬洋

（北京航空航天大學 電子信息工程學院，北京 100191）

0 引言

由于全球衛星導航系統（global navigation satellite system， GNSS）處于復雜的無線環境中，經常受到各種不同干擾信號的影響，這些干擾信號直接影響導航接收機的性能，甚至使其不能工作。因此在接收機中一般需要對接收的信號進行抗干擾，但是由于不同的干擾信號對導航信號的影響不同，所采用的抗干擾算法不同。比如在利用功率反演算法抗脈沖干擾時，由于協方差矩陣存在不穩定性，會導致抗干擾算法失效。但是在抗窄帶干擾以及單頻干擾時，功率反演算法卻有很好的效果。而如果在抗干擾算法之前對干擾進行監測，估計出干擾信號的類型和參數，例如脈沖干擾的周期和占空比，則可以很好地利用功率反演算法進行抗干擾。因此為了保證衛星導航系統的穩定工作，對干擾信號調制類型進行識別及參數估計具有重要的意義。

根據經驗和文獻資料調查發現，針對GNSS的干擾的類型包括數字、模擬、掃頻和脈沖干擾等多種形式，因此GNSS干擾識別是一種缺乏先驗知識的數字調制方式、模擬調制方式及脈沖信號的混合識別。因此研究復雜環境下GNSS干擾盲識別技術是具有重要意義的。

目前無線通信信號的調制體制識別主要分為2大類：基于最大似然假設檢驗方法和基于特征提取的模式識別方法。

基于最大似然假設檢驗的方法的優點在于，它理論上可以保證在貝葉斯最小誤判代價準則下得到最好的分類結果，但其局限性也很明顯，即需要有更多的先驗知識。在沒有先驗知識的條件下，它的復雜性和計算量較大，無法保證系統實時分類，工程應用性較差。

基于特征提取的模式識別方法主要包括2個步驟：特征提取和分類器的設計。特征提取的方法主要分為3大類：

1）基于時間域的特征提取。文獻[1]首次提出利用希爾伯特變換得到信號瞬時幅度、瞬時相位和瞬時頻率，利用瞬時幅度、瞬時相位和瞬時頻率的2階矩以及 2階中心距來對信號進行特征提取，實現了模擬幅度調制，單邊帶、雙邊帶幅度調制以及調頻信號的分類；文獻[2]實現了數字調制信號MASK、MPSK、MFSK的分類；文獻[3]同樣利用希爾伯特變換得到的信號的瞬時幅度、頻率和相位等信息，以人工神經網絡作為分類器，實現數字調制信號（ASK/2FSK/4FSK/BPSK/ QPSK）和模擬調頻和調幅信號的識別。這種基于時間域的特征提取的方法實現簡單，在高信噪比下特征易于提取，且特征具有明顯的物理意義，但這種提取方法受噪聲影響較大。

2）基于統計域的特征提取。統計域的特征主要是利用高階累積量，主要包括3階累計量和4階累計量：文獻[4]實現了利用高階累積量完成數字調制信號（BPSK/QPSK/ 16QAM/32QAM）分類；文獻[5]利用高階累積量實現了 4ASK、8ASK、BPSK、QPSK、8PSK、16QAM、32QAM、256QAM的分類；但利用提取高階累積量，需要將接收到的信號下變頻到基帶信號，這就需要精確的估計載頻，通常載頻的估計會有一定的誤差，于是文獻[6]提出了改進的方法，無需下變頻，實現了BPSK、QPSK、OQPSK、4PAM、8PSK、8QAM、16QAM、32QAM的分類；文獻[7]將高階累積量與支持向量機相結合，在信噪比為4 dB時，識別的正確率可以達到98 %；文獻[8]除了實現4ASK、8ASK、BPSK、QPSK、8PSK、16QAM 的識別，還實現了 MFSK（2FSK、4FSK、8FSK）的識別。利用高階累積量的最大優勢是對于加性的高斯白噪聲具有很好的抗干擾性能。

3）基于變換域的特征提取。基于循環譜的特征提取是變換域特征提取的一種主要方法，不同的調制信號類型的頻譜特征可能相同，但對于不同的調制信號類型循環譜都不同。文獻[9]中通過估計不同調制信號的循環譜，在循環譜域提取提取 6個特征參數，實現 AM、DSM、VSB、SSB、ASK、FSK、PSK、MSK、QPSK的調制識別；文獻[10]利用高階累積量與循環譜域的特征參數相結合，首先利用高階累積量將數字調制信號分為{BPSK，2ASK}、{QPSK}、{2FSK， 4FSK}、{MSK}和{16QAM，64QAM}5類。然后利用高階累積量以及循環譜對{OFDM}、{16QAM， 64QAM}、{2ASK，BPSK}及{2FSK，4FSK}進行識別；文獻[11]中通過估計不同調制信號的循環譜，并將神經網絡作為分類器，實現了 BPSK/QPSK/ FSK/MSK的分類識別。基于循環譜特征提取的方法的優勢是對于不同的調制信號類型會有不同的循環譜，區分度明顯，且抗加性高斯白噪聲的性能較好，但計算量較大，不適合在工程中做實時分類。

文獻[12-13]中對調制信號做連續小波變換，實現了BPSK、2FSK、QAM、MSK、ASK信號類型的分類；文獻[14]中同樣利用小波變換實現了BPSK、2FSK、QAM、MSK、ASK信號類型的分類；文獻[15]利用改進的尺度縮放優化小波變換算法，實現了 2ASK、4ASK、8ASK、16QAM、64QAM、128QAM的分類。由于Haar連續小波變換技術可以實現碼元內小波系數恒定不變，但不同的調制類型碼元內的小波系數可能不同，并且小波系數在變換點處發生突變，利用這一特點來實現不同調制類型的分類，同時它對于噪聲也非常敏感，在低信噪下，識別率較差。

此外還有基于譜分析的特征提取：文獻[16]中利用信號譜、平方譜以及 4次方譜實現了 BPSK/QPSK/OQPSK/π/4QPSK/MSK/FSK/FM/CW 的分類識別，信噪比大于12 dB時總體識別率達到95 %。

分類的方法大致有2類：傳統的基于決策樹的分類器；基于人工智能的分類器。傳統的分類器每個特征都需要對應設置一個判決門限，而判決門限的選取對識別的正確率影響很大；其次每個判決節點只能使用一個特征判決，這就導致識別的正確率不僅與特征量使用的先后次序有關，而且完全取決于每個特征的單次正確判決率。而人工智能的方法對判決門限的選取是自適應的，而且它每次判決都需要使用全部的特征向量，這就使得系統的識別成功率大大提高。

GNSS所處電磁環境復雜，多種類型干擾并存，并且還鮮有能應用于導航系統的干擾監測產品。軟件無線電具有高度的靈活性、通用性和功能模塊化等特點，同時也是一種新的無線電系統體系結構，以開放性、可擴展、結構精簡的硬件為通用平臺。因此本文主要基于軟件無線電架構，搭建了GNSS干擾盲識別系統。本系統可識別多干擾并存環境下的干擾類型以及每種類型干擾的參數。

1 系統設計

GNSS盲識別系統的總體結構如圖1所示。

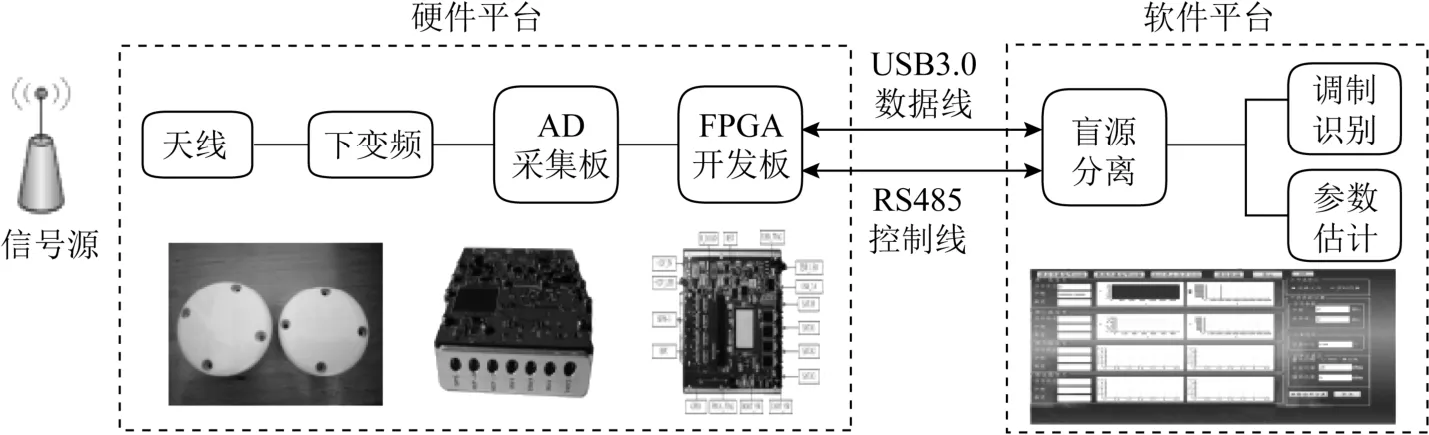
圖1 衛星導航自適應干擾盲識別系統

硬件平臺由天線，下變頻器、AD采集板、USB3.0接口、RS485接口、FPGA芯片以及上位機組成。

硬件平臺完成信號采集并將采集的信號傳輸至上位機。在本系統中下變頻和 AD采用選用芯片AD9361完成，AD9361具有2個相互獨立的下變頻通道以及 12位模數轉換器（analog-to-digital converter，ADC）。系統中的FPGA采用Xilinx K7系列芯片。USB3.0作為數據總線用于傳輸數據、RS485作為控制總線傳送控制指令。

軟件部分在上位機上實現，包括盲源分離、調制體制識別、調制參數識別3個功能。盲源分離模塊主要任務是將混疊的干擾信號進行分離，本系統中采用的是復數快速獨立分量分析法實現混合信號的盲分離。調制體制識別模塊的任務是識別分離后的每一路信號的調制功能。調制參數識別的任務是識別每種調制體制的中心頻點、帶寬、占空比等參數。本論文主要研究干擾信號調制體制識別以及參數識別技術。

2 干擾自適應盲識別方法

本論文基于特征參數的調制識別方法是利用二叉樹的分類方法把每個特征參數的值與預先設定的閾值進行比較，通過決策樹判決的方式實現多種調制方式的分類與識別，具體過程如圖2所示。

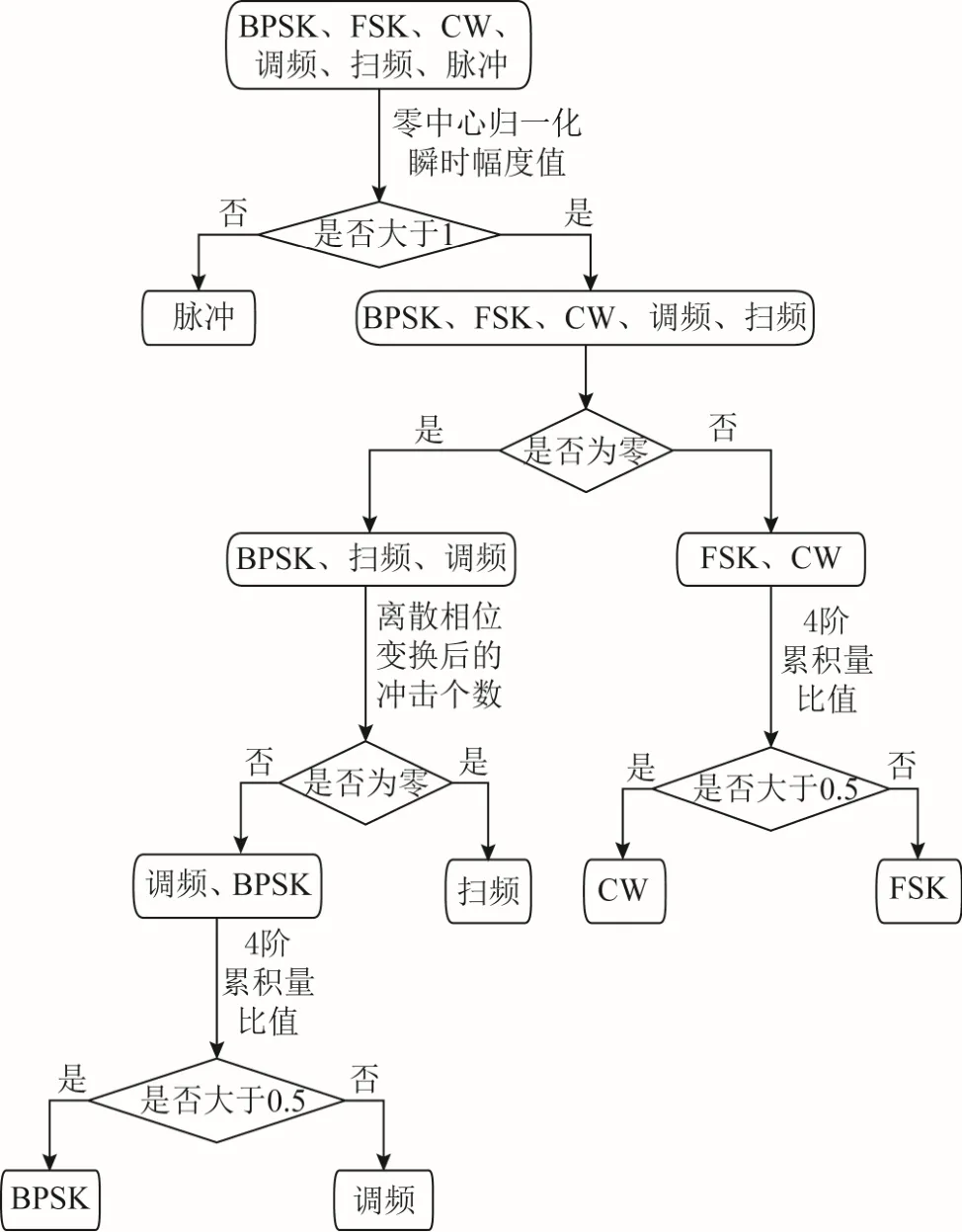
圖2 信號識別流程

2.1 干擾類型

本系統可以識別衛星導航系統所面臨的主要干擾類型，包括單頻干擾、脈沖干擾、線性掃頻干擾、調頻干擾、BPSK及FSK干擾。

單頻干擾的數學模型為

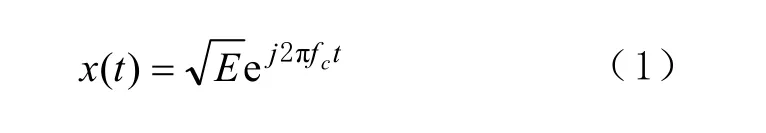
式中：fc為信號的載頻；E為信號功率；t為時間。脈沖干擾（pulse）的數學模型為

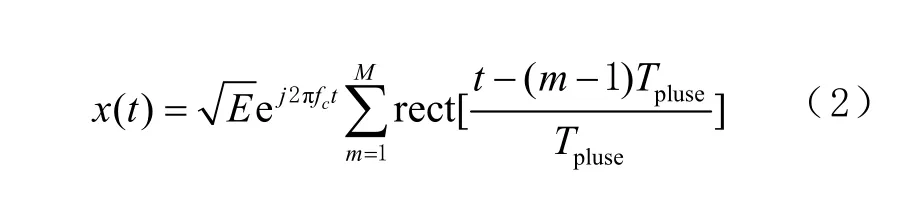
式中：M是信號的周期內高電平個數；Tpluse為脈沖周期；rect(t)為門函數。

掃頻干擾（sweep frequency，SW）的數學模型為

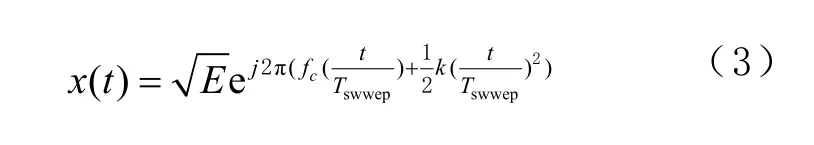
式中：Tsweep為掃頻周期；K為掃頻信號的頻率變化率。

BPSK干擾的數學模型為

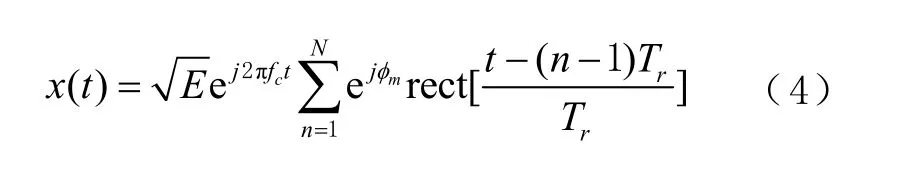
式中：Tr為碼元周期；m為進制數，為0、π；N為碼元個數。

調頻干擾（frequency modulation， FM）的數學模型為

式中：fm為調制信號的頻率；mf為調制指數。

FSK干擾的數學模型為

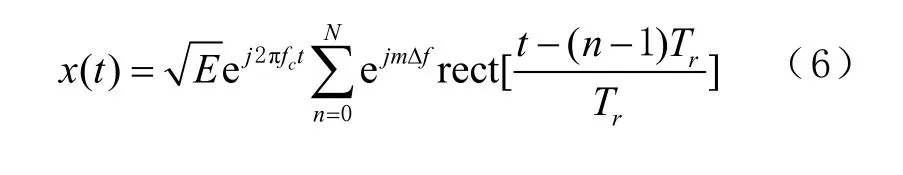
式中Δf為信號的頻偏。

2.2 信號的特征提取

不同類型的調制信號，具有不同的特征，下面將詳細研究如何利用調制信號的不同特征對信號進行特征提取，本文利用了時域、頻域以及統計域的特征。

2.2.1 零中心歸一化瞬時幅度譜密度的最大值

在 2.1節描述的信號中只有脈沖信號的瞬時幅度是變化的，其他調制信號的瞬時幅值是恒定值，因此可以利用幅度信息來將脈沖信號與其他調制信號區分。

為了減少噪聲以及個別離群值的影響，須提高識別方法的穩定性。首先，對瞬時幅度做零中心歸一化處理，再對處理后的信號做傅里葉變換。幅度恒定信號做零中心歸一化以后幅值在零附近波動，頻率遍布整個帶寬內，無明顯最值。脈沖信號的瞬時幅值隨著脈沖周期不斷的變化，其傅里葉變換后，在某個頻點處呈現出明顯的最值（如圖3所示）。因此可以利用

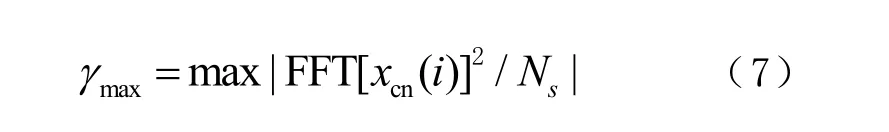
將脈沖信號識別出來。式（7）中：Ns為采樣點數；為零中心歸一化瞬時幅度。零中心歸一化過程為

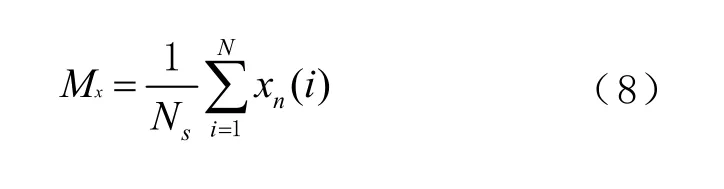
信號歸一化的表達式為

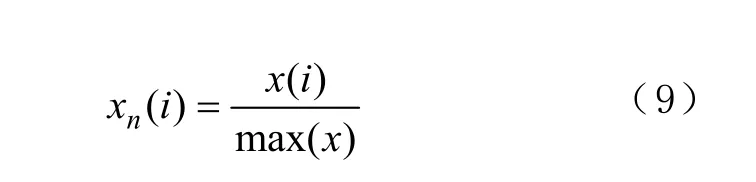
其中max(x)為信號的最大值。

信號的零中心化的表達式為

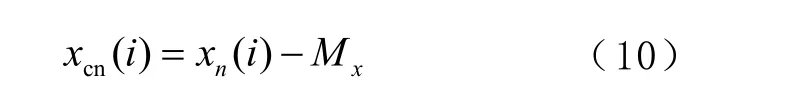
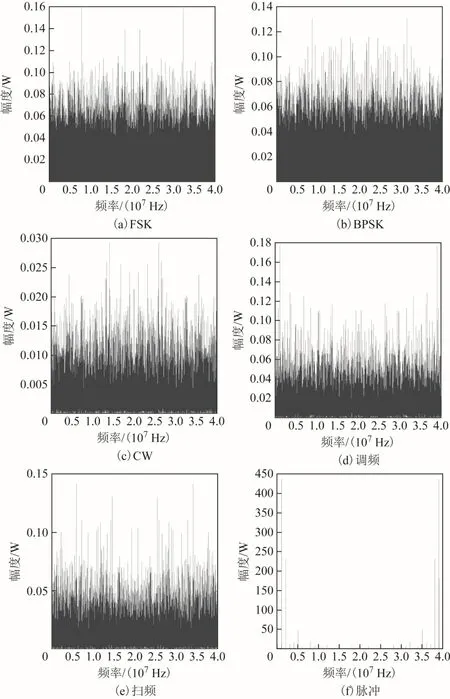
圖3 零中心歸一化瞬時幅度譜密度

2.2.2 沖擊個數1δ

不同的調制信號的功率譜計算公式為：

1）FSK

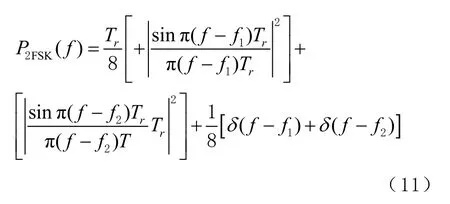
2）BPSK

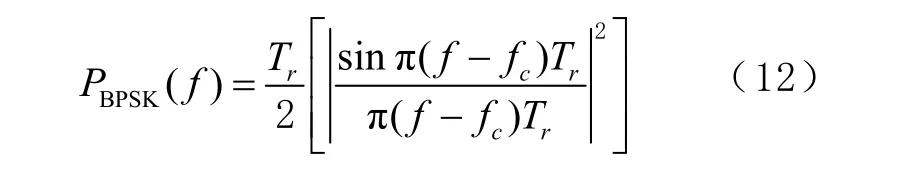
3）CW

4）脈沖

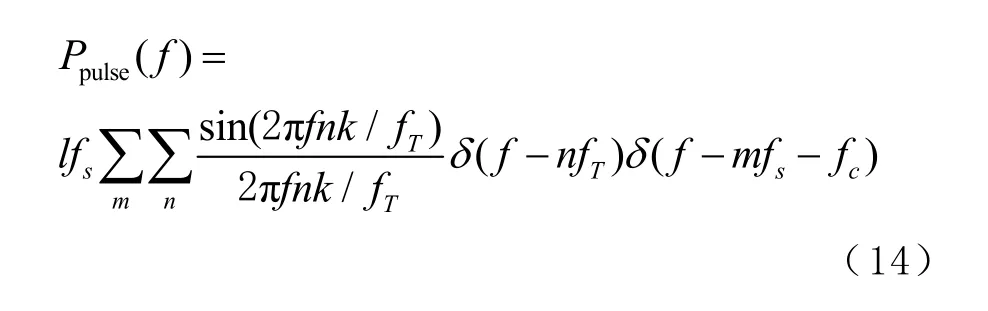
式中：fs為采樣率；fT為脈沖頻率；l為占空比。

5）調頻

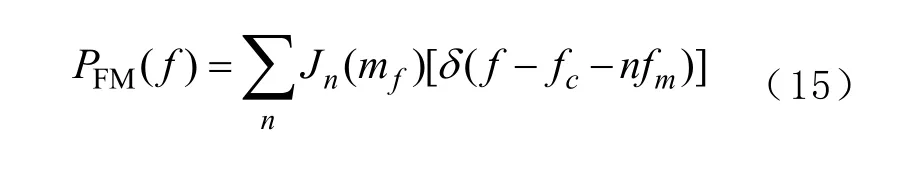
6）掃頻

式中K=B/Tsweep，B為帶寬。

從圖4的功率譜可以看出，FSK、CW的功率譜都有沖擊函數，而其他的調制類型的信號沒有，由此可以根據沖擊個數1δ將FSK、CW與其他類型的調制信號區分。

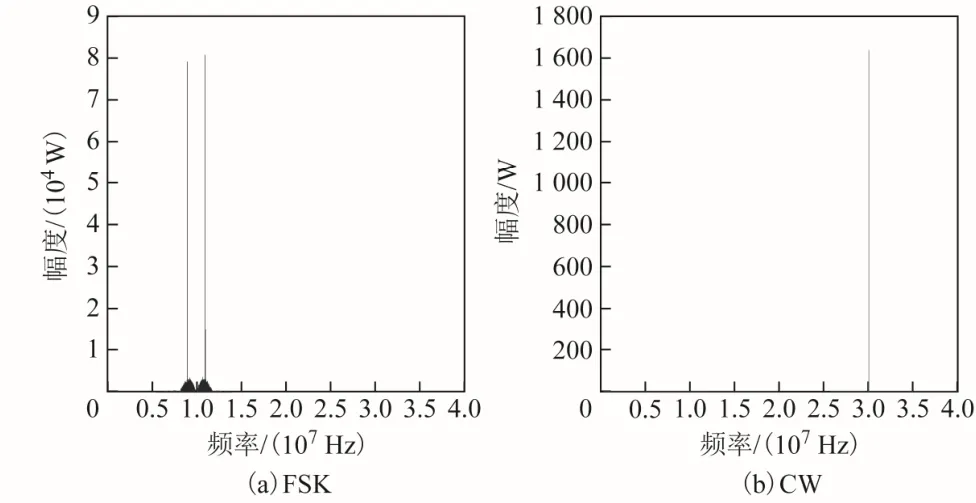
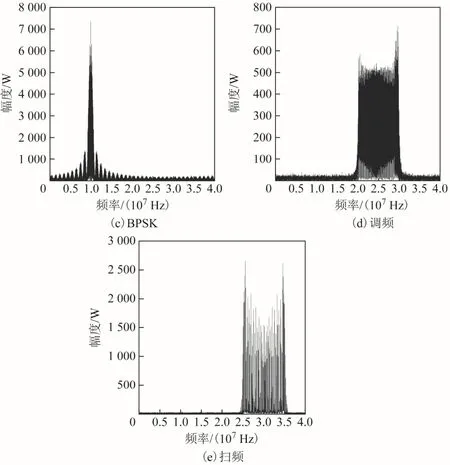
圖4 5種干擾信號的頻譜

2.2.3 沖擊個數δ2

由于線性調頻信號和單音余弦調頻信號頻率是不斷變化的，其在時域和頻域都沒有區分度，因此可以通過離散相位變換區分，離散相位變換定義為

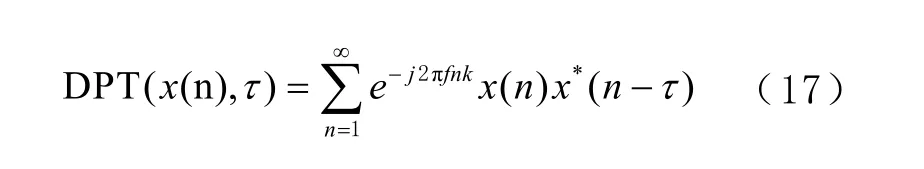
式中：τ為時間延遲；x*(n)為x(n)的共軛。根據離散相位變換的定義，可以得出線性掃頻信號的離散相位變換后的表達式為

根據式（18）可以得出離散相位變換后的掃頻信號為一個單頻信號。

調頻信號的離散相位變換后的表達式為

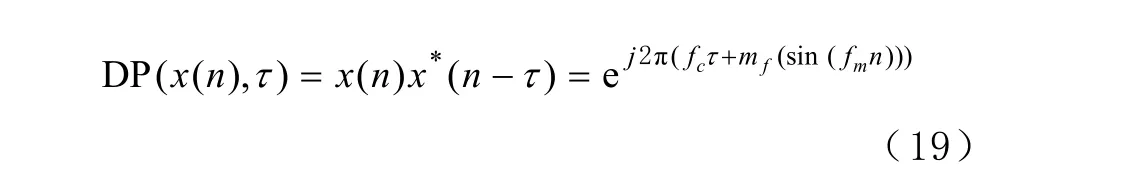
根據式（19）可以得出離散相位變換后的調頻信號仍然為一個具有帶寬的信號，即BPSK為

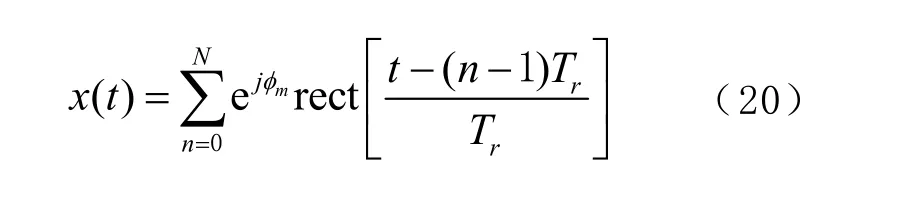
根據式（20）可以得出離散相位變換后的BPSK信號為基帶的碼元信號。

對離散相位變換后的信號做傅里葉變換后，掃頻信號含有沖擊函數，而BPSK和調頻信號沒有沖擊信號，由此可以將掃頻信號識別出來。

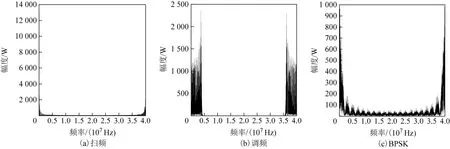
圖5 3種干擾信號離散相位變換后的頻譜

2.2.4 高階累積量

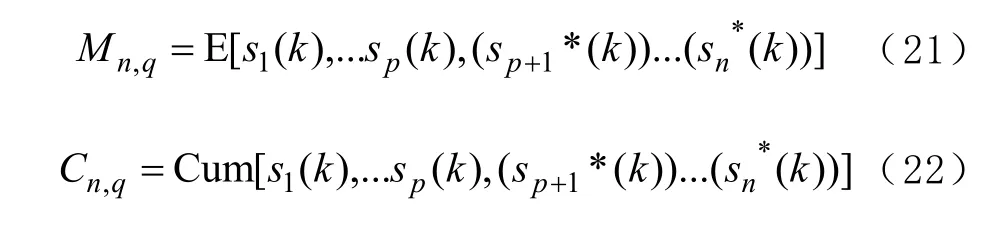
因此對于均值為零的平穩復基帶隨機過程，2階和4階累積量的表達式分別為

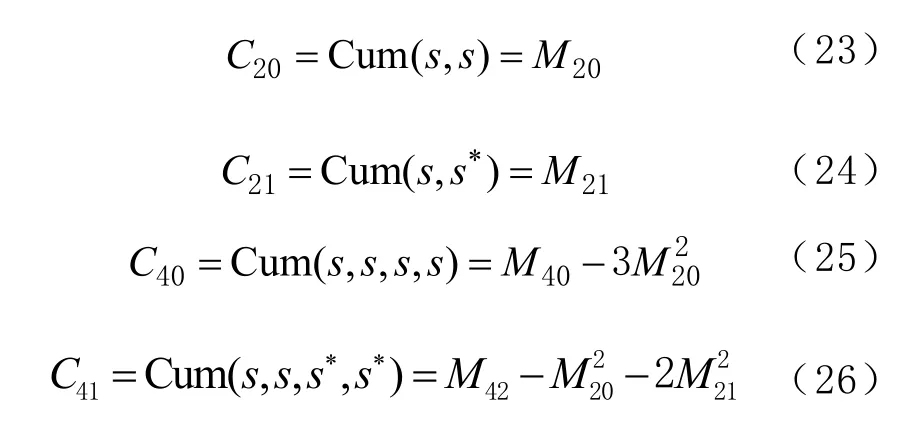
根據高階累積量的定義可以知道，對于實信號它反映的是不同調制信號其隨機變量的概率密度的分布情況，對于復信號它反映的是不同調制類型信號的星座圖的分布情況。并且對于不同的調制信號類型的高階累積量可能相同，但是不同的高階累積量的調制信號類型肯定不同。因此可以利用高階累積量來進行信號調整類型的識別。利用上述公式計算不同調制信號的高階累積量（如表 1所示）。令根據表格可以將單載波干擾和FSK區分開、調頻干擾和BPSK干擾區分開。

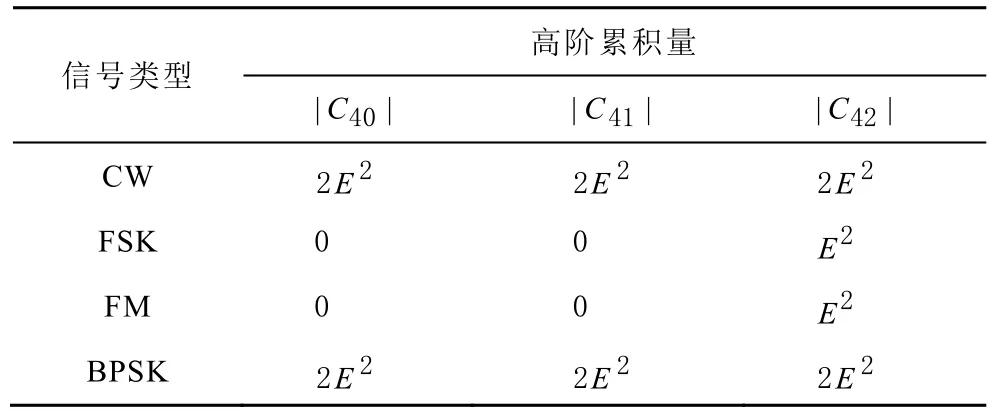
表1 高階累積理論值

2.3 參數估計

本文中主要估計干擾信號的載波和碼速率，并且估計了脈沖信號的周期和占空比。

2.3.1 載波估計

本文中利用頻域估計方法將信號變換到頻域，利用信號的對稱性估計信號的載頻。公式為

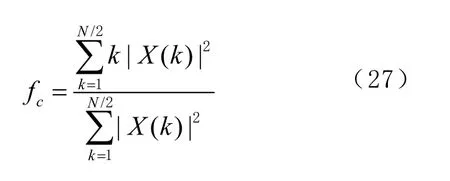
式中：X(k)為信號的傅里葉變換：N為傅里葉變換的點數。

2.3.2 碼速率估計

碼速率估計的精確與否直接關系到接收端定時序列的重構以及基帶信號的正確抽判，因此它也是信號估計的一個重要參數。本論文中利用小波變換的方法估計數字調制信號BPSK和FSK的碼速率。具體步驟如下：

以Haar函數作為母函數，對接收信號進行2次小波變換后，圖中可以看出BPSK和FSK只有在碼元變換的時刻有沖擊信號，而碼元周期內為常數值，接著對小波系數進行傅里葉變換，這樣就根據頻譜的最大值與次大值之間的頻率間隔得到碼元信號的頻率（如圖6、圖7所示）。

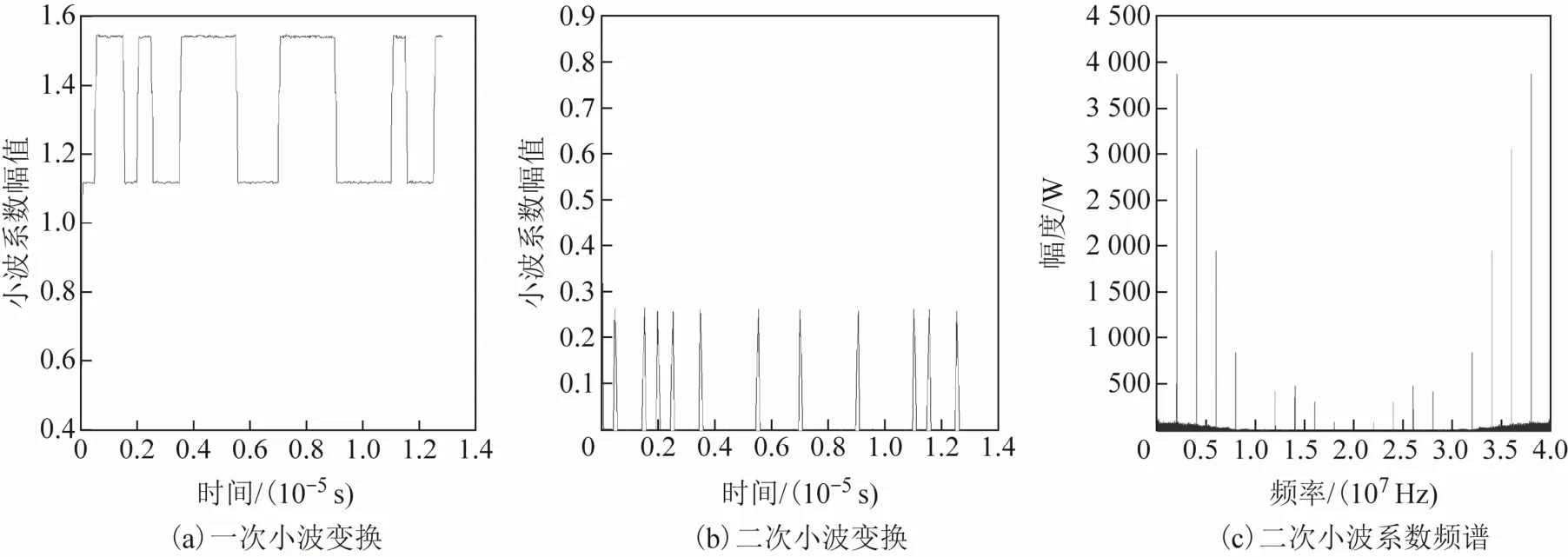
圖6 FSK的小波變換

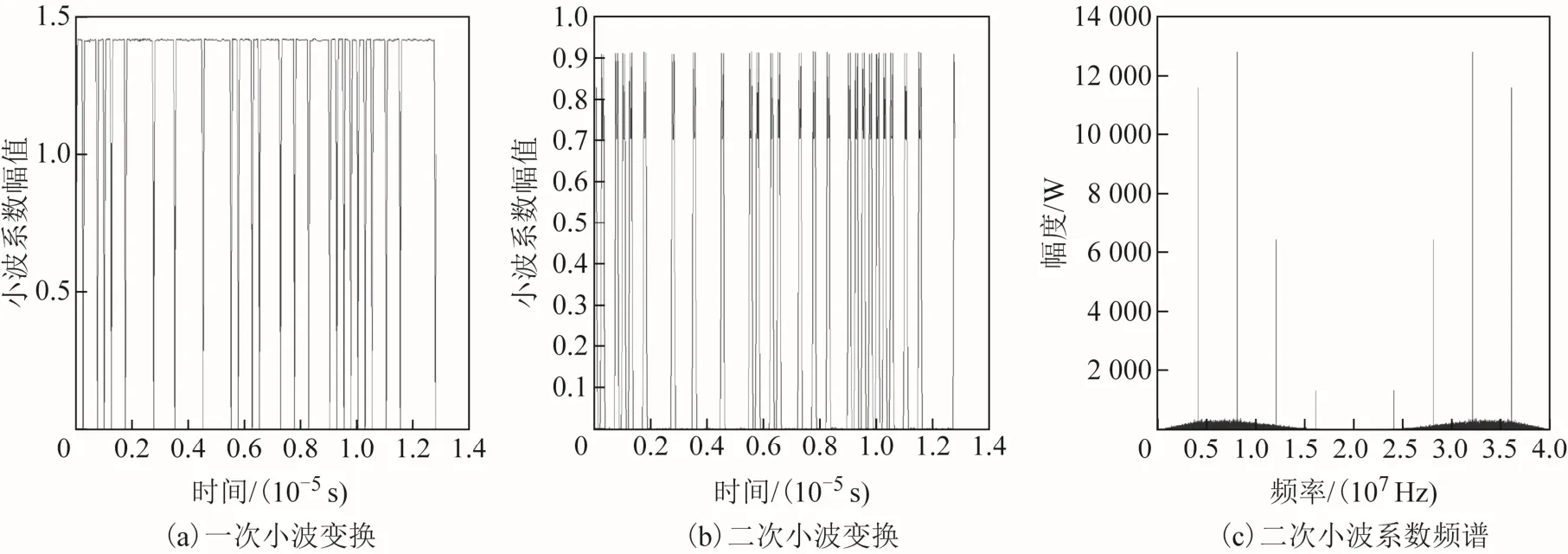
圖7 BPSK的小波變換

2.3.3 脈沖周期和占空比的估計

脈沖信號瞬時幅度如圖8所示。

1）估計信號的占空比。首先把信號下變頻到0、1電平的基帶信號，即對復信號求模值即可。其次，估計0、1電平的均值，求大于均值的點數，再用大于均值的點數除以總的點數，即占空比。

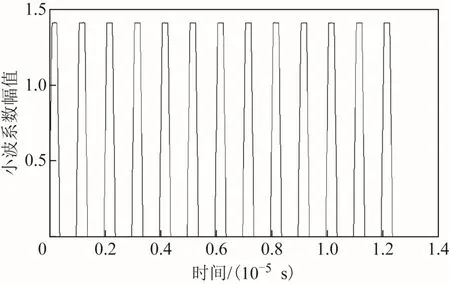
圖8 脈沖信號的瞬時幅度

2）估計信號的脈沖周期。估計信號的頻譜為

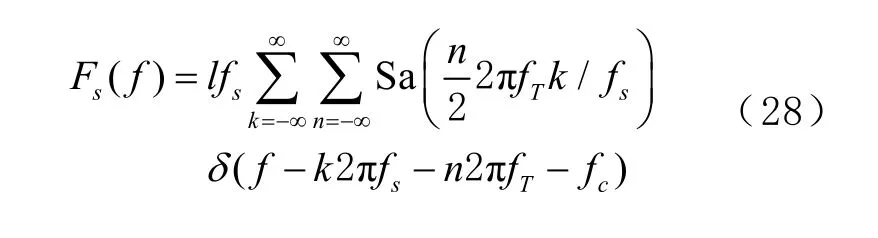
根據上式可以知道，頻譜的最大值和次大值的間隔為脈沖的頻率。

3 實驗與結果分析

典型的模式干擾盲識別系統主要由信號預處理、特征提取和分類判決3個部分組成，該過程的框圖如圖9所示。

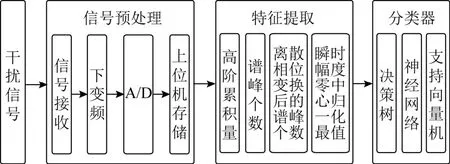
圖9 模式識別系統流程

3.1 仿真與結果實驗

1）實驗設置。為了驗證特征參數提取的有效性，實驗分別產生6種干擾信號，每種調制類型進行100次實驗，信噪比為20 dB，干擾信號調制參數如表2所示。

表2 6種仿真干擾信號參數設置

2）實驗結果與分析。根據以上的信號調制的參數設置估計出每個特征參數，取 10次實驗的平均值。實驗結果表明在以上信號調制參數設置下，以上5個特征參數完全識別6種調制類型的信號。特征估計參數如表3所示。

表3 6種仿真干擾信號特征參數

3）根據參數估計所用到的方法，對脈沖信號的占空比以及脈沖周期、BPSK和FSK的碼速率以及載頻進行參數估計（如表4所示）

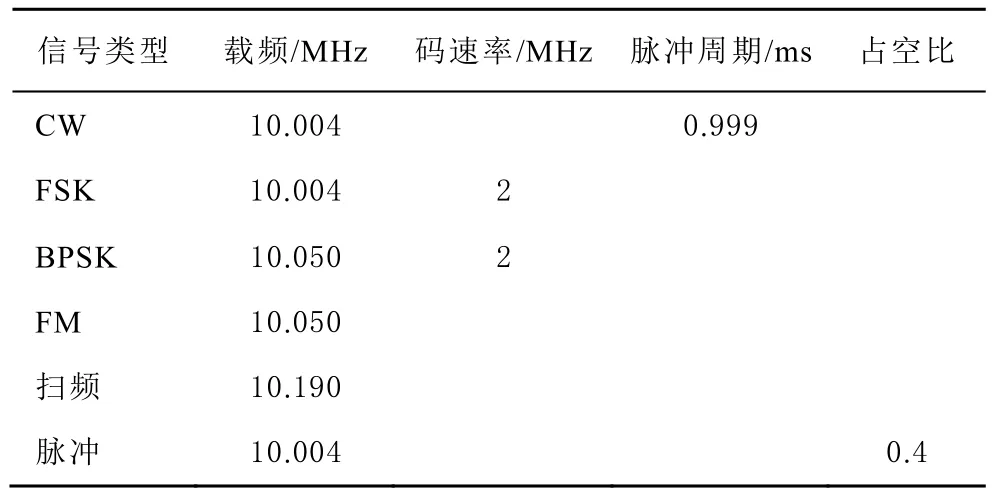
表4 3種干擾信號的參數估計

根據表格顯示的特征參數估計值與理論值相比較，這些特征參數可以對6種干擾信號進行分類。對干擾信號的調制參數的估計可以認為誤差都控制在1 %以內。

3.2 實測實驗

為測試上述方法的實際應用效果，在實驗環境中進行了測試。實驗設置如圖10所示，實驗的信號參數設置如表5、表6所示，實測實驗結果表明4個特征參數可以有效對信號進行分類。表 5、表 6分別是接收的實際信號所設置的參數以及所提取的特征參數。

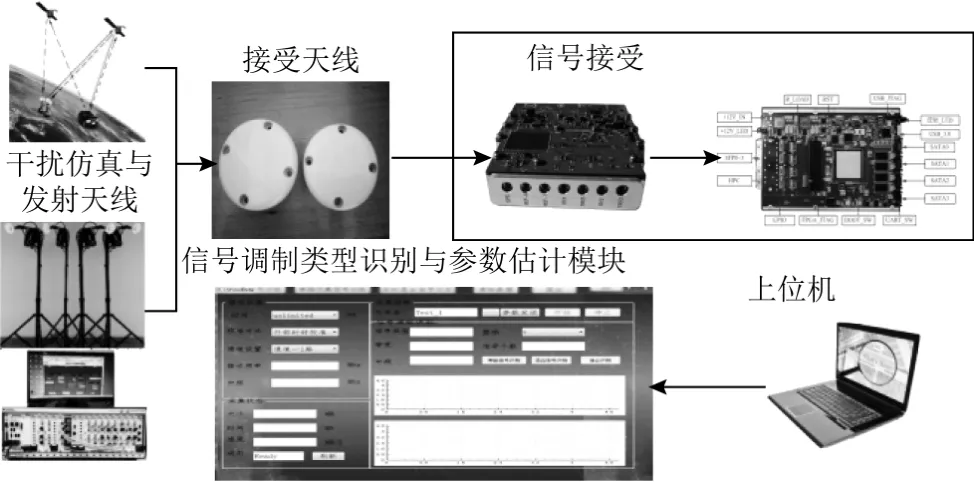
圖10 實驗硬件設置及軟件設置

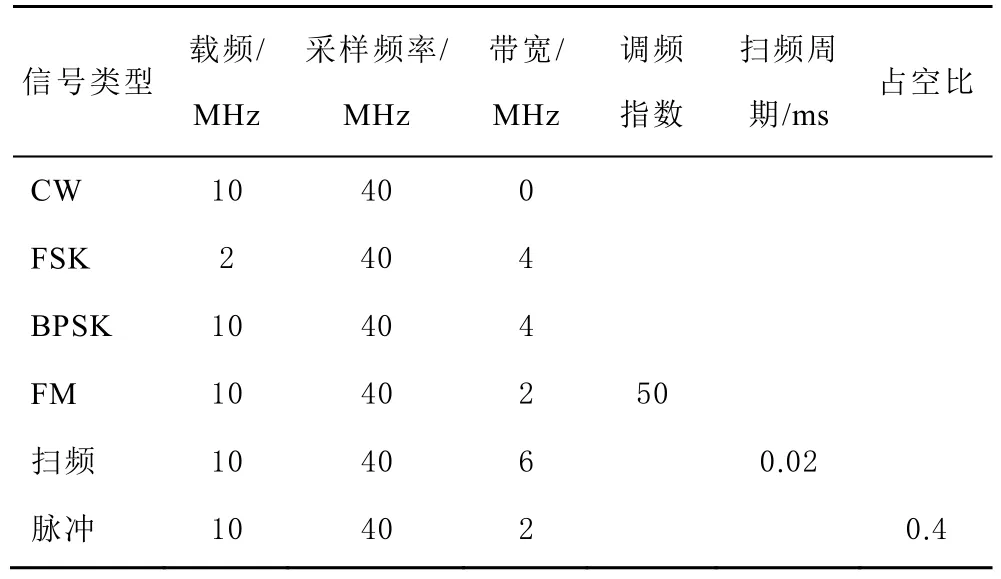
表5 6種實際接收干擾信號參數設置

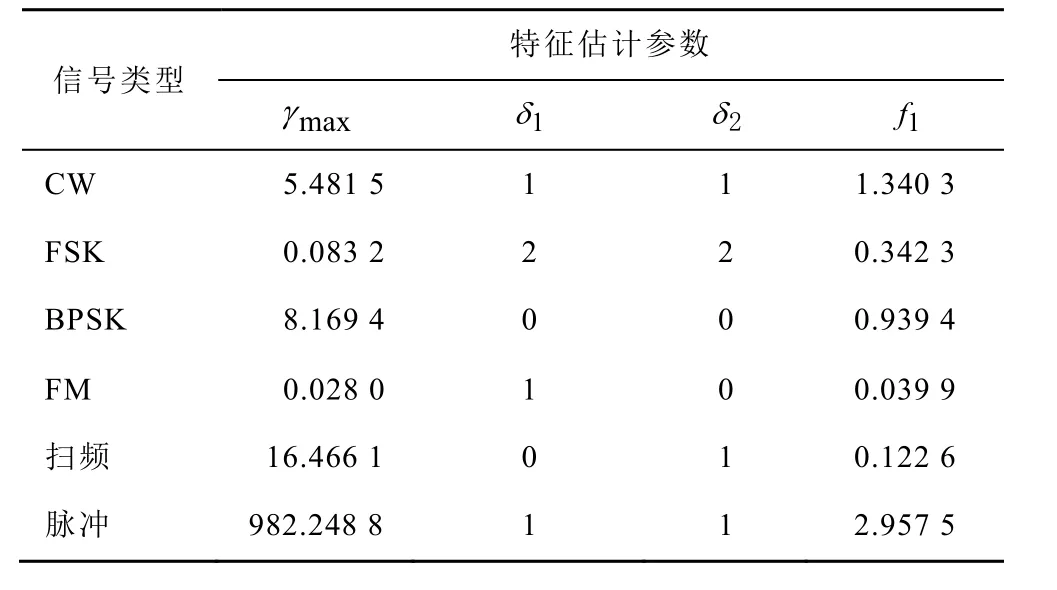
表6 6種信號的特征參數

4 結束語

由于導航干擾信號類型的多樣性，本論文在特征提取時也采用了多種方法，將高階累積量、譜分析以及離散相位變換相結合，得到5個特征參數：4階累積量的比值、譜峰個數、離散相位變換后的譜峰個數、瞬時幅度零中心歸一化的最大值。實現6種導航干擾信號的分類。在仿真實驗中也證明了混合識別算法可以有效地識別數字調制信號與模擬調制信號的6種干擾信號；最后利用實驗室現有的信號采集設備進行驗證，具有較好的工程實用價值。