邊緣檢測和證據理論在機器人目標識別中的應用

王 凱， 夏國廷， 李立偉， 蘭 勇， 馮 曉

(青島大學自動化與電氣工程學院，山東青島266071)

0 引言

近年來，人工智能的發展成為科技前沿的熱門研究領域。仿生機器人作為機器人領域中的最先進的代表，融合了傳感技術、信息傳輸、自動化控制等多學科的知識，成為了研究最為廣泛的一類機器人。NAO機器人作為世界上最熱門的仿人智能機器人，廣泛應用于人們的生活中［1-5］。

NAO機器人具有25個自由度，并在不同的部位配有相應的傳感器，該機器人的視覺開發是一個非常熱門的研究方面。NAO機器人主要靠視覺系統來感知周圍的環境，首先采集相應的圖像，然后結合HSI顏色空間的邊緣檢測進行圖像的預處理。除去圖像噪點，得到較優化的圖像，然后再對目標物體進行顏色的辨別。

對于機器人的不精確環境下的顏色識別問題，已有人工智能(AI)、模糊系統(FS)、遺傳算法(GA)和神經網絡(NN)方法來解決。對于實時移動的機器人，FS方法被認為是效率和精度最高的方法。一般的顏色識別方法基本思想是構造隸屬函數，以確定HSI三維顏色空間的定義程度，然后使用Mamdani推斷來計算檢測到的輸出顏色［6-11］。

本文為了克服由于最小/最大算子涉及到的非線性問題，主要采用了HSI空間下的Takagi-Sugeno Fuzzy System with Constant Conclusions(TSCC)系統。在一個決策不精確的環境下進行雙攝像頭的目標顏色標定，與上述檢測到的目標邊緣信息融合，實現模糊系統下有色目標的識別［12-14］。

1 邊緣處理

邊緣處理是是整個圖像處理中最基礎也是非常重要的環節，它是后續圖像處理的數據源，提供了高效準確的原始圖像。圖像處理包含兩個方面，首先通過HSI顏色空間對原始圖像進行色彩分割;然后對色彩分割圖像進行離散小波濾波處理;最后對圖像進行邊緣檢測。

1.1 HSI顏色空間

通常色彩空間有 RGB、CMY、YUV、HSV、HSI等。為了更好地對圖像進行數字化處理，進一步提高識別效果，本文采用了HSI顏色空間進行圖像的預處理。

HSI顏色空間是一種均勻的顏色空間，色彩空間的距離與坐標點上的歐幾里德距離成正比(見圖1)。HSI顏色空間具有以下優點:當采用RGB顏色空間時，改變其中某一顏色的屬性，比如改變色度就必須同時改變R、G、B 3個坐標。因為HSI空間中的3個坐標式是獨立存在的，當采用HSI坐標空間時，只需要改變H坐標。

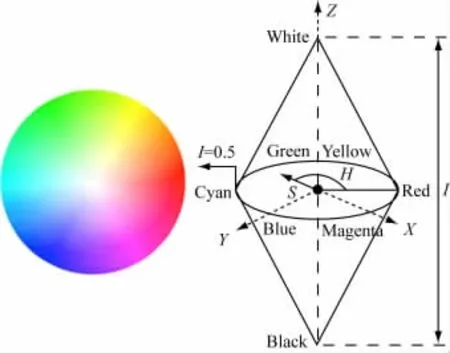
圖1 HSI圓錐空間模型

在NAO機器人中，彩色圖像都采用RGB模式，因此，需要進行顏色空間的轉換。RGB模式到HSI模式的常用轉換公式如下:

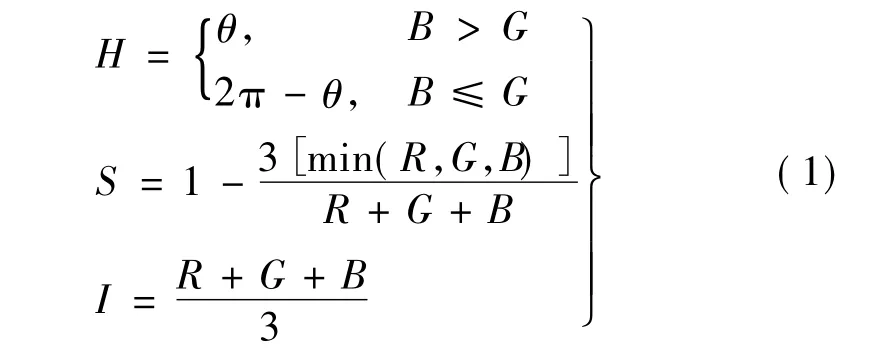
式中:

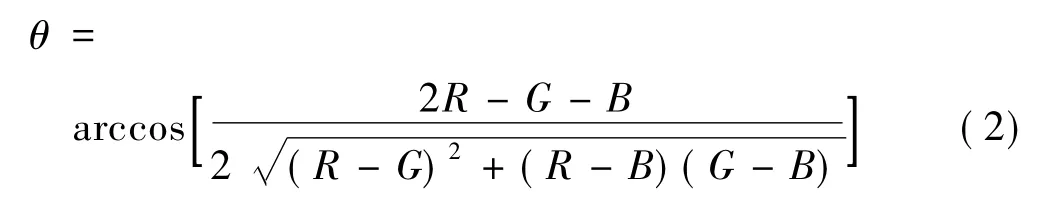
利用RGB-HSI模式轉換原理，將RGB顏色空間下的圖像進行轉換。

如圖2所示，(a)為RGB顏色空間下的原圖，(b)為HSI顏色空間下的H通道示意圖，(c)為HSI顏色空間下的S通道示意圖，(d)為HSI空間下的I通道示意圖。HSI顏色空間對R、G、B 3個分量重新編碼，其中，色度分量在［0，2π］的范圍內;飽和度分量和亮度分量在［0，1］的范圍內。HSI空間有兩個重要特點:亮度分量H與圖像的彩色信息無關，色度分量S、飽和度分量I與人感知彩色的方式緊密相關。

圖2 RGB轉HSI示意圖

由于從RGB顏色空間到HSI顏色空間的轉換是非線性的，對圖像的噪聲較為敏感，因此采用離散小波變換對圖像進行平滑去噪，即分別對R、G、B分量進行濾波處理。

1.2 離散小波變換去噪處理

本文利用離散小波變換(Discrete Wavelet Transform，DWT)進行圖像的去噪處理，避免了由于連續小波變換導致的較大的計算量。使用濾波器進行離散小波變換的示意圖如圖3所示。圖中:S代表的是原始信號，通過高通濾波器與低通濾波器產生了A與D信號;A信號表示的是原始信號的近似值;D信號表示的是原始信號的細節值。實現離散小波變換，將內部尺度因子與平移因子進行了適當的離散化。在圖像處理中，噪聲大多存在于高頻部分，通過小波變換可對圖像進行有效的降噪處理。

圖3 離散小波變換示意圖

1.3 HSI邊緣檢測

在對數字圖像進行邊緣檢測時，有幾種常用的邊緣檢測算子:梯度算子、Roberts邊緣檢測算子、Sobel邊緣檢測算子、Prewitt邊緣檢測算子、Laplacian邊緣檢測算子等。但實際應用中，Canny算子不止是簡單地通過計算圖像的梯度信息檢測邊緣，而是通過鄰域像素點的特點進行邊緣的尋找和連接，這樣就可以獲得更加完整的邊緣。

本文提出在HSI顏色空間中采用離散小波變換Canny算子邊緣檢測的方式對圖像進行處理，通過最大熵決策機制提取梯度信息，融合多方向的邊緣信息。用一結構元素作為“探針”探測融合的圖像邊緣信息，保留與結構元素相匹配的結構，抑制正負脈沖噪聲，保持細節和邊緣。圖像識別流程可簡單描述如圖4所示。

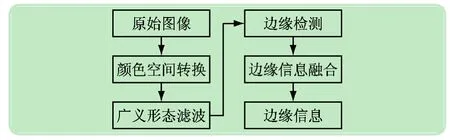
圖4 HSI邊緣識別流程圖

Canny算子具有較好的檢測性能和比較高的定位精度，并且邊緣響應次數較少，可以實現單像素邊緣的檢測，而且不會受噪聲的影響產生偽邊緣。圖5所示為離散小波變換下的可自動適應閾值Canny算子得到的示意圖。

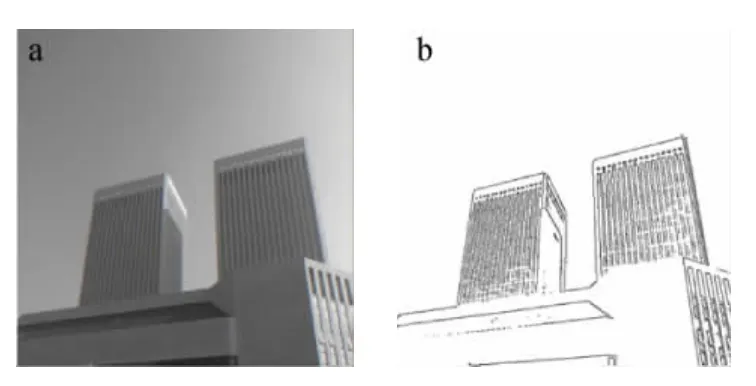
圖5 Canny算子示意圖

Roberts邊緣檢測算子只用了相近的4個點的灰度值進行邊緣的計算，所以該算子可以實現精確的定位并且計算量很小，但是對噪聲比較敏感。Prewitt算子通過計算鄰域內像素點之間的差值進行邊緣的檢測，由于邊緣部分得到的計算數值比較大，可以利用這個優勢消除一部分的虛假邊緣，對于噪聲有一定的平滑能力，具有降噪的效果，如圖6、7所示。

圖6 Robert算子

對經過Canny算子得到的圖像進行非極大值抑制，即對邊緣進行細化處理。通過比較鄰域內的梯度幅值，保留了梯度變化最為劇烈的位置達到精確定位的目的，如圖8所示。

圖7 Prewitt算子

圖8 對像素進行非極大值抑制示意圖

設f(x)為定義在二維離散空間上的離散函數，結構元素g1(x)和g2(x)為Z2上的有限子集，則廣義形態開(GO)和廣義形態閉(GC)濾波器分別為:

圖像的像素進行非極大值抑制之后，對圖像的點φ(x，y)進行雙閾值標定，即對邊緣色度進行帶狀區域M識別，在閾值范圍之內的像素點標定為

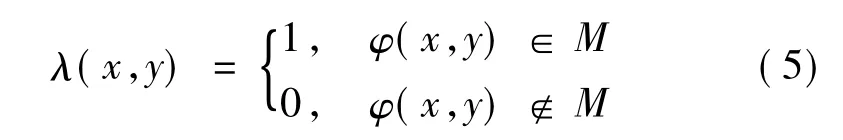
采用雙閾值法對邊緣點進行像素點的標定，給邊緣點留有一定的裕量，提高了目標識別的準確性和邊緣的容錯性，使得目標輪廓無限逼近真實目標。圖9為NAO機器人HSI空間下經過非極大值限制和雙閾值法進行處理的的目標識別示意圖。

圖9 目標邊緣檢測

2 雙攝像頭顏色識別系統

通常，目標的不確定性的主要原因之一是源于它的不精確性。事實上，識別信息的不精確性會增強決策的不確定性。同樣地，利用信息的不確定性也會導致其處理序列的不精確性，通常這兩個缺陷是相關的。

為了改善以上缺陷，本文構建了雙攝像頭融合的系統。圖10顯示了該架構的結構開發方法，它的運行是基于模糊系統中的證據理論。單一攝像頭色彩識別容易受不確定因素(例如:光照，動態目標移動，容錯誤差等)影響，導致識別精度下降。假定有n個攝像機可供觀察目標，這些輸出值被傳送到融合機制做出顏色判定［15］。

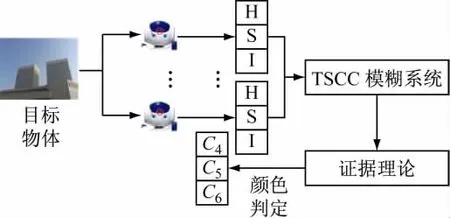
圖10 多攝像頭顏色識別流程

2.1 模糊系統

設Ω是一個有限的非空集合，包含顏色識別問題中所有可能的決策。P=2Ω是所有可能的子集組成的源集，Ω和P分別為:

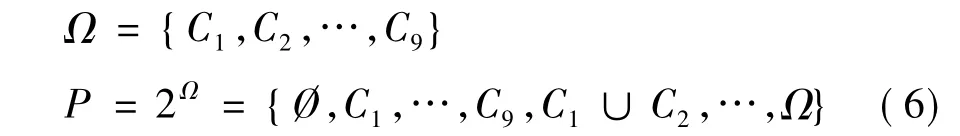
證據理論始于使用基本概率分配(BPA)在Ω中表示證據的程度的思想，BPA中的m是一個從P到［0，1］對源集中的每個元素標定可靠度的映射，具有以下屬性:

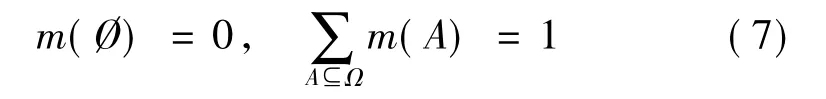
空集的0值代表完全不相信假設;1代表完全相信。ω的值表示為m(Ω)，代表不確定的數量，具有非空集的子集稱為焦點元素。在此背景下，系統的輸出，即尋求顏色Ci的結果必然是一個包含所有可能的集合:

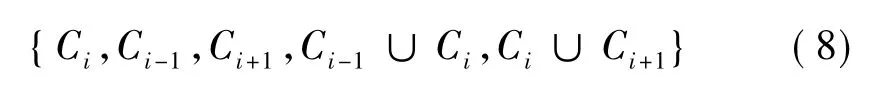
沖突情況不代表被丟棄，可以認為是在選擇閾值時，對顏色的標定是不確定的。為了減少目標搜尋的時間復雜度，對每種顏色Ci的辨別空間Ωi定義如下:

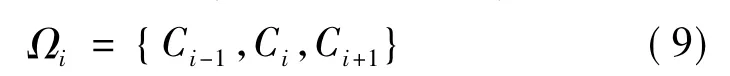
Ωi中包含所有可能的子集的源集空間由Pi提供:

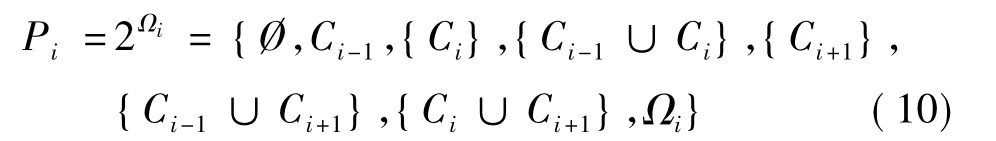
模糊化方法在于將一個清晰的目標值作為模糊系統的輸入。如圖11所示嚴格劃分識別空間，建構具有三角形和梯形隸屬函數。在該框架中，給每個子集分配模糊的隸屬函數。因此，系統提供的輸出是在可能的識別空間子集上模糊化。根據這一原則，與TSCC系統相關的值向量的模糊輸出被構造出來。在這種情況下，對于顏色C的矢量值m(C)由下式給出:

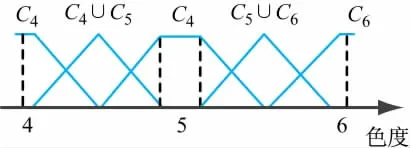
圖11 模糊系統下的色度分布

2.2 顏色識別

基于以上理論，本文使用NAO機器人頭部的上下兩個攝像頭進行驗證所述的融合方法，通過兩臺攝像機識別目標建筑的顏色。

根據表1，棕色的數字是5(C5)。在檢測過程中，兩臺攝像機捕捉同一個對象但給出不同的結果，即Out1=5.85和Out2=4.45。但是，兩者的結果卻處于沖突狀態(相機之間分別猶豫不決{紅色(C4)，棕色(C5)}和{棕色(C5)，黃色(C6)}之間。在這個例子中，Out1=5.85(與相機1有關)是更接近黃色，但它不是黃色(因為這個值在褐色的區間檢測之外，即5.85［5.9，6.1］)。在這種情況下，識別系統(模糊系統)猶豫在紅色和棕色之間。換句話說，顏色可以是紅色或棕色。同樣的標定在攝像機2中作出Out2=4.45，引起沖突棕色和紅色之間的情況(顏色可以是棕色或紅色)。在這個框架中，一些關于棕色的庫顏色存儲在沖突的替代顏色中:{紅色，棕色}和{棕色，黃色}。證據理論的目的是解決這些出現的沖突問題，以便更精準地做出相關顏色的標定。

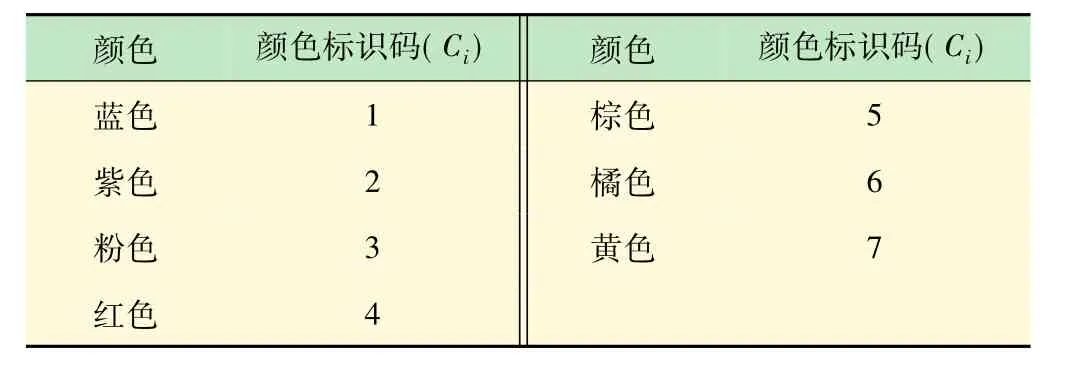
表1 顏色標識碼

如果待檢測目標物體被認為是可靠的，基于距離的算法也被使用，那么檢測到的顏色肯定會是棕色。如圖11所示，棕色是距離最近的，到相對于相機1的輸出。然而目標源只有部分可靠，而基于距離的算法則不能給出連貫可靠的結果。在這種情況下，初始的證據理論可以作為一個可替代方案，因為在解決沖突的決策進程中證據理論具有提取有用信息和整合可靠性的能力。

在此例證的背景下，減少的辨別空間是Ω5={C4，C5，C6}和包含所有可能的功率集合空間的子集:

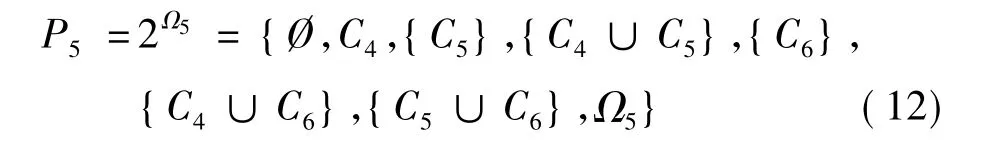
根據圖11能夠從中得到模糊系統下的色度分布情況。事實上，表2顯示了單攝像機系統下的m1和m2兩個攝像頭沒有可靠性。在加權之前，模糊系統的m1和m2之間的沖突等于0.802。這里需要注意的是，來自不同的證據源(攝像頭)在精確的環境下可能會得到不完全可靠的信息。

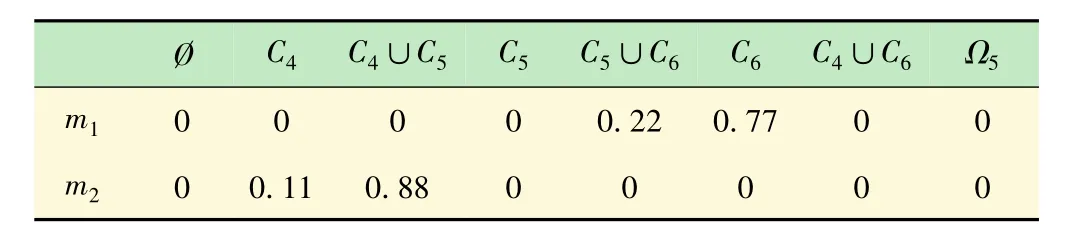
表2 單攝像機系統下的顏色識別

因此，在融合過程中必須考慮證據源的可靠性，如果這些源可靠性較好，可以給定它們一定的權值來表征影響。在本算法中，假定攝像機m1的可靠度α1=0.7，攝像機m2的可靠度α2=0.6。對于每個證據源，加權方法都會乘以可靠性因素。因此，可靠度改變了每個來源的權值以反映其信譽，從而改善決策過程。表3顯示了相機可靠性 α1=0.6、α2=0.7。系統中m1和m2之間的沖突k=0.337意味著兩個來源之間的合理沖突加權之后的可靠性被削弱。使用Dempster-Shafer(DS)規則和最大pignistic概率給出的決定如表3所示，從中可以看出，融合后的決定是棕色C5。所以機器人可以識別目標對象并據此做出決策。

表3 融合后的顏色識別決策

考慮單攝像頭、雙攝像頭系統分別識別有色目標，其中雙攝像頭系統采用的是所述模糊系統證據理論方法。識別性能結果如表4所示。

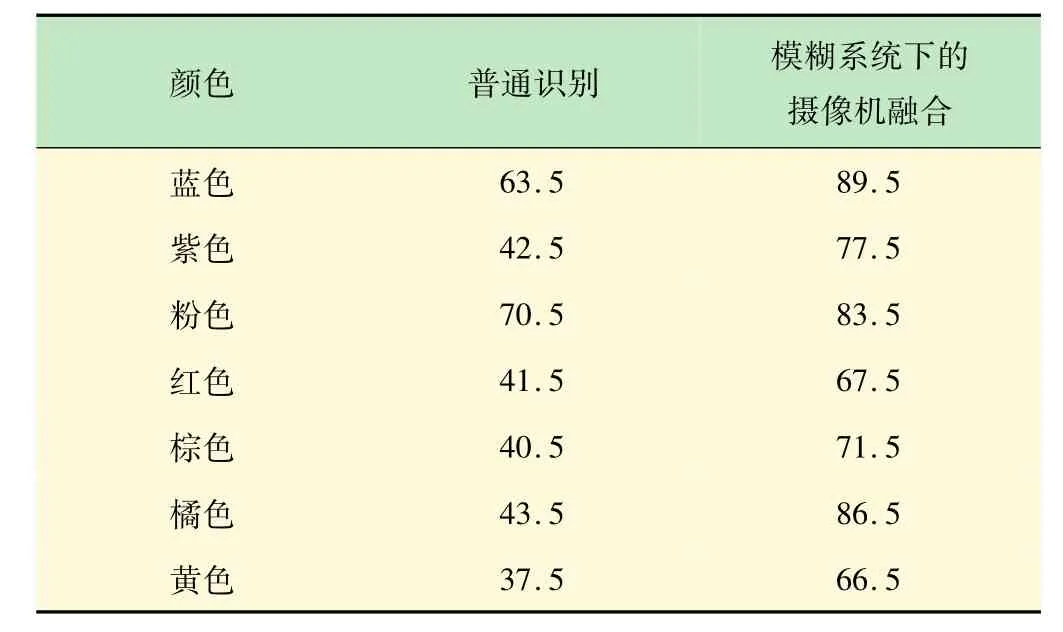
表4 顏色識別性能 %

在HSI顏色空間中，模糊系統下的雙攝像頭系統識別質量和精度要提高約29%，經計算融合過程的執行時間為0.37 s，保證了目標識別的實時性。

3 結語

本文采用基于HSI顏色空間的離散小波變換方式，利用可自動適應閾值Canny算子邊緣檢測方法和雙閾值法提高了圖像邊緣的準確性和容錯性，使得目標輪廓無限逼近真實目標。通過基于TSCC系統下的證據理論融合與決策機制對NAO機器人雙攝像頭系統進行圖像的顏色標定，將目標圖像的識別性能提高了約29%。本研究未來將著重于將這種方法擴展到3D彩色域，使用模糊和漸變的相機進行動態多元目標識別。