基于逐步回歸法的BP神經網絡在大壩滲流分析中的應用

謝文群

（江西省大余縣水庫工程管理局，江西 大余 341500）

大壩安全監測資料分析方法常用統計模型、確定性模型和混合模型[1]等，這些模型均建立在數理統計的基礎上，影響因子的選擇是模型精度關鍵之一，根據不同影響因素的確定方法，統計模型又可劃分為逐步回歸法、差值回歸法，正交多項式回歸法等，不同方法所建立的計算矩陣帶寬不同，計算速率及精度也有較大差異。

人工神經網絡模型是基于模仿生物大腦的結構和功能，采用數學和物理方法構成的一種信息處理系統或計算，由于具有非線性映射、分類和聚類、優化計算等特點，被廣泛用來解決不同種類數據之間的復雜關系，根據網絡結構的不同，神經網絡又可劃分為誤差反向傳播神經網絡（BP模型）、Hopfield神經網絡、Boltzmann機等[2]，仲云飛等[3]提出了利用遺傳算法優化BP神經網絡進行大壩揚壓力預測，張國翊等[4]提出了變更傳遞函數傾斜以和動態調節不同學習速率的BP改進算法，提高了缺陷識別率。繆新穎[5]等人則基于LM-BP神經網絡進行了大壩變形預測分析，在精度和訓練速上得到了提高。

1 逐步回歸模型

逐步回歸分析方法基本思想是根據自變量對因變量的影響顯著程度，將個因子逐步引入回歸方程中，依據重要性，有選擇性的剔除次要因子，直到顯著因子全包括在回歸方程以內為止，建立相對較為稀疏的計算矩陣，減小帶寬，提高計算速率；另一方面，更直觀了解影響因素，逐步分析法在進行異常原因分析，分析變化規律和發展趨勢等方面發揮重大作用。如傅蜀燕等[1]確定了大壩變形主要原因，其表明計算量少、精度高等；陳蘭等[2]利用逐步回歸法較好的分析了邊坡變形的變化規律和發展趨勢。本文采用逐步回歸法，結合某水庫大壩測壓管水位實測數據進行分析，為了解該水庫滲流運行狀態提供理論依據。

進行大壩滲流監測數據分析，首先需確定所有可能的影響因子，根據文獻[1]可知，大壩滲流影響因素可能包括水位分量f（H），降雨分量R及時效分量。由于滯后效應，水位分量H包括當日庫水位、前期庫水位、壩基水位、下游水位等，降雨分量包括當時降雨量及前期降雨量，時效分量主要為筑壩土體結構的固結對滲流影響。

2 BP神經網絡

2.1 標準BP神經網絡

誤差反向傳播(Error Back Propagation，BP)學習算法具有無反饋的神經網絡結構，采用有指導學習方式進行訓練和學習，通過比較輸出層各個神經元的實際輸出與期望輸出，獲得二者之間的誤差，按誤差函數按梯度方向，調整各個連續權值，達到減少誤差效果。

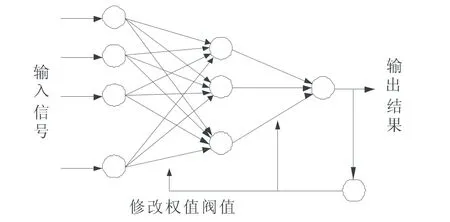
圖1 典型三層BP神經網絡結構圖

正向傳播：傳遞函數采用S型，按式(1)，將前一層作為輸

入，得出的輸出結果作為下一層輸入，直至求得最終輸出結果。

根據給定的期望輸出，求出與實際輸出的偏差為δtk：

其偏差期望為：

為使隨著連接權值調整按梯度下降，按照誤差按梯度下降原則，則有：

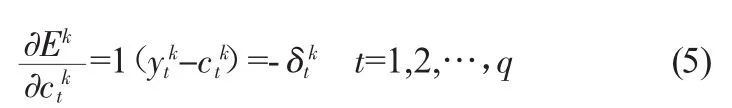
因此，隱含層至輸出層的連接權值V調整值為：

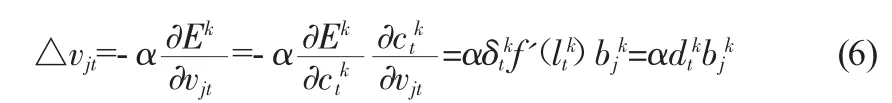
同理，連接權值w調整值為：

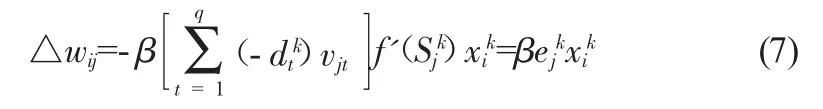
2.2 逐步回歸-BP神經網絡優化算法模型

由于標準BP網絡的算法在最速下降法存在缺點，如學習算法的收劍速度慢、存在局部極小點、隱含層層數及節點數選取缺乏理論指導，訓練時學習新樣本有遺忘舊樣本的趨勢[6]。為此，可從兩方面就進行改善，一方面引入動量因子、變學習速率等，另一方面采用更有效的數值優化方法，如共軛梯度學習算法、Levenberg-Marquardt算法及B&B算法等，不同的數值優化方法優缺點也差異明顯，Levenberg-Marquardt算法是應用于訓練BP網絡問題的牛頓算法的一個簡單版本，其突出優點是收斂速度快，而且收斂誤差小[7]。

另外，網絡結構的復雜程度，直接影響神經網絡訓練效率。當網絡層次及輸入變量節點越多，其計算精度可能越高，但迭代矩陣明顯加大，其訓練速度越慢，逐步回歸-BP神經網絡優化算法模型（以下簡稱混合模型）的思路就是在一定的精度下，首先通過逐步回歸法，確定顯著性影響因子，減少輸入層變量，達到簡化網絡結構，提高計算效率的效果。

3 實例分析

油羅口水庫位于江西省大余縣，正常高水位220.00 m，最大壩高36.3 m，為大(2)型水庫。主壩為混凝土心墻壩，大壩滲流設3個斷面，共14個測壓管，采用自動觀測監測壩體滲流。選取典型樁號0+144斷面，編號依上游往下游分別為UP401、UP402、UP403，其布置見圖2，記錄時間為2014年1月～2016年12月。

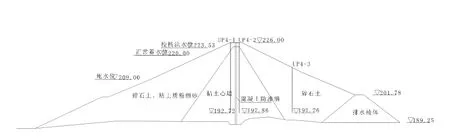
圖2 壩體測壓管典型斷面圖

3.1 影響因子分析

綜上，水位分量包括上、下游水位差及滯后時間，因此，選取當日至前7日各日上游水位作為影響因素；降雨主要是通過影響上游水位，而間接影響管水位，其過程較為緩慢，但若測壓管埋設質量不好，降雨入滲作用明顯，也會直接影響管水位，表現為管水位異常升降；時效分量主要由于土體固結沉降作用導致土體的滲透性發生變化；溫度因子對土石壩影響較小，可忽略。

分析表明，UP401管水位顯著性影響因子為H0及H1，UP402及UP403管水位顯著性影響因子均為H1與H3，其中，Hi為i天前的上游水位，降雨及時效等因子均為不顯著，計算時可忽略。

3.2 成果分析

采用MATLAB編程，分別進行逐步回歸、優化后BP神經網絡及混合模型的計算，其中，優化后BP神經網絡輸入變量采用所有可能影響因子進行分析，混合神經網絡(簡稱混合模型)采用顯著性影響因子作為輸入變量，其計算結果如下，圖3～圖5為三種模型擬合值過程線，表1～表3為計算結果擬合精度。

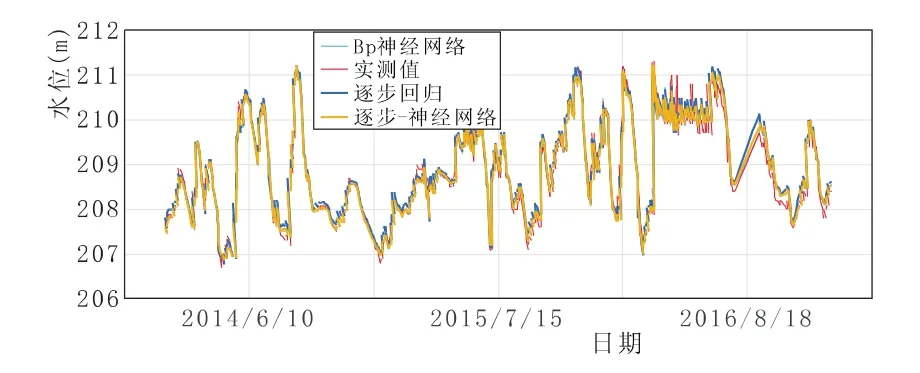
圖3 UP401測壓管實測水位與回歸值過程線

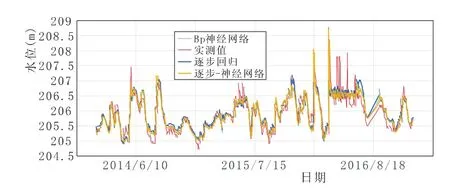
圖4 UP402測壓管實測水位與回歸值過程線

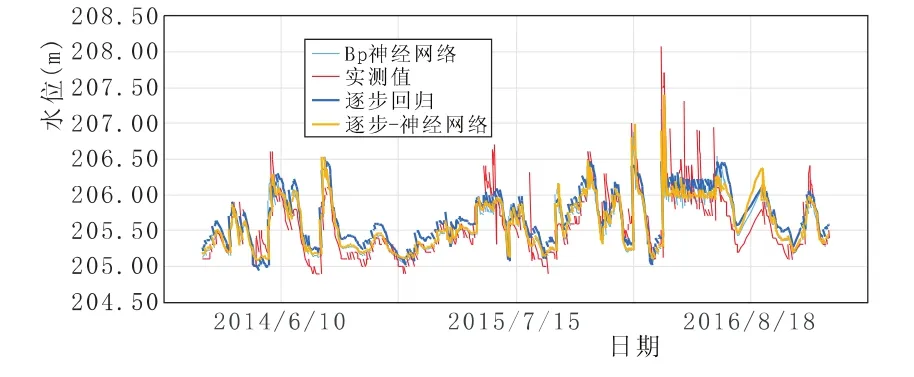
圖5 UP403測壓管實測水位與回歸值過程線

從整體上來講，三種模型的擬合曲線與原始記錄曲線走勢較為一致，擬合效果較好。UP401相關系數達到0.98以上，相關性強；UP402相關系數達到0.89以上，相關性較好；UP403相關系數達到0.77以上，相關性一般，表明距上游水位越遠，管水位的受影響因素越復雜，如壩基滲流、下游水位等，說明在缺乏相關資料的情況下，采用統計模型進行分析所達到的精度有限。

三種模型中，神經網絡的擬合精度較統計模型明顯提高，以UP402測壓管殘差總方差為例，殘差總方差為0.21，其次為0.22，最后為0.26，分別較統計模型分別提高31%、23%，表明隨著輸入層節點增多，擬合效果越好。而且，越往下游，采用神經網絡求得的效果越好。

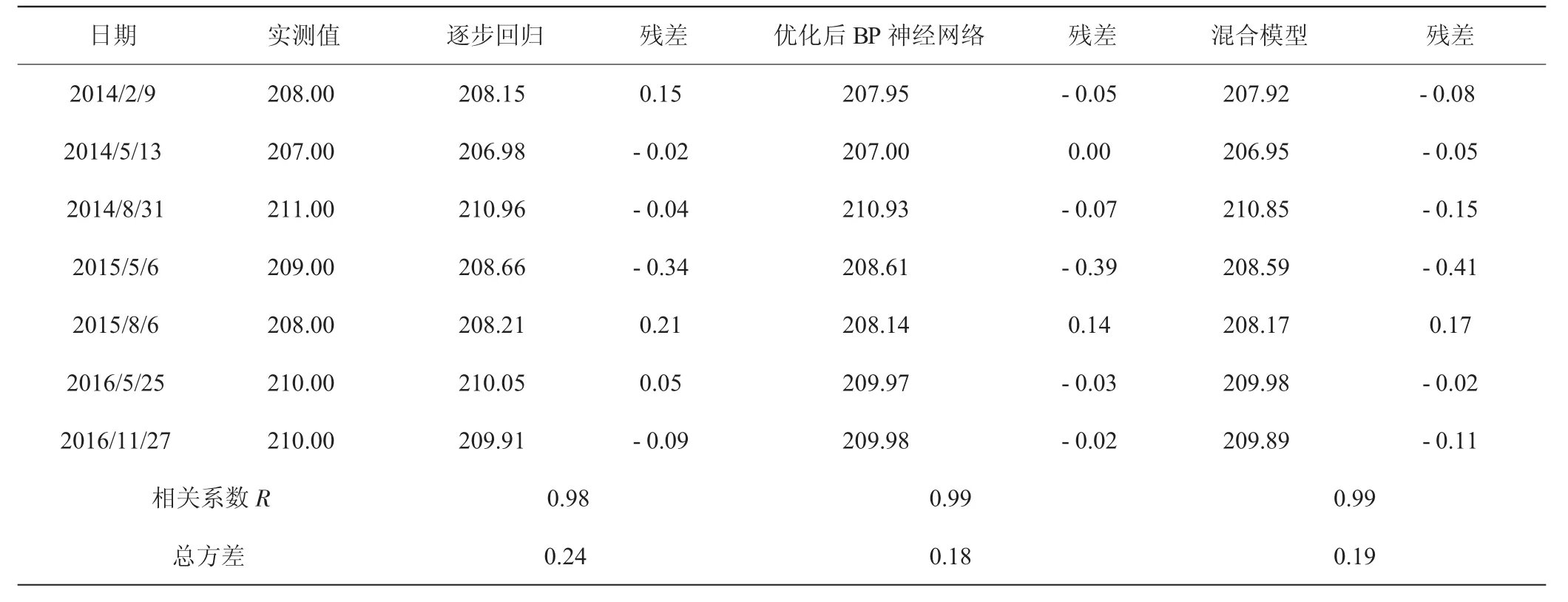
表1 UP401管水位三種模型結果對比

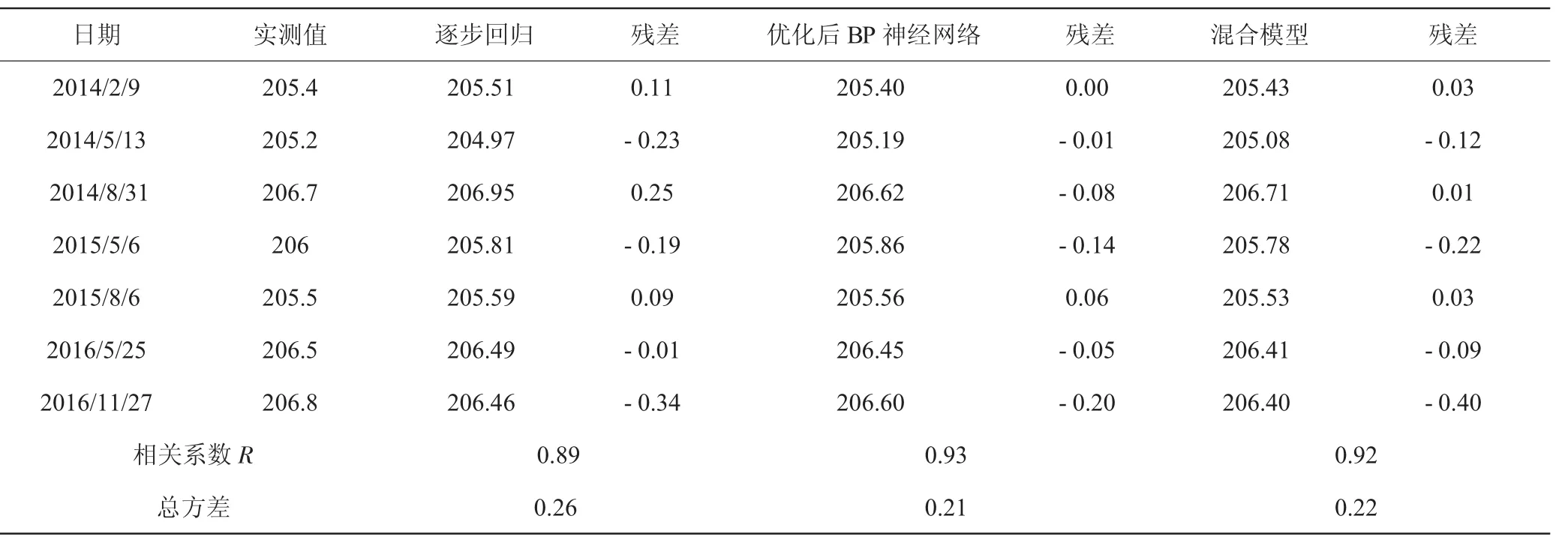
表2 UP402管水位三種模型結果對比

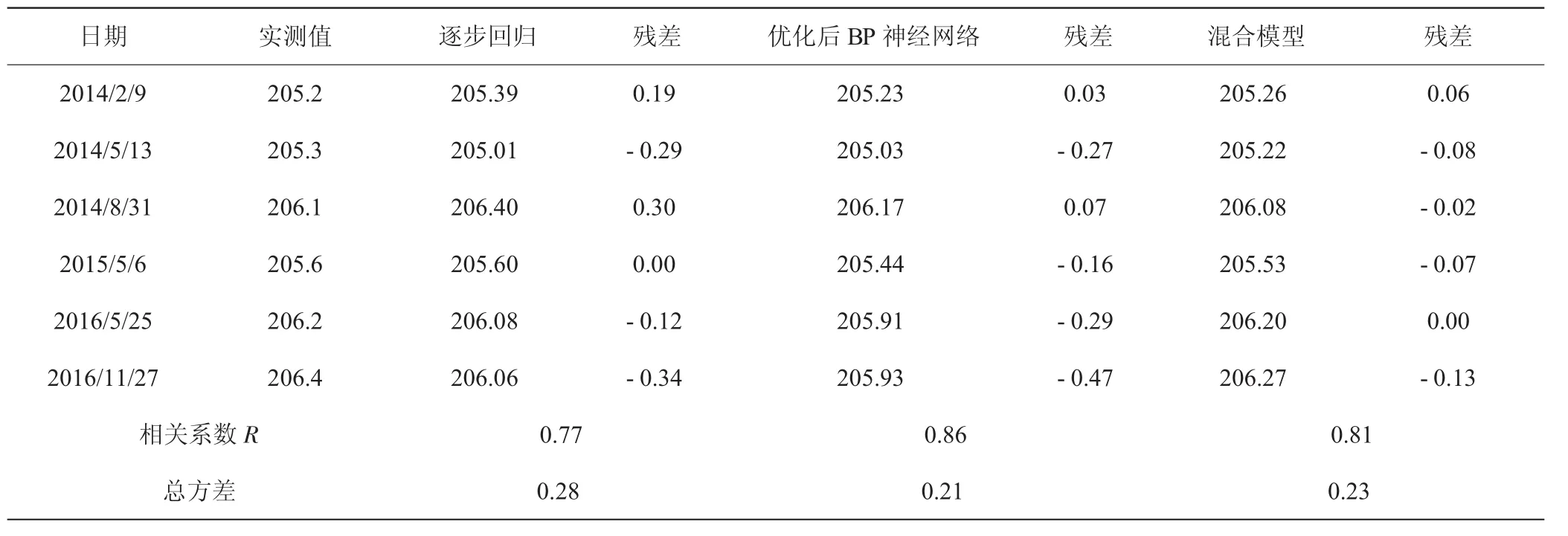
表3 UP403管水位三種模型結果對比

4 結論

(1)對于土石壩心墻上游，采用逐步回歸模型及神經網絡，擬合精度較高，能達到預測要求。

(2)當位于心墻下游時，逐步回歸模型擬合精度下降較快，而采用神經網絡模型，擬合效果明顯優于逐步回歸模型，預測效果最高提高了30%以上。

(3)對于靠近心墻上游測壓管，采用統計模型即可達到精度要求，而位于心墻下游，當統計模型精度達不到要求時，可采用神經網絡提高預測效果。