冬棗輔助采摘車車架結構優化設計——基于層次分析法

劉廣新，王淑君，趙玉剛，蔡善儒

(山東理工大學a.機械工程學院；b.農業工程與食品科學學院 ，山東 淄博 255049)

0 引言

沾化冬棗味道甘甜，皮薄肉脆，種植于山東、陜西等地。冬棗的產量逐年增加，到2020年產值可達40億元。但是，在其采摘過程缺少機械化，出現了采摘效率低、勞動量大、勞動力短缺等問題。為此，設計了一款適合冬棗種植情況的冬棗采摘車。該車的主要工作環境是野外棗園，地面松軟且凹凸不平，受力情況較普通車輛復雜。若車架質量過大,會影響整車的動力配置，提高整車研究成本；同時，會造成冗余材料的浪費，不能發揮材料的最大性能，影響整車續航時間。因此，性能良好的車架成為保證輔助人工采摘車工作性能的關鍵環節。

冬棗輔助人工采摘車車架的結構設計在現階段主要依靠經傳統經驗設計，而這類方法一般通過增加各組件的厚度來解決強度問題，但隨之而來的是車架質量過大，造成材料的浪費。近年來，專家學者紛紛借助CAD/CAE軟件來獲得最優機械性能。周方思[1]等根據有限元靜力學分析結果，結合拓撲優化的方法對除草機車架進行減重優化。毛鵬軍[2]等在研制的煙田輔助采收機的基礎上，使用ANSYS Workbench對車架進行有限元分析，根據分析結果做了輕量化設計。上述研究方法，通常根據材料的最大屈服強度，通過減少材料達到減輕質量的目標，但動態性能卻沒有得到提升。本文在有限元靜動力學分析的基礎上，結合靈敏度分析方法與層次分析法的各自特點對車架結構進行多目標優化設計，并進行優化前后結果比較。結果表明：使用靈敏度分析法與層次分析法相結合，對車架多目標優化是可靠與合理的。

1 車架有限元靜動力學分析

為了得到車架模型的最大變形量和低階固有頻率，需要對車架模型進行有限元靜動力學分析[3]。

1.1 車架有限元建模

根據車架實際尺寸大小，在Pro/E軟件中建立車架參數化模型。其中，車架全長1.950m，寬0.96m，高0.27m。車架各部件均由不同厚度的矩形鋼管焊接而成，材料為易于焊接的Q235，質量為132.65kg。車架簡化模型和部件編號如圖1 所示。

為了提高有限元分析的準確性和縮短計算時間，一般要對對車架模型中小的倒角、圓角、孔等特征進行相應的簡化[4]。將建立好的車架模型通過軟件間的友好鏈接通道導入AWB中，以免丟失數據和模型特征。在AWB中選擇SOLID187單元劃分四面體單元，尺寸設置為20mm，劃分網格后生成節點數129 607個，單元數66 168個，劃分網格后的模型如圖2所示。

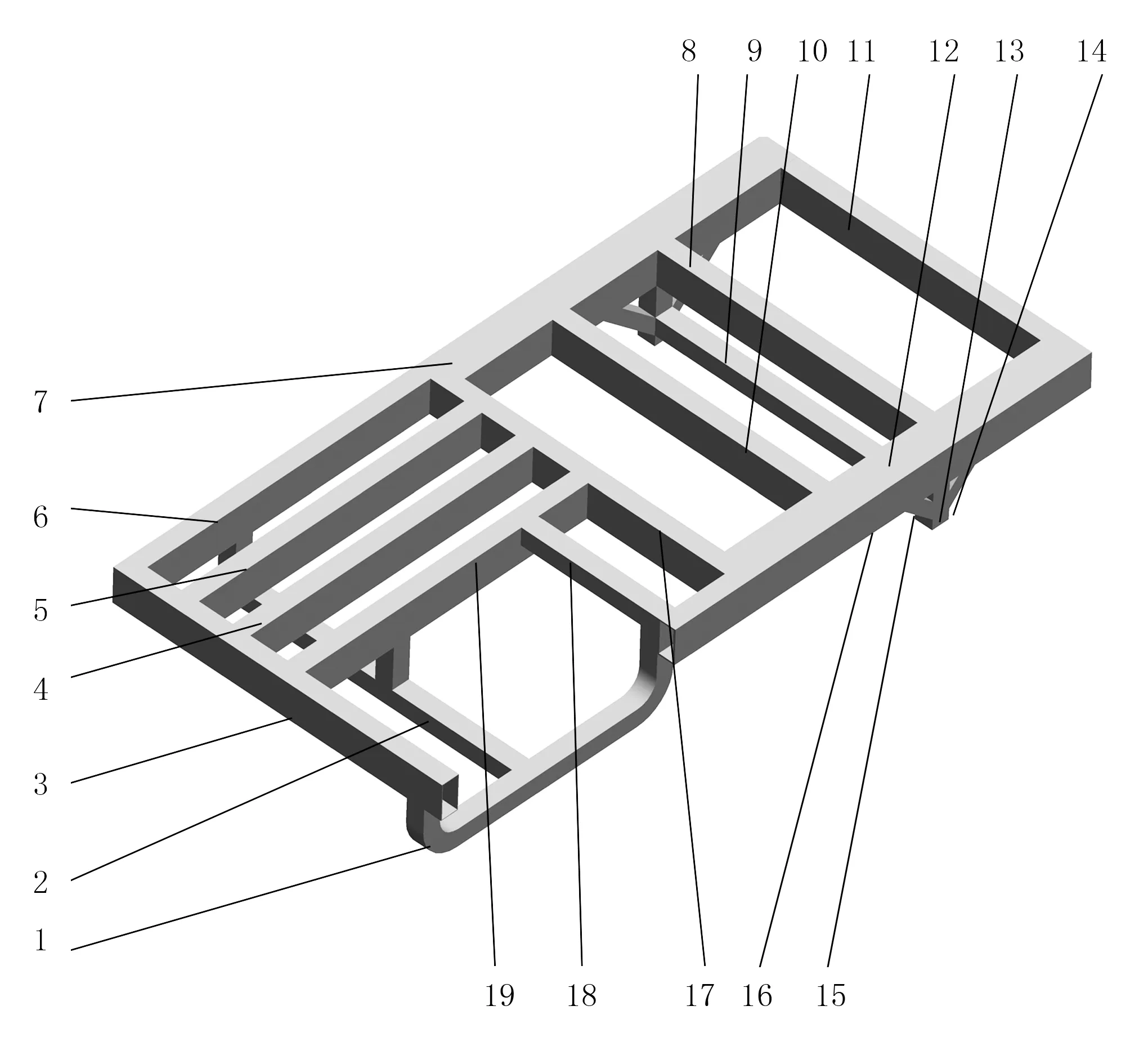
1.駕駛室U型梁 2.前輪軸固定梁 3.前防撞梁 4.前作業單元副支撐梁 5.前抗扭組件 6.左主縱梁 7.左副縱梁 8.后作業單元支撐主梁 9.后輪軸固定梁 10.后作業的單元支撐副梁 11.后防撞梁 12.右副縱梁 13. 后輪軸支撐柱 14.后輪軸支撐住后斜支撐 15.后輪軸支撐住前斜支撐 16.右主縱梁 17.中間防扭組 18.座椅支撐梁 19.前作業單元主支撐梁

圖2 車架有限元模型

1.2 車架模型合理性實驗驗證

合理、準確的車架模型能夠為車架結構優化提供準確的數據。為此，設計了車架模型合理性驗證實驗，測量了停放于水平地面的車架不同位置的應力，具體測量點分布位置如圖3所示。整車空載時布置測量點，滿載時加載的質量主要是駕駛員(68.2kg)、前作業單元作業者(66.1kg)、后作業單元作業者(70.2kg),載荷穩定后測量[5]。實驗設備：德國IMC公司研制的IMCCL-5016應變測試系統、BX120-2AA應變片、電動角磨機、101膠水、砂紙、FAMOS軟件及體重秤等。

圖3 車架應力測量點散布圖

由表1中應力測量值與仿真值對比可知：除 1處和7處的測量數據與仿真數據相對誤差較大外，其它點的誤差均在15%以內，誤差均在許可范圍內，所建立參數化模型準確合理。

表1 應力測量值與仿真值

1.3 車架極限工況下靜力學分析

結合車架實際工作狀態對車架模型做有限元分析，能夠提供合理、有效的優化數據。為此，選取車架極限靜止狀態對車架模型進行有限元分析。車架極限狀態下，右前輪和左后輪軸固定處的約束為位移約束。冬棗輔助采摘車車架用于承載采摘作業單元與采摘作業人員(4 000N)、蓄電池組(3 400N)、液壓站(300N)、電動機、駕駛室和駕駛員(1 000N)等。其中，采摘作業人員和駕駛員體重均按70kg計算，電動機固定在后輪軸上質量不計。車架選用不同規格的矩形管焊接而成，材料均選用易于焊接的Q235。各部分均等效為集中載荷施加到對應位置，車架的自重通過材料屬性設置自動添加[5]。經AWB求解后的應力分布圖和總變形分布圖如圖4、圖5所示。

圖5 總變形分布圖

由圖4可以看出：車架的最大應力出現在左后輪軸固定處，為117.43MPa，遠小于車架的最大屈服極限強度235MPa，滿足車架強度設計要求，還有較大的設計余量。由圖5可以看出：車架的最大變形出現在右主縱梁與后防撞梁鏈接處，為1.804 5mm，遠小于車架最大變形量參考值。結合以上分析，在保證車架靜態極限工況下的性能下，可以對車架進行輕量化優化設計。

1.4 車架模態分析

模態分析是動力學分析的關鍵，車架的模態分析直接反映了車架結構動力學特性[6]。 在車架的模態分析中，各階模態所占有的權重隨模態頻率的增加而降低。在AWB中車架進行模態分析時，邊界條件為自由邊界，設置頻率最小為1Hz，最大為250Hz。由自由模態分析得到前4階模態如圖6～圖9 所示，對前4階振型進行描述如表2所示。

圖6 車架第7階模態云圖

圖7 車架第8階模態云圖

圖8 車架第9階模態云圖

圖9 車架第10階模態云圖

階數固有頻率/Hz振型情況784.61繞Z軸扭動894.33ZOY面內呈凹型9128.72XOZ面擺動10140.25XOZ面扭動

冬棗輔助采摘車車架的激勵主要由路面和電動機產生，其中路面激勵頻率不大于3Hz。冬棗輔助采摘車屬于微型電動車，車速最大40km/h時，發動機振動頻率可達80Hz，非常接近車架低階固有頻率，共振情況容易發生，影響車架性能[7]。因此，車架低階固有頻率需要提高。通過對車架前4階振型結果分析可知：車架各部件動剛度存在不足，需要對其進行優化設計。

2 車架參數靈敏度分析

靈敏度分析法可借助特定的數學方法計算出結構的性能參數隨設計變量變化的靈敏度，然后結合結構整體性能要求，合理、有效地選擇需要優化設計的部分[8]。該方法可以有效地找出對車架性能影響大小的設計變量,提高車架優化效率[9]。考慮到對車架整體性能的影響，選取了車架19個主要部件(見圖1)的厚度作為設計變量，將質量、低階頻率、總變形量作為影響車架性能的指標。利用AWB求解出19個設計變量對車架動靜態性能影響的靈敏度數據經過處理得到如圖10～圖12所示的質量、低階頻率、最大應力靈敏度分析圖。

圖10 質量靈敏度分析圖

圖11 低階頻率靈敏度分析圖

圖12 最大應力數靈敏度分析圖

其中，條形圖的長度表示參數對指標的影響程度，長度越長影響越大。零刻線以上的呈正相關，表示指標隨著設計變量的增加而增加，或指標隨著設計變量的減少而減少；反之，零刻線以下的呈負相關，表示指標隨著設計變量的增加而減少或指標隨著設計變量的減少而增加。

通過分析圖10～圖12可知：在19個設計變量中，編號2、4、5、14、15、18的部件厚度對3個指標的影響都很小，可以作為非關鍵設計變量，保留設計厚度不變，其余設計變量均作為關鍵設計變量。

3 車架數學模型建立與求解

車架輕量化設計不僅可以增加整車的續航時間，而且可以提高車架材料的使用率，減少材料與能源的浪費。車架的固有頻率提高可以有效地避開共振頻率，提高車架的動剛度。結合有限元靜動力學分析結果和靈敏度分析結果，將車架的質量和低階固有頻率作為優化目標。由于質量減少的同時車架的最大應力和最大變形也會隨之增加，這樣就會使車架輕量化設計失去意義，故限制極限工況下安全系數為1.5。結合靈敏度分析結果，以車架各組件的厚度作為設計變量，其中駕駛室U型梁x1，前防撞梁x3和后輪軸支撐柱x13下限2mm、上限4mm；左主縱梁x6，左副縱梁x7，后作業單元支撐主梁x8，后輪軸固定梁x9，后作業的單元支撐副梁x10，右副縱梁x12，右主縱梁x16，中間防扭組件x17和前作業單元主支撐梁x19的下限均為2mm、上限均為8mm；后防撞梁x11的下限為1mm、上限為3mm；其余部件厚度保持不變。在冬棗輔助采摘車車架模型中，車架質量、車架低階固有頻率、車架最大應力作為目標函數，定義19個變量，根據靈敏度分析結果選取13個變量作為設計參數組合(X)=g(x1,x3,x6,…,x13,x16,x17,x19)。車架結構優化設計數學模型為

將車架各組件厚度尺寸作為變量，代入上述數學模型反復迭代后求解得到5組車架設計方案非劣解，如表3所示，各方案對應的變量參數如表4所示。

表3 5組車架設計方案

續表3

表4 車架設計方案變量參數

4 層次分析法優化車架性能

車架的優化設計方案需要借助一定的評價方法來獲取最優設計。層次分析法是一種有效結合定性分析與定量分析的決策方法，能夠對一些較為復雜、模糊的問題做出簡便、靈活的決策[10]。其基本思想是：通過將復雜問題分解，按照支配關系形成遞階層結構，同時根據一定的比率標度，通過兩兩比較將判斷定量化，最終得到最優方案[11]。

4.1 層次結構模型建立

層次分析法模型分為3層，依次為目標層、準則層、方案層。其中，目標層為冬棗輔助采摘車車架的最優設計方案；準則層為車架的最大應力、車架的質量及車架的固有頻率。目標層由1個元素組成，準則層與方案層由多個元素組成，同一層的每個元素對上一層的影響不同。車架設計方案層次結構模型如圖13所示。

圖13 車架設計方案層次結構模型

4.2 優先級矩陣建立

在保證車架的強度和剛度前提下，車架的質量應當越小越好，也就是說車架質量的倒數越大越好。根據以上分析得到5種設計方案的質量倒數矩陣，即

Nm=(0.00803 0.00779 0.00777 0.00811

0.00798)

將得到車架的質量倒數矩陣中各元素進行比較，具體參見文獻[12]，得到矩陣為

Wm=

將矩陣Wm各列元素相加得到矩陣為

Qm=(0.94146 5.09371 5.10682 4.89271

4.97243)

將矩陣Wm各列元素分別除以矩陣Qm中對應列的元素所得的商相加再求平均值，得到的矩陣則為5種方案中車架質量優先級矩陣，即

Pm=(0.20237 0.19632 0.19582 0.20439

0.20111)

同理，則可以得到車架低階頻率和車架最大應力對應的優先級矩陣為

Pf=(0.20152 0.20257 0.20099 0.19774 0.19717)Pσ=0.19111 0.20537 0.20956 0.19258 0.20138)

4.3 判斷矩陣構建立

在層次分析法中，判斷矩陣常常采用Thomas L. Saaty提出的“1-9”標度法來建立。“1-9”標度法主要用于對相對重要性的數值表示，從而構建判斷矩陣[13]，如表5所示。在車架機構優化過程中，車架質量的降低可以有效地降低整車能耗，故車架質量比車架低階頻率和車架最大應力稍微重要。車架的低階頻率也會直接影響整車的動態性能，相比較而言車架最大應力稍微重要。根據以上分析，可以確定判斷矩陣I，即

由矩陣I求得λmax= 3.0536，一致性檢驗得CI=0.0268<0.1，通過一致性檢驗。

根據公式(2)，有

AT=λmaxAT

(2)

其中，A為判斷矩陣，λmax為矩陣A的最大特征值。計算出權重矩陣A，即

表5 因素重要度對比

4.4 最優解的確定

5種方案對應的各評判標準的優先級矩陣組成,矩陣P、矩陣A左乘矩陣P得到5個方案對應的量化指標為

AP=(0.20052 0.20029 0.19926 0.20080

0.20002)

根據上述計算結果，可以得出冬棗輔助采摘車車架結構優化設計方案優劣順序為：方案4、方案1、方案2、方案5、方案3。以上5種方案均優于原方案，且方案4為最優設計方案。車架優化后各參數對比如表6所示。

表6 車架優化前后各參數對比

其中，較優化前車架總質量降低 7.01%，低階頻率提高2.17%，最大應力降低7.32%，動靜態性能都有所提高。車架優化后，冬棗輔助采摘車樣機的裝配過程中效果良好，整車性能得到提升。圖14為冬棗輔助采摘車樣車。

圖14 冬棗輔助采摘車

5 結論

將多目標優化應用到冬棗輔助采摘車車架的性能優化中，建立了以車架質量、最大應力和低階固有頻率為優化目標函數的數學模型，優化了車架多個性能參數。采用層次分析法優化后，較優化前車架總質量降低 7.01%，低階頻率提高2.17%，最大應力降低7.32%，應力較優化前均勻分布，整車動靜性能均有提高。