基于船舶效益和能效管理的航速決策研究

馬來好, 茆沐嘉, 黨 坤

(1.大連海事大學 輪機工程學院，遼寧 大連 116026；2.南通航運職業技術學院 輪機工程系，江蘇 南通 226000)

0 引 言

船舶營運效益決定了航運公司的生存以及發展。而在船舶營運過程中，航速的高低直接關系船舶的變動成本大小(燃油費用等)，雖然降低航速可以達到壓縮燃油成本的目的，但是另一方面，降速航行會延長航次時間，增加固定成本，還有可能錯過其它貨載機會，另外隨著主機轉速的降低，主機的工況點也會偏離設計工況，其油耗量反而上升，不利于船舶的節能減排。可見，航速優化是實現營運效益的一項主要和關鍵工作。其需要通過系統科學的分析和比較，綜合選擇船舶航速，以實現船舶營運效益的最大化。文獻[1]中運用 VS2005 和SQL Server 2005聯合開發了船舶航次效益估算系統，大大提高了航次效益估算的效率；文獻[2]中建立了內河船舶EEOI與主機轉速關系模型，優化結果表明,在預定時間內油耗節省0.8t，EEOI減少1.64%；文獻[3]中構建了以航次日均盈利額最大化為目標的最佳航速優化模型，并指出日均盈利額主要受航速及燃油價格波動的影響；德國勞氏船級社指出采用低于當前航速可謂集裝箱船隊帶來經濟利益[4]；Ronen(1982)建立了以燃油成本最小和利潤最大的航速優化數學模型，并采用數學求導的方法對不定期船舶的最佳航速進行求解[5]；Fagerholt(2010)建立了以航次燃油消耗總量最小為目標的航速優化數學模型，并采用抵達時間離散化的啟發式算法對模型進行求解[6]。本文將燃油價格和運價進行組合，考慮不同情形應用遺傳算法對船舶航次營運效益和EEOI最優下的航速進行研究。

1 船舶營運效益估算模型

1.1 船舶航次時間

本文所研究的船舶營運航次是指從裝貨港裝貨開始，裝貨航行至卸貨港卸完所載貨物為止，即航次時間為：

(1)

式中：T為航次總時間，單位為d；l為航次航程，單位為nm；v為航次航速，單位為kn；Tl為在裝貨港裝貨停泊時間，單位為d；Td為卸貨港卸貨停泊時間，單位為d；Tm為航次錨泊時間，單位為d。

1.2 船舶航次收入

對于船舶航次收入，是指航運企業為貨主完成航次貨物運輸任務后所應該收取的費用，這里忽略滯期費、虧艙費等，則：

(2)

式中，D為船舶航次總收入，單位為美元；ri為貨物i的運費率(運價)，單位為美元/t；Qi為貨物i的載貨噸數，單位為t。

1.3 船舶航次成本

對于船舶航次成本，包括航次變動成本和固定成本。其中，航次變動成本包括燃油費用、港口費用，而港口費用涉及裝貨港、卸貨港。航次固定成本包括船員工資、潤料費、備件費、修理費、管理費用以及其他固定費用。由于鍋爐、發電機油耗基本不變，可作為固定成本。因此,船舶航次成本可以表示為：

ClpTl+CdpTd

(3)

式中，p為燃油價格，美元/t；Clp為裝貨港港口使費，美元/d；Cdp為卸貨港港口使費，美元/d；C0為船舶營運每日固定成本，美元/d；qme為主機每日油耗量，t/d，其與船舶航速具有如下關系：

qme=q0(v/v0)3

(4)

式中，q0為船舶航速為v0時對應的主機油耗量，t/d。

1.4 船舶航次營運效益估算模型

對于船舶航次營運效益估算，航運公司常見的兩種優化目標分別為日收益最大和航次收益最大。以船舶航次收益為優化目標，聯立上式(1)～(4)，可以得到如下模型：

pqb(Tl+Td+Tm)-ClpTl-CdpTd

(5)

約束條件為：

(1)限制航速的可行范圍。

vmin≤v≤vmax

(6)

(2)航次租船合同時間窗限制。根據船舶航次租船合同，貨主和船東會約定一個受載期和解約日，即到達卸貨港最早和最晚時間為：

(7)

2 船舶能效指數估算模型

根據EEOI自愿使用指南，EEOI是指船舶單位航次的CO2排放量：

(8)

式中，j為燃油類型；FCj為燃油j的消耗量；CFj為CO2排放因子，取3.114；mcargo為貨物總噸；D為船舶航行里程。

根據式(8)，結合式(1)～(3)，可以得到：

(9)

式(9)的約束條件同船舶航次營運效益估算模型。根據上述推導的式(6)、(7)，可知所建立的船舶航次營運效益、能效指數估算模型是以船舶航速為自變量并具有約束的非線性方程，其最優問題本文采用遺傳算法進行求解。

3 計算結果與分析

某航運公司船舶從事航次租船，其主要船舶營運參數如表1所示。

表1 船舶營運參數

由于船舶營運效益受到航速、燃油價格以及市場運價的影響，為了較為全面分析航速對船舶營運效益以及船舶能效指數的影響，這里將燃油價格和市場運價進行組合，分成4種情形，①低油價、低運價；②低油價、高運價；③高油價、低運價；④高油價、高運價。其中，根據文獻[7]中提供的燃油價格數據將高燃油價格為680 $/t，低燃油價格為102 $/t，根據該營運船舶載貨的歷史資料，將低運價定為10 $/t，高運價定為100 $/t。在上述4中情形下，基于上述模型分別研究在上述組合下船舶營運效益和EEOI變化，以及對應的最優值，計算結果如圖1～4所示。

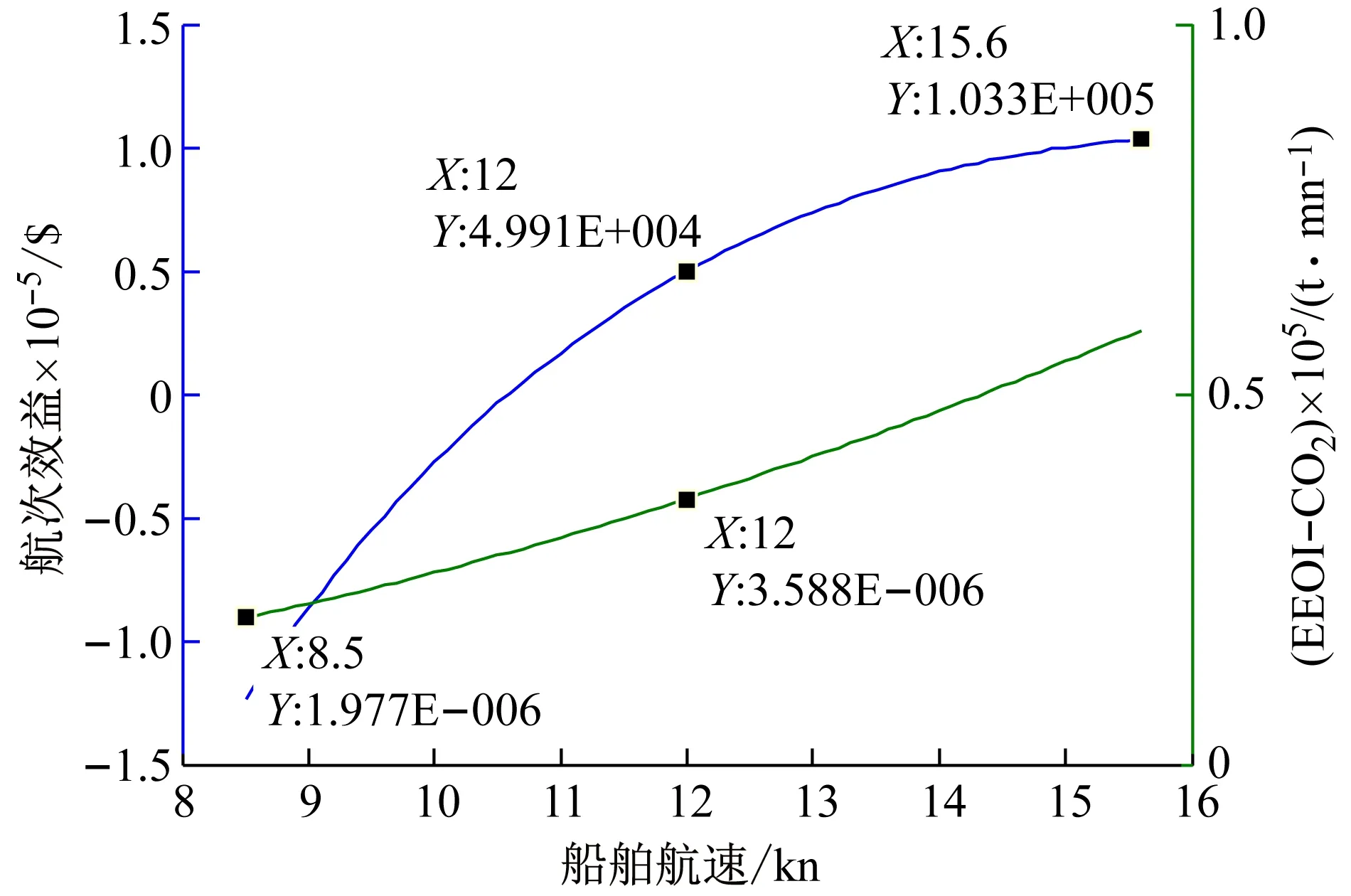
圖1 低油價、低運價下的船舶航次效益和EEOI

圖1為低油價、低運價下的船舶航次效益和EEOI隨航速變化情況。可以看出，在低油價和低運價下，該船舶的舶航次效益隨著航速的增加而增加，船舶EEOI也是隨著航速的增加而增大，優化出的航速分別對應船舶航速的兩個最值，即在航速為15.6 kn取得航次效益最大，而在航速為8.5 kn時取得EEOI最低。在航次效益最優航速下取得航次效益要遠大于營運航速下取得的航次效益，在最優EEOI航速下雖然可以減少CO2排放量，但是航次效益將出現虧損。

圖2為低油價、高運價下的船舶航次效益和EEOI隨航速變化情況。可以看出，在低油價和高運價下，該船舶的舶航次效益和EEOI隨航速變化情況與低油價、低運價下基本相同。航速為15.6 kn取得航次效益最大，航速為8.5 kn時取得EEOI最低，分別優于該船舶在營運航速時的航次效益和EEOI，不同的是在最優EEOI航速下，該船舶航次效益仍然盈利。

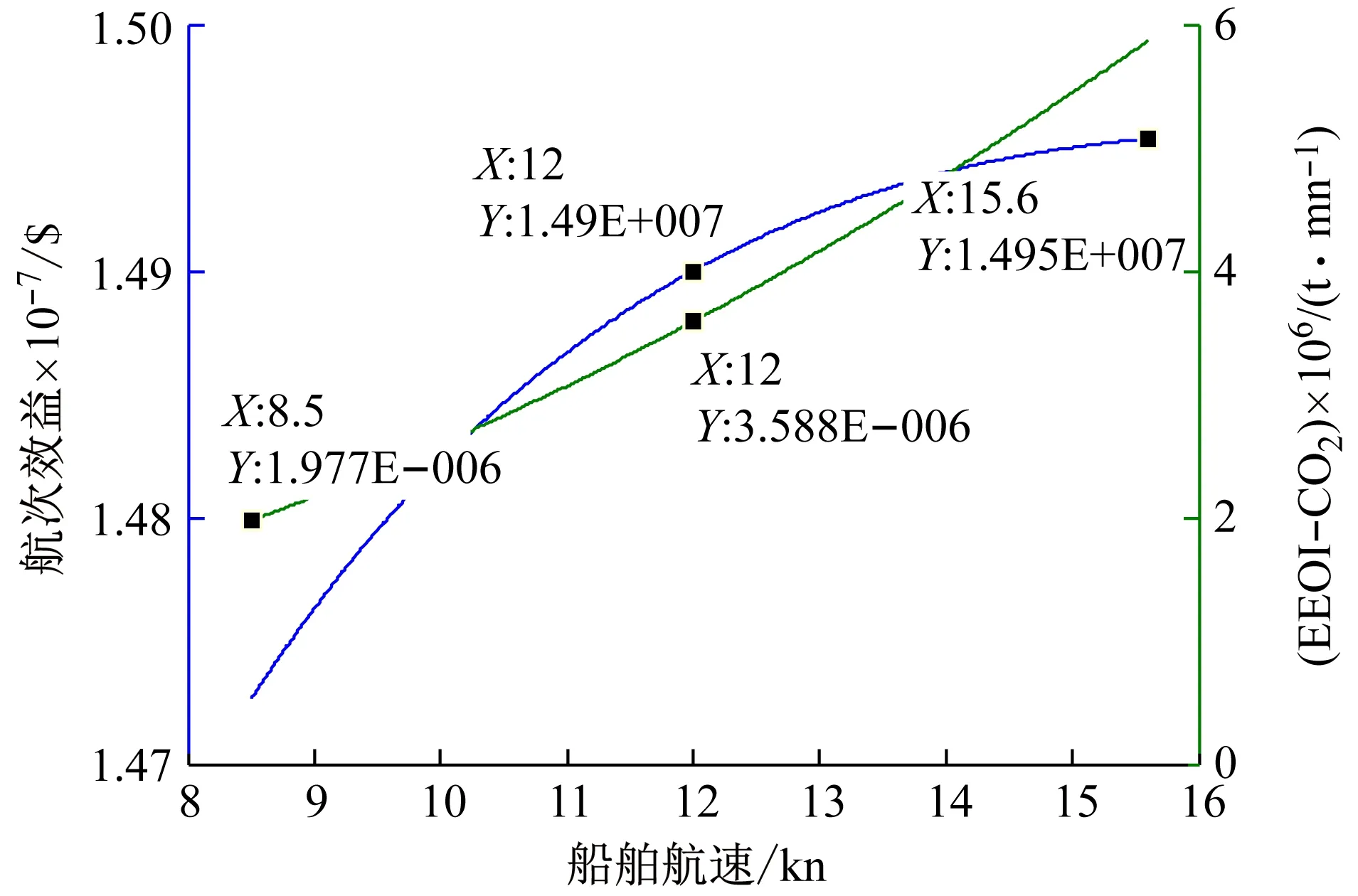
圖2 低油價、高運價下的船舶航次效益和EEOI

圖3為高油價、低運價下的船舶航次效益和EEOI隨航速變化情況。可以看出，在高油價、低運價下，船舶EEOI也是隨著航速的增加而增大，在航速為8.5 kn時EEOI最低。而該船舶的航次效益隨著航速的增加虧損越大，并不是在航速最小時虧損最小，而是在航速為8.87 kn時，該船舶虧損最小，能夠比營運航速下少虧損20%。

圖3 高油價、低運價的船舶航次效益和EEOI

圖4為高油價、高運價下的船舶航次效益和EEOI隨航速變化情況。可以看出，在高油價、高運價下，與上述情形相同，船舶EEOI也是隨著航速的增加而增大，在航速為8.5 kn時EEOI最低。而該船舶的航次效益隨著航速的增加盈利越小，在航速為8.87 kn時，該船舶航次效益最大，優于營運航速下的航次效益和EEOI。

4 結 語

本文對油價和運價分成4種組合方式進行研究航次租船下的航次效益和船舶能效指數EEOI，通過模型計算，航次效益優化航速和EEOI優化航速均優于正常營運航速時的船舶航次效益和EEOI。其中在低油價和低運價、低油價和高運價下，建議船舶以較高航速進行運營，在高油價和低運價、高油價和高運價下，建議船舶以略高于最低航速進行運營。特別是在目前航運市場低迷情況下，所建立的航次效益和EEOI估算模型，能夠測算航次效益、EEOI以及最優航速，選擇指導航速，可為航運相關部門提供一定的參考。

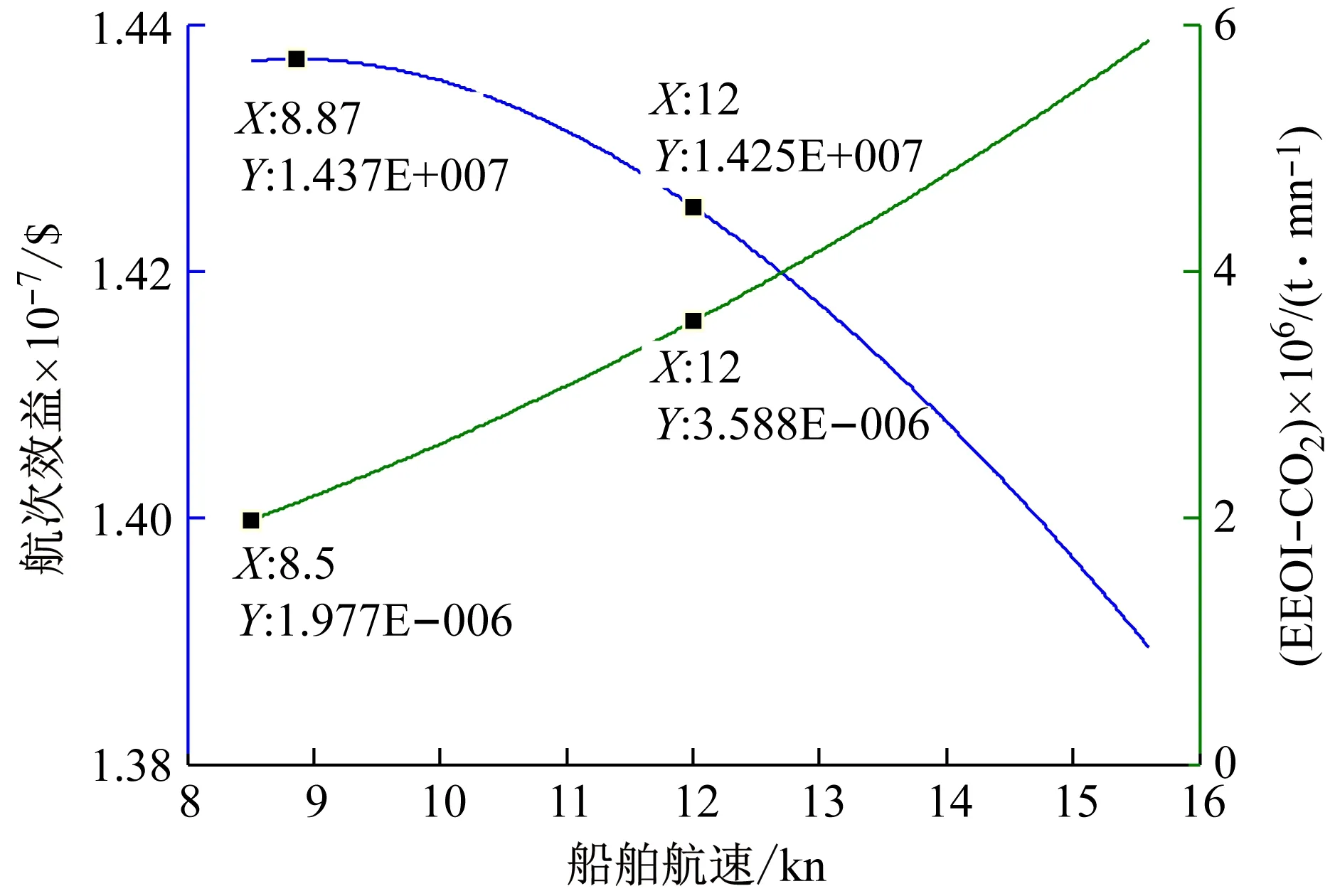
圖4 高油價、高運價下的船舶航次效益和EEOI