井筒貯礦對放礦磨損影響分析

詹森昌

（江西銅業集團公司德興銅礦，江西 德興 334224）

1 引言

在溜井放礦過程中，礦石在井筒中移動，礦石與四周井壁接觸，井壁產生磨損。尤其是貯礦段上部的井空部分，卸礦的礦石對井壁的局部撞擊而產生局部磨損。雖是局部磨損，但隨著撞擊次數的增加，磨損部位會逐漸擴大，對生產和安全造成很大影響，嚴重時導致井筒報廢。

在井筒貯滿礦時進行放礦，井壁受到礦石的磨損是緩慢的，全井筒的磨損是均勻的、有規律的，是可預測的。現結合德興銅礦滿井放礦實例，通過實測數據的分析，研究井筒磨損規律。

2 井筒中貯礦對井壁產生的壓力

井筒中的礦石，其對井壁產生的壓力分布，不同于液體的直角三角形分布，也不同于一個完整的固體對井壁不產生壓力。井筒中散體礦石對井壁產生的壓力是均勻分布的，井筒四周和上下都是相等的，只是與礦石性質和井筒半徑有關。其壓力計算式［1］：

式中：P為井筒中貯礦對井壁產生的壓強，N/m2；r為井筒半徑，m；γ為礦石的松散體重。t/m3；α為礦石與井壁的摩擦角，度。

根據計算式（1），可作出貯礦對井壁產生的壓力分布示意圖如圖1。

3 井筒貯礦段井壁磨損規律

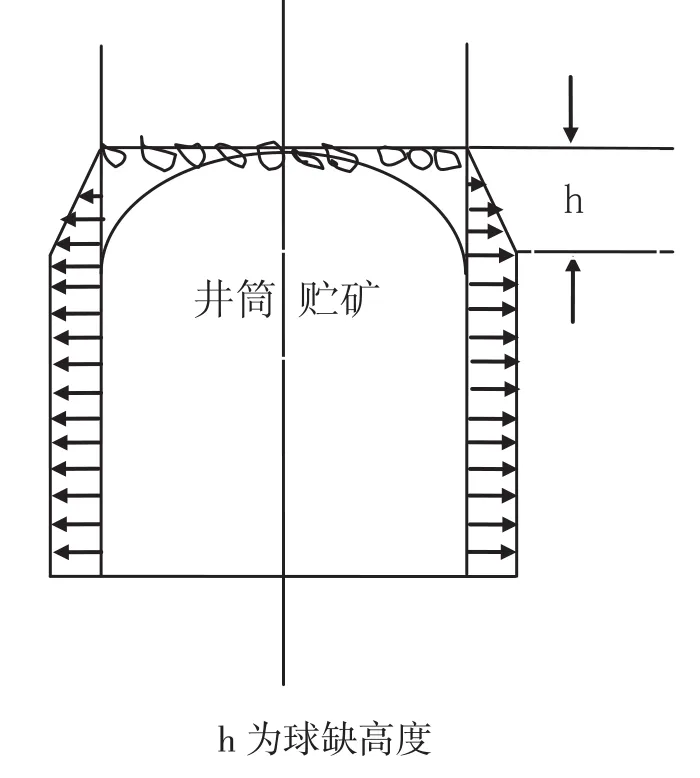
圖1 貯礦對井壁的壓力分布示意圖

溜井放礦過程中，貯礦段的礦石移動是緩慢、均勻下降，四周的礦石與井壁接觸，產生磨損。其磨損表現為：磨損速度較小且均勻，井壁光滑［2］。礦石對井壁磨損輕微，溜井周邊磨損均勻［3］。貯礦段溜井磨損均勻，上下非常接近［4］。全溜井井壁光滑、完整、磨損輕微［5］。

根據貯礦對井壁產生的側壓力是均勻分布，和上述文獻中表述的井壁產生的磨損現象，可以得出井壁磨損規律是：在溜井放礦過程中，貯礦段井壁產生的磨損，是以井筒中心線為中心，井壁的四周磨損擴大是均勻的、相等的，上下是相近的。

4 溜井井筒磨損計算式

根據上述溜井放礦井壁產生的磨損規律，在不同直徑的井筒用相應的1m高的礦石，從井筒上部向下摩擦（放礦）一次，井壁四周磨損擴大的量是非常的微小，但是相同的；每次產生的磨損量都是一樣的。因此，只要知道1m高的礦石與井壁摩擦（放礦）次數，就能計算出相應放出的礦石高度Δh，計算出井壁磨損擴大量和相應放出的礦石量，其計算式［6］：

式中：q為井筒直徑磨損擴大0.1m時放出的礦石量，萬t；S為井筒斷面積，m2;H為相應井筒直徑的高度為1m的礦石，m；γ為礦石松散體重，t/m3；N1為井筒直徑磨損擴大0.1m時，1m高度礦石與井壁的摩擦次數，萬次；Δh為q礦石量構成的礦石高度，等于HN1乘積，m。

式（2）是沒有考慮井筒貯礦對井壁產生側壓力條件下，井筒直徑磨損擴大0.1m時放出的礦石量。但是兩個物體在摩擦過程中，外部壓力加大時，磨損速度是會加快的。溜井井壁受到貯礦產生的側壓力，如式（1）所示，是與井筒半徑成性線正比的。因此，溜井放礦時，礦石與井壁產生的摩擦損失，也會隨著井筒半徑的磨損擴大，側壓力增加，磨損速度也會隨之增大。

假設，溜井放礦時，井壁磨損擴大的量，與井壁受到貯礦產生的側壓力成線性正比。即在各種井筒半徑時，井壁受到高度為1m的礦石摩擦次數為Ni，井壁產生的磨損擴大量為Δr，與考慮貯礦側壓力影響的初次摩擦次數為N相比，他們存在Ni=Nr1/ri；Δ hi=Δh r1/ ri關系，井筒磨損擴大量與放礦量之間存在如下關系：

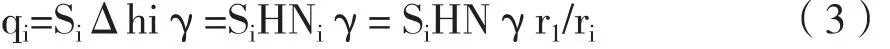
式中：qi為井筒半徑為ri時井壁磨損擴大Δr放出礦石量，萬t；Si為井筒半徑ri時的斷面積，m2；r1為井筒初始半徑，m；ri為當時的井筒半徑，m；Ni為井筒半徑為ri時，井壁磨損擴大Δr需1m高的礦石與井壁的摩擦次數，萬次；N為考慮貯礦對井壁產生側壓力時的初次摩擦次數，萬次；Δhi為qi礦石量構成的礦石高度，等于HNi乘積，m；其它同上。

現以德興銅礦1號溜井的數據進行分析。

原始數據：初始井筒半徑r1=3m，累計放礦量Q=1014.4萬t，井筒磨損擴大至r=3.655m。

4.1 求初次摩擦次數N

式（3）中Si、ri都是變量，必須把兩者相乘使其成為一個變量，進而求出N，把井筒半徑從r1=3m磨損擴大至r=3.655m，按Δr=0.05 m分成14檔，并把各檔的井筒斷面積Si乘以r1/ri得出Sir1/ri面積，如表1。

把式（3）中qi相加，得出累計的放礦量Q：

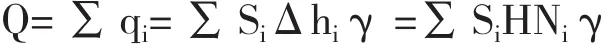
根據式（4）得：

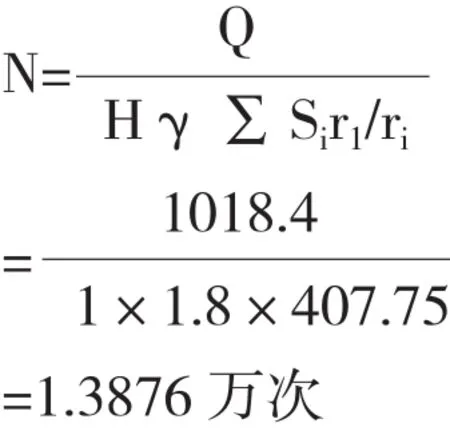
式中：符號意義同上。

4.2 多項式的計算式

根據（4）式得：

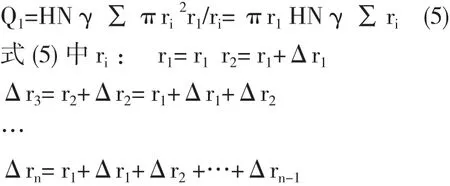
令 Δr1=Δr2=…=Δrn-1

得 ∑ ri=n r1+0.025n(n-1)

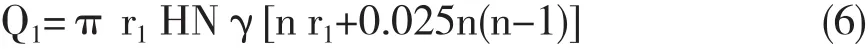
式中：n為多少個Δr項數，其它同上。

式(6) 計算出的各檔放礦量Q1，見表1。

4.3 積分式計算式

根據表1和式（4）計算得的初次摩檫次數N=1.3876萬次，它是井筒磨損擴大Δr=0.05m時，所需1m高礦石摩檫井壁的次數。也就是說，在不同的Δr值，就有相應的N值，若把各個不同Δr值換算成相同的一個Δr值時，其各個N、Δh值是相同的。如上面提到的(6)式中的Δr由0.05m變換成1m后，其計算出的K(=Δh/Δr)值和（9）式中的大小就一樣了。即：

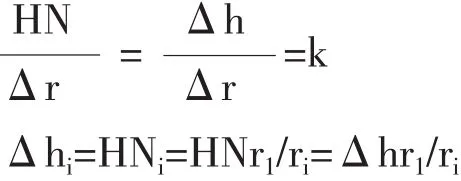
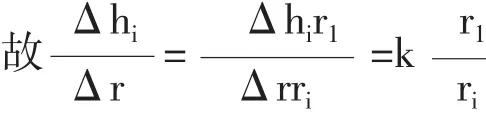
把式(7)中的Δhi代入(3)式得：

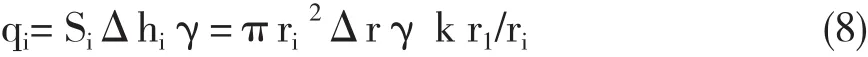
當Δr 0，qi0，對(8)式積分

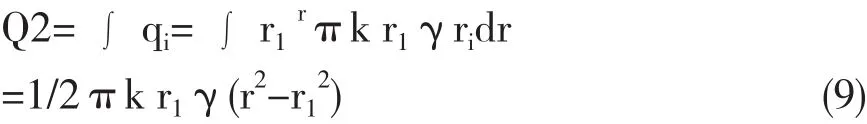
式中：符號意義同上。

把 Q=1018.4萬 t，r1=3m，r=3.655m 代入式 (9)，得：K=27.543

式（9）計算出的各檔放礦量Q2，見表1。

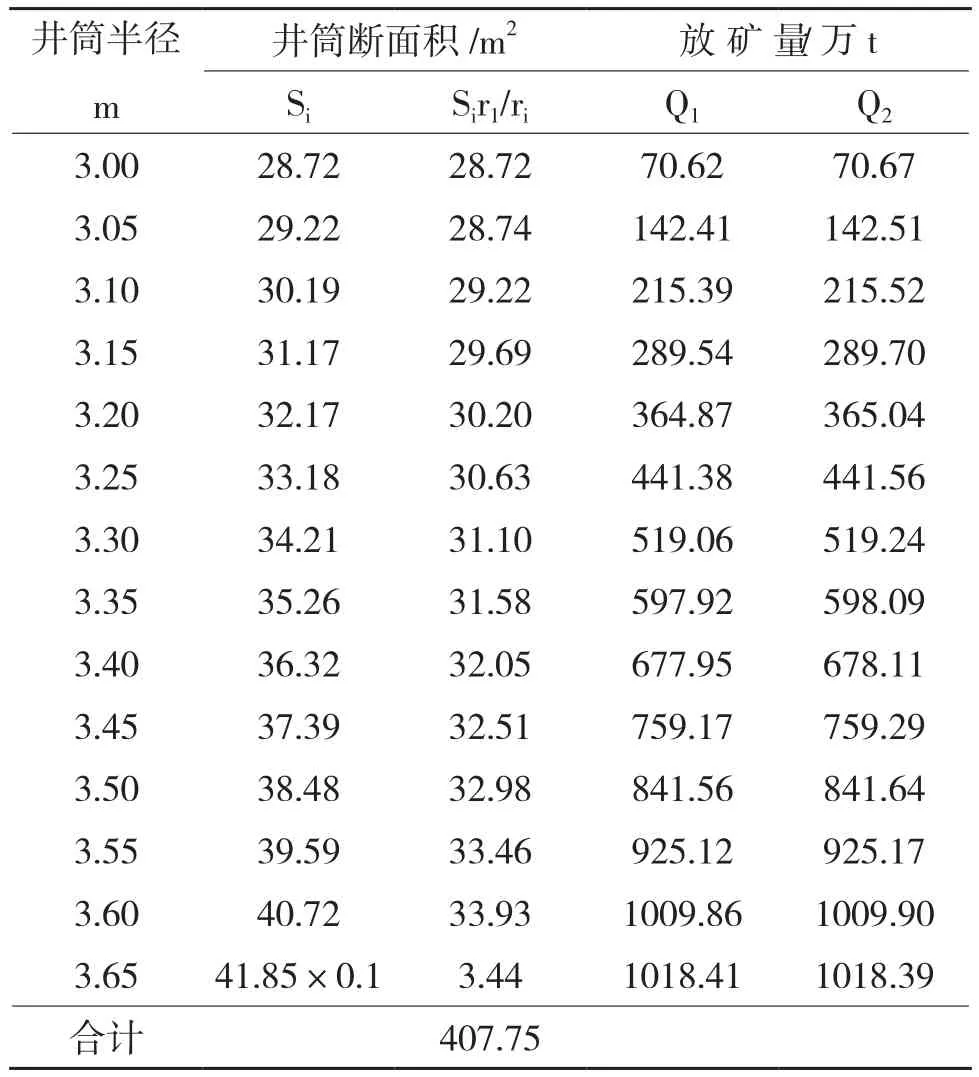
表1 井筒斷面積、摩擦次數、放礦量計算表

從表1中的Q1、Q2數據可看出，（6）式和（9）式計算出的放礦量，誤差在0.07%以內，說明推導是正確的。

另外，計算式（9）中的k，表面上是個無名數，實質上是井筒半徑磨損擴大時，需用H=1m高的礦石摩擦井壁的次數。式（6）和表1中N=1.3876萬次，是井筒半徑磨損擴大0.05m時所需的摩擦次數，若變換Δr=1m時，K=HN=27.752萬次，與式（9）中的k=27.543基本吻合，誤差為0.75%。

5 考慮與未考慮貯礦側壓力對井壁磨損產生影響的比較

5.1 放礦量比較

未考慮貯礦側壓力影響的計算式［7］：

式中：k′=24.7525；其它同上。

考慮貯礦側壓力影響的計算式：

式中：符號的意義同上。

兩者放礦量和磨損速度的計算結果，見表2。

表2 放礦量與磨損速度計算表

5.2 圖形比較

“采礦技術”2016年4期“溜井放礦量與磨損量計算式的數模”［7］提及，它們之間關系可用圓臺體的數學模型來表示，如圖2。當溜井初始半徑r1確定后，隨著放出礦石高度Δh =NH的增加，放出礦石量ΔQ的增加，井筒半徑隨之擴大Δr，ΔQ（Δv）、Δh、Δr三者呈圓臺體參數關系。圓臺體斜面與水平面夾角α是不變的，故K=Δh/Δr是一個常數。

當考慮側壓力影響時，井壁磨損速度會隨著井筒半徑的磨損擴大，側壓力加大，磨損速度加快，摩擦次數減小，Δh 逐漸減小， 即

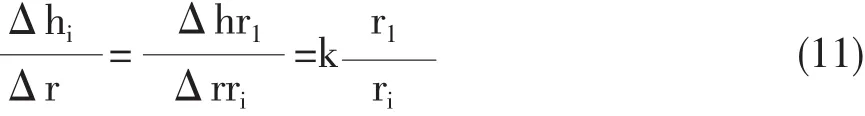
從式(11)中可看出，隨著ri的增加，逐漸變小，故圖2的圓臺體，變成曲面圓臺體，圖3。

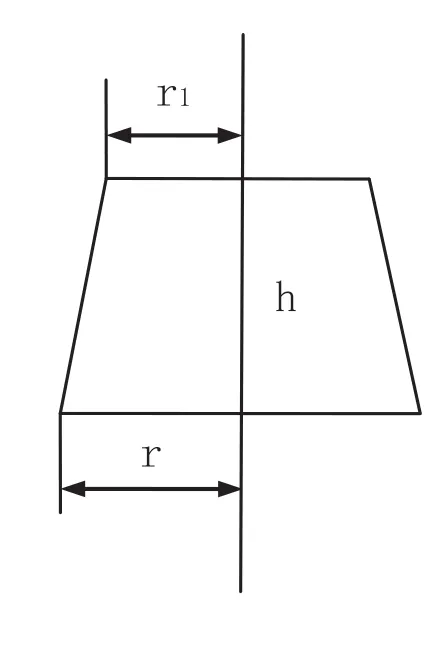
圖2 圓臺體

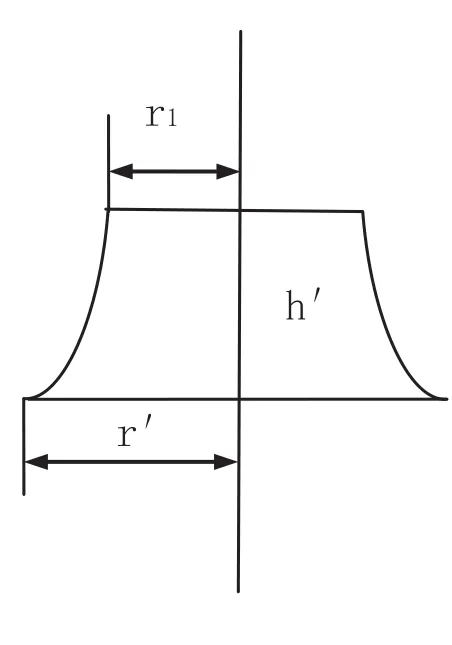
圖3 曲面圓 臺體

當兩個圓臺體的體積（放礦量）和初始半徑相等時，h＞h′，r＜r′。

總之，從表2、圖2、圖3數據看出，隨著放礦量的逐漸增加，井壁的磨損速度是下降的，未考慮貯礦側壓力影響時，下降速度更大。

5.3 磨損計算式檢驗

日本海田石灰石礦，該礦設計能力為30萬t/月，溜井井筒直徑5.0m，長度465m。為了控制好出礦品位和搞好溜井管理，與東京大學進行合作。在發表“關于礦石在大型溜井中流動的研究”（三之二）論文中提及：溜井井筒直徑實際成井時為5.5m，在放出261.5萬t礦石后，井筒直徑為7.15m;再放出338.8萬t后，井筒直徑為8.2m。在此基礎上，他們推導出放礦量與磨損量的關系式：

按上述公式計算，當放出216.5萬t礦石時，井筒磨損速度v0=0.003628m/萬t;再放出338.8萬t礦石時，按式（12）計算，井筒半徑r=4.596m，其誤差為：

（4.596-4.1）÷4.1=12.1%

按本文磨損計算式（9）計算，石灰石的松散體重γ=1.9t/m3，當放礦量216.5萬t時，K=6.106；在放出338.8萬t礦石時，r=4.24;其誤差率為：3.41%。

從數字上可看出，式（9）計算的誤差小，更接近實際；同時，從他們公布的大量監測數據看，溜井管理屬滿井放礦方式。

6 結論

（1）從表2中磨損速度反映出，考慮井筒貯礦的側壓力和未考慮的影響相比，前者井壁磨損速度加快；而總體的磨損速度是下降的。

（2）用日本海田石灰石礦公布的生產數據對磨損計算式進行驗算，誤差是小的，計算式是可信的。

（3）磨損計算式計算出的數據，可作為礦山規劃、設計和生產時參考。