數(shù)學模型的應用與數(shù)學應用能力培養(yǎng)的策略探究

☉江南大學附屬實驗中學 胡德林

☉江南大學附屬實驗中學 黃 靜

數(shù)學模型（數(shù)學模型：對于現(xiàn)實世界的一個特定對象，為了一個特定的目的，根據(jù)特有的內(nèi)在規(guī)律，做出一些必要的簡單假設，運用適當?shù)臄?shù)學工具，得到一個數(shù)學結(jié)構(gòu)）為我們提供了一種解決問題的方法和手段，一把開啟問題大門的鑰匙，它把數(shù)學和生活緊密聯(lián)系起來，使我們有了一雙發(fā)現(xiàn)生活中的數(shù)學的眼睛，是解決實際問題的一種有效工具，它的運用，讓我們感受到數(shù)學無處不在，感受到生活與數(shù)學息息相關.要能更好地學習和生活，我們必須學會數(shù)學的運用，培養(yǎng)應用能力.古人曰：“授人以漁，不如授人以漁”，我們要教會學生學習，教會學生學習的方法和解決問題的能力遠比教給學生知識更重要，模型的運用更好地體現(xiàn)了數(shù)學運用的廣泛性和靈活性，更有利于培養(yǎng)學生的應用能力.現(xiàn)就初中數(shù)學課本中出現(xiàn)的一個數(shù)學模型的運用，談談數(shù)學應用能力的培養(yǎng)策略.

原始模型問題呈現(xiàn)：

將軍飲馬問題：如圖1，據(jù)說，在古希臘有一位聰明過人的學者，名叫海倫.有一天，一位將軍向他請教了一個問題：從A地出發(fā)到河邊MN飲馬，然后回到B地，走什么樣的路線最短？如何確定飲馬的地點？

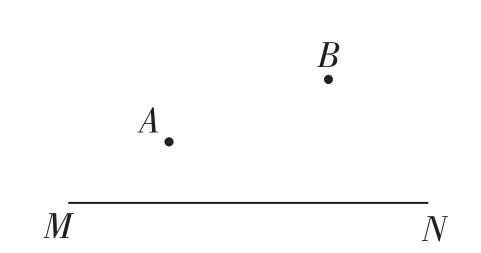
圖1

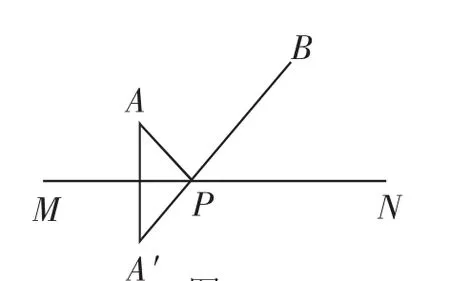
圖2

海倫給出的解決方法：如圖2，作點A關于直線MN的對稱點A′，連接A′B，交直線MN于點P，則P點所在位置即為將軍飲馬的地點.

應用能力培養(yǎng)策略1：教會學生閱讀和分析，弄清問題的本質(zhì)，提煉數(shù)學模型

上面的問題是一個實際問題，我們通過分析、梳理，發(fā)現(xiàn)其本質(zhì)就是關于兩個點和一條直線的問題，找出了關鍵的要素，就可以將它提煉成一個簡潔的數(shù)學模型.

這個問題模型可以提煉為：已知兩個定點A、B和一條定直線MN的問題.

通過這樣的提煉，建立起了如圖2所示的數(shù)學模型，學生更加容易理解、掌握和運用.

在教學過程中，通過引導學生對內(nèi)容進行認真細致的閱讀、理解、分析、領悟，弄清來龍去脈，抓住問題的本質(zhì)和關鍵，提煉出數(shù)學模型，做到一針見血.

應用能力培養(yǎng)策略2：教會學生總結(jié)和歸納，洞察問題的真相，掌握模型的變化

模型運用一：在平面圖形中的運用

（一）在三角形中的運用：與三角形的特殊性質(zhì)融合.

問題1：如圖3，在等邊△ABC中，AB=6，N為AB上一點，且AN=2，∠BAC的平分線AD交BC于點D，M是AD上的動點，連接BM、MN，則BM+MN的最小值是______.

圖3

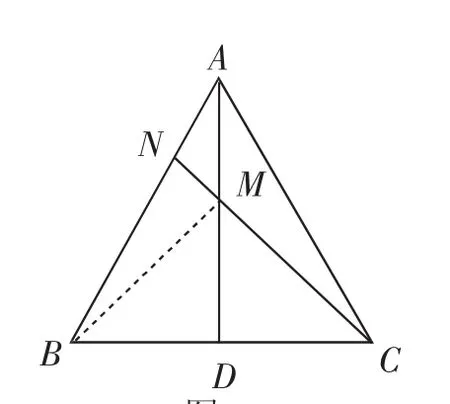
圖4

模型提煉：在這個問題中，B、N是兩個定點，AD是定線，要求在AD上確定一點M.

解決方法：如圖4，根據(jù)模型，根據(jù)等邊三角形的性質(zhì)，因為點B與點C關于AD對稱，所以只要連接CN，交AD于點M，此時M點就滿足BM+MN的值最小.（改變等邊三角形為等腰三角形，同樣可以這樣處理）

（二）在正方形中的運用：與正方形性質(zhì)的融合.

問題2：如圖5，E為正方形ABCD的邊AB上一點，AE=3，BE=1，P為AC上的動點，則PB+PE的最小值為______.

模型提煉：在這個問題中，B、E是兩個定點，AC是定線段，要求在AC上確定一點P.

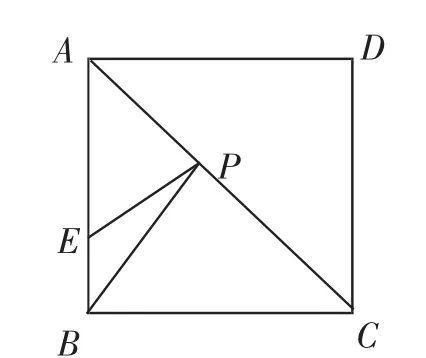
圖5

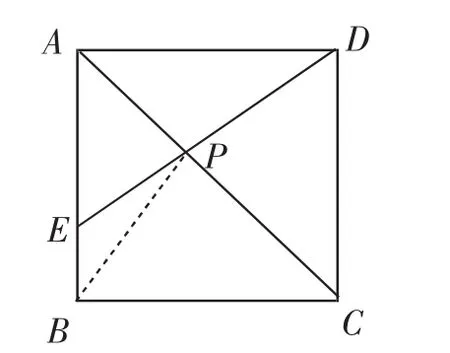
圖6

解決方法：如圖6，根據(jù)模型，因為點B與點D關于AC對稱，所以只要連接BD，交AC于點P，此時PB+PE的值最小.（此題中的正方形也可以改為矩形、菱形）

（三）在圓中的運用：與圓的性質(zhì)的融合.

問題3：如圖7，已知⊙O的直徑CD為2，弧BC的度數(shù)為60°，點A是弧BC的中點，在直徑CD上作出點P，使BP+AP的值最小，則BP+AP的最小值為______.

模型提煉：如圖7，在這個問題中，A、B是定圓⊙O上兩個定點，直徑CD是定線段，要求在線段CD上確定一點P，使BP+AP的值最小.

圖7

圖8

解決方法：如圖8，根據(jù)模型，只要過點A作AA′⊥直徑CD，交⊙O于點A′，則A′就是點A關于CD的對稱點，連接A′B，交CD于點P，此時點P就滿足BP+AP的值最小.

模型運用二：在函數(shù)圖像中的運用

（四）在一次函數(shù)中的運用：與坐標系的融合.

問題4：如圖9，已知兩點A（-1，3）、B（3，5），點P為x軸上一個動點.當PA+PB的值最小時，求點P的坐標.

模型抽取：在這個問題中，A、B是兩個定點，x軸是定直線，要求在x軸上確定一點P.

解決方法：如圖10，作點A（或B）關于x軸的對稱點A′（或B′），連接A′B（或B′A），交x軸于點P，此時P點就滿足PA+PB的值最小.

（五）在二次函數(shù)中的運用：與二次函數(shù)的性質(zhì)融合.

圖9

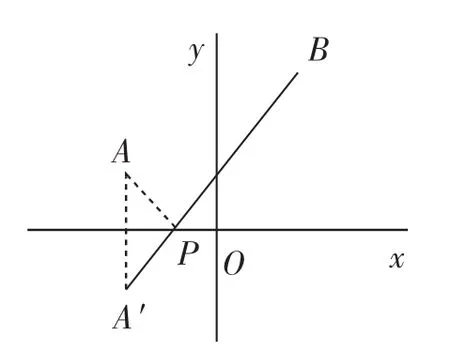
圖10

問題5：如圖11，拋物線y=ax2+bx+c的對稱軸為直線x=-3，該拋物線交x軸于A、B兩點，交y軸于點C（0，4），以AB為直徑的⊙M恰好經(jīng)過點C.

（1）求這條拋物線所對應的函數(shù)關系式.

（2）設⊙M與y軸的另一個交點為D，請在拋物線的對稱軸上求作一點E，使得△BDE的周長最短.

模型抽取：在本題第（2）問中，由于△BDE的周長=BD+BE+DE，而BD的長是定值，所以要使△BDE的周長最短，就是要使BE+DE最短，從而就轉(zhuǎn)化為模型問題.在這個模型中，B、D是兩個定點，拋物線的對稱軸是定直線，要求在對稱軸上確定一點E.

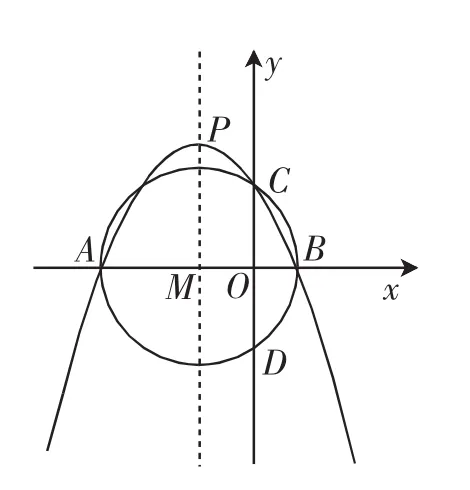
圖11

圖12

解決方法：如圖12，由拋物線的性質(zhì)，知點B關于拋物線的對稱軸的對稱點就是點A，所以連接AD交拋物線的對稱軸于點E，此時點E就滿足BE+DE最短，從而△BDE的周長也就最短.

上面的幾個問題展現(xiàn)了模型在不同的幾何圖形中以不同的變換形式呈現(xiàn)，但只要我們細心觀察，認真歸納總結(jié)，對情景進行梳理、對問題進行提煉，就能發(fā)現(xiàn)這些問題無非是給原始模型換上了不同的外衣，使模型出現(xiàn)在不同的場合中，“人還是那個人，物還是那個物”，只是不變中的變化，變化中的不變，萬變不離其宗，仍然是兩個定點和一條定直線的問題，達到了一通百通.

應用能力培養(yǎng)策略3：教會學生轉(zhuǎn)化思想，把握問題的本質(zhì)，突破模型的空間

模型運用三：在立體圖形中的運用：圓柱體中的運用與圓柱體性質(zhì)的融合

問題6：有一圓柱形食品盒，它的高等于16cm，底面直徑為20cm，螞蟻爬行的速度為2cm/s.

（1）如圖13，在盒內(nèi)下底面的A處有一只螞蟻，它想吃到盒內(nèi)對面中部點B處的食物，那么它至少需要多少時間？（盒的厚度和螞蟻的大小忽略不計，結(jié)果可含π）

圖13

圖14

（2）如圖14，在盒外下底面的A處有一只螞蟻，它想吃到盒內(nèi)對面中部點B處的食物，那么它至少需要多少時間？（盒的厚度和螞蟻的大小忽略不計，結(jié)果可含π）

模型提煉：此題的第（2）問只要將圓柱體沿側(cè)面展開（如圖15），問題就轉(zhuǎn)化為已知兩個定點A、B和定直線CD，在直線CD上找一點P，使得PA+PB最短.

解決辦法：如圖16，將圓柱體沿側(cè)面展開，得到長方形，其中A、B兩點是定點，線段CD是定線段，要求在CD上確定一點P，使PA+PB最短.所以對照模型很容易想到……

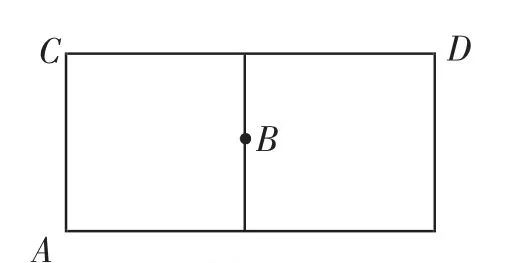
圖15

圖16

此問題看似與模型無關，模型是在平面圖形中的運用，而此問題是在立體圖形中的運用，但只要將圓柱體沿側(cè)面展開，就將立體圖形轉(zhuǎn)化成了平面圖形，呈現(xiàn)在我們面前的就是模型的真面目，揭開面紗就顯出了真相，只是模型的轉(zhuǎn)化而已，實現(xiàn)了舉一反三.

應用能力培養(yǎng)策略4：教會學生類比延伸，利用問題的聯(lián)系，實現(xiàn)模型的擴展

模型運用四：模型外延運用：類比推理、運用延伸

問題7：如圖17，臺球桌面上有如圖所示的母球A和紅球B，現(xiàn)要將母球A先擊打臺球桌面的邊沿CD后反彈擊中紅球B，畫圖說明擊打的線路.

模型提煉：此題與模型問題沒有本質(zhì)的區(qū)別，都是用對稱的方法解決，類比模型問題就能找到答案.

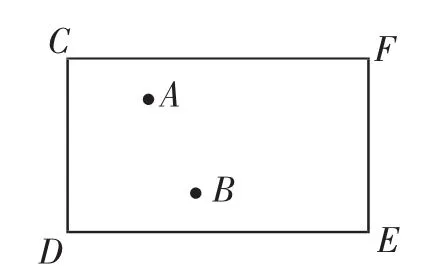
圖17

圖18

解決辦法：如圖18，作點A關于直線CD的對稱點A′，連接A′B，交直線CD于點P，則只要母球A擊打桌邊點P處，反彈后就會擊中目標紅球B.

此問題看似與模型不同，但通過將問題與模型進行對比，發(fā)現(xiàn)其與模型問題的本質(zhì)基本一樣，思想相同也相通，運用模型方法，輕易就將其解決.類比的思想、創(chuàng)新的延伸，使模型擴容，幫助我們解決了與之相近的問題，真正做到觸類旁通.

數(shù)學模型給我們提供了一種解決問題的方法和有效手段，學生在建模、觀模、用模和思模的過程中培養(yǎng)了：學習習慣、觀察視角、思考方法、思維方式、探索精神和創(chuàng)新能力，提高了數(shù)學應用能力，掌握了開啟數(shù)學問題的“鑰匙”，感受到了學習數(shù)學的輕松，收獲了學習數(shù)學的成功，體會到了學習數(shù)學的樂趣，增強了學習數(shù)學的信心，進而激發(fā)了學習數(shù)學的興趣、探究數(shù)學的熱情.W