以問題為“驅動”發展學生數學高階思維能力
——以“幾何最值問題”的專題探究為例

☉江蘇省江陰市敔山灣實驗學校 夏培培

本文以“幾何最值問題”專題課為例，以問題探究為驅動，帶領學生進行高階學習活動，組織學生經歷“操作—分析—交流—質疑—創造”的思維過程，使思維從低階向高階轉化，提升高階思維能力.

一、高階思維能力解讀

高階思維是指發生在高層次認知水平上的心智活動.它對應教學目標分類中諸如分析、綜合、評價等高層次認知水平的能力，是創新能力、問題解決能力、決策力和批判思維能力的核心［1］.

發展高階思維需要高階學習活動予以支持.高階學習是一種以學習者為中心、開展問題求解的學習活動，是一種形成知識共享、互動合作的學習方式.在“幾何最值問題”一節的教學中，筆者以探究為主線，以問題為依托，從基本模型入手，豐富問題背景，帶領學生從復雜圖形中發現基本模型并與相關思想方法聯系，進而拓展學生思維，培養學生的高階思維能力.

二、高階思維能力的實踐

教學環節1：根據問題情境回顧基本模型、思想方法

問題1：如圖1，已知直線l外兩點A、B，在l上找一點P，使PA+PB的值最小.

圖1

圖2

問題2：如圖2，已知∠MON外一點A，在OM、ON上分別找一點P、B，使PA+PB的值最小.

生1：對于問題1，以直線l為對稱軸作A（或B）的對稱點A′（或B′），連接A′B（或AB′）；對于問題2，過點A作AB⊥ON，交OM、ON于點P′、B′.

師：解決最值問題常用的方法是什么？

生2：軸對稱變換，旋轉變換，平移變換，確定動點軌跡等.

師：解決這兩個問題的理論依據是什么呢？

生3：兩點之間線段最短和垂線段最短.

設計意圖：問題是思維的起點和動力.通過兩個元問題帶領學生復習回顧解決最值問題的兩個基本模型，歸納最值問題的基本構造方法和理論依據.讓學生充分理解模型的內涵，并將知識和思想方法相聯系，豐富學生的知識結構.

教學環節2：拓展模型和思想方法，探尋思維發散點

問題3：如圖3，已知正方形OBCD，點A是OD邊上一定點，請你在對角線BD上確定一點P，使PB的值最小.

變式：如圖4，在l上找一點P，使得PB的值最小.

圖3

圖4

驅動性問題1：看到“你想到什么？能否從這個角度出發嘗試轉化

生4：我想到45°的三角函數值，構造直角三角形.

驅動性問題2：PB為直角邊還是斜邊？如何構造？

生5：由BD為對角線，得∠DBC=45°.以BP為斜邊構造直角三角形（如圖5）.

圖5

圖6

驅動性問題3：如果去掉正方形這一條件（如圖6），如何解決？

生6：補出BC這條線，按照剛才的方法.

學生畫圖探究解決并交流.

生7：在l下方構造Rt△BEP（如圖7），其中∠EBP=30°；找到點P′即為所求.

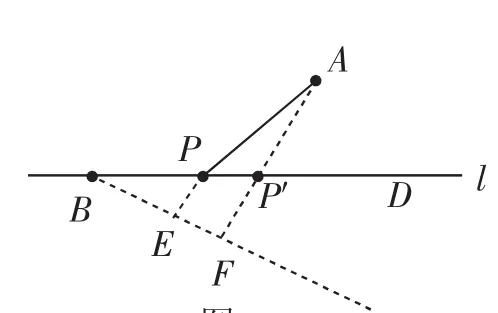
圖7

圖8

生8：能否在l上方構造Rt△BFP（如圖8，∠EBP=30°）？

驅動性問題4：不妨試一試，PA+PB=PA+PE.那么接下來就轉化為怎樣的問題？

生8：PA+PE的值最小，即將軍飲馬問題，作E點的對稱點，又變為圖7的方法.我明白了，因此在l上方構造，最終仍然要對稱轉化到l下方.

驅動性問題5：若將“PA+PB”改為“PA+k·PB”呢？

高階思維發展的關鍵是思維的交互、內省.思維不是自然發生的，但是它一定是由“難題和疑問”或“一些困惑、混淆或懷疑”引發的［2］.學生提出在直線上方構造直角三角形可否解決，此時引導學生進一步思考，發現問題轉化為將軍飲馬問題，需作對稱轉化到直線下方解決問題.在學生有想法和困惑時，教師予以肯定和支持，讓學生體驗解決問題方法的多角度、多樣性，在探究過程中進行思維的自我調節與省思，從而發展高階思維能力.

教學環節3：模型應用，產生質疑，進一步拓展模型

問題4：如圖9，在Rt△ABC中，∠ACB=90°，CB=4，CA=6，⊙C的半徑r為2，P為圓上一動點，連接AP、BP，求的最小值.

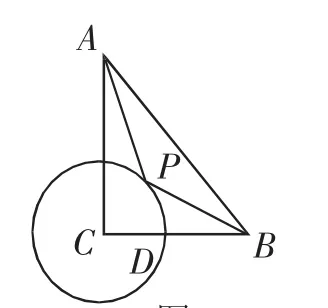
圖9

學生提出問題：經過探究發現利用三角函數值無法進行構造轉化BP.

驅動性問題6：函數值給我們提供了一個倍分關系，還有什么指示也能提供倍分關系呢？

生10：相似比，即構造相似三角形.

生11：CP=2，BC=4，它們存在2倍關系，由此構造△BCP的相似三角形，在BC上取點D，使CD=1，如圖10所示.由，∠PCD=∠PCB=45°，得△PCD △BCP，則則PD=，則

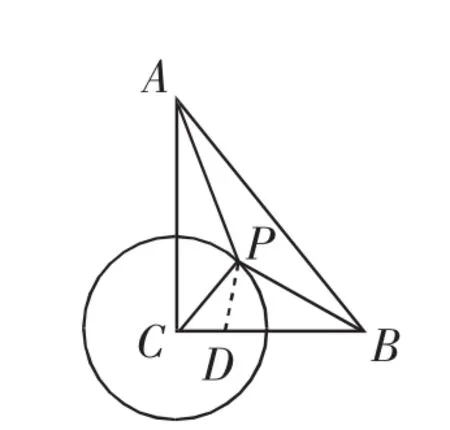
圖10

師：非常透徹，通過構造相似比再轉化邊，在構造相似三角形時需結合題中已知條件之間的關系.

設計意圖：利用三角函數轉化未能成功解決問題；由此引起認學生的認知沖突，教師充分利用沖突，引導學生打破思維定式、另辟蹊徑，探尋轉化倍分關系的另一種方法：相似三角形.構造相似三角形在學生思維過程中是一個“逆向”的過程，具有一定的挑戰性，教師有必要帶領學生一起探究構造方法，感悟構造過程，以此優化學生思維過程的內省與反思.該問題的設計旨在引導學生打破思維僵局，帶著質疑和批判去推理和思考，并給予學生充分的時間和機會探索和表達，在潛移默化中提高學生的數學思維品質，培養高階思維能力.

教學環節4：變式探究，創新優化

變式1：如圖9，在“問題4”的條件下，你會求BP的最小值嗎？

變式2：如圖11，已知扇形COD中，∠COD=90°，OC=6，OA=3，OB=5，點P是CD上一點，求2PA+PB的最小值.

圖11

設計意圖：課后研究是課堂的延伸，給出兩個變式讓學生在不同倍分關系和圖形環境中探究解決問題的策略，讓學生經歷知識、方法的再認識和再創造過程.

三、培養學生高階思維能力的教學思考

1.精心設計問題，培養幾何直觀

認知心理學認為，“問題”是思維活動進行的原動力和牽引力.問題的設計關系到學生思維的深度和廣度；教師的思維結構觀念也影響著學生圖形與幾何的學習走向和效果.因此教師在備課時，要根據學生當前的認知結構，認真研讀教材，把握知識體系，關注知識和方法的形成過程及學生的學習心理圖式，從而精心設計新知識的“邏輯關聯點”，引導學生自我構建知識網絡，提升圖形與結合思維結構水平，促使學生高階思維能力逐級躍升.

2.關注策略的形成，加強方法的積累

在解決問題的過程中，需重視解題策略的形成，關注問題的解法和結論.策略的學習無法通過直接的傳輸獲得，需要學生在畫圖、操作、猜想、實踐中發現問題、提出問題、分析和解決問題，從而總結、反思，提煉相應的方法、技巧、經驗，真正形成解決問題的策略.當然，策略的形成離不開方法的支撐，方法不是指一個特定的解題技巧，而是解決一類問題的通性通法，它在解決問題的過程中發揮著不可替代的作用.實踐證明，通過策略培養、方法養成積累的數學能力更利于學生的思維生長.

3.學會等待，靜待花開

在專題課的教學過程中，教師要舍得留時間給學生大膽嘗試，找到問題的核心所在.探究嘗試的過程，就是發展思維的過程.解決問題后也應留時間讓學生進行反思，將探究經驗內化為自己的數學素養.內化的過程，就是自我提升的過程.專題課的著眼點應放在學生學習能力發展上，讓學生通過課堂學習，創新數學思維方式，積累解決問題的方法，提升優化意識.

當然，數學思維能力的培養不是一蹴而就的，這需要教師在平時的教學過程中摒棄傳統的“授受”模式，為學生思維獨立性和創新性培養創造條件，使學生的潛能和創造性得到發揮，以期提高其高階思維能力.