光滑雙向漸進結構優化法拓撲優化連續體結構頻率和動剛度

滕曉艷，毛炳坤，江旭東

（1. 哈爾濱工程大學機電工程學院，哈爾濱 150001；2. 哈爾濱理工大學機械動力工程學院，哈爾濱 150080）

0 引 言

結構拓撲優化設計通過尋求在滿足性能最優條件下，結構材料在設計空間中沿最佳傳力路徑布局的拓撲形式。近三十年來，形成了許多基于梯度或啟發式的拓撲優化方法，主要包括變密度法、均勻化法、變邊界法（水平集法和相場法）以及漸進結構優化方法（evolutionary structural optimization, ESO）等[1-3]。

ESO法最初由Xie和Steven提出，基于生物進化思想，利用單元靈敏度信息逐漸刪除低效單元，從而得到優化的拓撲結構[4]。雙向漸進結構優化方法（bi-directional evolutionary structural optimization, BESO）繼承了ESO法的進化思想，不但可以刪除結構的低效單元，還可以在結構中需要的部位添加高效單元，BESO方法在結構應力、靜剛度、頻率、屈曲以及依附性載荷問題方面得到了廣泛的應用[5]。但是，Zhou等[6]指出ESO法的進化準則導致方法存在單元過刪除問題，通過端部彈性支撐的懸臂梁結構的優化問題的求解失效驗證了方法存在的理論缺陷。盡管Huang等[7]通過細密網格和設置較低進化率解決了上述測試模型的優化問題，但是由此也表明 ESO法或 BESO法的進化準則存在網格的強依賴性問題，可能導致優化失敗或非最優解。賀丹等[8]認為單元相對密度較大的進化步長可能引起較大的靈敏度誤差，導致進化準則的失效。匡兵等[9]根據靈敏度信息評價單元對結構性能的影響，建立單元相對密度進化步長的控制模型以調諧單元的刪除率和添加率，以避免由于誤刪單元導致優化失敗。Valerio等[10-12]提出了一種基于軟殺策略的光滑漸進結構優化（smooth evolutionary structural optimization,SESO）方法，根據單元對結構性能的貢獻調整單元剛度，控制低效單元在結構進化過程中逐漸被刪除，有效解決了結構的強度、靜剛度以及多約束優化問題。

結構動力學拓撲優化包括 2類設計問題：結構動力特性（固有頻率）優化和結構動力響應（振動激勵下結構的位移、速度、加速度、應力和應變能等）優化。動力特性拓撲優化主要是通過提高結構的低階固有頻率來避開外部激勵頻率，其最終目的仍然是為了實現結構動力響應優化。結構動力學優化涉及靈敏度計算、動響應分析以及約束函數處理等方面的問題，優化算法需要反復計算結構響應對設計變量的偏導數，對于大規模與多變量結構的動力學優化問題，所消耗的計算資源往往是難以承受的[13-16]。為了有效減小結構動力學優化過程的求解規模，Park等[17]提出等效靜載荷法（equivalent static loads, ESL）將動力學優化問題轉化為靜力學多工況優化問題，利用結構線性優化技術求解動態線性優化問題。Stolpe[18]通過數學規劃法證明了ESL法滿足KKT優化準則，從數學上驗證了優化方法的有效性。Jang等[19]基于ESL法，以降低結構峰值響應為目標，研究了不同載荷特征以及動態多工況問題的動力學拓撲優化方法。Kim等[20-21]為了縮減結構動力學優化規模，將自由度縮聚方法或模型降階技術與結構線性靜態優化技術相融合，研究了基于系統縮減方法的ESL動力響應優化問題。陳濤等[22-23]針對ESL法求解結構動態非線性優化問題收斂效率低的問題，結合靜態線性優化方法與最速下降法提出了ESL梯度優化方法，解決了汽車正面碰撞關鍵結構優化設計問題。高云凱等[24-26]將ESL與變密度法相融合，求解了結構非線性動力學拓撲優化問題；但是，低密度單元的局部偽模態和網格畸變使優化過程難于收斂。

綜上，SESO的光滑漸進優化策略能夠有效抑制低效單元的過刪除問題，同時采用的軟殺策略亦可避免低密度單元的局部偽模態和網格畸變等奇異性問題。由此，本文以SESO靜力學拓撲優化為基礎，提出光滑雙向漸進結構優化方法（smooth bi-directional evolutionary structural optimization, SBESO），求解連續結構的頻率和動剛度動力學拓撲優化問題。以結構固有頻率最大化為目標，構建基于SBESO法的頻率優化模型。研究SBESO算法參數對收斂性及優化解的影響。以結構動剛度最大化為目標，融合等效靜載荷法（ESL）與光滑雙向漸進結構優化方法（SBESO），提出動載荷作用下的結構動剛度優化方法。

1 光滑雙向漸進結構優化方法

基于漸進結構優化方法，結構動力學拓撲優化的數學模型表述如下

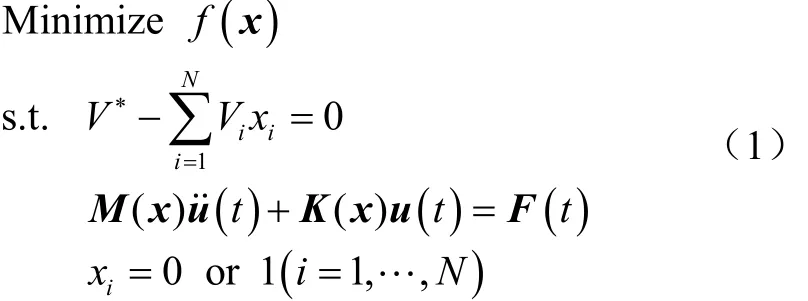
對于傳統的BESO方法，通過式(1)的梯度信息評價添加/刪除單元對目標函數變化量的影響，根據濾波后的靈敏度信息和體積約束確定當前設計域中同時添加的單元集和刪除的單元集，相應的漸進優化準則為

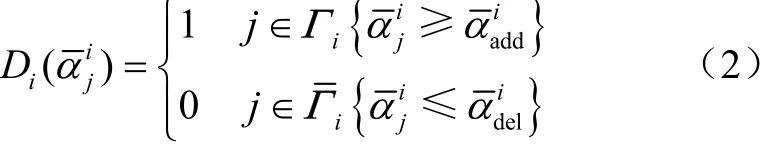
傳統 BESO方法中，較大的單元相對密度的進化步長，導致利用目標函數梯度信息確定結構低效單元可能引起較大的系統誤差，引起非低效單元的誤刪除問題，最終將造成優化失敗或得不到最優解。由此，將式(2)中的單元靈敏度按升序排列，中刪除率q的單元集將被刪除，中1-q的單元集將返回設計域。此外，ΓGS中的單元特性-質量矩陣和剛度矩陣通過權重函數更新返回設計域（如圖 1 所示）。光滑雙向漸進結構優化準則及流程圖見圖1和圖2。上述方法即為光滑雙向漸進結構優化（smooth bi-directional evolutionary structural optimization, SBESO）方法，相應的光滑漸進優化準則為

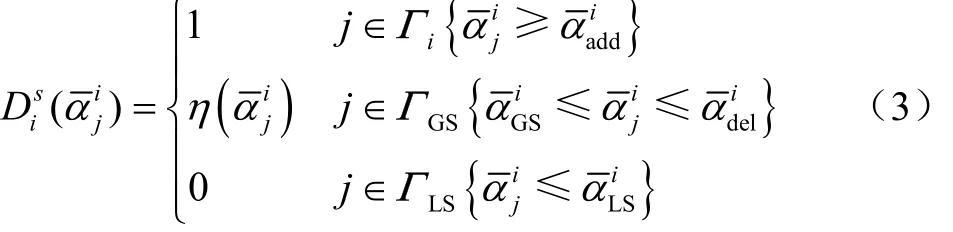
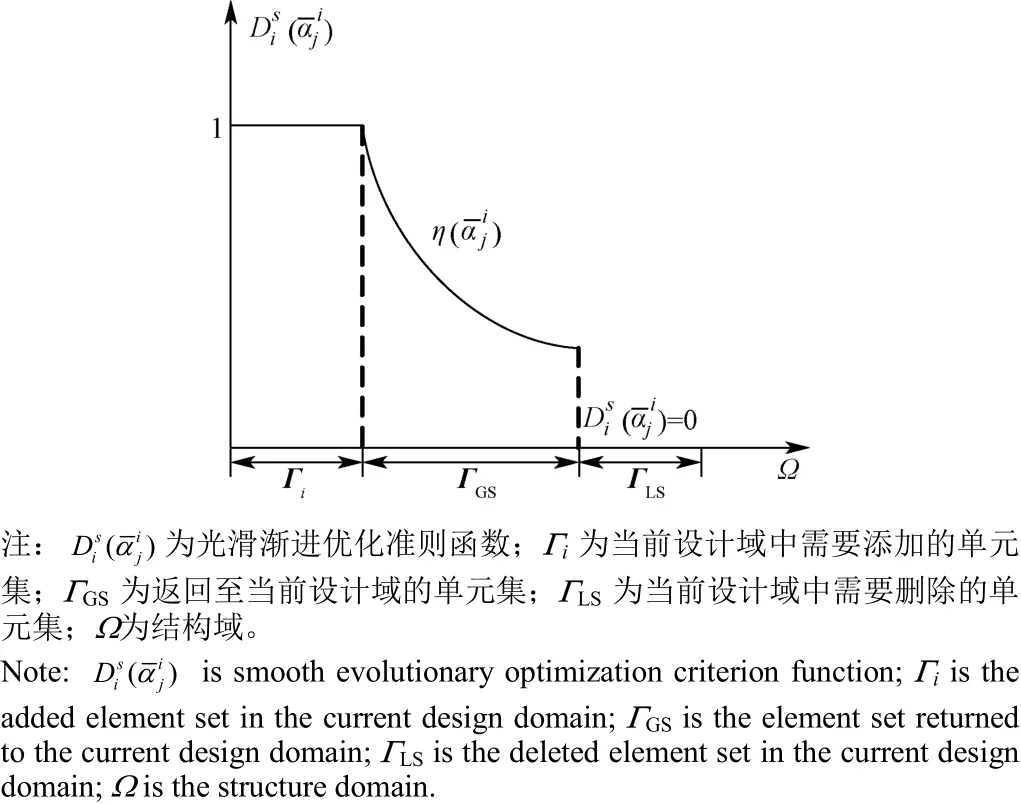
圖1 光滑雙向漸進結構優化法的漸進優化準則Fig.1 Evolutionary optimization criterion of smooth bi-directional evolutionary structural optimization method

對于SBESO方法，根據式（3），結構在第i次優化迭代中設計域中單元j的質量與剛度矩陣分別為

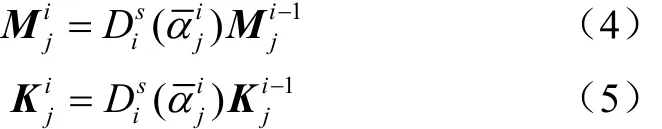
由式（4）與式（5）可以看出，權重函數根據單元對結構性能的貢獻調節單元質量與剛度矩陣，能夠保證低效單元的質量與剛度在優化迭代中逐漸趨向于0，進而從結構設計域中漸進刪除。因此，SBESO方法通過引進權重函數和控制單元刪除率可以有效抑制單元過刪除問題，提高漸進優化方法的尋優能力。

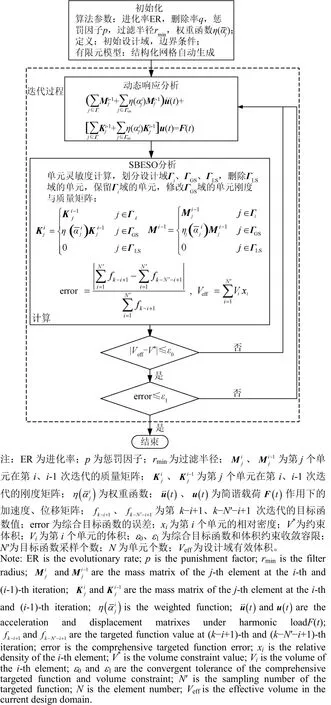
圖2 SBESO方法優化流程Fig.2 Optimal procedure of SBESO

根據 SBESO法的漸進優化準則，如果刪除率q=100%，則SBESO方法退化為傳統的BESO方法，由此式（4）、式（5）退化為

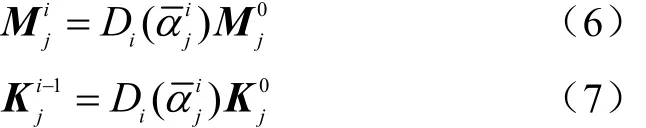
基于經典有限元理論，結構動力學控制方程為

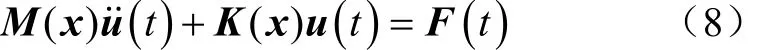
將式（6）與式（7）代入式（8）中，得到優化結構當前設計域的動力學控制方程為

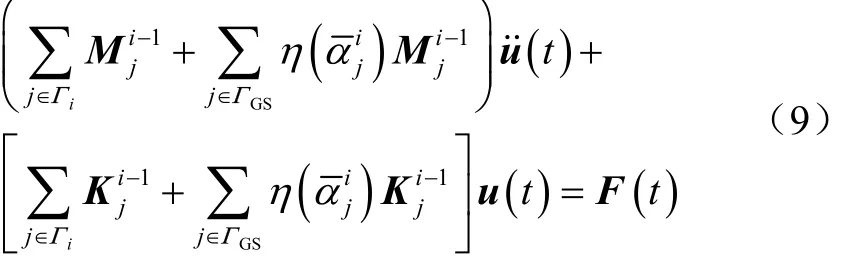
結構進化過程中在達到體積約束后，目標函數仍需滿足如下收斂準則

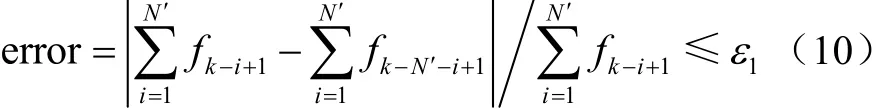
式中 error為綜合目標函數的誤差，k為當前迭代數，ε1為收斂容差，N′為整數，在第迭代步的值。圖2闡明了基于光滑雙向漸進結構優化方法的優化流程。

由圖2可知，則SBESO優化步驟如下所述：1）設置SBESO的刪除率q、進化率ER、目標體積V*、單元靈敏度過濾半徑 rmin、權重函數等算法參數，利用有限元網格離散初始設計域；2）定義位移邊界約束條件和載荷，對結構進行有限元分析，計算所有單元的靈敏度；3）按照靈敏度的大小設置閥值，按照閥值把所有單元劃分為3個區域Γi，ΓGS，ΓLS；4）向當前設計域中添加Γi區域中的單元，完全移除ΓLS區域中的單元，按照權重函數η（）修改Γ 區域內的單元質量與剛度矩陣；5）重復GS步驟 2）～4），直至在結構同時達到目標體積和滿足收斂準則時終止優化過程。

2 頻率優化

2.1 數學模型

以結構l階固有頻率最大為目標，則基于SBESO方法的結構頻率優化模型表述為

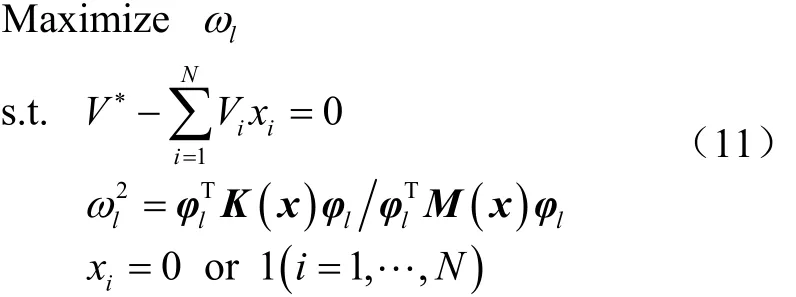
式中ωl為結構l階固有頻率，φl為結構l階歸一化振型。

對于無阻尼振動系統，優化結構的固有頻率可表示為Rayleigh商形式，則有

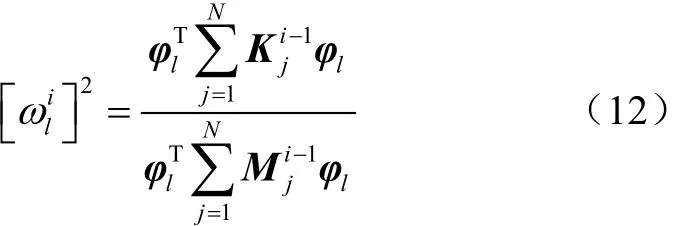
通過式（12）計算目標頻率對設計變量的偏導數，得到單元的靈敏度，表示為

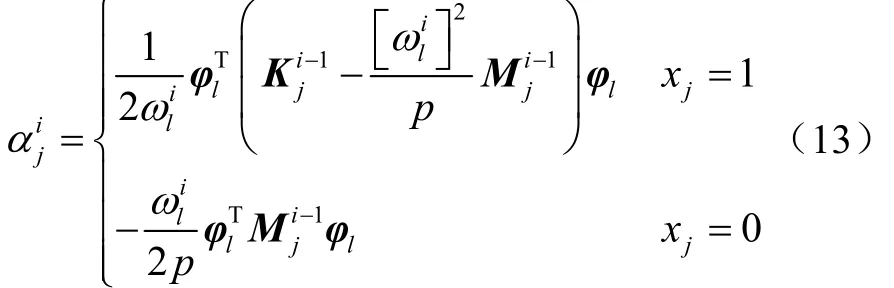
由此，聯立式（13）、式（4）和式（5），解算結構頻率靈敏度。結合頻率梯度信息，根據單元進化準則，對低效單元進行刪除。

2.2 數值算例

以兩端簡支薄板結構的一階固有頻率最大化為優化目標，目標體積為總體積的 50%。薄板結構初始設計域的幾何尺寸為240 mm×30 mm（如圖3所示），材料的楊氏模量為 E=10 GPa，泊松比為 μ=0.3，材料的密度ρ=1×103kg/m3。利用 4節點雙線性平面應力單元將結構設計域劃分為240×30個單元，采用的權重函數為線性函數，SBESO算法參數為：刪除率q=40%～100%，ε1=0.02，靈敏度過濾半徑rmin=5 mm，懲罰因子p=3。

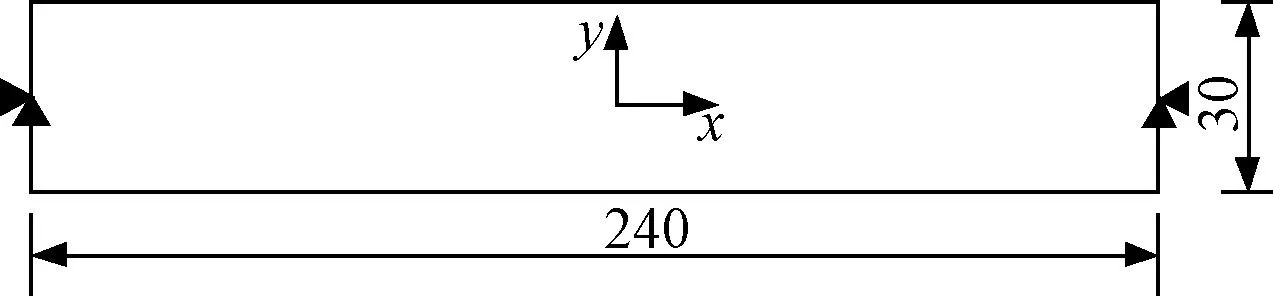
圖3 兩端簡支薄板結構示意圖Fig.3 Schematic diagram of plate simply supported along both ends

BESO方法與SBESO方法優化后的頻率幾乎相等，2種方法的頻率值均隨迭代過程單調增加（除躍變點外），漸進收斂到最優值（如圖4所示）。對于BESO方法，單元過刪除（刪除率q=100%）引起優化過程中的結構拓撲的不連續，進而形成頻率值在迭代過程中躍變為零頻率的現象。對于SBESO方法，隨著刪除率的降低（刪除率 q=70%～40%），誤刪除的低效單元逐漸減少，致使迭代過程中頻率值的躍變現象隨著單元刪除率的減少逐漸得到抑制；同時，結構拓撲優化構形與也隨單元刪除率的減少逐漸逼近于同一構形。

圖4 刪除率q對頻率優化拓撲與收斂過程的影響Fig.4 Effect of deletion rate q on optimal topology of frequency and corresponding process

對比分析權重函數（常函數、線性函數和正弦函）的光滑性對 SBESO結構優化拓撲構形及收斂過程的影響。由于常函數權重函數的光滑性最差，致使單元過刪除的抑制效果不顯著和頻率值躍變現象的存在，SBESO優化拓撲構形（圖5b所示）接近于BESO方法的優化結果（圖4a所示）。但是，線性和正弦權重函數的光滑性顯著增強，有效抑制了單元過刪除問題，致使低效單元逐漸被刪除和迭代過程更光滑，均收斂于同一最優拓撲結構（圖4d和5a所示）。由此，采用線性和正弦權重函數更有利于獲得結構最優拓撲解。

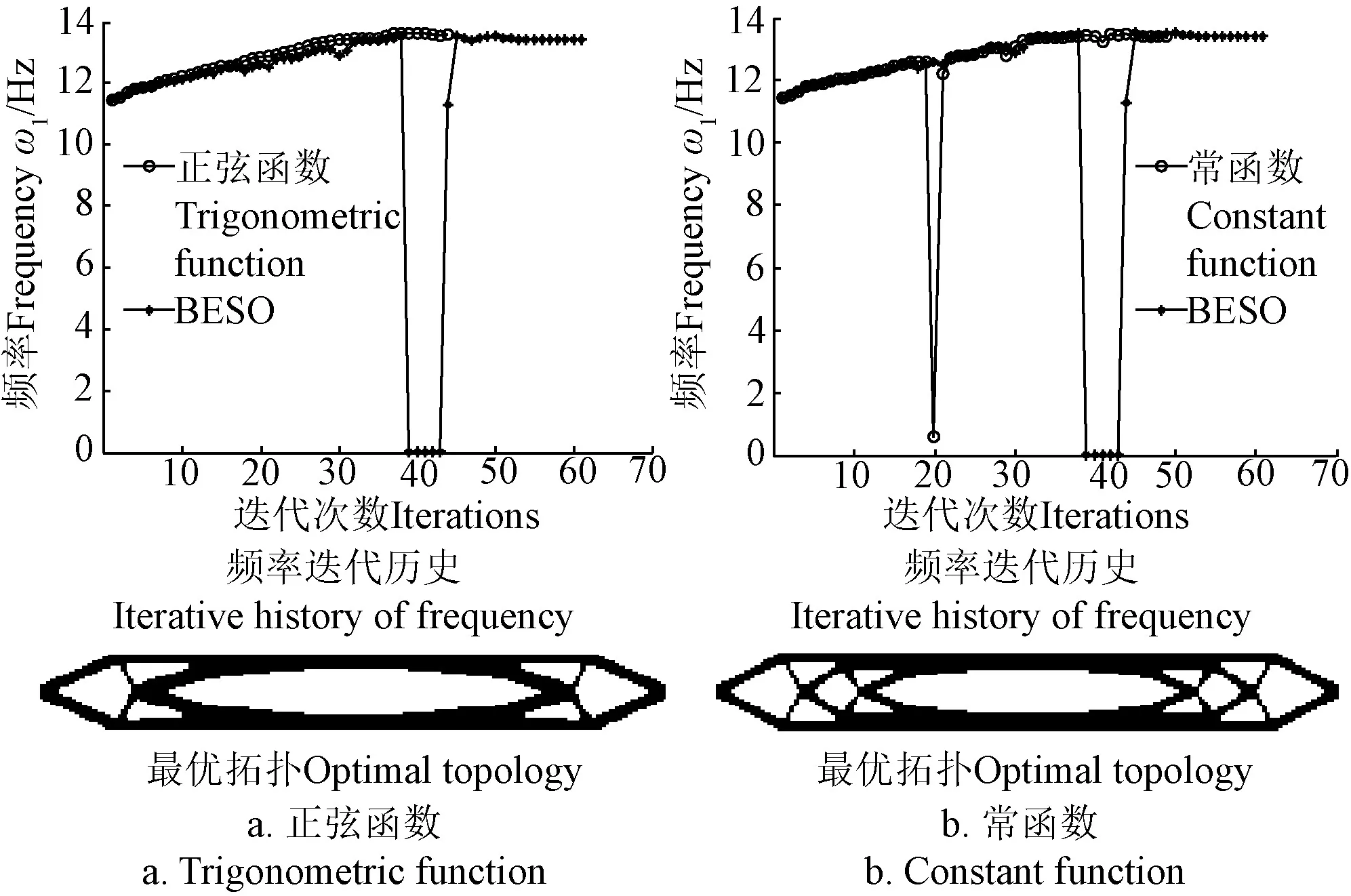
圖5 不同權重函數對優化拓撲與收斂過程的影響(q=40%)Fig.5 Effect of weight function on optimal topology and corresponding process (q=40%)

3 動剛度優化

3.1 數學模型

動剛度優化作為結構動力響應優化問題，旨在降低結構在振動激勵下的應變能來實現結構的動力性能優化。由于結構動柔度（即應變能）是全局剛度的逆測度，因此，動載荷作用下結構動剛度優化數學模型表述如下[25]

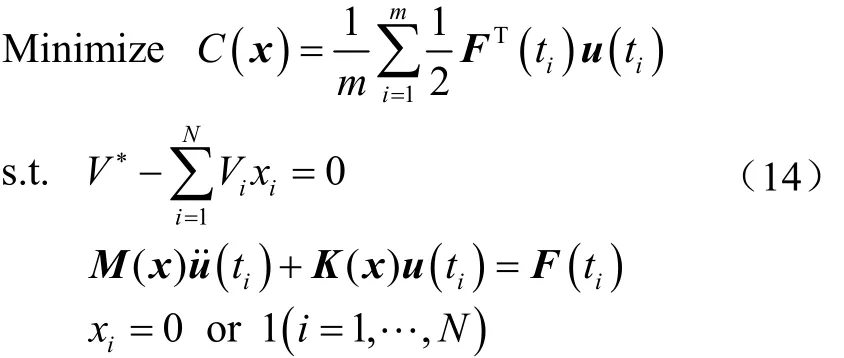
式中常數m表示總時間步。對于式(14)表述的大規模的結構動力學拓撲優化問題，傳統的基于梯度的優化算法需要反復計算結構動響應和約束函數對設計變量的偏導數，而啟發式優化算法不需要目標函數和約束函數的梯度信息，但需要計算函數值，從而不可避免地進行大規模結構分析，上述2種方法使得計算資源的消耗是難以承受的。

等效靜載荷法的優化過程由分析域（外層循環）和設計域（內層循環）組成（如圖 6所示）。分析域進行結構動態響應分析，得到結構各時間步的位移場；設計域根據位移響應計算等效靜載荷，按時間步將等效靜載荷處理為多載荷工況，實施線性靜態優化，然后更新設計變量返回到設計域重新計算。

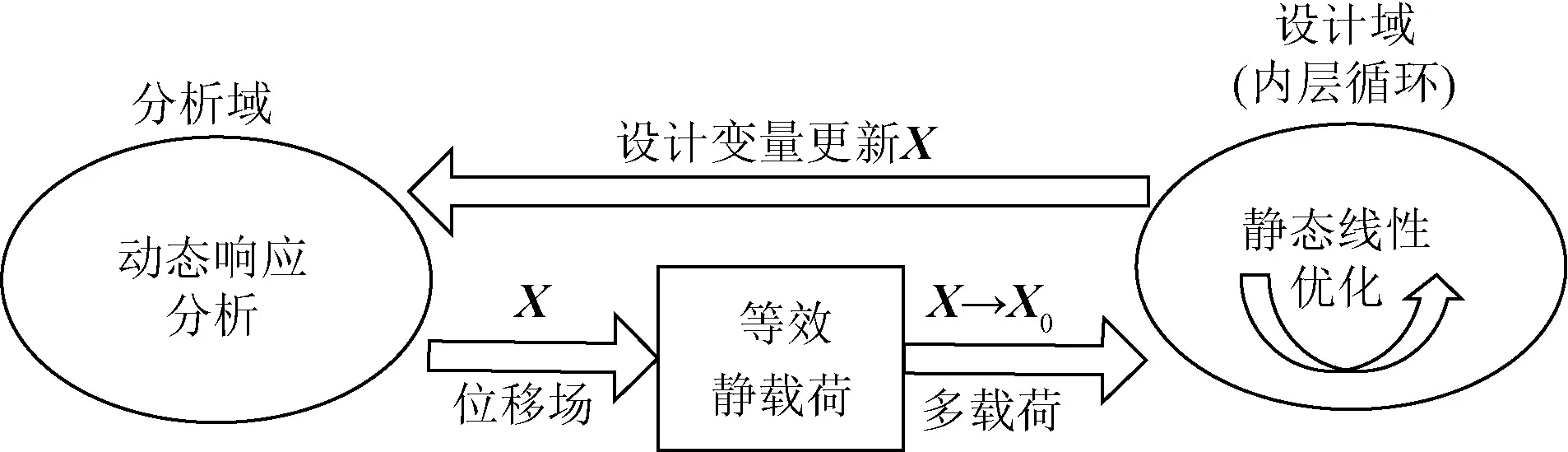
圖6 等效靜載荷法的基本思想Fig.6 Fundamental principle of equivalent static loads method

在內層循環的第一次迭代中，結構初始靜態位移場與動態響應分析的位移場是完全相同的。通過式（9），可以確定任一時間步的動態位移場 ()t*u ，則基于位移場等效原理獲得等效靜載荷eq()t*f

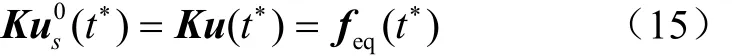
對于無阻尼振動系統，系統的特征方程表示為

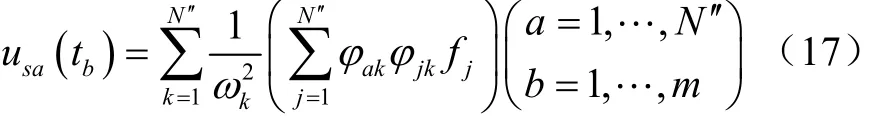
盡管式（17）可精確計算結構的等效靜載荷，但是，它需要完成模態分析和非常昂貴的瞬態分析以及代數方程組計算。因此，為了減少動響應問題的計算規模，通過一種等效靜載荷的近似計算方法，將等效靜載荷僅施加于實際動載荷作用的附近區域節點，即假設等效靜載荷存在如下l個非零分量，則有

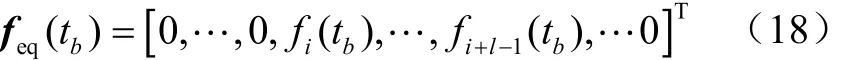
將式（18）代入式（17），則有

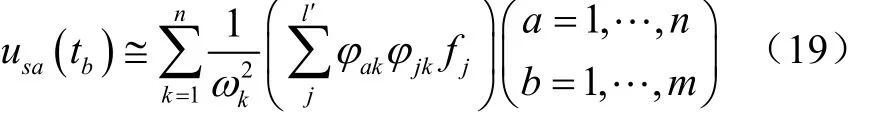
因此，基于等效靜載荷法，則式(14)描述的結構動剛度優化模型轉化為靜態線性多工況剛度優化模型，則有

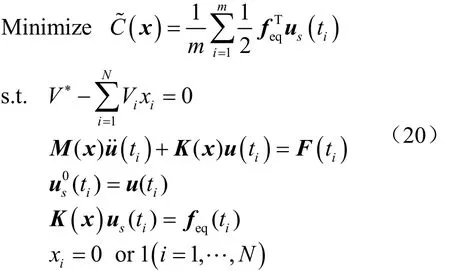
基于SBESO方法，結合靜態線性多工況剛度優化模型的靈敏度計算，得到式（20）的靈敏度計算公式，表示為

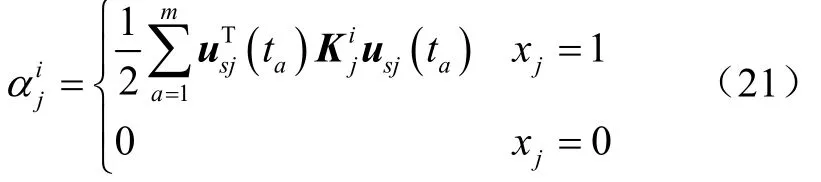
為了保證單元相對密度在優化過程中的收斂性，定義單元相對密度的收斂準則

結合 ESL方法和 SBESO方法，提出連續體結構動剛度優化算法。主要優化流程如下：1）設置優化算法參數與初始設計變量，定義結構初始設計域的幾何形式、外載荷與位移邊界條件，建立結構的動態分析有限元模型；2）基于位移場等效原理，利用式（15）解算結構在外部激振力作用下的等效靜載荷，按時間步將等效靜載荷處理為多工步外載荷，根據式（21）計算單元靈敏度，進行靜態線性多工況剛度優化；3）根據靜態線性優化結果更新設計變量，按照式（4）和式（5）返回單元質量與剛度矩陣。重復上述步驟，直到最后剩余單元同時滿足體積約束以及式（10）和式（22）的收斂準則。

3.2 數值算例

以一端固定薄板結構的動剛度最大化為優化目標，目標體積為總體積的 50%。薄板結構初始設計域的幾何尺寸為120 mm×30 mm，右端承受簡諧載荷 ()ft~ 的作用（如圖7所示）。材料的楊氏模量為E=2 GPa，泊松比為μ=0.3，材料的密度ρ=4.8×103kg/m3。利用4節點雙線性平面應力單元將結構設計域劃分為120×30個單元，采用的權重函數為線性函數，SBESO算法參數為：刪除率q=60%～100%，error=0.02，靈敏度過濾半徑rmin=3 mm，懲罰因子p=3。

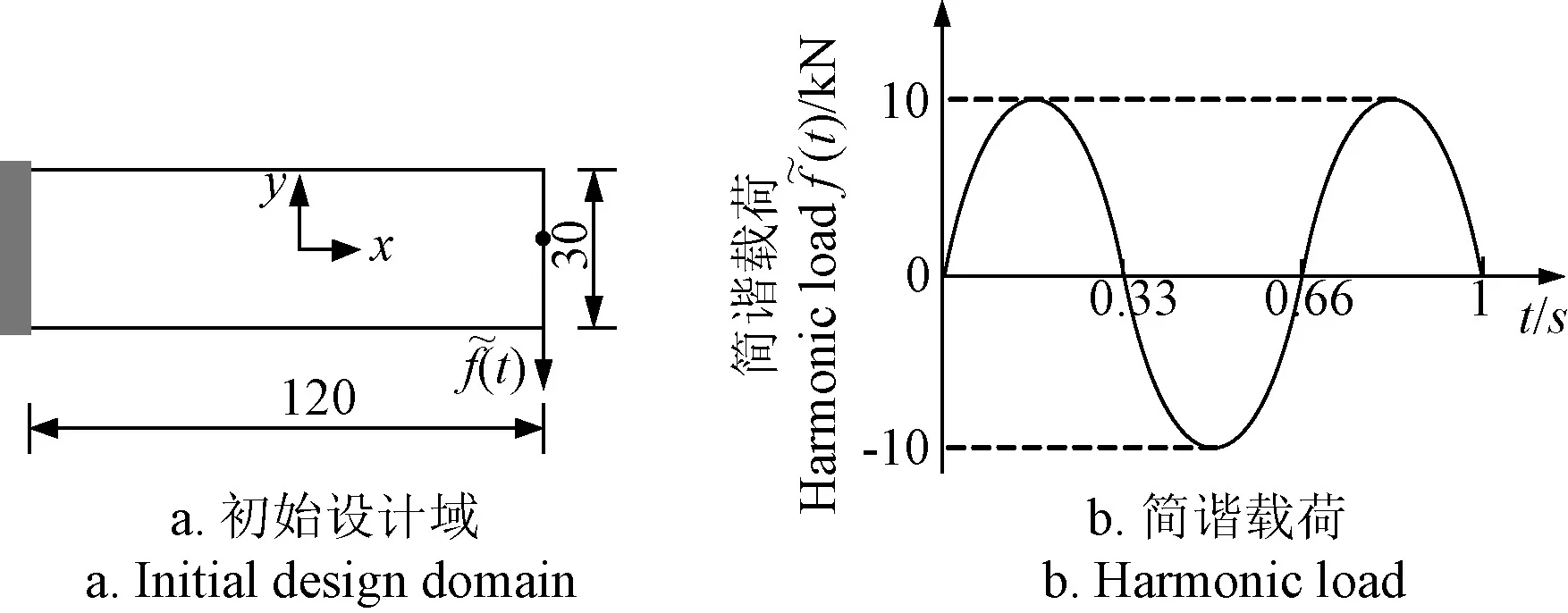
圖7 薄板結構的動剛度拓撲優化Fig.7 Topology optimization of dynamic stiffness of thin plate

BESO方法與SBESO方法優化后的動柔順度幾乎相等，2種方法均漸進收斂到最優值（如圖8所示）。

對于BESO方法，單元過刪除（刪除率q=100%）問題致使部分非低效單元在迭代過程中誤刪除，并且無法有效控制低效單元在優化過程中逐漸被刪除，拓撲構形可能陷入某一低效最優解，優化構形的邊界比較粗糙；而對于SBESO方法，能夠控制低效單元在優化過程中質量與剛度逐漸趨向于0，進而從設計域中逐漸刪除，同時使得迭代過程中結構拓撲優化構形隨單元刪除率的減少其結構邊界逐漸光滑，而且逼近于同一構形。

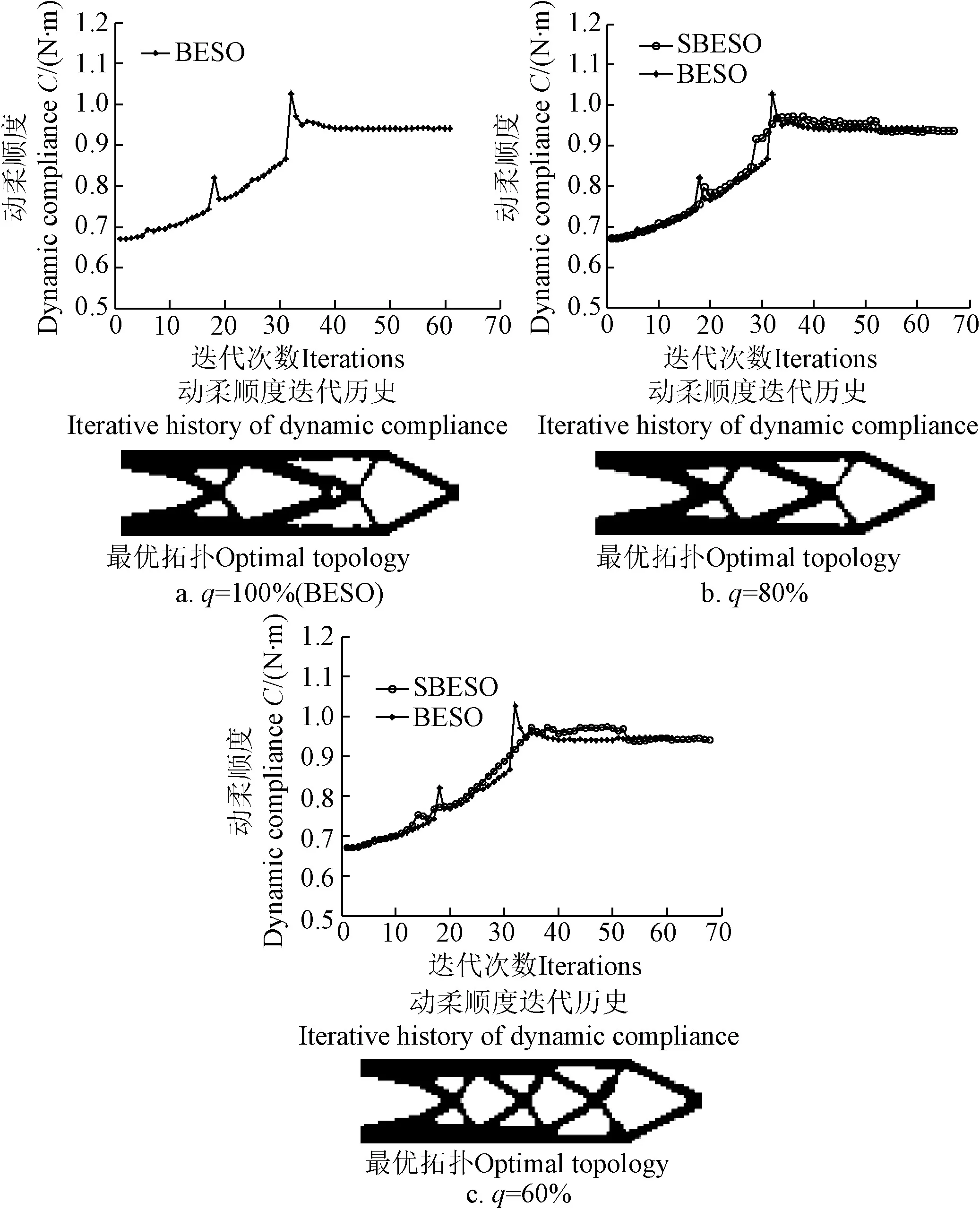
圖8 刪除率q對動剛度優化拓撲與收斂過程的影響Fig.8 Effect of deletion rate q on optimal topology of dynamic stiffness and corresponding process

4 結 論

針對 BESO方法的單元過刪除問題，提出一種低效單元的光滑刪除策略，求解了結構頻率優化和動剛度優化問題，獲得了如下研究結論：

1）研究了一種基于光滑雙向漸進結構優化（smooth bi-directional evolutionary structural optimization, SBESO）方法的結構動力學拓撲優化方法。與雙向漸進結構優化（bi-directional evolutionary structural optimization, BESO）方法相比，SBESO方法可以調節單元刪除率和權重函數，控制低效單元在結構設計域中逐漸被刪除，有效抑制了單元的過刪除問題，其優化算法具有一定的魯棒性和適應性。

2）提出了一種基于 SBESO方法的頻率優化方法。SBESO方法與BESO方法優化后的頻率幾乎相等，但是前者隨著單元刪除率的減少使結構拓撲優化構形逐漸逼近于同一構形。對比分析了權重函數（常函數、線性函數和正弦函）的光滑性對結構優化的影響，線性函數和正弦函數的光滑性強于常函數，致使迭代過程更加光滑，均收斂于同一最優拓撲結構。由此，采用線性和正弦權重函數更有利于獲得結構最優拓撲解。

3）將等效靜載荷方法與 SBESO方法相融合，提出動載荷作用下結構的動剛度優化方法。能夠控制低效單元在優化過程中質量與剛度逐漸趨向于零，進而從設計域中逐漸被刪除，同時使得迭代過程中結構拓撲優化構形隨單元刪除率的減少其結構邊界逐漸光滑，而且逼近于同一構形。

因此，本文提出的SBESO方法抑制了BESO方法的過刪除問題，進一步完善了 BESO方法的優化準則，對于解決連續體結構動力學優化設計問題具有較為重要的理論意義。