指示變量隨機缺失下變系數模型的分位數回歸
寧黎明,何曉霞,王志明
(武漢科技大學理學院,湖北 武漢,430065)
刪失數據廣泛存在于金融、生物、醫(yī)學、工程等研究領域。為了更好地對刪失數據進行分析,各種統(tǒng)計模型相繼出現,較早的有Cox提出的比例風險模型[1],但其中一些假設在現實中是不成立的。隨后Cox等[2]又提出了加速失效時間(accelerated failure time, AFT)模型:logT=XTβ+ε,將失效時間的對數表示為協(xié)變量的線性組合。AFT模型很顯然是有意義的,但在實際應用中,不可能保證所有協(xié)變量對生存時間都有線性影響,因此研究人員又提出了部分線性變系數模型,它在線性回歸模型的基礎上增加了非線性部分,使得整個模型具有更強的可塑性,通常采用局部多項式和光滑樣條來估計其非參數部分。基于局部多項式方法,Zhang等[3]研究了半變系數模型,而Fan等[4]研究了協(xié)變量帶測量誤差情況下的懲罰經驗似然估計。Zhao等[5]基于B樣條估計,得到半參數部分線性變系數模型的模態(tài)回歸。
分位數回歸較普通的均值回歸更加靈活,其應用也得到了迅速發(fā)展。何曉霞等[6]針對右刪失數據,得到光滑回歸函數的組合分位數回歸估計。Wang等[7]對非參數部分采用B樣條近似,得到部分線性變系數模型在縱向數據情形下的分位數回歸。Shen等[8]運用局部多項式方法,在指示變量缺失的條件下得到部分線性變系數模型的分位數回歸估計。由于局部多項式的計算速度較慢,因此本文采用B樣條估計,研究刪失指示變量缺失情形下部分線性變系數模型的分位數回歸。
1 模型描述
本文考慮右刪失數據情形下的部分線性模型
(1)

由于數據右刪失,故只能觀察到(Xi,Ui,Zi,Yi),其中Yi=min(Ti,Ci),Ci是隨機刪失時間。定義刪失指示量δi=I(Ti≤Ci)以及缺失指示量ξi,其中I為示性函數,如果δi被觀測到存在缺失時ξi=1,否則ξi=0。另外,記Hi=(Xi,Zi,Ui)。
2 估計方法和主要結論
2.1 樣條近似和估計
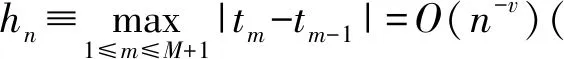
(1)s限制在任何區(qū)間IMi(0≤i≤M)上是r次多項式;
(2)對r≥2,s在區(qū)間[a,b]上是r次連續(xù)可微的。
由文獻[10],對Sn存在標準化的B樣條基{Bω,1≤ω≤mn},其中mn=M+r是Sn的維數。因此對于任意函數αn(t)∈Sn,能夠得到
(2)
在合理的平滑假設條件下,可以通過Sn中的基函數來逼近任意平滑函數。因此模型(1)中對α*的估計就可以轉化為估計αω。
(3)
進一步地,式(3)又可以寫為
(4)
其中Wi=Ip?B(Ui)·Xi且γ=(α1,α2,…,αmn)T,cτk是誤差ε的τk分位數。
(5)
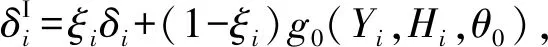
(6)
在刪失指示量隨機缺失的情況下,對于G(·)的估計不能再使用較為常見的Kaplan-Meier估計。參照文獻[11],這里給出G(·)的估計:
(7)
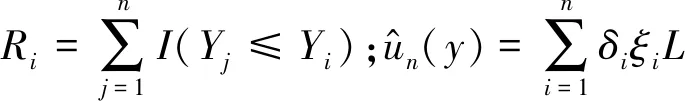
(8)
2.2 估計量的理論性質
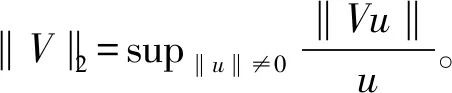
為了分析估計量的理論性質,首先給出以下假設條件:
(C1) 對于任意α*∈Ψ,有E[α*(Ui)]=0。
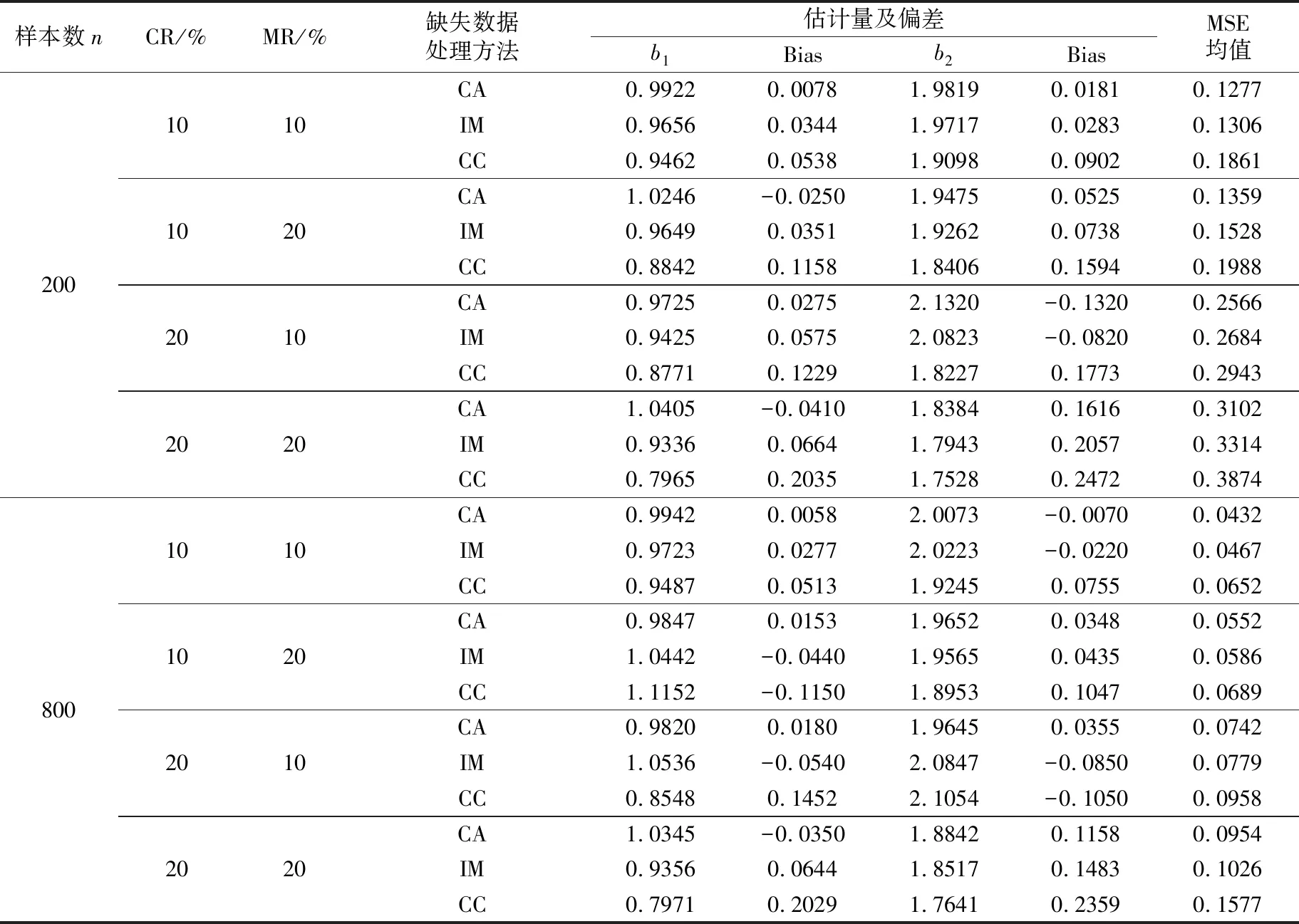
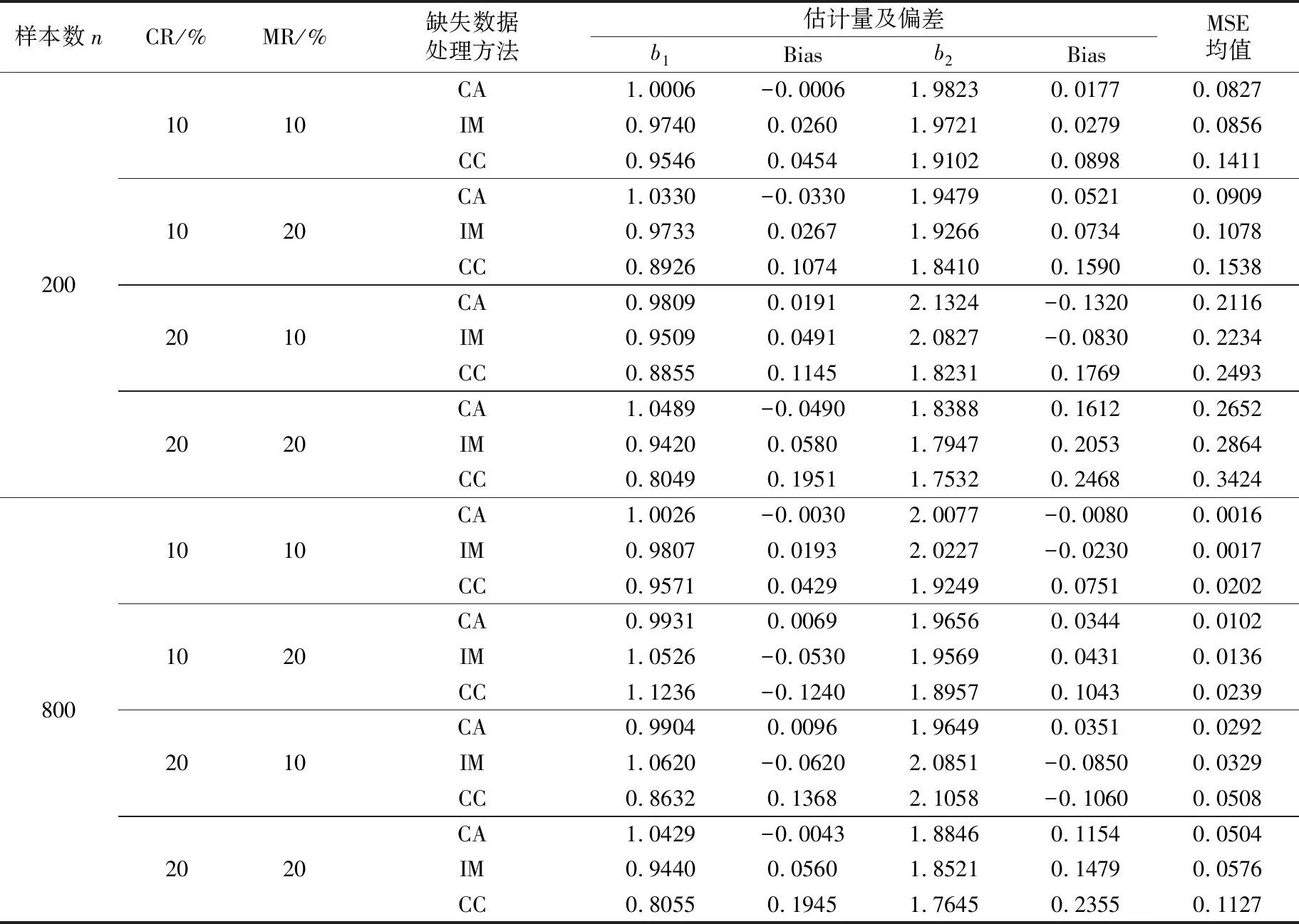
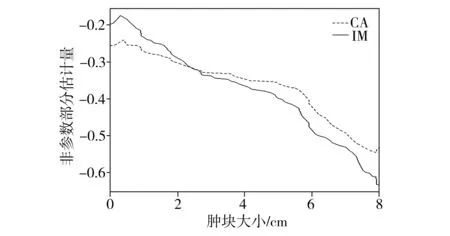
(C2) 協(xié)變量U有密度函數fU(u)且存在兩個常數c1和c2,使得在[a,b]區(qū)間上,有0 (C3)Ci獨立于(Zi,Ui)和Ti。 (C4) 對于任何t∈[0,τ],P(t≤T≤C)≥ζ0,其中ζ0是正常數。 (C5)ε1,ε2,…,εn有共同的連續(xù)可微的概率密度函數f(·),滿足0 (C7) 定義aH=inf{t∶H(t)=1},aG=inf{t∶G(t)=1},令aH 條件(C1~C2)是一般性假定,條件(C3~C5)是生存分析背景下的常規(guī)設定,條件(C6)保證定理1的證明中所定義矩陣D的特征值是有界的并且遠離零,條件(C7)表示G(Yi)遠離零。 關于估計量的性質,本文有下述結論。 定理1假設條件(C1~C7)成立,可以得到 其中,D1和Σ的定義在定理1的證明中給出。假設mn=O(n1/(2p+1)),定理1的結論(II)也可寫為 引理2假設條件(C1~C7)成立,最小化式(8)等同于最小化下式: (9) 同時,可以得到 因此A2=op(1),A3=op(1)。 基于以上結論,可以得到 (10) (11) 而 =op(1) (12) (13) 根據引理1和引理2,可以得到 (14) 結合式 (13) 和式(14) 就可以得到式(11)。 定義如下矩陣: D-1= 令 =op(1)。 下面證明定理1的結論(II)。由式(11)也可得到: 則可以得到 因此, (15) 根據I2的定義與如下等式: 有 (16) 結合式 (15)~式(16),有 因此 本文采用R軟件中的lpsolve包解決此線性規(guī)劃問題。 樣本數據由以下模型產生: Ti=b1zi1+b2zi2+α(Ui)Xi+εi,i=1,…,n (17) 評價非參數部分估計效果采用均方誤差指標: (18) 本文應用3種方法處理缺失數據:校準方法(Calibration Method, CA)和插補方法 (Imputation Method, IM)以及完全記錄分析(Complete Case Analysis, CC)方法。CC方法的基本思路就是直接忽略那些有缺失記錄的個體,再用傳統(tǒng)的統(tǒng)計分析方法去處理剩下的數據集,該方法的缺點是,當缺失數據太多時得不到有效的估計。IM方法是對缺失的數據進行填補,然后再用傳統(tǒng)的統(tǒng)計分析方法去處理整個數據集,其缺點也很明顯,對缺失的數據進行填補亦要選擇合適的方法,否則不會得到較好的估計。CA方法是用當前的可觀測數據來估計參數,通過給定參數的形式產生模擬數據,即對包含缺失在內的整個數據集進行估計。 設置模擬次數為200、q=5,誤差服從N(0,1)和t(5)分布的計算結果分別見表1和表2,其中MSE為200次模擬均值。另外,在表1中,CR為10%和20%時所對應的刪失時間指數分布參數分別為0.1和0.19;在表2中,CR為10%和20%所對應的刪失時間指數分布參數分別為0.08和0.16。 從表1和表2的結果可以看出:①對比不同的處理缺失數據方法,CA方法最好,IM方法其次,CC方法最差,表明本案例選用數據校準方法比較合適,而CC方法在不是完全隨機缺失的假設下只能得到有偏的估計,所以在本案例中的估計效果是最差的。②隨著樣本數量的增多,估計結果的偏差也逐漸變小,這與估計的大樣本性相符。③當刪失率和丟失率增大時,估計偏差隨之變大,這也從側面說明了估計的大樣本性,在足夠的樣本容量下,配合適當的估計方法才能得到好的估計結果。④在樣本量一定的情況下,相較于丟失率的變化,刪失率的變化對最后的估計結果影響更大。 實例分析數據來源于文獻[15]。該數據是基于“東部腫瘤合作組織”(Eastern Cooperative Oncology Group)進行的一次臨床試驗,其對象是II 期女性乳腺癌患者,目的是比較三苯氧胺(tamoxifen)和安慰劑對于該病的療效。在參與試驗的170 名對象中,只關注其中79 個在試驗結束前死亡的病患。根據報告可知,這個試驗的死亡原因數據并不完全。在這79 個死亡對象中, 44人死于乳腺癌,17 人死于已知的其他原因,剩下的18 名死于未知原因。為了適用于本文模型,在下面的數據分析中,采用的都是生存時間(單位:d)的對數值,記作Y。設指標δ顯示死亡是否由乳腺癌引起,指標ξ顯示死因是否已知。另外,變量Z1表示病人服用藥物情況(1,三苯氧胺;0,安慰劑);變量Z2表示病人雌激素受體蛋白狀態(tài)(1,陽性;0,陰性);X為病人腋淋巴結個數;U為腫塊的大小。模型如下: 表1 誤差服從N(0,1)分布的模擬結果 表2 誤差服從t(5)分布的模擬結果 Y=b1Z1+b2Z2+α(U)X+ε (19) 實例分析時采用的缺失數據處理方法為CA和IM,參數估計結果見表3,非參數部分的估計結果見圖1。由表3可見,所有的系數估計值都是正值,但是變量Z1的系數估計值比較小,也就是說,乳腺癌患者的生存時間雖然沒有受到“是否接受藥物治療”這個因素的顯著性影響,但若服用三苯氧胺,病人存活的時間還是可以延長;另外雌激素受體蛋白狀態(tài)為陽性也能增加生存時間,變量Z2的系數相對比較大,可見該因素對乳腺癌患者生存時間的影響更顯著一些。上述計算結果與文獻[11]的結論基本一致。根據圖1,非參數部分估計值意味著腫塊的增大會導致生存時間的減少,這與文獻[15]中的試驗結果是一致的。 表3 參數估計結果 圖1 非參數部分估計結果 [1] Cox D R. Regression models and life-tables[J]. Journal of the Royal Statistical Society: Series B, 1972,34(2):187-220. [2] Cox D R, Oakes D. Analysis of survival data[M]. London: Chapman and Hall, 1984:593. [3] Zhang W Y, Lee S-Y, Song X Y. Local polynomial fitting in semivarying coefficient model[J]. Journal of Multivariate Analysis, 2002,82:166-188. [4] Fan G L, Liang H Y, Shen Y. Penalized empirical likelihood for high-dimensional partially linear varying coefficient model with measurement errors[J]. Journal of Multivariate Analysis, 2016,147:183-201 [5] Zhao W H, Zhang R Q, Liu J C, et al. Robust and efficient variable selection for semiparametric partially linear varying coefficient model based on modal regression[J]. Annals of the Institute of Statistical Mathematics,2014,66(1):165-191. [6] 何曉霞,劉熙,王志明.右刪失數據下回歸函數的局部組合分位數回歸估計[J].武漢科技大學學報,2016,39(4):309-316. [7] Wang H J, Zhu Z Y, Zhou J H. Quantile regression in partially linear varying coefficient models[J]. The Annals of Statistics, 2009,37(6B):3841-3866. [8] Shen Y, Liang H Y. Quantile regression for partially linear varying-coefficient model with censoring indicators missing at random[J]. Computational Statistics and Data Analysis, 2018,117:1-18. [9] Huang J, Horowitz J L, Wei F R. Variable selection in nonparametric additive models[J]. The Annals of Statistics, 2010,38(4):2282-2313. [10] Schumaker L L. Spline functions: basic theory[M]. New Jersey: John Wiley & Sons, Inc.,1981. [11] 李夏炎.刪失指示量隨機缺失情況下回歸模型統(tǒng)計推斷[D].合肥:中國科學技術大學, 2011. [12] Wang Q H, Dinse G E. Linear regression analysis of survival data with missing censoring indicators[J]. Lifetime Data Analysis, 2011,17(2):256-279. [13] Hjort N L, Pollard D. Asymptotics for minimisers of convex processes[R/OL]. (2011-07-19)[2018-12-13]. https://arxiv.org/abs/1107.3806. [14] Knight K. Limiting distributions for L1regression estimators under general conditions[J]. The Annals of Statistics, 1998,26(2):755-770. [15] Cummings F J, Gray R, Davis T E, et al. Tamoxifen versus placebo: double-blind adjuvant trial in elderly women with stage II breast cancer[J]. NCI Monographs: a Publication of the National Cancer Institute, 1986 (1):119-123.
3 定理的證明
3.1 三條引理
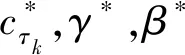
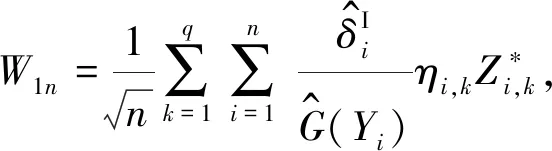
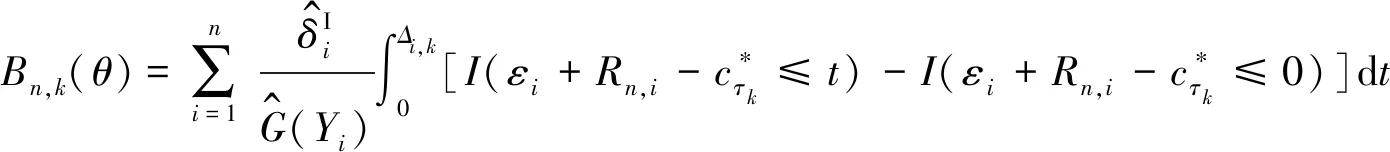

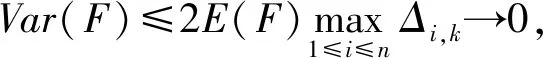
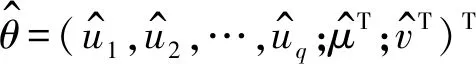
3.2 定理1的證明


4 數值模擬與實例驗證
4.1 蒙特卡洛模擬
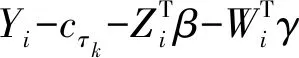

4.2 實例分析