基于蒙特卡洛采樣的橡膠復合材料內部導電網絡建模研究

劉蔓霄，陶青川，趙鳳媛

（四川大學電子信息學院，成都 610065）

0 引言

近年來隨著人工智能的發展，智能穿戴讓我們的生活越來越便利，這時好的傳感器材料就顯得尤為重要。由于導電橡膠在抗靜電、電磁屏蔽、過流/過熱保護、力敏和氣敏良好等優點，近年成為國內外研究重點。導電橡膠材料的導電性能最終是由其所形成的導電網絡所決定，因此，設計和構建有效的導電網絡是改善材料導電性能的根本途徑。由于近年來復合材料的更新，國內外少有人對橡膠材料的內部導電網絡進行研究。本文根據前人對碳納米管研究，圍繞橡膠材料的逾滲閾值、慘雜物濃度和長徑比對材料導電率影響為研究重點。研究過程基于三維空間，通過蒙特卡洛采樣模擬出在以均勻排列天然橡膠膠乳球為基底、隨機位置填充的碳納米管為導電體的可穿戴傳感器材料的內部導電網絡，如圖1（a）所示。由于膠乳球是不導電的，碳納米管的導電網絡構成了整個材料導電特性，如圖1（b）所示。通過大量實驗模擬材料內部網絡的結構，建立導電網絡結點方程，計算單位體積內材料的導電率模擬實體材料的導電率，從而分析材料的導電性能。

圖1

1 導電網絡的構建

不同于單根碳納米管，柔性傳感器材料的性質取決于分散于基體中的無數碳納米管相互之間的作用。聚合物基底一般不導電，導電的碳納米管隨機分散，如果濃度過低，那么材料內部沒有完整的導電通路。當碳納米管的濃度達到一個閾值時，材料內部形成相互連通的導電網絡，復合材料表現出導電性。與一般的碳納米管復合材料相比，帶橡膠球體的復合材料能夠節約大量的碳納米管材料，同時導電性能更好，形變的靈敏度也更好。

1. 1 滲流網絡模型及隧道效應模型

導電橡膠材料內部的碳納米管的分布與濃度決定了材料的導電性，研究整個導電網絡的導電性的前提是了解碳納米管的導電特性。碳納米管與普通炭黑、金屬顆粒不同，具有納米級直徑與較高的長徑比。納米級的導電填充物中微觀粒子存在雷布羅意理論[1]中的波粒二象性。電摻雜物之間不是像滲流理論[2]描述那樣，完全“接觸”時才能形成導電網絡。針對于納米級的顆粒，由于范德華力的作用，顆粒間的間隙h與顆粒尺寸相當時，顆粒之間的連接存在隧道效應的作用。Simmons[3]等人計算出顆粒間的隧道效應電導可以表示為：

?0是顆粒間間隙最小時的電導率，x是隧穿概率最小距離，在1nm級，h是顆粒間的距離。由上式可以看出當顆粒尺寸很大時，顆粒位置的稍微變化都會讓電導率發生很大變化，而且只有當顆粒緊密接觸網絡才是導通的。當顆粒直徑D接近于nm級時，在一定連通網絡的顆粒濃度下，增加顆粒的濃度并不會較大改變接入網絡的顆粒數，而是會影響顆粒間的間隙。Balberg[4]對納米級顆粒與的滲流模型做了具體分析，結果表示納米級的Ni導電粒子在不考慮隧穿效應時仿真曲線與實驗結果偏差太大，當考慮隧穿效應時仿真曲線與實驗結果比較相符。在王志峰[5]、唐力[6]等人的研究中可以看出碳納米管之間的導電特性也應該考慮隧道效應，而且當碳納米管電導率>10^4S/m時隧道效應引起的電阻還在網絡中可能占主導地位。

從前面的分析可以知道，碳納米管導電網絡的實際電阻由兩部分組成：①連接在通路中的碳納米管的本征電阻Rd；②由隧道效應引起的碳納米管之間的有效間隙的結電阻Rg。

本征電阻Rd可以表示為：

L表示接入到電路中的有效碳納米 管長度，δCNT表示碳納米管的本征電導率，D表示碳納米管直徑。對于結電阻，我們選取硬核模型的碳納米管為研究對象。當CNT之間的接觸距離大于0小于隧穿截止距離hcutoff時，此時兩管之間電子隧穿效應，有電流流過，可以導電，此時結電阻為Rg。根據Simmons[3]等人的研究結果，碳納米管結電阻可以如下表示：

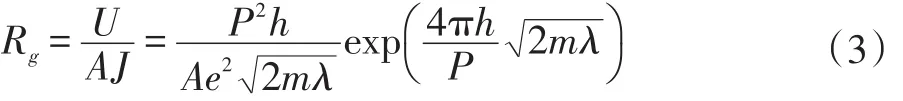
其中，U是結電勢差，A是隧道截面積可用碳納米管直徑D的平方代替，J是隧道電流密度，P是普朗克常數，h是兩根碳納米管的間距（中心軸線距離），e是電子電荷，m是電子質量，P是普朗克常數，λ是勢壘高度。

1. 2 碳納米管微觀網絡建模

如圖2（a）所示，我們選擇帶有半球形帽的實心圓柱來模擬硬核碳納米管，圓柱外面包裹一層厚度為的隧道效應有效作用區。碳納米管生成隨機坐標A(Ax,Ay,Az)作為一條CNT的起點，然后生成隨機單位向量，根據式（4）可以得到終點坐標B(Bx,By,Bz)。通過上訴CNT產生過程，基本的導電網絡結構模型就有了，如圖1（b）所示。接下來我們便要根據模型與預先設定的hcutoff，建立每根CNT之間的關系，從而計算網絡導電率。

圖2

以上的工作已經建立了內部CNT的相互關系，但是我們的目標是要計算單位體積網絡的電阻值。接下來我們就要計算完整的導電網絡，首先將未經篩選的整個網絡轉換成無向圖。基于圖像的連通域尋找算法的啟發，我們選擇了基于圖論的寬度優先遍歷（BFS）算法。相對于文獻[6]的迪杰斯特拉算法，選擇此算法的原因主要有以下兩點：①寬度優先遍歷基于隊列的實現模式，時間復雜度為O（n），可以節約大量的計算時間。算法示意圖如圖3。②我們后期用節點電壓法計算網絡電阻值時可以把那些在網絡中支路但電流為0的CNT納入計算，并不會影響最后計算結果。如圖3中紅色部分CNT，雖然在網絡中，但是支路電流為0。

圖3 BFS算法示意圖

2 網絡電路通路解算

上節已經介紹了獲取導電網絡的建模步驟，下面將具體針對復合材料內部導電網絡進行數值分析。對碳納米管導電網絡進行數值計算過程中，首先需要將碳納米管網絡等效成純電阻網絡，然后再對純電阻網絡求解其等效電阻和電導率。

2. 1 節點電壓分析法

節點電壓法實質是基于基爾霍夫電流定律。基爾霍夫電流定律是指對任意電路中的節點而言，所有流入該節點的電流的總和等于所有流出這個節點的電流的總和。假設進入某個節點的電流為正值，離開這個節點的電流為負值，則所有涉及這節點的電流的代數和等于零。通常我們選取一個節點為參考節點（作為0電勢點），其余n-1個節點到此節點的電壓為ui。

在RVE空間導電網絡中選取一小部分參與導電的碳納米管進行分析。經過轉化后形成的等效電阻如圖4所示，其中Rd表示接入網絡中碳納米管的本征電阻，Rg表示的是兩根碳納米管之間的結電阻，其電阻值得計算方法在上一節中已經具體討論。

2. 2 建立網絡節點方程

有了建立方程組的理論基礎，我們接下來討論怎么建立方程組。在我們研究模型中通常參與導電的CNT有上百根，按照節點電壓法節點數也會很多。首先我們需要找出所有的節點才能建立節點方程。我們需要根據結電阻與本征電阻建立起網絡的節點方程。如圖5所示，紅色圓圈表示需要建立的節點，通過節點來表示本征電阻與結電阻之間的串并聯關系。

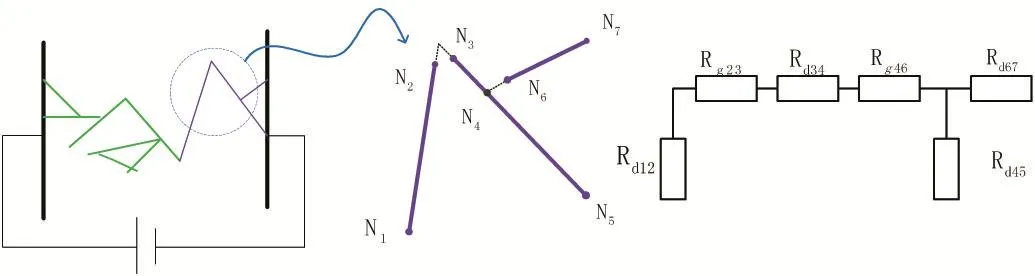
圖4 導電網絡向電阻計算的轉化過程

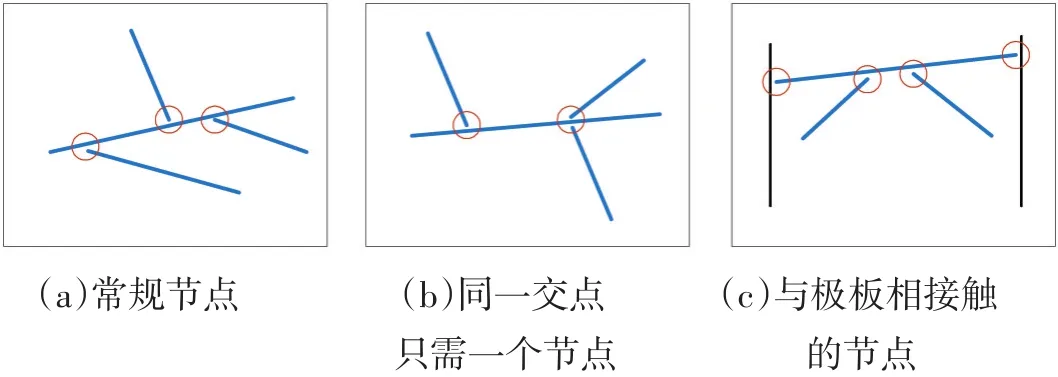
圖5

根據上面步驟可以標記所有的節點，根據基爾霍夫定律第一定律和歐姆定律，通過節點n的電流可以表示為：

我們假設網絡中與左極板相接觸的所有節點作為一個初始節點（n=1），電流I1為1A。與右極板相接觸的所有節點作為一個末節點（n=k），電流I1為-1A。導電網絡內部流過其余節點的總電流恒為0。設節點1的電勢為0，則節點n的電勢為un。根據節點電壓法和上式可以構造導電網絡內各節點的電流、電壓與電導的關系方程組如下式：

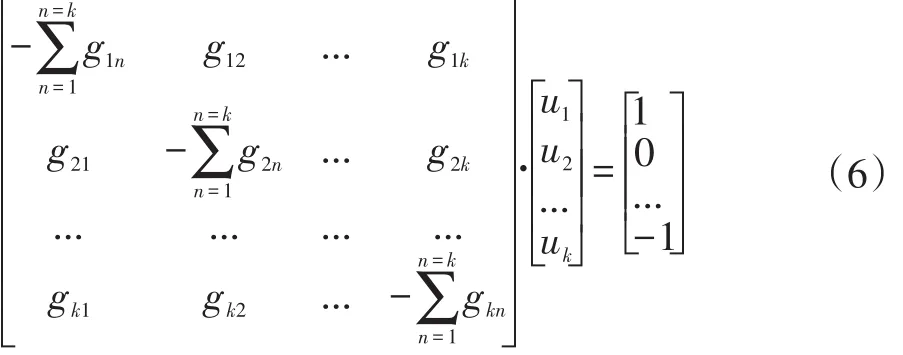
gkn為節點k和n之間的電導，表示與節點k相連的所有電導之和。由于復合材料中只有導電慘雜物的濃度達到一定時，才會有完整的網絡形成，所以一般k值會比較大，對計算方程的解造成困難。我們把沒有互相連接的節點看成電阻無窮大，故而電導記為0，這樣我們的方程組中將會有大量的0形成稀疏矩陣，方便了我們的計算。

根據歐姆定律，碳納米管導電網絡的等效電阻在數值上等于左極板和右極板之間的電勢差與流過他們的電流之比。假設輸入電流為1A，所以根據方程式（7）可以計算出等效電阻，那么導電網絡電阻率為：

其中L是基底材料沿著導電方向的長度，也就是兩極板之間的距離，S為垂直于導電方向的網絡空間的截面積，也就是基底的寬×高。

3 實驗結果與分析

建立了導電網絡模型，我們就要開始用模型去驗證開始的假設是否合理。首先導電網絡的導電性主要取決于網絡中碳納米管的本征電阻與隧道效應引起的段電阻。在王志峰[5]等人的研究中發現當導電率ρ>104S/m時，結電阻起主導作用。這時我們首先得確定網絡的hcutoff（為了方便后面用HC代替），然后研究結電阻與本征電阻對導電網絡的貢獻。其次碳納米管的長徑比、濃度都影響著網絡的導電率，之后也需要一一討論。

3. 1 Hc值的討論

由第二節的討論我們知道最大隧道效應作用間隙HC不僅與碳納米管的功函數e、聚合物介電常數等有關，還與碳納米管的直徑、長徑比、濃度等有很大的關系。同時HC又可以通過設置模型中不同的H來得到。

由圖6（a）可知在長1um、長徑比100的碳納米管在濃度為1.1%與0.9%的情況下，材料的的導電率隨著H的增大而減少然后趨于穩定。濃度1.1%情況下，基本上在H=4左右，材料的導電率保持不變。濃度0.9%情況下，基本上在H=4.5左右，材料的導電率保持不變。說明濃度越大，HC越小。本文和對比文獻中的研究結果趨勢相同，但由于本文有橡膠球為基底，所以CNT的濃度在更低時便表現出了好的導電率，相對于文獻中的材料需要的慘雜物更少，節約了成本。

3. 2 本征電阻與結電阻的分布規律

由于網絡中主要是有結電阻與本征電阻組成，要討論網絡的導電性需要討論結電阻與本征電阻對網絡的貢獻。當我們只考慮結電阻時，本征電阻的CNT段看成是通路電阻為0。只考慮本征電阻時，在小于HC時的間隙看成是通路，結電阻為0。為了方便計算，定義結電阻與本征電阻對網絡的貢獻分別為Φ（Rg）、Φ（Rd），計算方式如下：

由圖7可見，在大于一定的CNT電導率下，結電阻的貢獻遠遠大于本征電阻。說明選定慘雜物比例時，可以確定是否需要計算本征電阻。本文的模擬計算中選擇的CNT電導率為10^4S/m，所以可以忽略掉本征電阻的貢獻。

圖6

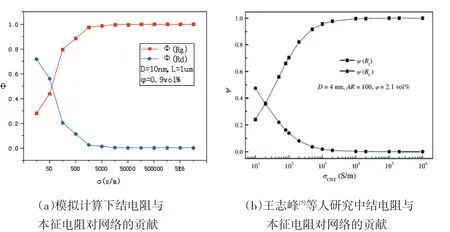
圖7

3. 3 長徑比與對微觀網絡影響

根據 Kirkpatrick[1]、Compton[2]的討論可知，復合材料的導電網絡兼有滲流效應與隧道效應的特點。網絡中的CNT長徑比、直徑、濃度等相關參數對網絡的導電性都有影響。模擬中設置基底為2.1um×2.1um×2.1um的立方體，含有8個直徑為1um的橡膠球，CNT濃度如表1的研究模型。研究了在CNT直徑為10nm情況下，不同濃度與不同長度下網絡的電導率。

由表1可以看出，在長徑不變的情況下隨著濃度的增加，電導率增加。在濃度不變的情況下隨著長徑比的增加，電導率增加。這和我們在上文中的討論與文獻[5-6]中的研究結果是一致的，同時結果也符合理論模型。

4 結語

本文基于前人在碳納米管復合材料網絡結構的研究基礎上，研究了以橡膠球為基底的碳納米管復合材料的內部網絡結構。在MATLAB 2015b平臺上建立仿真模型，研究了橡膠球為基底的碳納米管復合材料的內部網絡結構、隧道效應距離HC、CNT濃度和長徑比等對導電網絡的影響。結果表明，仿真模型符合理論原理與實際材料的導電特性。