基于用戶電器分類的智能電網實時定價研究

李軍祥，張文財，高 巖

(上海理工大學管理學院，上海 200093)

1 引言

隨著人類技術的進步，社會的發展需要消耗越來越多的電能，不但有已經普及的用電設備，像電視機、冰箱、洗衣機、空調等，還有逐漸普及的汽車充電、凈水器、空氣凈化器等家電也都在消耗著電能。假如在用電高峰期所有的電器都在運行的話，整個電網系統將是無法承受的。比如上海市用電整體水平已連續多年處于“緊平衡”狀態，在區外來電比例進一步增加,華東三條特高壓直流滿功率送電,高峰時段部分熱點地區供電仍較緊張。中商情報網報道,在2014年夏季，全網最高用電峰谷差達1300萬千瓦, 調峰壓力進一步加大，用電高峰期缺電200多萬千瓦，供需矛盾十分突出。雖然通過建立更多的發電廠和從區外調電是解決用電高峰的主要方法，但是花費大量資金用在電廠的建立和維護維修方面只是為了維持短暫的用電高峰，顯然并不明智,這種問題在中外的電力市場中都很突出[1]。

為了使發電量和用電量在用電高峰時期保持平衡，需求響應 (DR)的方法已經被運用到對居民的用電調控中，以達到削峰填谷的效果，田世明針對智能電網條件下的用戶需求響應展開深入分析，調研國內外需求響應的發展現狀，從需求響應概念、激勵機制、效益評估、支持平臺技術等方面對國內外學者在相關領域的研究成果進行總結[2]。DR動態定價包括分時定價 (TOU)、尖峰定價 (CPP)和實時定價 (RTP)[3]。分時定價指事先根據不同時間段制定不同的價格，在應用中一般分為峰谷平三個時段，上海現在使用的階梯定價就是分時定價，分時定價是一種靜態定價機制，只能反映電力系統的長期供電成本。尖峰定價指預先公布尖峰事件的設定標準以及對應的尖峰費率，并提前一定的時間通知用戶(通常為1天)，用戶可以做出相應的用電計劃調整。實時定價是不同時期實時發布不同價格。由于實時定價具有實時性，它可以使電力公司和用戶同時利益最大化，以達到需求響應所追求的用電量在峰期減少和轉移消耗，并及時改變用電模式的效果。一般地，用戶對不同的電價會有不同的反應。因此，實時定價是一種很理想的定價方式。

由于智能電表的產生，實時定價在未來的定價方式中將成為一種趨勢，智能電表除了具備傳統電表基本用電量的計量功能以外，它還具有用戶和電力公司、用戶和其他用戶進行數據交換的功能。一方面，可以使電力公司根據用戶的用電情況調整發電量和電價，另一方面，對于用戶可以根據電力公司發布的電價同時調整自己的用電方式，使整個電力系統達到最優的效果。智能電表的上述功能需要其具有對電器進行分類識別的能力。

目前比較流行的兩種電器識別方法有非侵入式和侵入式兩種方法。非侵入式的方法是把智能電表安放在用電用戶和電網的電能接口處來實時監控用電情況以及記錄相關信息，通過用戶的用電特征進行計算分析識別用電器。侵入式方法是在每個用電器上安裝計量電表，根據各個用電電器內置的電量計量設備，精確地顯示出某個時刻的用戶所用電器的用電量，像是手機管家可檢測到每個APP各個時刻內所使用流量。智能電表在今后的作用中不但可以實現數據的交換，而且還能對所用電器的用電量進行統計，因為不同的電器有不同的用電方式。目前一些學者就是通過分析所有電器的總用電過程進行分析，一些文章已經證實了用電負荷的識別準確度可達到90%[4-7]。M. Gonzalez等人是基于動態的電力消耗水平，根據用電開始時間、結束時間、時間周期、能量消耗等數據進行用電識別，這種方法識別電器的準確度超過90%[4]。李靜和楊洪耕介紹了一種對大功率電器進行識別的模糊算法[5]。同時，取家用電器正常工作時的穩態和暫態功率特性作為特征量，通過比較測量數據與數據庫模板的相似度來確定用電負荷的類別、工作狀態，然后匹配開關事件得到相應的耗電量[6]，B. Liao 和R. Ma運用神經網絡模型方法進行識別[7]，劉博等是根據用戶的種類進行實時定價[8]，Kazempour基于用電信息實時特征構建了一個多階段隨機互補模型來刻畫用戶用電行為以獲得用戶實時競價曲線，但卻沒有體現出智能電網環境下基于價格的需求響應機制[9]。代業明等研究了在電力零售商和用戶之間制定合同電量但不確定價格情況下進行實時雙邊合同談判過程，實時電價主要取決于雙方談判成本及各自對對方關于實時電力價格的預期估計，以此可以制定合理的實時電價，但這樣雖然達到合理的實時定價，但限于理論實際運用起來非常麻煩[10]。

本文是在對電器進行分類識別的基礎上研究的一種實時定價模型。在該模型中，首先把用戶分成不同類型，再對不同類型用戶的電器進行分類，電力公司根據不同類型用戶的用電設備類型的用電情況實時制定出不同的價格，用戶則根據不同類型電器的電價考慮是否在該時段使用該電器，最終使用戶和電力公司的效用最大，從而在用戶滿意的情況下使整個電力系統達到削峰填谷的效果。最后通過數值仿真驗證了電器分類模型更有效、更實用。

2 模型建立

由于家庭用戶和商業用戶的用電模式也不盡相同，比如家庭用戶一般有一個用電高峰，比如下班后在晚上的某個時段；商業用戶一般在上午和下午分別各有一個用電高峰時段，因此，在建立用電供需方系統模型前，首先根據現有環境將用戶分為商業用戶和家庭用戶。在電器分類方面，為研究方便，每類用戶的電器也都分為兩類。商業用戶所用電器分為商業基本用電電器(比如生產加工設備)和商業消耗用電電器(比如空駛的電梯)；家庭用戶的電器分為家庭基本用電電器和家庭享受用電電器。家庭基本用電電器指家庭為滿足基本生活所使用的電器，比如冰箱；家庭享受用電電器指用戶為了滿足自身的特殊需要而使用的電器，比如汽車充電，這類電器可隨時調整使用時間。

為了研究模型所達到的實際效果，常常需要用戶的效用函數值和福利值的概念。用戶的效用函數值是用戶在不同電價時的用電滿意度的測量值。在得出兩類用戶的用電效用值后，用效用值減去用電成本即為其所得福利值，即用戶的受益程度。整個用電供需系統的理想狀態就是系統福利值最大。

現假設只有一個電力公司提供用電，這比較符合當前的實際現狀。Wang Qingsi等[11]在研究智能電網動態定價時也是假設一個電力公司。當然也有像Bu Shengrong等[12]假設了多個電力公司相互競爭的情況下的實時定價，本文暫不研究多個電力公司的供電。每個用戶都裝有能進行電器識別的智能電表(ECC)與電力公司進行數據交換[13]。這類電表能收集所有不同用戶和不同電器種類的用電消費需求，也能收到電力公司實時制定的不同電器的用電價格，以便能引導用戶進行相應的電器消費調整。

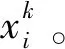
(1)

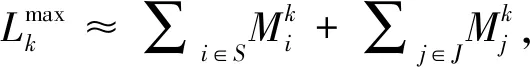
(2)

(3)

(4)

(5)

(6)

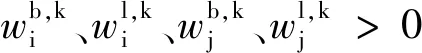
(7)

商業用戶i的總效用

(8)

家庭用戶j的總效用

(9)

對于商業用戶i，福利函數是其效用值減去其花費的最終結果：

(10)

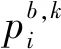
(11)

(12)

(13)

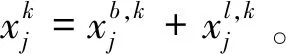
(14)

在此使用拉格朗日乘子法，它可以把對偶問題分成幾個可解的子問題，而且獲得的拉格朗日乘子恰恰是電力公司需要制定的最優價格[13]。設對偶問題的目標函數為Ψ，則

(15)

其中λs≥0，1≤s≤4是拉格朗日乘子。則問題(14)的對偶問題為

(16)

s.t.λ≥0

其中λ=[λ1,…,λ4]，

由(15)，可得：

其中：

(17)

(18)

(19)

(20)

和

(21)

(22)

(23)

(24)

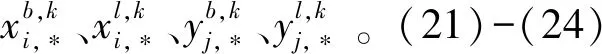
3 模型求解

(25)

即

(26)

(27)

(28)

(29)

γ1、γ2、γ3、γ4為步長，[θ]+表示θ與0相比較大的數。

4 實時定價算法過程

圖1是用戶和電力公司組成的電力系統流程圖，表示的是兩類用戶和電力公司的實時相互作用。兩者的算法過程在算法1(表1)和算法2(表1)中。

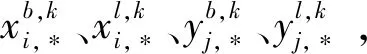
圖1 用戶和電力公司組成的電力系統流程圖

表1 用電用戶的算法過程

算法1:對于每個商業、家庭用戶i∈S、j∈J1:數據初始化2:開始循環3:從電力公司得到各類電器電價 λ1、λ2、λ3、λ44:解(17)-(20)得最佳用電量 xb,ki,?、xl,ki,?、yb,kj,?、yl,kj,?5:電力公司得到用戶的用電量6:結束循環

表2 電力公司的算法過程

算法2中，對于電力公司也以一個隨機值起始，從第2行到第9行是一個電力公司對用戶的反應過程。在這個循環中，第3行和第4行電力公司在每個時段k∈K中更新電價，并告知用戶。在第5行和第6行電力公司更新提供電量得到各個類型的最佳提供量，并在第7行更新用戶的總負荷。

5 數值試驗

在算法1中，我們假設有一個小規模的用電集體，其中有n=100個家庭用戶和m=50個商業用戶，應用這些用戶的行為來測試所提模型的有效性，并假設智能電表已經把所用電器分類好。根據文獻[12-14]，算法1和算法2的參數部分可以預先設置為α=20、β=25、ω=0.5、ψ=0.2、a=0.01、b=c=0、γ1=γ2=γ3=γ4=0.001。用戶在使用這4類電器時的用電意愿方面：w所表示的基本用電意愿的取值大小在范圍 [3,4]，w所表示的享受和消耗用電意愿的取值大小在范圍[1,2]，并在每個時段內求解最優的過程中保持不變，而電器未分類模型的用電意愿的取值大小在范圍[1,4]，時間上每天平均分成24個時段。在文獻[15]中電器未分類模型與固定定價模型進行對比效果明顯，本文是在文獻[12,16]實時電價模型的基礎上進行的電器分類，故在此電器分類模型只需與電器未分類模型進行比較，觀察分類模型是否有更好的效果。電器未分類模型中只需電價λ1=λ2=λ3=λ4，即無需區分電價。以下結果通過Matlab 12b軟件進行仿真求得。

首先我們先比較一下商業用戶按照前文方法進行電器分類后和分類前(即未分類)的一天用電量(耗電量)進行對比，如圖2所示。

圖2 商業用戶的電器分類和未分類模型用電量

由圖2我們可以看出：模型的耗電量線與其相對應供電量線基本重合，滿足在最高需求量和最低需求量之間，并且電器分類模型相比未分類模型表現出更好的削峰填谷效果。在用電總量大致相同的條件下，分類模型商業用戶的用電量在峰期階段峰值由未分類模型的102kw降到電器分類模型的85kw，在谷期階段電器分類模型的用電量相比電器未分類模型也顯著提高。而且商業用戶在用電上表現出兩個峰值期，圖形走勢符合商業用戶一天的耗電量圖。

接下來，我們再看一下家庭用戶的情況。圖3是家庭用戶電器分類和未分類模型的一天用電量分布圖。

圖3 家庭用戶的電器分類和未分類模型用電量

由圖3可以看出：兩類模型的用電量也都較好地滿足在最大需求量和最小需求量之間，并且表現出了較好的削峰填谷效果。在用電總量大致相同的條件下，分類模型在峰期階段峰值由未分類模型的113kw降到電器分類模型的101kw，在谷期階段電器分類模型的值也顯著提高。

下面我們再比較一下兩類用戶在分類電器和未分類電器一天用電使用的平均效用情況，如圖4和圖5。

圖4 家庭用戶的電器分類和未分類模型的平均效用值

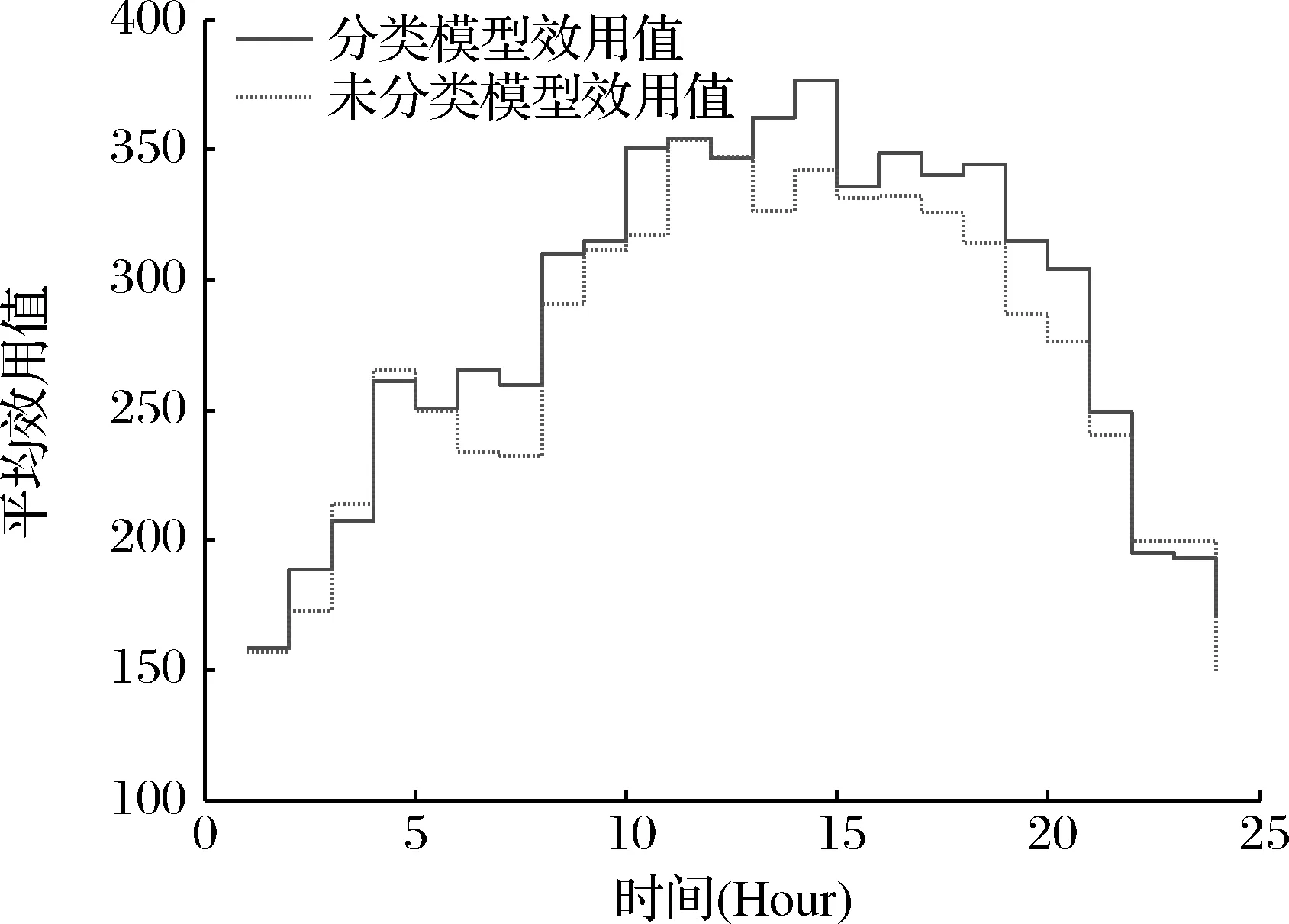
圖5 商業用戶的電器分類和未分類模型的平均效用值

從圖4和圖5中可以看出：整體上，電器分類模型的效用值高于電器未分類模型的效用值，但部分時段尤其是峰期也有電器未分類模型的效用值高于電器分類模型的效用值，這和模型峰期要消耗更多的電量追求效用值更大相一致。

最后，我們再比較一下用戶分類電器和未分類電器用電的整體福利效果，如圖6所示。

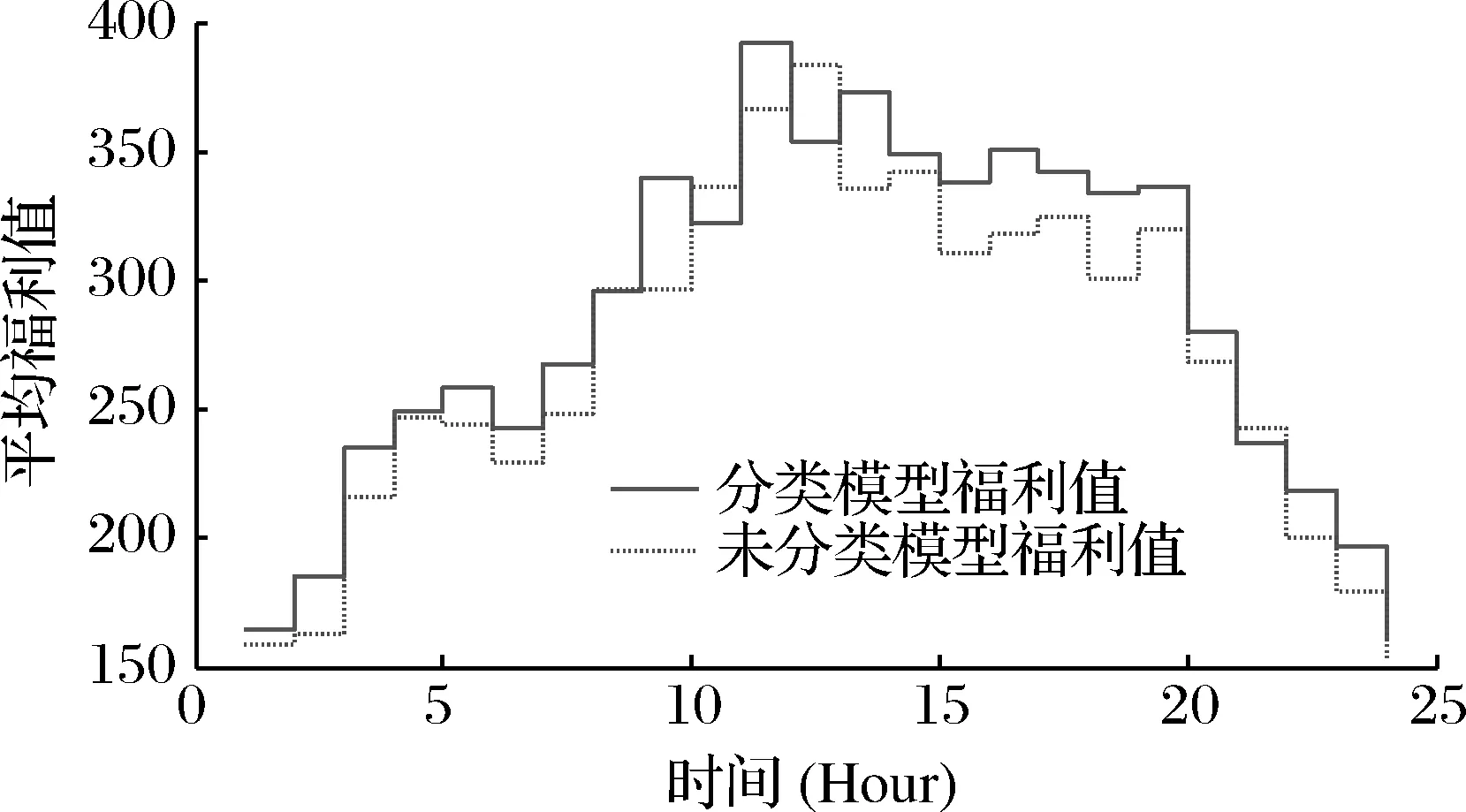
圖6 全部用戶的電器分類和未分類模型的平均福利值

從圖6中可以看出電器分類模型的平均福利值大致在各個時段內要高于電器未分類模型的平均福利值。從福利值的大小可以得出：用戶用這種實時電價分類模型要比未分類模型獲得更多的絕對收益。這就驗證了實時電價分類模型的有效性和實用性。

6 結語

隨著互聯網的發展和大數據、云計算在各領域中的廣泛應用，智能電表技術將來完全可以對居民所使用電器進行識別分類。本文針對智能電網提出了一種電器分類實時定價模型。針對不同類型的電器在不同的時段針對不同類型的用戶制定不同的價格，可以引導用戶在特定的時間內使用不同的電器，改變自己的用電模式，以使自身在整個電力供需系統達到用電成本最小的目的同時，能夠使用電效用值最大，獲得的福利值最高。最終并用數值實驗驗證了電器分類實時定價模型的有效性，且在峰值時段用電量明顯減少。在總用電量大致相同的情況下，效用值和福利值總體要比電器未分類實時定價模型要高。因此，電器分類定價或許是未來的一種定價方法，能有效的控制居民的用電行為。