一種基于CORDIC算法的改進型DDS設計

黃 瑋，崔喬冬，王堂勝，周彭宇，謝 帥，杜濱媛

（江蘇信息職業技術學院，江蘇 無錫 214000）

0 引 言

DDS即直接數字頻率合成技術，由美國學者J.Tiercy，M.Rader和B.Gold于1971年首次提出[1]。其結構主要包括相位累加器、只讀存儲器、數模轉換器和低通濾波器等。相對于第一代直接模擬頻率合成技術和第二代間接頻率合成技術來說，DDS技術具有頻率分辨率高、低功耗、速度快等優點。

DDS的設計方法有多種[2]。傳統的查找表法結構簡單，易實現，但精度較低，需要較大的ROM容量。多項式近似法對存儲容量的要求較低，精度較高，但電路結構復雜，工作速度較慢。CORDIC算法采用簡單的移位操作替代了原來復雜的計算，提升了計算速度，并能在存儲容量要求不高的情況下獲得較高精度。

DDS可以裝載并寄存用戶存入的頻率控制碼，根據控制碼進行相位累加，根據相位大小得到不同的電壓幅度，實現相位-幅度轉換。此時得到的一般是數字化的正弦波，還需要通過數模轉換器和低通濾波器得到可應用的模擬信號，即用戶所需的頻率。

1 DDS系統結構

一個典型的DDS系統結構（如圖1所示）通常包括四個部分[3]，分別為相位累加器（PA）、相幅轉換器（ROM）、數模轉換器（DAC）和低通濾波器（LPF）。其中，相幅轉換器是系統中最核心的部分，可以將相位轉換為幅度，對整個DDS的影響最大，是本次設計的重點。

實現相幅轉換器的方法有很多，包括查找表法、泰勒級數近似法等[4]，但其對存儲容量、計算精度等方面的需求無法滿足。CORDIC（Coordinate Rotation Digital Computer）算法采用坐標旋轉，可以計算三角函數、雙曲函數等基本功能函數。其通過加法運算、數據移位和迭代等基本操作實現函數計算。由于不需要乘法、除法等相對復雜的運算，因此不需要太多的存儲空間，且相應的電路結構不復雜，完全適用于DDS系統設計。

圖1 DDS結構原理

2 CORDIC算法的改進

CORDIC算法有兩種運算模式[5]，即旋轉模式和向量模式。本文中采用旋轉模式，設定基數，再通過一系列運算，實現角度的不斷調整，進而不斷逼近設定的旋轉角度。

傳統的CORDIC算法實現主要有循環迭代結構和流水線迭代結構兩種。循環迭代結構借助二選一的數據選擇器，不斷將計算結果輸入迭代結構，通過多次循環獲得所需值，所需存儲容量小，但每次只能進行一個運算，工作速度慢。而流水線結構可以使電路在時鐘周期內執行運算，運算量大，大大提升了工作效率。

為了達到簡化電路結構、節省存儲空間的目的，在傳統CORDIC算法的基礎上進行了改進，采用三角函數近似變換，使傳統CORDIC算法計算每次迭代的存儲角度時更為簡單。混合CORDIC算法結構圖如圖2所示。

圖2 混合CORDIC算法

CORDIC算法中總的輸入旋轉角度θ可以由一系列二進制數近似線性表示：

其中，?i∈{-1,1}，當?i為1時，角度沿逆時針方向旋轉；當?i為-1時，角度沿順時針方向旋轉，δ為角度近似誤差，滿足δ＜2-i，且2-i應盡可能小，以最大程度減小近似誤差。計算過程中，每次迭代存儲時的輸入角度為arctan2-k-1arctan2-k-1（其中k=0，1，2…）。當k足夠小時，arctan2-k-1≈2-k-1，如此一來，為了獲得所需要的精度，CORDIC算法中最后一次旋轉的角度需要小于2-i。

迭代計算過程中，不需要每次重新輸入。利用正余弦函數的對稱性，通過折疊象限，系統只需改變輸入角度區間內的初始相位，便能得到整個2π象限的正余弦函數值，從而可以確定區間的輸入。各區間所對應的輸入值如表1所示。

為了實現16位的系統精度，至少需要16位的字長，對于[0，π/4]內任意輸入的16位精度的任意角θ，可用二進制表示法表示：

其中，bi為符號位，bi∈{0,1}，進一步化簡為：

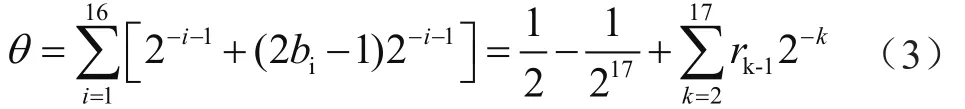
表1 各區間所對應的輸入值

其中，rk-1=2bi-1∈{-1,1}。由于精度要求16位，因此可將式（3）中的1/217項忽略，則為：

式（4）中，如果θ2所對應部分的迭代次數超過5時，可以用2-k代替arctan(2-k)，采用加法運算和移位等方式，從而輕松成多次迭代運算，節省了系統的存儲資源。此外，θ1可改寫為：

考慮到誤差需要進行變換，將θ1改寫為：

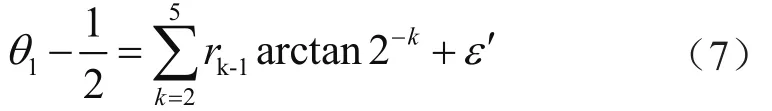
計算后發現，5次迭代后的誤差較小，不影響運算精度，如式（8）所示：

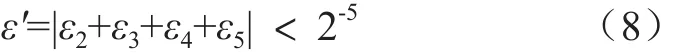
因此，可以直接轉換為二進制系數表示之前的旋轉方向，但ε'表示的近似誤差不能忽略。一般可將誤差合成，形成新的θ2'：

依據上述步驟進行反復推導，最終確定θ2部分的旋轉方向。但是，這種做法中的近似誤差需要進行額外計算，電路復雜度較高。若根據前次迭代的旋轉方向，預測每次迭代后的結果，雖然可以預測所有迭代的旋轉方向，但是存在誤差，仍需設置專門的電路模塊，比如進位保留加法器或超前進位加法器，增加了系統電路的復雜度。

為此，本文進行了以下改進，不再專門計算誤差，而是將前面迭代后的剩余角度都存入ROM，作為第5次迭代的角度輸入，與2-i（i≥6）進行比較，如此就無需計算近似誤差值ε'。改進后的結構示意圖如圖3所示。

改進算法根據輸入角度確定后續四次的迭代方向和相應的剩余角度，并由2-k直接代替arctan(2-k)確定剩余迭代的旋轉方向，從而完成所有迭代運算。

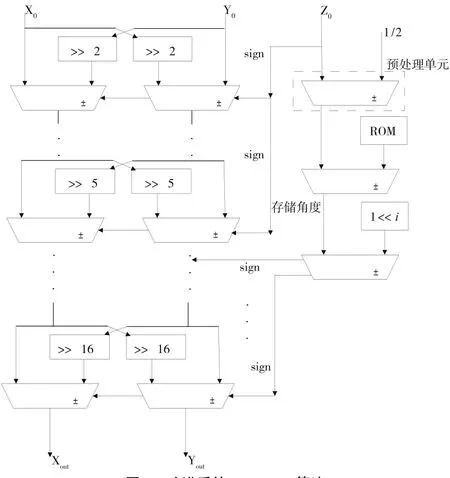
圖3 改進后的CORDIC算法

3 結 論

相幅轉換器是DDS結構的核心部分，本設計采用了CORDIC算法實現相幅轉換器，并且改進了傳統的CORDIC算法，減少了部分角度存儲，改善了傳統方法的局限性。