探究數學史中的勾股定理的證明

吳心培

【摘要】勾股定理又稱為畢達哥拉斯定理，在數學研究與應用中具有非常重要的地位和作用。目前，勾股定理已有許多種不同的證明方法，對中國古代和國外著名的勾股定理證明方法進行介紹，并對勾股定理的推廣應用進行闡述。

【關鍵詞】勾股定理 畢達哥拉斯定理 劉徽

一、引言

勾股定理也稱畢達哥拉斯（Pythagoras）定理，是數學中非常重要的定理之一。畢達哥拉斯是公元前6世紀希臘著名的數學家和哲學家，在西方，他被普遍認為是該定理最早的證明者，因此勾股定理就以他的名字命名。然而早在公元前1700年，古巴比倫人就發現已這一定理，無獨有偶，最遲公元前1105年，我國的商高便能利用一般的“弦圖”來證明這一定理。時至今日，勾股定理的證明方法已經有400多種了，其推論及應用仍具有重要影響。本文將對幾種著名的勾股定理的證明方法進行簡要介紹。

二、中國古代勾股定理的證明

1.《周髀算經》中商高的證明

《周髀算經》是我國古代最早的數學著作，其內容包括天文、數學知識，表現了我國古代人民的偉大智慧。《周髀算經》中記載了周公與大夫商高的一段話，商高當時回答說：“故折矩以為勾廣三，股修四，徑隅。既方其外，半之一矩，環而共盤。得成三、四、五，兩矩共長二十有五，是謂積矩。故禹之所以治天下者，此數之所由生也”。

英國人Joseph Needham將這段文字解釋為：把一個矩形沿對角線剪開（如下圖1所示），寬等于3個單位，長為4個單位。這樣兩對角之間的對角線長為5個單位。我們再用這條對角線為邊畫一個大正方形，再用幾個同上文的半矩形把這個大正方形圍起來，從而形成一個方形盤。像這樣，外面四個半矩形便構成了兩個矩形，這兩個矩形總面積是24，然后我們再從方形盤的總面積49中減去24，得到25。我們便稱這種方法為“積矩”。

雖然書中只以3，4，5為例，但這種方法也具有一般性，所以我們普遍認為商高已經證明了勾股定理。

2.《九章算術》中劉徽的證明

《九章算術》是《周髀算經》之后最重要的數學典籍，這部學術著作是由先秦到西漢中期眾多的學者修改編纂而成的，其在代數、幾何方面均有巨大成就。可以說，它代表著中國古代的機械算法體系，它與古希臘的《幾何原理》相得益彰，對東方的數學發展產生重要影響。

魏晉時期，著名數學家劉徽在為《九章算術》做批注時便給出了自己的證明：“勾自乘為朱方，股自乘為青方，令出入相補，各從其類，因就其余不動也。合成弦方之冪”，短短幾句便對勾股定理進行了清晰的描述。但十分可惜的是，劉徽的證明的圖已經失傳了。根據學者李迪的研究，劉徽的證明方法與歐幾里得在《幾何原本》中的證明描述相似，而根據學者曲安京先生的研究，劉徽的勾股定理證明方法如圖2所示，其他學者對劉徽的證明方法也有自己不同的理解和闡述。

3.《勾股舉隅》中梅文鼎的證明

梅文鼎是我國清代著名的學者，是民間數學家和天文學家，被譽為“國朝算學第一人”。對于勾股定理的證明，梅文鼎給出了兩種證明方法，其中一種方法與趙爽和劉徽的方法有異曲同工之妙。本文介紹梅文鼎另外一種獨具創造性的證明方法，具體步驟如下：

（1）以直角三角形ABC斜邊BC為邊作一個正方形BCDE，其面積為BC的平方，再過點A做BC的垂線KL，把正方形分割成面積為AC平方的四邊形DKLC與面積為AB平方的四邊形KEBL，如圖3所示。

（2）將三角形ALC，ALB移到FKD，FKE處，并做AI垂直于FD，做EN垂直于FE，如圖4所示。

（3）將三角形FLA，FEN移到DHC，EJM處，如圖5所示。

（4）將梯形ENAJ移到JMBG處，即可完成證明，如圖6所示。

三、國外勾股定理的證明

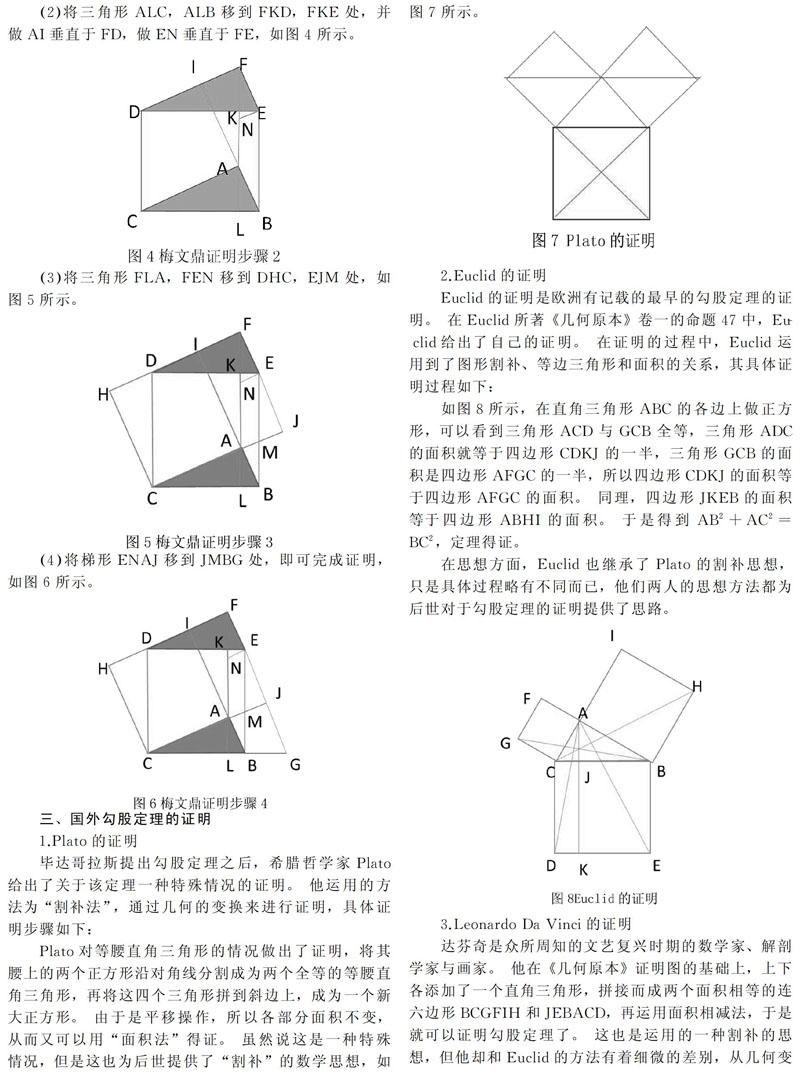
1.Plato的證明

畢達哥拉斯提出勾股定理之后，希臘哲學家Plato給出了關于該定理一種特殊情況的證明。他運用的方法為“割補法”，通過幾何的變換來進行證明，具體證明步驟如下：

Plato對等腰直角三角形的情況做出了證明，將其腰上的兩個正方形沿對角線分割成為兩個全等的等腰直角三角形，再將這四個三角形拼到斜邊上，成為一個新大正方形。由于是平移操作，所以各部分面積不變，從而又可以用“面積法”得證。雖然說這是一種特殊情況，但是這也為后世提供了“割補”的數學思想，如圖7所示。

2.Euclid的證明

Euclid的證明是歐洲有記載的最早的勾股定理的證明。在Euclid所著《幾何原本》卷一的命題47中，Euclid給出了自己的證明。在證明的過程中，Euclid運用到了圖形割補、等邊三角形和面積的關系，其具體證明過程如下：

如圖8所示，在直角三角形ABC的各邊上做正方形，可以看到三角形ACD與GCB全等，三角形ADC的面積就等于四邊形CDKJ的一半，三角形GCB的面積是四邊形AFGC的一半，所以四邊形CDKJ的面積等于四邊形AFGC的面積。同理，四邊形JKEB的面積等于四邊形ABHI的面積。于是得到AB2+AC2=BC2，定理得證。

在思想方面，Euclid也繼承了Plato的割補思想，只是具體過程略有不同而已，他們兩人的思想方法都為后世對于勾股定理的證明提供了思路。

3.Leonardo Da Vinci的證明

達芬奇是眾所周知的文藝復興時期的數學家、解剖學家與畫家。他在《幾何原本》證明圖的基礎上，上下各添加了一個直角三角形，拼接而成兩個面積相等的連六邊形BCGFIH和JEBACD，再運用面積相減法，于是就可以證明勾股定理了。這也是運用的一種割補的思想，但他卻和Euclid的方法有著細微的差別，從幾何變化的角度上來看的話，達芬奇主要運用的是旋轉和對稱，而后者運用的則是平移，如圖9所示。