基于貝葉斯公式的地下水污染源識別

張雙圣,強 靜,劉漢湖,劉喜坤,朱雪強

?

基于貝葉斯公式的地下水污染源識別

張雙圣1,3,強 靜2*,劉漢湖1,劉喜坤3,朱雪強1

(1.中國礦業大學環境與測繪學院,江蘇 徐州 221116；2.中國礦業大學數學學院,江蘇 徐州 221116；3.徐州市城區水資源管理處,江蘇 徐州 221018)

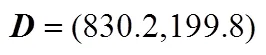
監測井優化；污染源識別；貝葉斯公式；信息熵；延遲拒絕自適應Metropolis算法；拉丁超立方抽樣；多目標優化模型

由于地下水污染的發現具有滯后性,事件發生的時間、地點和污染源的強度等污染源信息往往是未知的,因此能否準確地得到污染源的相關信息,對于地下水污染的治理具有重要的現實意義.

建立地下水水質運移模型,利用監測井處的污染物濃度監測值反求污染源位置、污染源釋放強度及釋放時間等信息,即為地下水污染源識別反問題,其本質是運用監測值對溶質運移模型參數進行反演與識別.目前,求解此反問題的方法主要包括貝葉斯統計方法[1]、地質統計學方法[2]微分進化算法[3]、遺傳算法[4]和模擬退火算法[5]等.這些算法可分為確定性方法和不確定性方法,其中確定性方法未考慮誤差因素,得到參數的一個確定的估計值,但容易丟掉“真值”;不確定性方法具有較強的隨機性,得到的是參數估計值的一個范圍,但保證了反演結果的可靠性.其中,貝葉斯統計方法以從監測值中獲取參數信息為目標,將參數先驗概率密度函數與樣本似然函數結合在一起,形成一套非常靈活、直觀、易于理解的統計方法,應用越來越廣泛.

在對模型參數進行反演識別時,貝葉斯統計方法中經常需要求解參數的后驗估計值或者后驗分布,在參數維數不是特別高時可以采用數值積分或者正態近似的方法求解[6].但是,隨著參數維數的增加,數值積分算法的計算量將呈指數增長,求解過程復雜而且難度較大,往往需要借助獨立抽樣的蒙特卡羅方法(MC方法)[7]進行近似求解,其中馬爾科夫鏈蒙特卡羅方法(MCMC方法)[8-13]作為一種經典抽樣方法得到廣泛應用.近些年,比較流行的MCMC算法主要包括經典Metropolis算法[8-9]、延遲拒絕算法(DR)[10],自適應Metropolis算法(AM)[11-12],延遲拒絕自適應Metropolis算法(DRAM)[13]等,但是這些算法均存在反演結果不收斂,或者局部最優的問題.

另一方面,受限于監測經費及客觀條件,監測方案[14-15](包括監測井的位置、數量及監測頻率)往往難以達到理想要求,造成監測數據包含的信息量不充分或者監測值和未知參數的關聯性較弱,且含有誤差,因此在對模型參數進行反演識別時,常常導致反問題不適定性[16].為達到理想的模型參數反演效果,需對監測井方案進行優化設計.首先需要定義目標函數,對監測井方案的信息量進行量化[15].監測方案優化中常用的目標函數有基于信息矩陣的A-最優,D-最優和E-最優等準則[15],信噪比(SNR)[17],基于貝葉斯公式的相對熵[14,15,18]等.其中基于信息矩陣的A-最優、D-最優和E-最優等準則適用于線性模型及參數分布假設為正態分布情形;信噪比、相對熵這2個指標適用于非線性模型及參數分布假設為非高斯情形[14,18].在現實案例中,地下水模型多為非線性模型,但是信噪比僅考慮監測誤差對監測數據的干擾影響,相對熵未考慮參數先驗分布對后驗分布的影響. 為此引入信息熵概念[19],信息熵是信息不確定性的度量,不確定性越大,信息熵越大.

1 研究方法

1.1 貝葉斯公式

貝葉斯公式[21]如下:

在實測數據固定的條件下,(6)式是關于參數的函數.通過積分求解參數的后驗分布很難得出顯式表達式,本研究采用MCMC方法對(6)式進行求解.

1.2 基于貝葉斯公式與信息熵的監測井優化設計

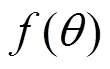
(12)

式(12) 的求解算法較為復雜,難以得出顯示表達式,本文運用蒙特卡羅方法[14]近似求解.

首先利用式(8)對式(12)改寫如下:

運用蒙特卡羅方法求解(14)式:

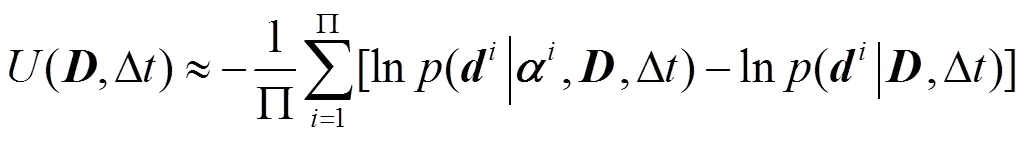
1.3 基于拉丁超立方抽樣的改進型多鏈延遲拒絕自適應Metropolis算法

Metropolis算法是一種經典的MCMC 方法,應用較為廣泛,但在在運用貝葉斯公式對模型參數進行反演識別時,Metropolis算法容易出現局部最優,或者難以收斂,而且抽樣效率低下的問題,本研究提出一種基于拉丁超立方抽樣的改進型多鏈延遲拒絕自適應Metropolis算法.

1.3.1 DRAM算法 延遲拒絕自適應Metropolis算法(DRAM)由Haario等[13]在2006年首次提出,是一種高效自適應MCMC方法,其本質是把DR算法和AM算法2者組合起來,既保證了馬爾科夫鏈的局部自適應,又保證了鏈條的全局自適應調整策略,因此DRAM算法的抽樣效率優于DR算法和AM算法各自單獨使用的情況[13].DRAM算法具體步驟如下:

(1)非自適應階段

③重復過程②,直至達到迭代次數0.

(2)自適應階段

③重復過程②,直至達到迭代次數.

1.3.2 基于拉丁超立方抽樣的改進型多鏈DRAM算法 為防止反演結果局部最優,或者產生難以收斂的問題,且保證樣本初始點的隨機性和均勻性,本研究采用基于拉丁超立方抽樣[22]方法優化抽樣過程.拉丁超立方抽樣是一種多維分層隨機抽樣方法,具有良好的散布均勻性和代表性.假設要在維模型參數先驗范圍[A,B](=1,2,…,)內抽取組樣本,具體步驟如下:

(1)把維模型參數的個先驗范圍[A,B] (=1,2,…,)都均分成個小區間,小區間可記為[A,B](=1,2,…,,=1,2,…,),總共產生′個小區間;

(4) 矩陣中每個列向量是1組樣本,共抽取得到組樣本.

基于拉丁超立方抽樣的改進型多鏈DRAM算法具體步驟:

第1步:運用拉丁超立方抽樣方法,在模型參數先驗范圍內隨機抽取組初始樣本.

第2步:分別以組初始樣本作為初始點采用DRAM算法進行迭代運算,得到條Markov Chains.

第3步:對上面條Markov Chains求平均值作為最終的結果.

此方法改進之處在于盡量削弱樣本初始點對算法結果的影響,符合Monte Carlo模擬方法的思想.

1.3.3改進型多鏈DRAM算法的收斂性判斷 本文采用Gelman-Rubin收斂診斷方法[23]對多鏈DRAM算法后50%采樣過程的收斂性進行判斷.收斂性判斷指標為:

2 算例應用

2.1 算例概述

假設研究區域內含水層為二維均質各向同性含水層,建立坐標系,在S范圍內向無限平面的均勻穩定流中注入某污染物,瞬時注入的質量為,為水流方向(圖1),則此時的對流-彌散方程[24]為:

式中:C為監測點在t時刻的污染物濃度, ;t為污染物排放后經過的時間,d;Dx、Dy分別為縱向、橫向的彌散系數,;u為含水層水流平均流速,.

方程的解析解可表示為:

式中:為污染物的排放強度,g;為含水層的厚度,m;、分別為距污染源的縱向、橫向距離,m;為含水層的有效孔隙率.

監測井位置為.區域水文地質參數如表1所示.

表1 研究區域水文地質參數

2.2 監測方案優化

表2 研究區域待求參數取值范圍

由1.2節可知,監測井位置優化問題可概化如下:

圖2 遺傳算法中每一代目標函數的最小值和平均值

式中:表示第組真實參數,表示參數的第個分量.

表3 11種監測方案,和

表4 從參數的先驗分布中得到20組真實參數

2.2.2 監測方案多目標優化模型 在現實生活中,污染源反演問題常常不僅需要優化監測方案以使反演誤差最小(即信息熵最小),同時為了盡快找到污染源還要求監測方案耗時最少,需要在信息熵和監測方案耗時之間進行權衡.設定監測次數仍為5次,以信息熵最小和監測耗時最短建立多目標優化模型,數學公式如下:

信息熵最小化目標:

監測耗時最短目標:

一般來說,多目標優化問題的最優解并不唯一,它的最優解集由那些任一個目標函數值的減少都必須以增加其他目標函數值為代價的解組成的集合,稱之為Pareto域.本文采用帶精英策略的非支配排序遺傳算法(NSGA-Ⅱ)解此多目標優化問題.NSGA-Ⅱ算法是由Deb等[20]在NSGA的基礎上提出的.

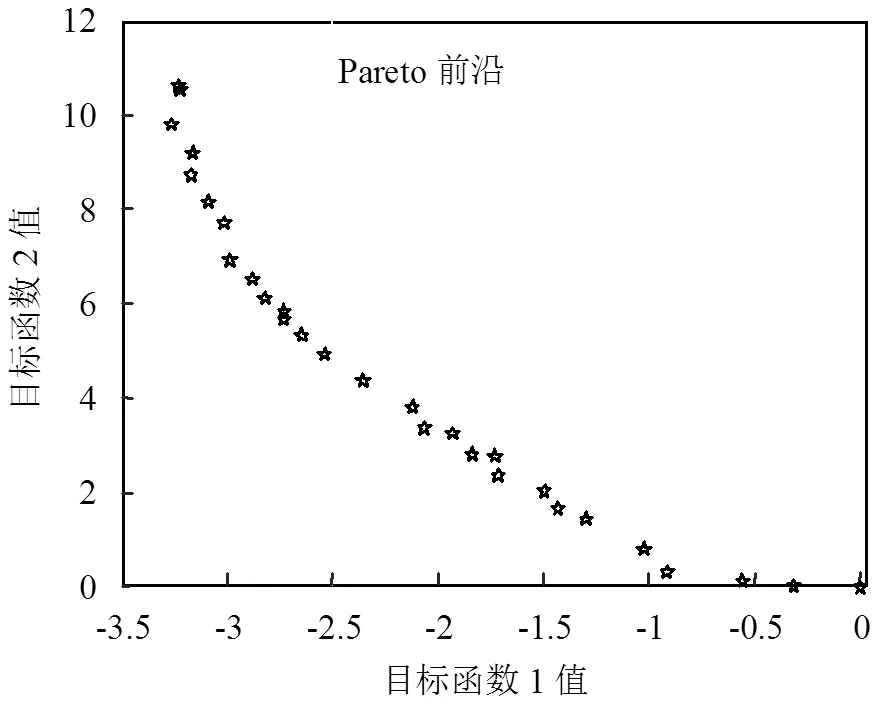
圖4 目標函數的Pareto前沿

NSGA-Ⅱ算法中參數如下設定:種群大小為100,最大進化代數為50,交叉系數為0.8,變異系數為0.2.運用Matlab中gamultiobj函數求解此多目標優化問題,得到目標函數的Pareto前沿,見圖4.

2.3 基于優化監測方案的污染源識別

由表5可知,2種監測方案下,4個參數反演中0,02個參數反演效果均較好,均值相對誤差都在4.0%內;而參數,0反演均值相對誤差在10%~ 20%,主要原因在于和0先驗分布范圍較0,0大,導致和0的后驗分布信息熵較大,其不確定性相應增大,進而反演誤差增大,因此為降低參數的反演誤差,需根據調查盡量縮小參數的先驗分布范圍.

另一方面,與基于單目標優化的監測方案反演結果相比,基于多目標優化的監測方案條件下,污染源參數的反演均值相對誤差雖分別增加了0.4%、0.2%、0.3%、2.9%,但監測時間卻顯著縮短了55.6%,因此基于多目標優化的監測方案對于污染源的快速識別更具有現實意義.

3 結論

3.1 信息熵是參數反演結果精度的有效量度,信息熵越小,參數反演結果精度越高.參數反演結果的誤差與其先驗分布范圍的選取有直接關系,參數先驗分布范圍越大,其后驗分布的信息熵較大,導致反演誤差增大.為降低參數的反演誤差,需根據調查盡量縮小參數的先驗分布范圍.

3.2 與單目標優化監測方案相比,多目標優化監測方案雖然增加了反演結果的誤差,但是卻能顯著縮短監測時間,對于污染源的快速識別更具有現實意義.

3.3 基于拉丁超立方抽樣的DRAM算法在保證反演結果準確性的前提下,可顯著提高反演效率,其可靠性和穩定性均優于經典Metropolis算法.

3.4 本文設計的案例為污染物在含水層中遷移的理想模型,具有解析解,在進行監測井的優化設計及污染源識別時,可將解析解公式通過matlab編程的方式嵌入到相關算法中,實現解析公式的反復調用.但在現實生活中,地下含水層的結構及排污過程較為復雜,地下水在含水介質中的遷移運動是一個十分復雜的系統,一般通過建立數學模型(沒有解析解),運用商業軟件(如GMS、Visual MODFLOW等)進行數值模擬求解.在運用貝葉斯公式和信息熵進行監測井優化設計及污染源識別時,需多次調用數值模擬模型,計算量巨大.本文采用地下水污染理想模型,既驗證了基于貝葉斯公式與信息熵的監測井優化設計方法的可行性,又強有力的減少了計算工作量.

[1] Chen M, Izady A, Abdalla O A, et al. A surrogate-based sensitivity quanti?cation and Bayesian inversion of a regional groundwater ?ow model [J]. Journal of Hydrology, 2018,557:826-837.

[2] Snodgrass M F, Kitanidis P K. A geostatistical approach to contaminant source identification [J]. Water Resources Research, 1997, 33(4):537-546.

[3] Ruzek B, Kvasnicka M. Differential evolution algorithm in the earthquake hypocenter location [J]. Pure and Applied Geophysics, 2001,158:667-693.

[4] Mahinthakumar G, Sayeed M. Hybrid genetic algorithm-local search methods for solving groundwater source identification inverse problems [J]. Journal of Water Resources Planning and Management, 2005,131(1):45-57.

[5] Dougherty D E, Marryott R A. Optimal groundwater management: 1. Simulated annealing [J]. Water Resources Research, 1991,27(10): 2493-2508.

[6] Tanner M A. Tools for statistical inference: methods for the expectation of posterior distribution and likelihood functions [M]. New York: Springer-Verlag, 1996:1-52.

[7] 李久輝,盧文喜,常振波,等.基于不確定性分析的地下水污染超標風險預警 [J]. 中國環境科學, 2017,37(6):2270-2277. Li J, Lu W, Chang Z, et al. Risk prediction of groundwater pollution based on uncertainty analysis [J]. China Environmental Science, 2017, 37(6):2270-2277.

[8] Metropolis N, Rosenbluth A W, Rosenbluth M N, et al. Equation of state calculations by fast computing machines [J]. The Journal of Chemical Physics, 1953,21(6):1087-1092.

[9] Hastings W K. Monte Carlo sampling methods using Markov chains and their applications [J]. Biometrika, 1970,57(1):97-109.

[10] Mira A. Ordering and improving the performance of Monte Carlo Markov Chains[J]. Statistical Science, 2002,16:340-350.

[11] Haario H, Saksman E, Tamminen J. An adaptive Metropolis algorithm[J]. Bernoulli, 2001,7(2):223-242.

[12] Xu W, Jiang C, Yan L, et al. An adaptive metropolis-hastings optimization algorithm of Bayesian estimation in non-stationary flood frequency analysis [J]. Water Resources Management, 2018,32(4): 1343-1366.

[13] Haario H, Laine M, Mira A. DRAM: Efficient adaptive MCMC [J]. Statistics and Computing, 2006,16(4):339-354.

[14] Huan X, Marzouk Y M. Simulation-based optimal Bayesian experimental design for nonlinear systems [J]. Journal of Computational Physics, 2013,232(1):288-317.

[15] 張江江.地下水污染源解析的貝葉斯監測設計與參數反演方法 [D]. 杭州:浙江大學, 2017. Zhang J. Bayesian monitoring design and parameter inversion for groundwater contaminant source identification [D]. Hangzhou: Zhejiang University, 2017.

[16] Carrera J, Neuman S P. Estimation of aquifer parameters under transient and steady state conditions: 2. Uniqueness, stability, and solution algorithms [J]. Water Resources Research, 1986,22(2):211- 227.

[17] Czanner G, Sarma S V, Eden U T, et al. A signal-to-noise ratio estimator for generalized linear model systems [J]. Lecture Notes in Engineering & Computer Science, 2008,2171(1).

[18] Lindley D V. On a measure of the information provided by an experiment [J]. The Annals of Mathematical Statistics, 1956,27(4): 986-1005.

[19] Shannon C E. A mathematical theory of communication [J]. The Bell System Technical Journal, 1948,27(3):379-423.

[20] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002,6(2):182-197.

[21] Berger J O. Recent development and applications of Bayesian analysis [D]. Proceedings 50th ISI, Book I. 1995.

[22] 戴英彪.基于拉丁超立方試驗設計的事故再現結果不確定性分析[D]. 長沙:長沙理工大學, 2011. Dai Y. Uncertainty analysis of vehicle accident reconstruction results based on Latin hypercube sampling [D]. Changsha: Changsha University of Science and Technology, 2011.

[23] Gelman A G, Rubin D B. Inference from iterative simulation using multiple sequences [J]. Statistical Science, 1992,7:457-472.

[24] 陳崇希,李國敏.地下水溶質運移理論及模型 [M]. 武漢:中國地質大學出版社, 1996:46-49. Chen C, Li G. Theory and model of solute transport in groundwater [M]. Wuhan: China University of Geosciences Press, 1996:46-49.

[25] 周圣武,李金玉,周長新.概率論與數理統計(第二版) [M]. 北京:煤炭工業出版社, 2007:208-215. Zhou S, Li J, Zhou C. Probability theory and mathematical statistics (Second edition) [M]. Beijin: China Coal Industry Publishing House, 2007:208-215.

Identification of groundwater pollution sources based on Bayes’ theorem.

ZHANG Shuang-sheng1,3, QIANG Jing2*, LIU Han-hu1, LIU Xi-kun3, ZHU Xue-qiang1

(1.School of Environment Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China；2.School of Mathematics, China University of Mining and Technology, Xuzhou 221116, China；3.Xuzhou City Water Resource Administrative Office, Xuzhou 221018, China)., 2019,39(4)：1568~1578

monitoring well optimization；contamination source identification；Bayes’ Theorem; information entropy；delayed rejection adaptive Metropolis algorithm；Latin hypercube sampling；multi-objective optimization model

X523

A

1000-6923(2019)04-1568-11

2018-08-20

國家自然科學基金資助項目(51774270);國家水體污染控制與治理科技重大專項基金資助項目(2015ZX07406005)

*責任作者, 講師, 57591340@qq.com

張雙圣(1983-),男,山東省昌邑市人,中國礦業大學博士研究生,主要從事地下水污染控制研究.發表論文20余篇