機器學習算法信用風險預測模型

(廣東電網有限責任公司， 廣州 510160)

0 引言

由于近年來國內金融行業的迅猛發展，伴隨著我國經濟的急速飛騰，銀行業務蓬勃發展。信貸業務是銀行的主流業務之一，但是如何評價借款人的信用風險已經成為當今互聯網金融行業的熱門課題之一，日益受到當代人的注意。

銀行客戶信用風險評估問題其本質為一個分類為題，也就是將現有的銀行用戶劃分為信譽用戶與非信譽用戶的過程。從其發展歷程來看，大致可以分為3個階段，樸素分析階段、概率分析階段、人工智能階段[1]。樸素分析階段主要為概率學應用于經濟領域之前的所有銀行借貸階段；

概率階段是指概率學運用到銀行金融領域開始直到人工智能在金融領域應用而結束[2]，此階段在我國主要是指上個世紀五十年代本世紀初。

第三階段也就是現階段，主要是指人工智能在信用評估中的應用，此階段從本世紀初開始直到現在[3]。

從國際角度講，消費者的信用評分美國的理論以及實際最為具有參考價值，其中例如Equifax公司[4]，該公司每天可以提供數百萬份的消費者信用分析報告。

同時從信貸領域將，美國信貸業務發展較為成熟，以上個世紀七十年代為例，美國信用卡發展達到了極致，甚至有的銀行為了搶占市場，直接將信用卡寄到相應的用戶家中。

另一方面，從風險控制角度講，風險控制可以分為主動風險控制以及被動風險控制兩種，被動風險控制一般是指，信貸客戶違約后進行的催收行為；主動風險控制則是通過事先的機制確立客戶是否有償還能力以及償還意愿[5]。

在我國，由于征信體系與2013年才開始正式推動以及建立，因此，在此領域屬于起步較晚的國家之一，對于現代交易環境而言，信用體系是一種建立在客戶穩定償還能力上的不用立即支付即可享有相應服務的行為。故風險預測是銀行發放貸款的重要參考之一[6]。

文獻法：本文利用圖書館、網絡以及數字圖書館等資源，搜集關于金融以及機器學習的相關資料相關資料，調查機器學習在金融領域應用的的相關理論，為本文寫作提供理論基礎。

實例分析法：根據模型，對于實際情況進行模擬以及分析，通過對于實際情況的模擬，說明論文的合理性。為該機器學習算法提供現實基礎。

論證法:對于本文用到的相關算法以及部分公式給出推到過程，為本文研究提供數據支撐。

1 數據預處理

將判斷客戶是否有潛在違約風險的數據分為兩個類型，一個為靜態數據類型，其主要包含用戶基本情況以及用戶檢測量表；另一類為動態數據，其主要包含客戶的銀行信息記錄(如流水信息，基本信用信息)，第三方支付記錄等。其中動態信息隨著客戶的時時狀態而發生改變，其具體情況如表1所示。

表1 相關數據資料表

用戶向相關金融機構申請貸款時，需提交自己相關信息，相關平臺利用用戶提供的信息進行建模。如果相關信息缺失，則通過清洗或者變換的形式將所有信息補充完整。此過程預計占用整個工作流程的80%以上的時間，因為整個數學模型的基礎建立在正確的數據處理上，如果相關數據失真，那么整個機器學習進行的最終判定也將會失真。

2 算法比較

1)回歸算法

自從高斯提出最小二乘法以來，回歸分析的應用也越來越為廣泛，在我們日常的生活領域，基本上很難找不用它的領域。自從1969年設立諾貝爾經濟學獎以來，大部分的獲獎者都是統計學家、數學家或者計量學家，獲獎成果也大多與回歸分析相關。

從理論角度看，回歸分析大致可以分為三個階段即理論模型構建、數據采集階段、參數估計與模型校驗階段以及模型應用階段。

本次研究，根據數據特點，可以選用比較成熟的的回歸算法：帶虛擬變量的回歸模型最為本次模型構建。為式(1)。

Y=α1+α2D2i+α3D3i+…+αnDni+βXi+εi

(1)

其中D為虛擬變量，可以表示性別學歷等相關信息，例如D2可以表示性別，當D2=1時，定義為女性；當D2=0時定義為男性。

2)GBDT算法

本次設計采用機器學習算法中比較常見的GBDT算法，其基礎原理為迭代法。具體實施為在迭代過程中，通過改變樣本的權重，學習多個分類其，并且將其進行線性組合，從而提升算法的準確率。

GBDT算法是集成學習算法Boosting下的一個分支學習算法，與傳統學習算法(如Adaboost算法)不同的是，GBDT算法使用向前分布算法，并且使用CATR回歸樹模型進行相關的學習[7]。

其基礎原理為，假設f(x)表示學習器的相關函數，則ft-1(x)表示前一輪得到的強學習器，則損失函數以L(y,ft-1(x))表示，那么最終該算法的目標為，找到弱學習器ht(x)使得損失函數L(y,ft-1(x))=L(y,ft-1(x)+ht(x))最小。

舉例來說，假設銀行有100個實際違約客戶，首先用80個去擬合，發現漏掉20個，這時用12個去擬合剩下的人員，發現還差8個，隨后繼續用8個擬合，知道差距越來越小，每次擬合過程中，都會逐步逼近真實數據，誤差逐漸減小[9]。

3)算法比較

比較帶虛擬變量的回歸算法與GBDT兩種算法，可以看出回歸算法的優勢在于模型建立簡單方便，同時根據銀行所搜集到的數據可以更為方便的增加或者減少相關參數(即D值)，另一方面，從理論角度講，只要參數選擇合理，數據充足回歸算法可以精確的預測出客戶的信用等級，對原始數據要求較高。

相比于回歸算法，GBDT算法相對復雜，但是對于原始數據的要求較低。在科學研究時，一般能夠用簡單方法解決問題時，盡量不用復雜方法但是在實際應用中，銀行因為現實因素，搜集到的客戶信息往往并非十分確切，所以最終根據銀行提供的數據情況來看，選擇后者GBDT算法建立本次模型。

3 算法實現

本文采用的基本機器學習的具體算法為：設集體樣本為最大迭代次數N，損失函數L。最終輸出的學習器為，f(x)。

則初始學習器表示為式(2)。

迭代后(N=1,2,3,4，…，N)有：

1)對于樣本i=1,2,3,…，m的負梯度計算為式(3)。

(3)

2)利用CART回歸樹，得到第N顆回歸樹且對應的子節點區域為，J表示對應回歸樹的葉子節點個數。

3)對于葉子區域計算最佳擬合值。

4)升級版學習器為式(4)。

(4)

故可以得到最終的學習器f(x)表達式為式(5)。

(5)

4 用戶分類以及情景模擬

用戶分類，根據客戶信息以及相關算法信息，可以將客戶劃分為4個類別：

1)本身是信譽客戶，模型判斷也為信譽客戶，記作TN

2)本身是信譽客戶，模型判斷為非信譽客戶，記作FP；

3)本文為非信譽客戶，但是模型判斷為信譽客戶記作作FN

4)本身是非信譽客戶，模型判斷也為非信譽客戶記作TP。

其具體劃分如下表2所示。

表2 用戶類型分類表

故據此可以計算該模型的準確率TPR:

模型錯誤率FPR:

故現有基本特征如下的銀行客戶樣本：

1)如果用戶信用記錄有超過60天逾期行為，則記作Y=1；否則記作Y=0；如某銀行內有50 000名客戶，而逾期的用戶為3 000名，且3 000名非信譽用戶符合隨機分布原則。

2) 用戶信息：特征時間主要包含用戶所有的動態信息，其中包含前文提及的銀行流水記錄以及金融信息記錄。同時也包含用戶檢測3個量表的相關結果均已經處理齊全。

方案A，將所有貸款申請用戶平均分為10組，每組5 000人，且每組包含300個非信譽客戶；

方案B，根據模型可以計算的用戶違約概率，將每個用戶違約的概率記作P，則根據P值，將客戶從大到小順序，然后分成十個組，每組5 000人。顯然十組中，靠后的分組里，信譽用戶明顯占優更多比例，而非信譽客戶則在第一種最多。故此時只要尋找到，P值的分界點，即可確立最終的放款條件。其具體數據如表3所示。

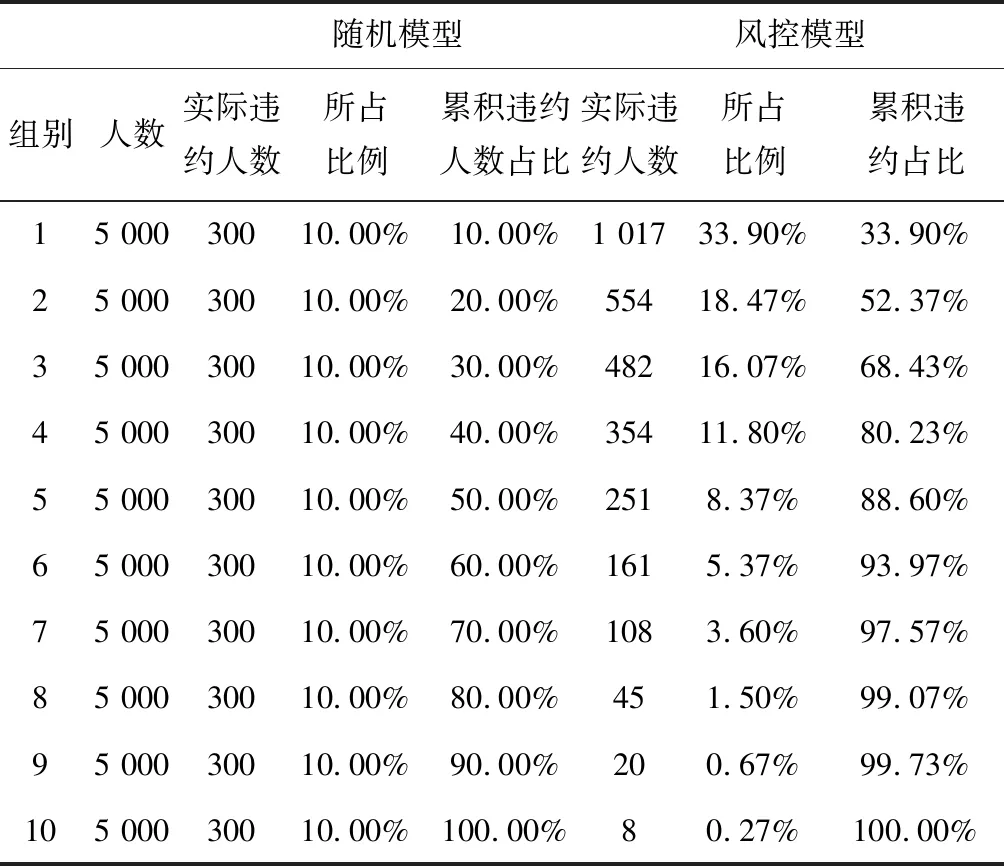
表3 隨機風控模型對比表

5 模型評價

將A、B兩組每一組的非信譽客戶的所占比重繪制成提升圖，如圖1所示。

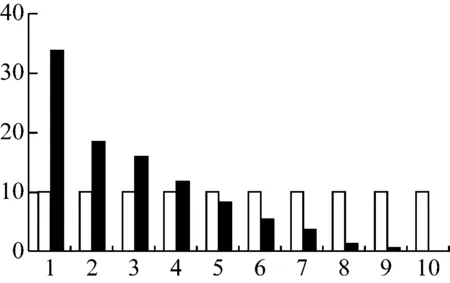
圖1 提升圖

從圖中可以看出，方案B中，每組的非信譽客戶人數在逐步遞減，則該模型具有一定的現實意義，模型有效。

此時再根據前文提到的模型準確率(FPR)以及模型錯誤率(TPR)相關概念，由于模型計算結果以及真實結果均為已知，故可以輕松算得FPR,TPR兩個參數。故以FPR為橫軸，TPR為縱軸繪制ROC曲線。如圖2、圖3所示。

根據洛倫茲曲線的判定公式，此時選用ROC曲線常用衡量性能指標AUC來表示，AUC曲線通過計算ROC曲線下面積而求得，一般來說，AUC的值在0～1之間，本文中顯然方案A的AUC值為，0.5；而方案B的AUC通過計算可以得知，其值為0.74.一般來說，一個模型AUC值要大于0.5才會具有實際效果，AUC值在0.7～0.9之間則被認為是一個優秀模型；AUC高于0.9，則認為該模型有異常變量進入，導致AUC過高。

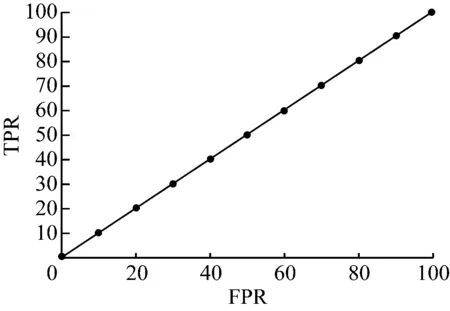
圖2 方案A ROC曲線

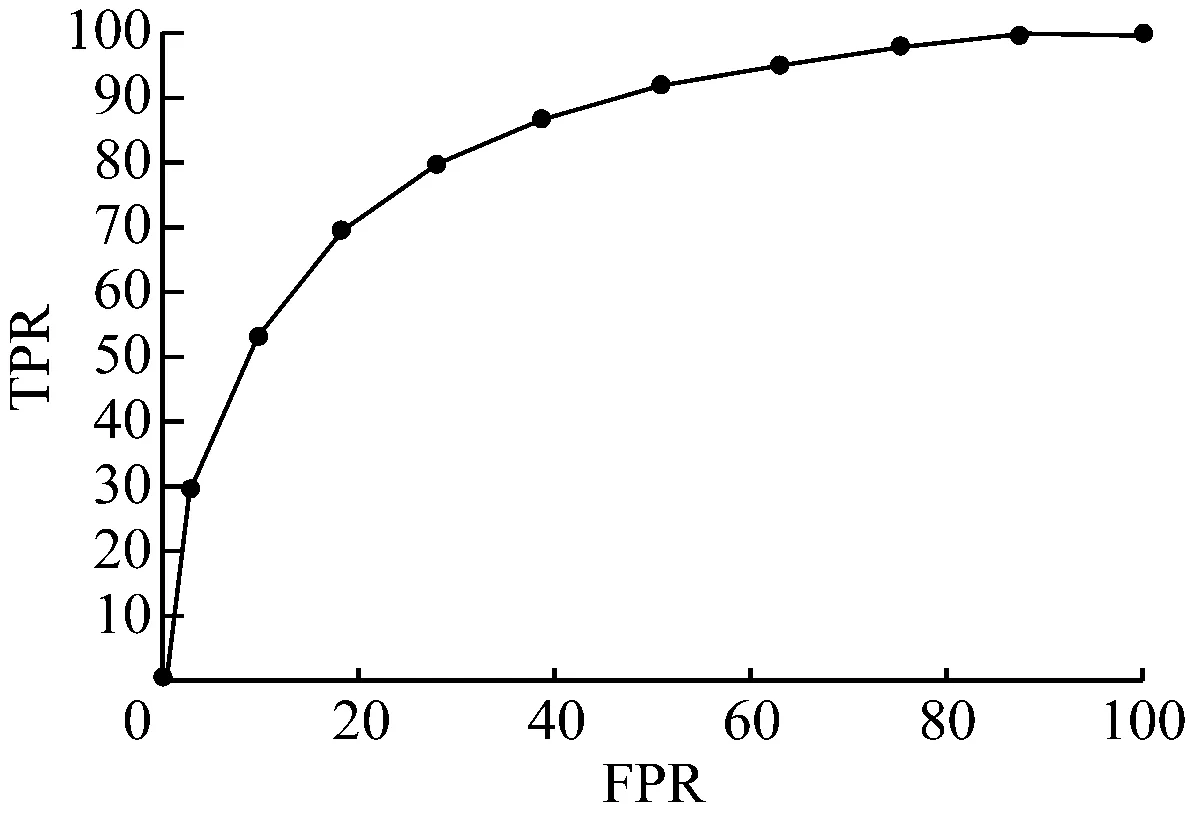
圖3 方案B ROC曲線

而本次模型的最終AUC值為0.74，故符合相關要求，屬于優秀模型范疇。

6 總結

本文針對互聯網金融行業的信用風險問題，利用機器學習算法構建了一個信用風險預測模型，該模型的創新點在于首先數據處理方面，除了應用傳統的用戶基本信息、銀行流水記錄、金融信息記錄外，還引入了用戶用戶檢測量表的相關數據，次量表評定標準以及在模型中所占比重只有系統以及銀行系統以及高層管理人員掌握，從一定程度上避免了人為因素對于放款的影響。由于此部分不是本文重點，故不做詳細說明。

機器學習方面，本文選用傳統的GBDT算法，對于用戶的違約概率進行預測，最后通過相關實例進行說明。

但是由于筆者能力有限，文章亦有一定的局限性，例如論文實例部分假設過于理想化，所有數據均已處理完善，但是實際情況可能會出現相應的數據不足，需要進行缺失數據的處理，由于篇幅有限并未給出相關算法。