某下穿鐵路U形槽結構設計及數值分析
宋志剛
(中鐵工程設計咨詢集團有限公司太原設計院,山西太原 030000)
當前,在公路、鐵路及市政道路等工程建設中,出現了大量的下穿立交工程[1]。在地下水位較高或地下水豐富的地區,U形槽結構得到了廣泛應用。U形槽結構主要通過邊墻抵抗墻背壓力,通過結構、附屬設施自重抵抗浮力,通過底板、邊墻阻止本體外地下水的侵入,從而保證結構的穩定性和耐久性[2]。
目前,U形槽結構分析的主要方法有解析法與數值法。解析法是將結構邊墻和底板分開計算,邊墻按照浸水地區懸臂擋墻考慮,底板按照彈性地基梁(梁與地基共同作用)考慮[3-5];但其未能考慮U形槽結構的整體抵抗荷載能力,不能直接算出結構各位置的變形、位移,具有一定的應用局限性。數值方法能夠較全面地模擬分析U形槽結構各工況下的受力、變形情況,克服了傳統分析方法的不足[6-9],以下擬通過數值分析研究,總結U形槽結構位移變形、地基反力及結構彎矩的變形規律,對比分析其與解析方法的異同。
1 工程概況
該工程位于既有南同蒲鐵路,為平交道口改下穿立交工程。引道走向與鐵路一致,西側引道外為某改移省道,公路外側為汾河河灘,東側引道外為某煤礦職工生活小區。
1.1 工程地質和水文地質
該工程位于汾河河漫灘之上,地形較為平坦,地面高程約為532.1 m。主要地層有:①填筑土(Q4ml),中密,稍濕,成分以砂質黃土及碎石土為主,厚2~3 m;②黏質黃土(Q4al),硬塑,層厚0.8~3.1 m;③細圓礫土(Q4al+pl),中密,稍濕-飽和,層厚5.8~10 m。
地下水以松散巖類孔隙水為主,屬潛水。地下水穩定水位為524.15 m。場地位于汾河河漫灘,臨近汾河主河道,地下水位受河水影響較大,考慮到季節變幅、汾河洪流等綜合因素的影響,地下水位變幅取523.15~526.65 m。
1.2 槽體尺寸
因地下水位高于下穿段路面設計高程,故引道部分地段設U形槽進行防護。結構底面凈寬9.25 m,底板寬13 m,厚1.2 m;邊墻高7.5 m,頂面寬0.4 m,內側豎直,外側邊坡坡率為1: 0.20。公路路面寬8.0 m,為雙車道設計,機動車路面采用C25素混凝土墊層,厚0.4 m,人行道寬1.25 m,結構橫斷面示意見圖1。

圖1 U形槽結構橫斷面(單位:m)
1.3 結構參數
(1)結構采用C35混凝土,容重γ=25 kN/m3,
(2)路面墊層厚度為0.4 m,采用C25混凝土澆筑,容重γ=23 kN/m3;右側人行道采用C25混凝土鋪設,高出路面0.2 m,寬1.25 m,容重γ=23 kN/m3。
(3)根據《公路橋涵設計規范》[10],車輛荷載標準值取后軸軸載(140 kN),按集中力考慮;車輛荷載立面、平面尺寸參照《公路橋涵設計規范》之圖4.3.2-1;人群荷載標準值取3.0 kN/m2,均布作用在人行道上。
(4)墻后回填黃土及部分圓礫,內摩擦角φ=30°,填土與墻背摩擦角δ=φ/2=15°,容重γ=18 kN/m3,飽和容重γsat=20 kN/m3。
(5)墻底置于細圓礫土層,地基基本承載力容許值fa0=500 kPa,墻底摩擦系數為0.4。
(6)邊墻背側設計低水位為9.0 m(距墻頂),設計高水位為5.5 m(距墻頂)。
2 U形槽設計及驗算
2.1 計算模型選取
針對U形槽結構特點,取縱向單位長度進行簡化計算[11]。邊墻按一般剛性懸臂式擋土墻考慮,主要承受側向土壓力、水壓力荷載,按受彎構件進行內力及配筋計算[12];底板按彈性地基梁考慮,主要荷載包括結構自重、浮力、墊層自重、邊墻傳遞荷載及機動車人群活載等[1]。另外,其結構尺寸還應滿足抗浮及地基承載力的驗算要求。
2.2 抗浮驗算
進行抗浮穩定性檢算時,設計水位應采用最高水位,抗浮荷載只計主體結構自重。抗浮穩定安全系數為主體結構自重與所受浮力的比值,其值不應小于1.05[2],其計算公式為
(1)
式中,Gk為結構自重/kN;Flk為結構主體所受浮力/kN;γ為荷載分項系數,一般取0.9。
對于本工程,主體結構自重為968.01 kN,所受浮力為411.08 kN,Kf=2.35,滿足設計要求。
2.3 地基承載力驗算
一般情況下,U形槽結構自重小于與其同體積的原狀土自重,地基承載力能夠滿足設計要求。當地基為軟土層時,應進行地基承載力驗算。檢算時采用設計低水位,考慮車輛和人群活載作用[13],檢算公式為
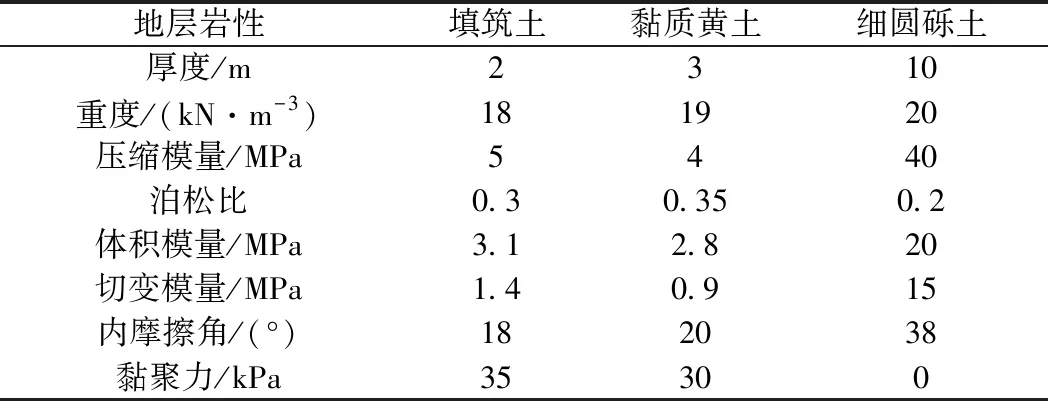
Pz 式中,Pz為底板底面地基附加應力值/kPa;faz為底板底面經深度修正后的地基承載力特征值/kPa。 經計算,該U形槽底板底面附加應力值為96.3 kPa,遠小于修正后的地基承載力特征值(654 kPa),地基承載力滿足要求。 邊墻按懸臂式擋土墻考慮,并采用設計高水位(設計低水位一般不具控制作用)。邊墻荷載主要包括邊墻自重,邊墻墻背土、水壓力[11]。邊墻自重按初步擬定尺寸計算,墻背土壓力和水壓力一般采用“水土分算”和“水土合算”兩種方法。對于黏性土等滲透性較弱的土質采用“水土合算”,對于砂土等滲透性較強的土質采用“水土分算”[14]。另外,由于結構與土體基本無相對位移,可采用靜止土壓力形式進行計算[15]。 根據上述設計方法,對邊墻進行受力分析,其彎矩及剪力如圖2所示。 圖2 邊墻彎矩及剪力 根據內力計算結果,對邊墻進行截面抗彎、抗剪強度檢算和裂縫寬度驗算。最終確定邊墻外側受拉鋼筋選用φ25@100,內側受壓鋼筋選用φ12@100,箍筋選用兩肢φ14@200。裂縫寬度0.043 mm<0.2 mm,滿足規范要求。 底板按彈性地基梁(梁與地基共同作用)考慮,其承受荷載包括結構自重、浮力、端部彎矩、車輛及人群活載等。邊墻底部截面的彎矩(作為集中彎矩荷載)施加在兩者連接處(按剛性連接考慮)[11]。車輛及人群活載參考《公路橋涵設計規范》[10]取值,車輛荷載應按作用在最不利位置處考慮,并按該工況對底板進行強度計算。底板的計算荷載組合應考慮各種外力的最不利組合,一般為四種情況:設計低水位有活載、設計高水位有活載、設計高水位無活載、設計低水位無活載(不具控制作用)。 對前三種荷載組合下的底板內力進行計算(車輛活載按圖5位置施加),內力值:高水位無活載>高水位有活載>低水位有活載。 高水位無活載工況下底板內力如圖3所示。根據受力情況,進行底板抗彎、抗剪強度檢算及裂縫寬度驗算。根據檢算結果配筋如下:底板下部縱筋選用φ30@100,上部縱筋選用φ18@100,箍筋選用兩肢φ12@200。 圖3 底板彎矩及剪力 利用FLAC3D軟件的有限差分法進行數值模擬分析。取沿引道方向單位長度1 m進行分析研究,地基本構采用Mohr-Coulomb模型[16],地基模型寬100 m,深50 m,縱向長1 m。地基位移約束情況為:底面固定、頂面自由,側面約束法向位移[6]。地下水采用孔隙水壓力模擬,U形槽結構采用襯砌(Liner)單元模擬。根據結構實際尺寸,對邊墻、底板進行不同襯砌厚度賦值。土層計算參數見表1,襯砌結構單元參數見表2,結構模型見圖4。 表1 土層計算參數 表2 U形槽結構單元(襯砌結構單元)參數 圖4 U形槽結構模型 按照三種荷載工況對U形槽結構進行數值分析。恒載主要包括U形槽結構自重、浮力、墊層重力及人行道重力,活載主要為車輛荷載及人群荷載。荷載工況主要分為低水位有活載、高水位有活載與高水位無活載三種,活載施加位置見圖5。 圖5 U形槽活載施加位置 數值結果分析主要包括槽周土體位移、地基反力及槽身彎矩。 (1)槽周土體位移分析 各荷載工況下槽周土體位移見圖6。 三種荷載工況下槽周土體位移呈現以下特征: ① 邊墻土體位移普遍較底板位移小,尤其在水位以上的部位。三種工況下,低水位有活載時位移較大,高水位無活載時次之,高水位有活載時最小。由圖6可知,水位對邊墻土體位移影響較大,活載對邊墻位移影響較小。 ② 三種工況下,底板土體位移均向上呈馬鞍形分布,中部較大,兩側較小。三種工況下,底板土體最大位移均在2 mm左右,相差不大,說明活載及水位對底板土體位移的影響主要體現在位移分布形狀上,對位移數值影響較小。 (2)地基反力分析 三種荷載工況下地基反力見圖7。 圖6 槽周土體位移(單位:m) 注:FLAC3D規定壓應力為負值。圖7 地基反力(單位:Pa) 圖8 結構彎矩(單位:N·m) 三種荷載工況下地基反力有以下特點: ①邊墻地基反力自上而下隨深度增加而增大,同時,下部較上部的地基反力變化率也較大。三種荷載工況下,邊墻同一位置處地基反力數值相近。 ②三種工況下底板地基反力變化規律相同,由邊墻至底板中心呈馬鞍形分布,在大致距邊墻1/4底板長度的位置達到最大值。由邊墻至底板中心,反力變化速率由急劇趨于平緩。三種荷載工況下,低水位有活載時反力較大,高水位有活載時次之(與無活載時相差不大),高水位無活載時最小。說明底板地基反力值隨水位深度增加而增大。 (3)結構彎矩分析 三種荷載工況下結構彎矩見圖8。 三種荷載工況下結構彎矩有以下特點。 ①邊墻彎矩自上而下數值增大,且下部變化較為顯著,最大值出現在墻底與底板交界處。三種荷載工況下邊墻彎矩變化趨勢一致:高水位無活載>高水位有活載>低水位有活載,表明水位及活載對邊墻彎矩均有影響。 ②底板彎矩最大值出現在邊墻及底板跨中位置,邊墻彎矩為負,底板跨中位置為正,零彎矩點出現在邊墻至跨中1/3距離處。三種荷載工況下,高水位無活載時最大正彎矩值最大,低水位有活載時次之,高水位有活載時最小。 數值分析中,認為槽周土體變形等同于結構變形。數值分析是將整個結構作為整體進行計算,可以直接得到結構的變形值。而解析法將邊墻、底板分開考慮,無法得到結構各位置的變形值。 三種荷載工況下,兩種方法地基反力如表3所示。 表3 U形槽地基反力分析結果 kPa 通過對表3的分析可知: (1)對于邊墻地基反力,兩種方法結果較為接近。解析方法中邊墻地基反力與水位有關,而與荷載無關,而數值分析結果顯示,邊墻地基反力與荷載有弱相關,但影響極為輕微,可忽略不計。 (2)對于底板地基反力,二者變化規律基本一致,但數值相差較大(數值方法要大于解析方法)。三種工況下,底板同一位置處,解析算法得到的地基反力變化較大,而數值分析得到的地基反力變化較小。究其原因,數值分析方法將整個U形槽結構體視為一個剛性整體,整體剛度較大,地基反力較小。而解析算法將底板單獨考慮,在水位及荷載作用下產生的地基反力就較大。 三種荷載工況下,兩種方法結構彎矩如表4所示。 表4 U形槽結構彎矩分析結果 kN·m 通過對表4的分析可知: (1)解析方法的邊墻彎矩較數值分析方法普遍較小。解析方法中邊墻彎矩與水位有關,而不考慮底板荷載的影響;而數值分析方法結果顯示,邊墻彎矩不僅與水位有關(高水位工況數值大于低水位工況數值,與解析方法趨勢一致),并且隨著底板活載的施加而減小。兩種分析方法的差異主要在于解析方法將邊墻單獨作為懸臂墻計算,而數值分析方法將邊墻、底板作為整體計算(考慮了底板荷載對邊墻內力的傳遞)。 (2)兩種方法得到的底板彎矩變化規律基本相同,基本呈馬鞍形分布,底板彎矩最大值均出現在邊墻及底板跨中位置。不同的是,解析算法中邊墻與底板跨中位置彎矩值符號相同,而數值分析方法中則恰好相反。這說明二者的數值差異較大,分析其原因:數值分析將底板與邊墻作為剛性體整體計算,而解析算法僅僅考慮了邊墻荷載對底板的傳遞,并未考慮邊墻在底板抵抗荷載時的協同作用。 (1)U形槽結構解析計算時,邊墻按一般懸臂式擋土墻考慮,底板按彈性地基梁考慮(彈性半空間無限體模型)。另外,U形槽結構的尺寸應滿足抗浮及地基承載力要求。 (2)在結構地基反力、彎矩方面,解析方法與數值分析方法變化規律一致,由于兩種分析方法計算模式的不同(數值分析方法將邊墻與底板作為整體計算,而解析方法則將二者分離計算),其數值相差較大,還需進一步進行試驗論證。2.4 邊墻強度計算
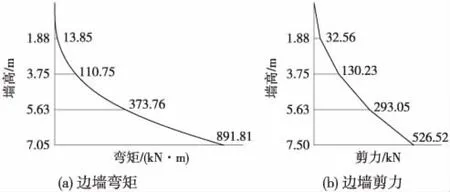
2.5 底板強度計算

3 數值分析
3.1 結構建模及參數


3.2 荷載施加

3.3 結果分析



4 數值分析與解析方法對比分析
4.1 結構變形
4.2 地基反力
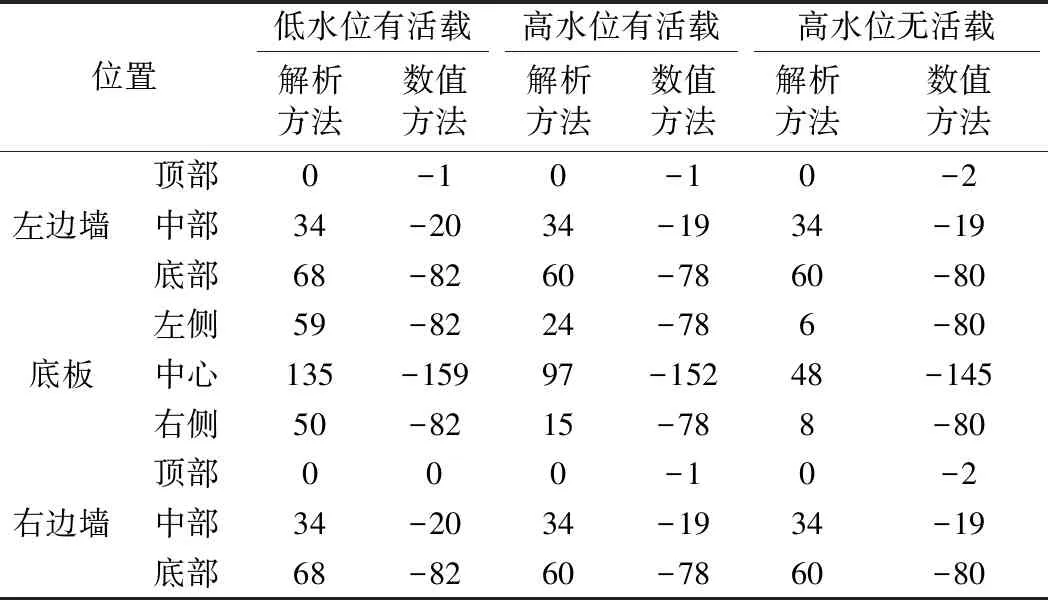
4.3 結構彎矩
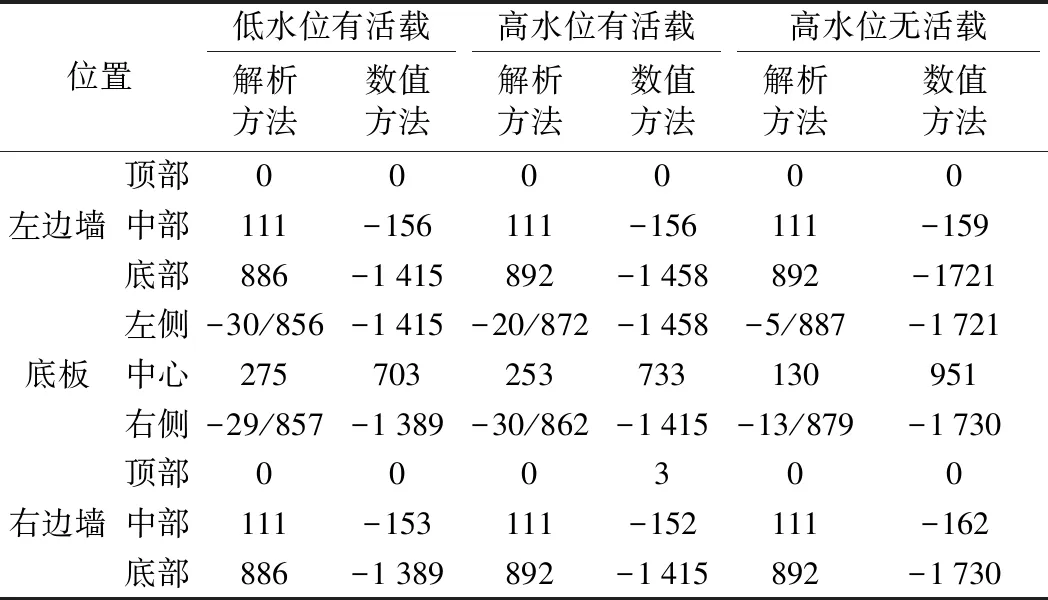
5 結論

