基于性能的高速鐵路鋼管混凝土拱橋地震經濟風險分析

馮莉，樊燕燕，王力，李子奇, 2

?

基于性能的高速鐵路鋼管混凝土拱橋地震經濟風險分析

馮莉1，樊燕燕1，王力1，李子奇1, 2

(1. 蘭州交通大學 土木工程學院，甘肅 蘭州 730070； 2. 蘭州交通大學 道橋災害防治技術國家地方聯合實驗室，甘肅 蘭州 730070)

在基于性能的地震風險評價理論基礎上，以一座高速鐵路鋼管混凝土系桿拱橋為例，采用有限元分析軟件建立全橋模型，運用增量動力分析(IDA)方法對該橋拱肋進行地震易損性分析，建立關鍵截面的易損性曲線，結合地震危險性和損失比，選取年預期損失作為地震經濟風險指標，定量分析該橋的地震經濟風險。研究結果表明：IDA方法用于鋼管混凝土拱橋的地震經濟風險分析是可行的，該橋主要經濟風險來源于超越概率較高的中小級別地震，占橋梁整體經濟風險損失的77.3%，通過對易損區域的局部加固設計，在提高橋梁魯棒性的同時可減小結構的地震經濟風險。

高速鐵路；系桿拱橋；增量動力分析；易損性曲線；地震經濟風險

橋梁作為生命線工程，是交通線路的重要樞紐，其抗震能力對道路交通的地震安全性具有重要影響。近幾十年來的震害調查和統計分析表明，橋梁結構的破壞會給經濟帶來不貲之損。因此，將基于性能的結構抗震理論應用于橋梁地震經濟風險評估，預計不同強度的地震對橋梁結構破壞程度及其可能造成的經濟損失具有極為重要的意義。國內外研究者對基于性能的抗震評估進行了一系列的研究，但始終無法確定一個統一的標準，致使不同工程結構的評估方法也各異。單從工程參數解釋結構抗震性能并不能被所有利益相關者理解，但用定量的經濟指標描述橋梁的地震風險，便可使非工程技術的利益相關者能夠更容易地理解結構的地震經濟風險。國外對于橋梁基于性能的抗震理論和評估方法研究較早，2000年Cornell等提出太平洋地震工程(PEER)基于性能的概率理論公式[1]，并在2002年給出PEER基于性能的概率理論基礎[2]。2003年， PEER提出了基于性能的抗震評估理論，主要基于全概率理論考慮了結構的非線性行為和地震作用的不確定性，從經濟角度考慮結構抗震性能問題[3]。目前基于全概率的PEER理論在國內的研究相對匱乏，且主要集中于框架結構的地震風險分析，而對于橋梁結構的相關研究極少。羅文文等[4]以基于全概率的PEER方法為基礎，結合地震損失計算方法和流程，歸納總結了RC框架結構各類構件的易損性函數和損失函數，定量評價地震損失。韓建平等[5]也借鑒PEER提出的單體建筑基于性能的損失評估理論，對RC框架結構進行增量動力分析，進而得到不同損傷狀態的易損性曲線，并在此基礎上進行了地震直接經濟損失的分析。ZHANG等[6]針對一座高墩大跨連續剛構橋，根據橋墩損傷狀態研究成果建立解析損傷脆弱性函數，用定量經濟指標描述橋梁地震經濟風險。截至目前，針對鋼管混凝土拱橋的地震經濟風險研究還未見報道，因此，本文在國內外研究成果的基礎上，運用基于性能的地震風險評價理論，以高速鐵路線上一座典型的鋼管混凝土系桿拱橋為研究背景，分析該類橋的地震經濟風險，為開展相關研究工作奠定基礎。

1 地震經濟風險評估理論

美國PEER提出的基于性能的地震風險評估理論[7]中，將評估過程分為4個階段，即：地震危險性分析、工程結構分析、損傷分析和損失分析。本文在PEER性能評估框架方法的基礎上，以年預期損失(EAL)作為地震經濟風險的評價指標，采用Dhakal和 Mander提出的年預期損失(EAL)公式[8]：

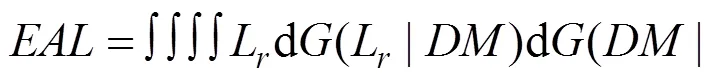
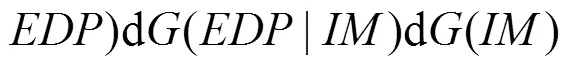
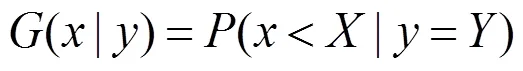
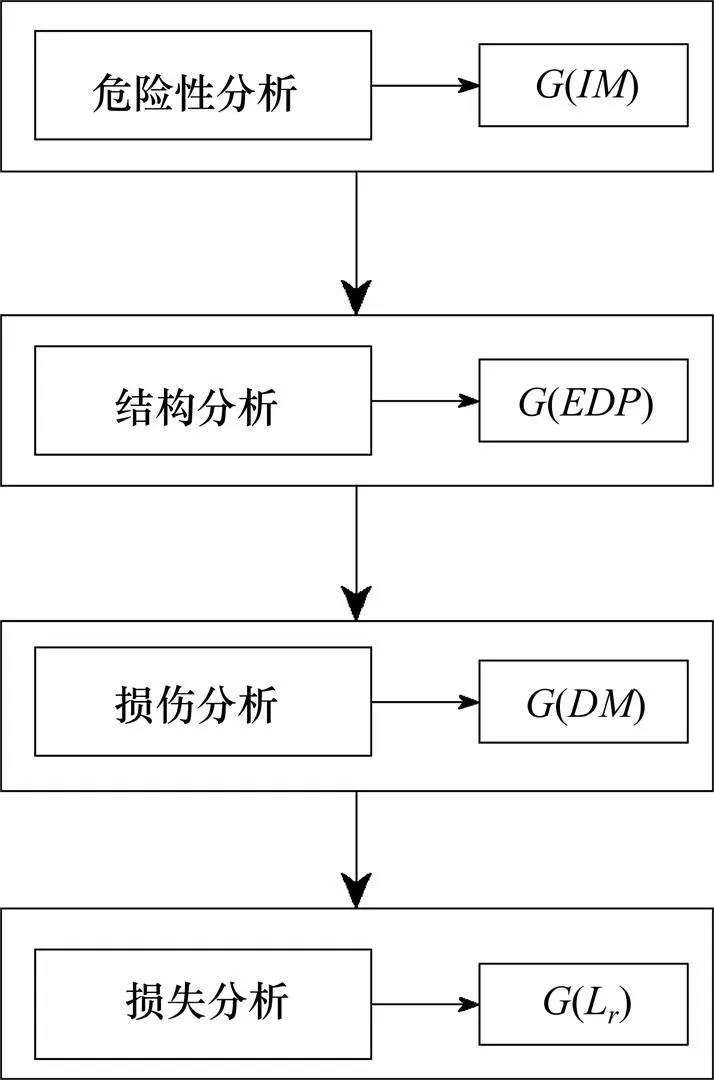
圖1 分析流程圖

1.1 地震危險性分析

地震危險性是指在一定時間內，城市或工程建筑物所在場地可能遭遇地震作用的大小和頻次。通過地震危險性分析，可以得到地震運動強度指標和年平均超越概率(a)的地震危險性曲線。本文采用Cornell等[2]提出的用概率論方法對地震危險性進行估計的計算方法，用于描述地震強度指標(IM)與年平均超越概率(a)的關系，計算公式如下：

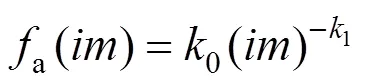
式中：a為地震年發生頻率；0和1均為經驗常數。

1.2 結構分析

目前，地震易損性分析一般采用非線性動力分析法。非線性動力分析法又可分為極大似然估計法、云圖法和IDA法等。為了確定結構在不同地震危險水平和特征下的動力響應，本文采用IDA方法，通過等比例調幅法得到一系列不同強度的地震動記錄，并逐次對結構進行非線性時程分析，最終可得到多條地面強度指標(IM)與工程需求參數(EDP)的關系曲線[9]，即IDA曲線簇。

對于多條IDA曲線形成的IDA曲線簇，不便得到結構在設防水準下的位移能力，故需對IDA曲線簇進行統計分析。常用的分析方法有參數方法和非參數方法，本文采用目前應用較多的非參數統計方法，該方法可直接求得某一地震強度下的EDP中值(50%)和16%，84%分位數值，其中，50%分位曲線表示EDP的平均水平，16%和84%分位曲線表示EDP的離散程度，計算公式如下：

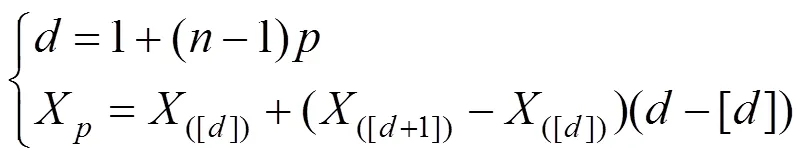
式中：為百分位數X所在位次；[]為的整數部分；([d])，([d+1])分別為[]和[+1]上的值。

1.3 易損性分析

通過IDA方法可得到結構的關鍵截面IDA曲線，然后運用理論易損性分析法，將不同地震波作用下的曲率延性比和各個損傷狀態對應曲率下的損傷指標相比，并對得到的離散數和不同峰值加速度建立對數函數，最后運用式(4)計算結構在各個破壞階段的超越概率，便可得到結構的易損性曲線[10]。

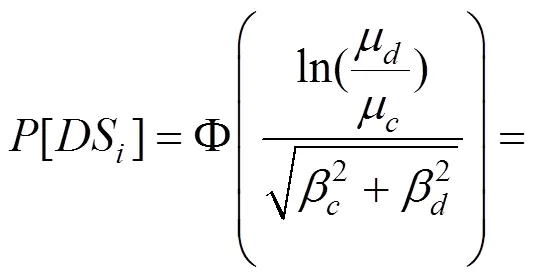
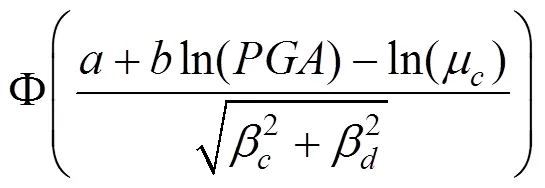
1.4 地震經濟風險分析

通過數值積分，年預期損失風險計算式(式(1))可以用更具有實用性的離散形式來表示：

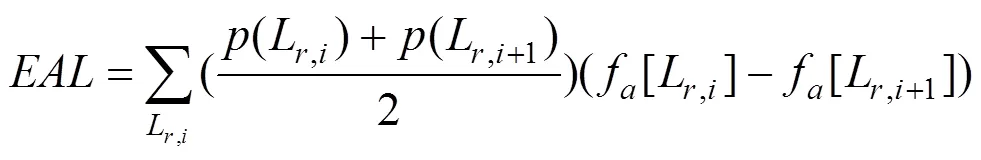
參照中國地震局頒布的《災害直接損失評 估》[11]中規定的橋梁破壞損失比，將損傷狀態劃分為5個等級：基本完好(1)、輕微破壞(2)、中等破壞(3)、嚴重破壞(4)和完全破壞(5)。得到不同損傷狀態下對應的橋梁損失比取值，如表1所示。由于鋼管混凝土系桿拱橋一旦發生嚴重破壞，結構雖未完全倒塌，但修復難度極大，本文假定在該損傷狀態下維修加固費用與重建費用相等，即設定損失比取為1.0。

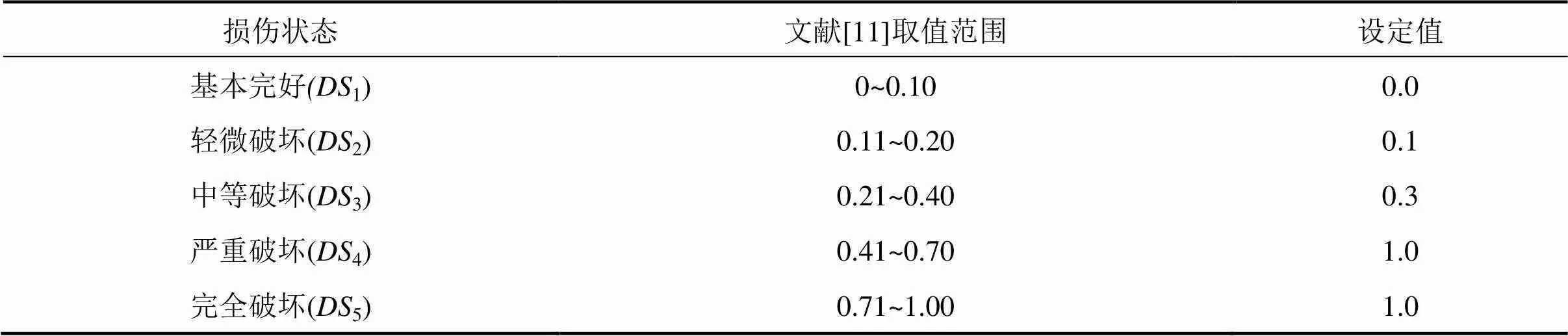
表1 各損傷狀態對應的損失比Lr

2 工程概況及模型建立

該高速鐵路鋼管混凝土系桿拱橋位于寶蘭客專線上，橋長0=100.316 m，橋跨為1孔80 m的鋼管混凝土系桿拱，拱軸線為二次拋物線，矢跨比/=1/5，矢高=16.0 m。

運用MIDAS/Civil軟件建立該橋有限元模型，主梁為箱梁截面形式，采用空間梁單元模擬；為方便劃分纖維截面，采用2個單圓管截面模擬啞鈴型鋼管混凝土截面，兩單圓管間采用剛性連接，吊桿采用桁架單元模擬，梁端支座采用固定和活動約束模擬，橫撐與K撐用空心鋼管梁單元模擬。全橋有限元模型如圖2所示。

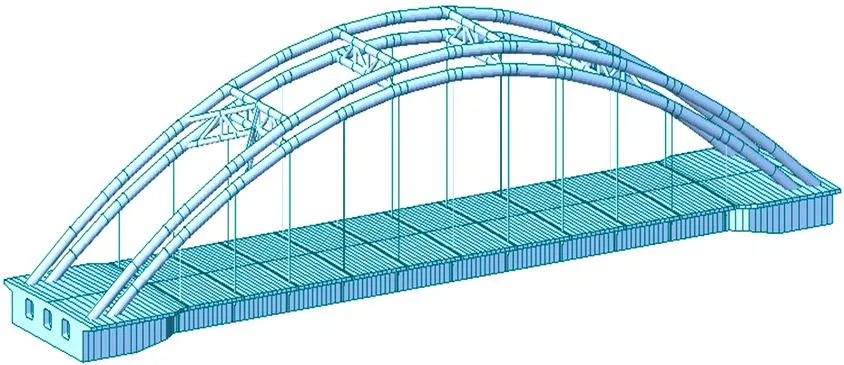
圖2 鋼管混凝土系桿拱橋有限元模型

運用Rayleigh-Ritz法對全橋空間有限元模型進行自振特性分析，分析表明：當振型到第105階時，順橋向、橫橋向和豎橋向振型累計參與質量均達到99%以上。限于篇幅，本文僅列舉全橋前12階主要振型，如表2所示。

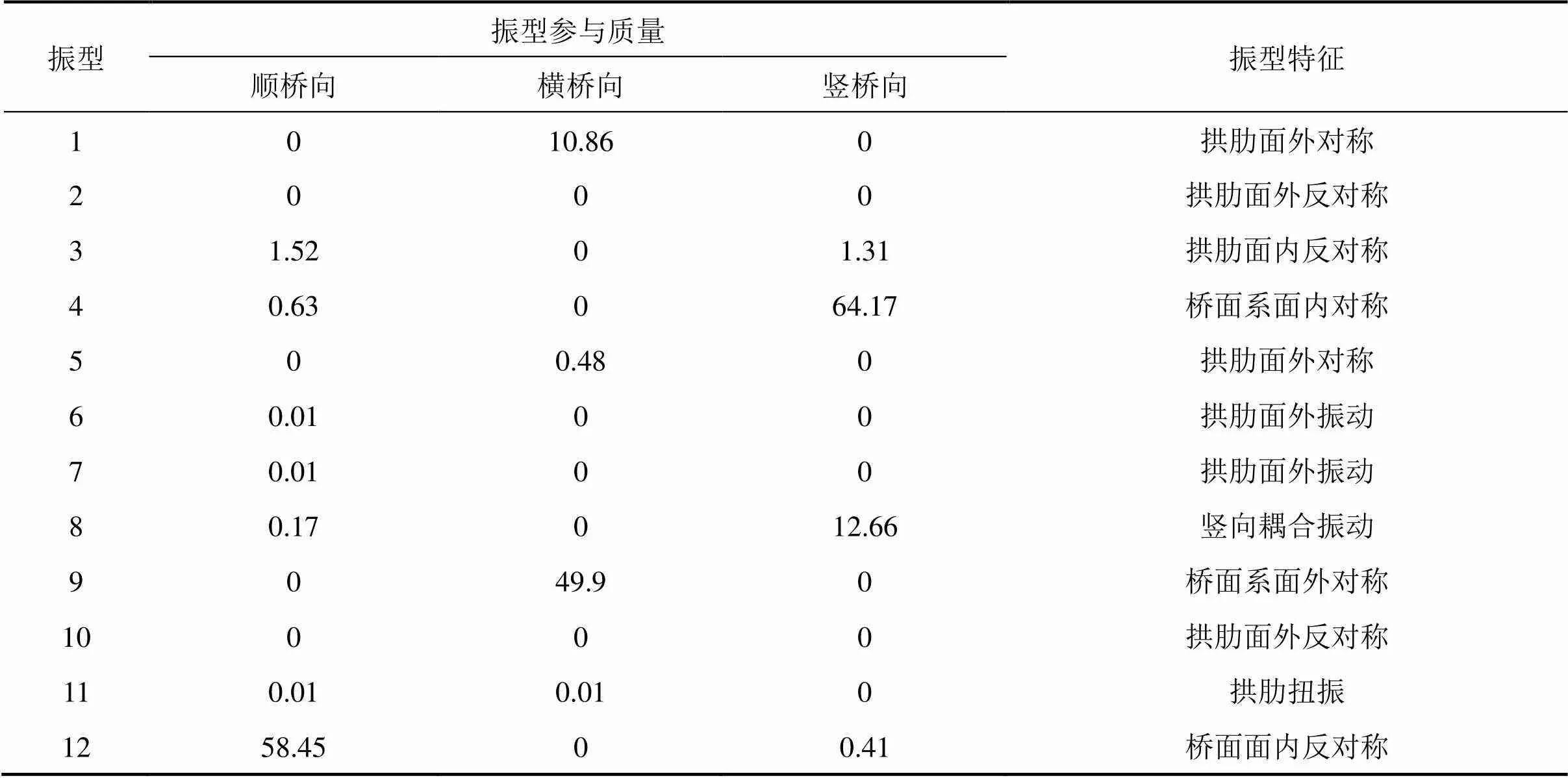
表2 拱橋自振特性

由表2可得：1) 該橋的橫橋向振動分拱肋振動和橋面系振動，第1階振型表現為拱肋橫向漂移，表明相對于橋面系，鋼管混凝土拱肋橫向剛度較小；2) 豎橋向、橫橋向和順橋向主振型分別出現在第4階、第9階和第12階，振型參與質量占比分別為58.45%，49.9%和64.17%；3) 拱肋的扭轉振動在第11階才出現，表明該橋整體抗扭剛度較大。

3 結構分析

3.1 地震危險性設定

根據鐵路工程抗震規范[12]規定的相應抗震設防標準，多遇地震、設計地震和罕遇地震年平均超越概率分別為0.02，0.002 1和0.000 4。該橋場地類型為Ⅱ類場地3區，地震設防烈度為8度，場地特征周期為0.45 s，設計地震峰值加速度為0.2。采用地震危險性計算公式(2)，利用其中2個地震強度和相應的地震動峰值加速度可確定式中的待定參數0和1，經計算得：0=5.013×10?5，1=2.296 1，最后擬合得到地震危險性曲線，如圖3所示。由該曲線可得任意地震危險性對應的地震峰值加速度(PGA)。

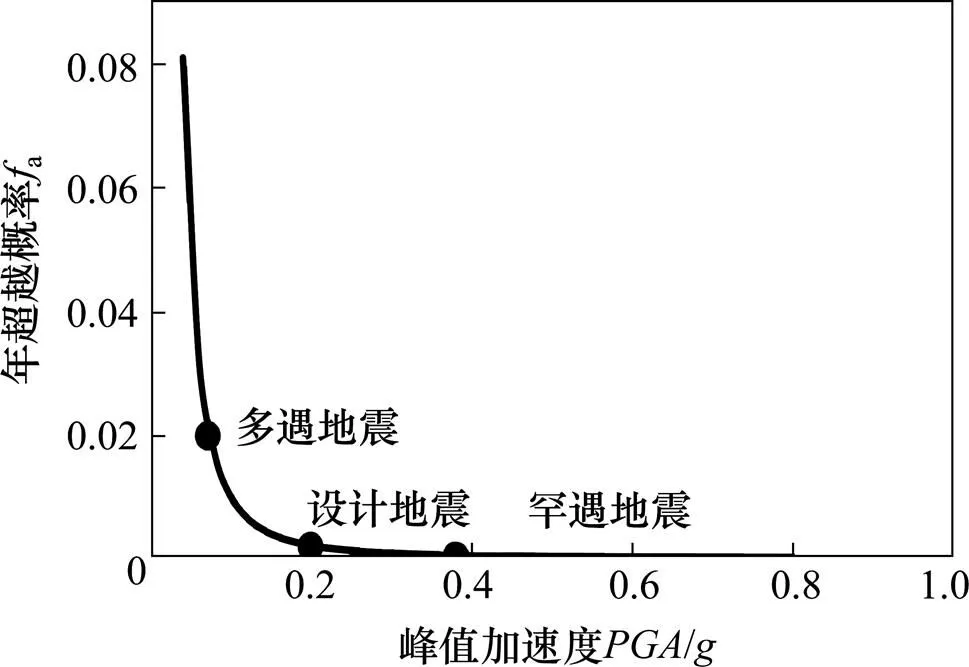
圖3 地震危險性曲線

3.2 增量動力分析(IDA)

從PEER選取20條與橋址處場地條件相同的地震動記錄，對該橋進行IDA分析。基于以上選擇的20條實際地震動記錄，以0.05為幅值從0.1~2.0逐條等比例調幅，對結構進行動力彈塑性分析[13?14]。為了得到拱肋在抗震性能評估中的控制截面，選取調幅后=0.2的EL-Centro波進行對比分析，計算結果如表3所示。

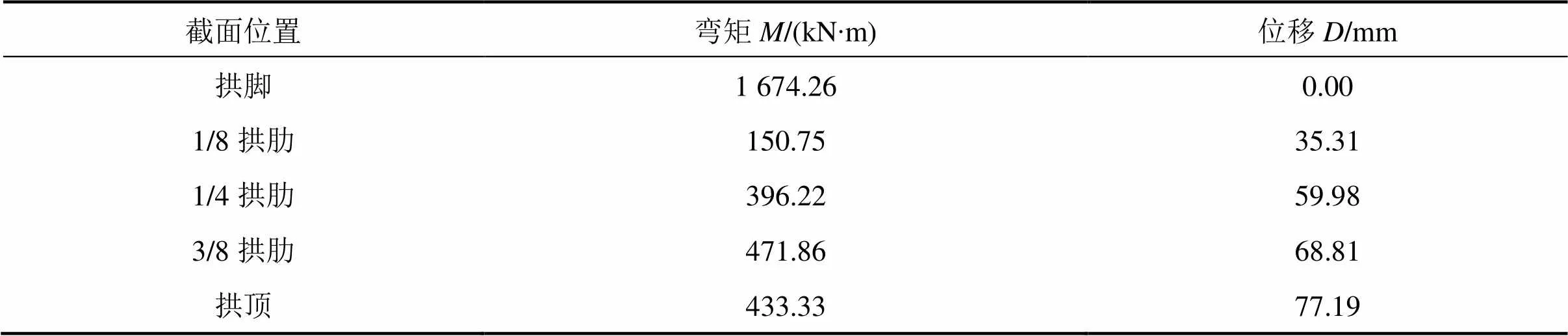
表3 關鍵截面內力、位移對比(PGA=0.2g)

由表3可得，該橋內力峰值出現在拱腳區域，位移峰值出現在拱頂位置。另外，由于拱肋橫撐的存在，使得1/4拱肋至拱頂位置處整體強健性較好，在地震作用下能夠保持良好的工作狀態，故以拱腳位置作為控制截面，對該橋進行抗震性能分析和評估。以作為IM參數，橫橋向最大位移max作為EDP參數，建立拱腳截面的IDA曲線簇和分位曲線，如圖4所示。

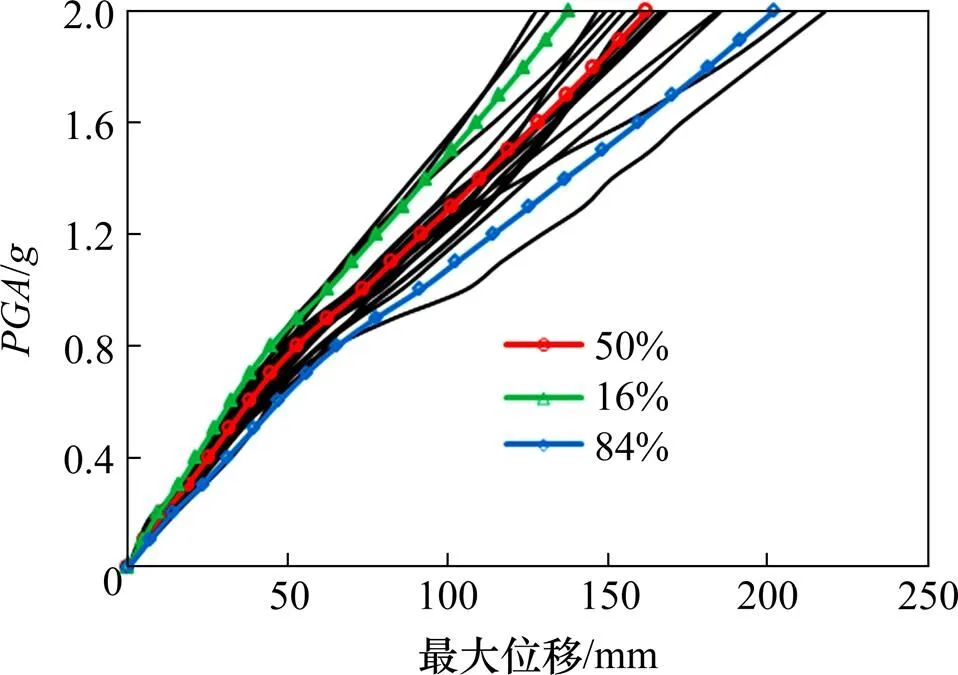
圖4 拱腳IDA曲線

綜合圖4中IDA曲線簇和分位IDA曲線可知：1) 當≤0.2時，曲線基本呈直線增長，截面處于彈性工作狀態；當0.2＜≤0.8時，曲線出現了一定離散性，這是由于在地震動強度逐漸增大時，鋼管混凝土拱肋核內混凝土有部分出現屈服，但鋼管仍處于彈性工作狀態，滿足截面正常受力；當＞0.8時，鋼管局部逐漸進入屈服，曲線離散度逐漸增大，直至全截面破壞。2) 當＜0.8時，拱腳50%、16%和84%分位IDA曲線很接近，說明結構離散度很小，據此表明結構剛度較大，在設計中偏于保守；當≥0.8時，拱腳50%，16%和84%分位IDA曲線出現“折角”，離散度逐漸增大，表明結構由于地震動強度增大時，拱肋進入非線性工作狀態，截面剛度逐漸減小。

4 經濟風險分析

4.1 損傷級別劃分

本文以鋼管混凝土拱肋曲率延性比作為結構損傷狀態的量化指標[15]；對拱腳截面進行彎矩?曲率分析，得到了截面相關曲率延性指標，如表4所示。根據曲率延性指標，采用文獻[16]的方法計算各破壞狀態的曲率延性比()，結果見表5。

表4 拱腳截面延性指標

表5 鋼管混凝土拱肋破壞等級劃分

運用調幅后的地震波，對該鋼管混凝土系桿拱橋進行增量動力分析。本文以拱腳截面曲率作為地震反應指標，并將結果繪制于以ln()為縱坐標、ln()為橫坐標的直角坐標系中，對拱腳處的地震響應進行擬合，得到各級損傷狀態的線性回歸函數，見表6。

表6 各損傷狀態回歸函數參數

得到以上擬合回歸函數后，結合式(3)即可得到不同損傷狀態對應的地震易損性曲線，如圖5所示。

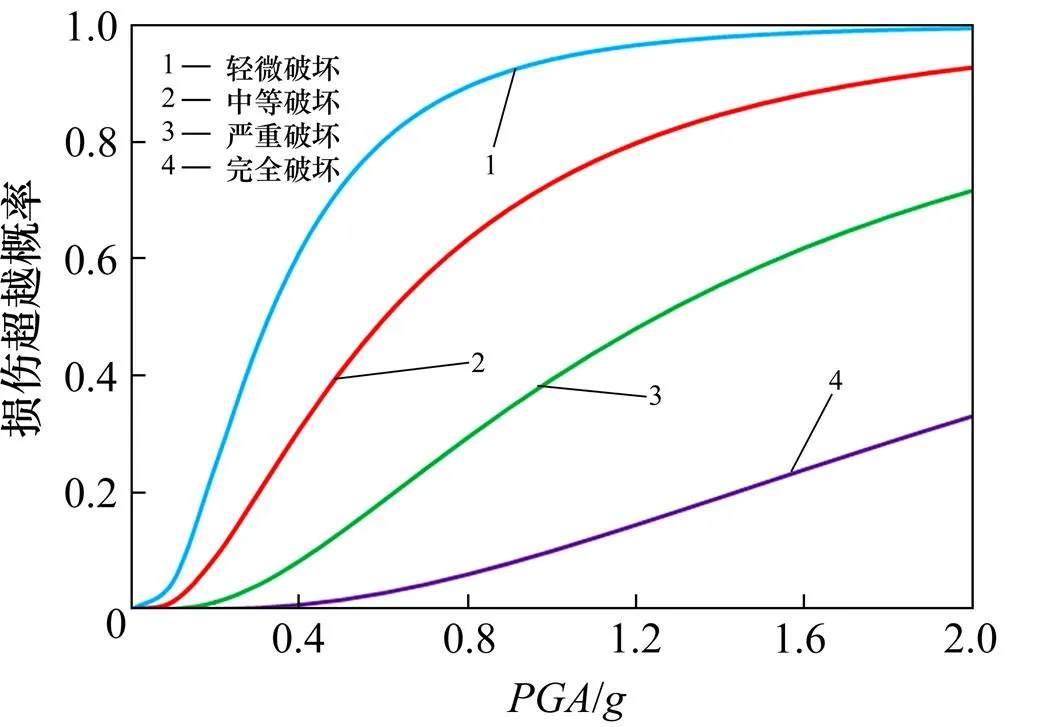
圖5 拱腳地震易損性曲線

由圖5可知，當=0.2，0.4和0.8時，發生輕微破壞的概率分別為25%，61%和89%，發生中等破壞的概率分別為9%，31%和63%，發生嚴重破壞和完全破環的概率均較小。由此表明，該橋總體抗震性能較好，地震作用下具有良好的安全性和可靠性。

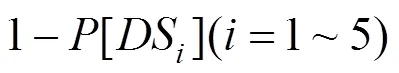
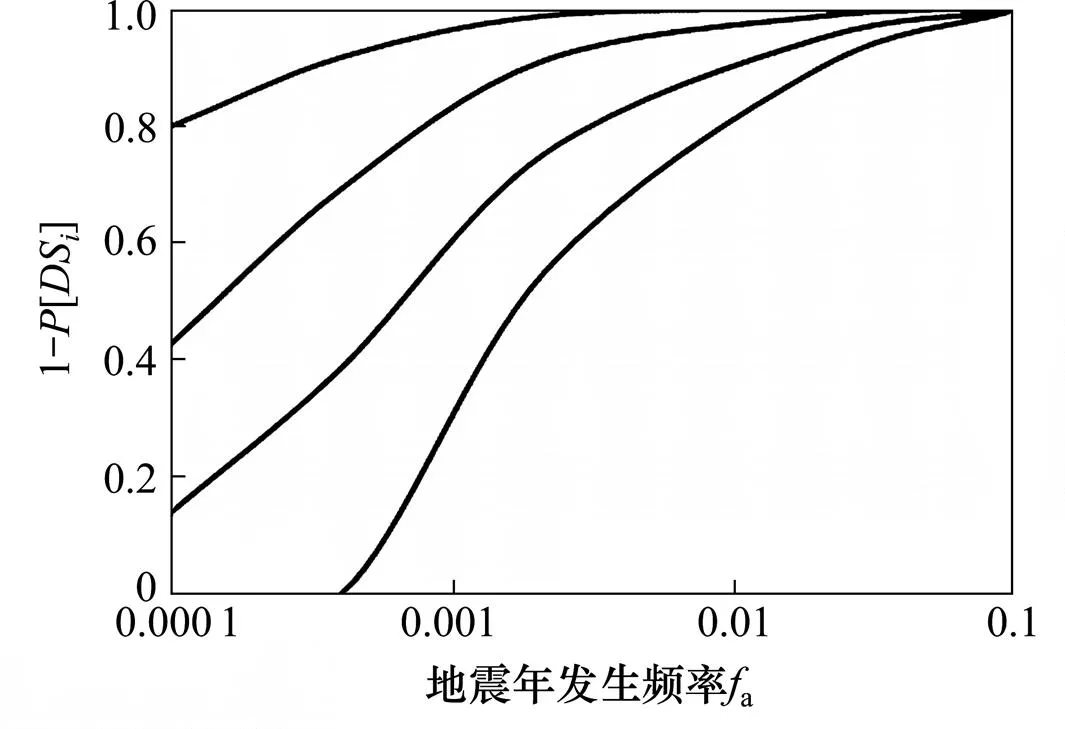
圖6 拱腳存活概率曲線

4.2 地震經濟風險評估

4.2.1 損傷概率分析

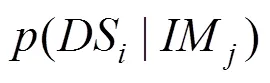
=1時，

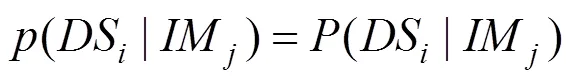
>1時，

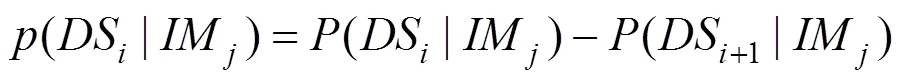
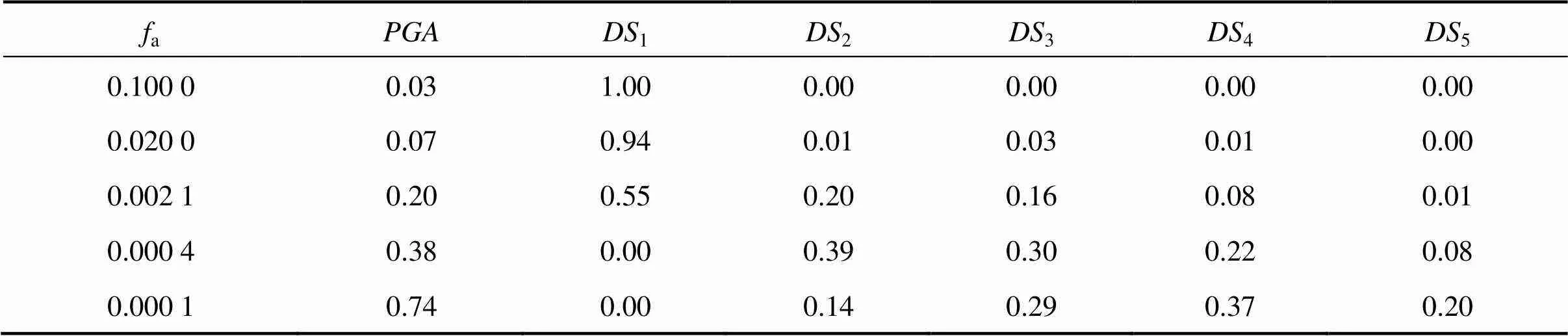
表7 損傷狀態概率

由表7可知，0≤≤0.07時，拱腳位置(1)=1，表明該類地震作用下，拱腳能夠處于完好狀態；當0.07＜≤0.2時，(1)逐漸減小，(2)~(4)不同程度逐漸增大，(5)=0，表明在該類地震作用下，拱腳位置處于完好狀態的概率較大，也可能發生輕微破壞或中等破壞，但嚴重破壞和完全破壞的可能性極小；當0.2＜≤0.38時，(1)瞬減至0，(2)~(5)均不等幅度逐漸增大，表明在該類強度地震作用下，拱腳位置發生輕微、中等和嚴重破壞的概率逐漸增長；當0.38＜≤0.74時，(2)開始減小，(3)基本不變，(4)和(5)增長較快，表明在該強度地震水平下，發生中等和嚴重破壞的概率逐漸超越輕微破壞概率。

4.2.2 經濟損失風險分析

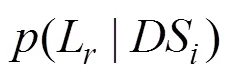
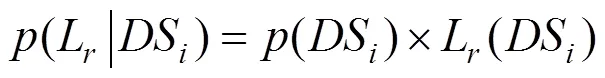
結構在某一超越概率地震作用下的總損失率是5個損傷狀態對應的損失概率之和，根據表8便可繪制出該橋的地震經濟累計風險曲線(見圖7)，該曲線表示結構在某一給定超越概率地震下可能造成的總損失率。

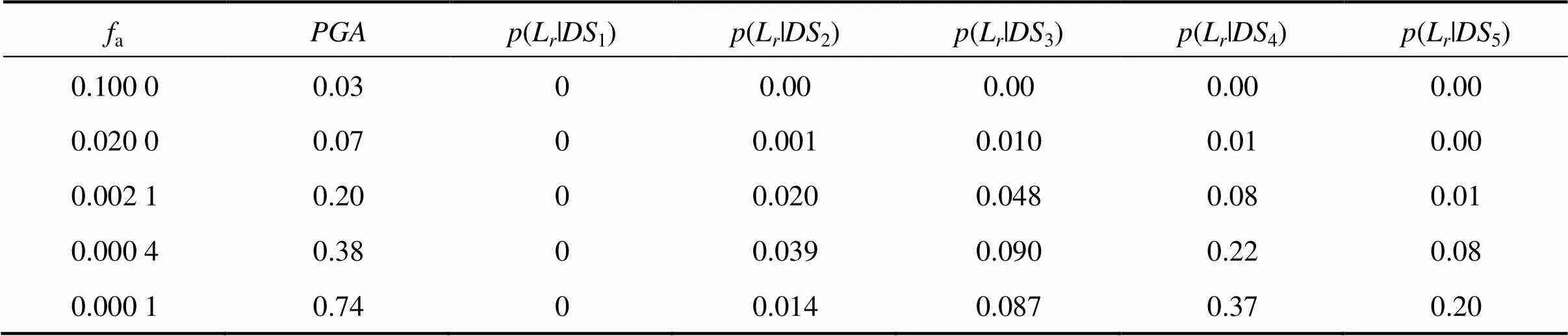
表8 各損傷狀態損失比的條件概率

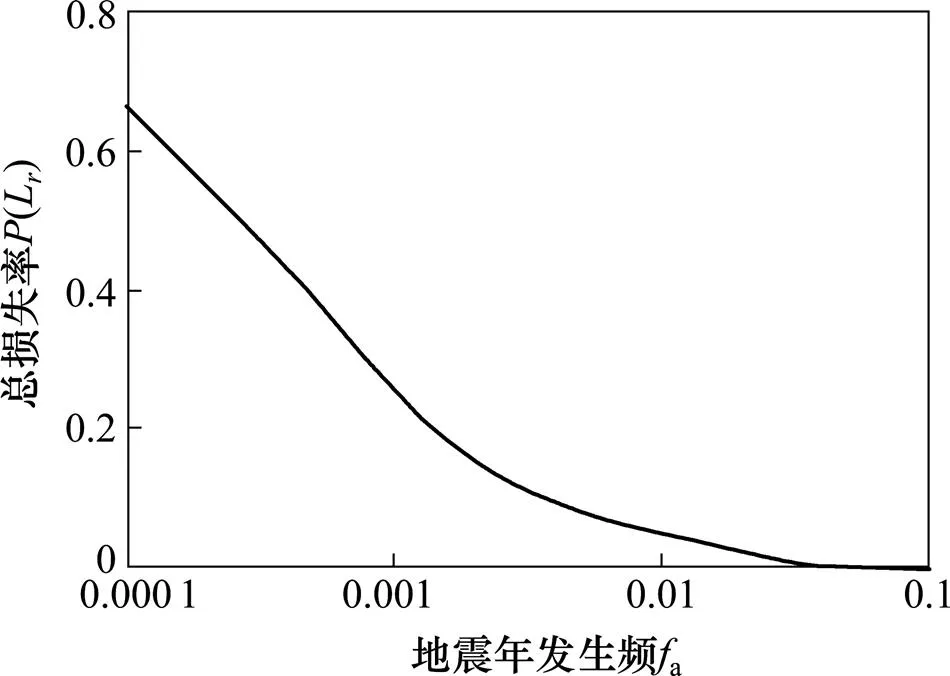
圖7 地震累計風險曲線

根據圖7可得年發生頻率分別為0.1，0.02， 0.002 1，0.000 4和0.000 1的地震作用下的總損失率[L]，再依據式(5)便可計算該拱橋在不同a地震下的每百萬元產值年預期損失。計算結果如表9所示。

綜合以上分析：1) 由圖7可知，累計損失風險隨著地震危險性的降低而減少；2) 由表9可知，該橋經濟損失主要集中于年超越概率為0.02~0.002 1之間的地震，在該類地震作用下，本橋每百萬元產值的累計年預期損失達2 442.05元，占整體損失的77.3%。

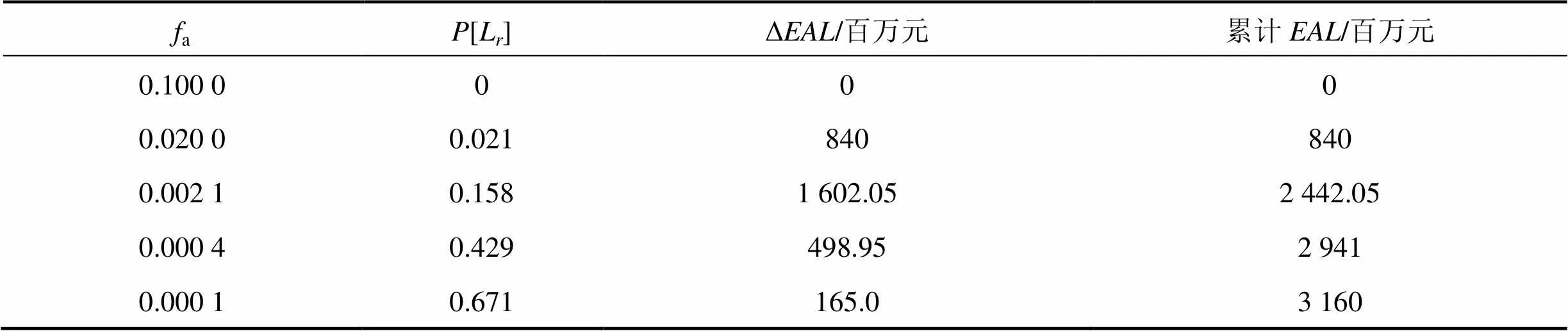
表9 每百萬元產值年預期損失

5 結論

1) IDA分析方法根據給定的工程需求參數，能夠確定結構在不同地震水平和特征下的動力響應，建立結構易損性曲線，可以有效評估橋梁結構在不同年超越概率地震作用下的經濟風險損失。

2) 將橋梁結構抗震性能概率需求特征與年預期損失(EAL)相結合，可全面考察結構的地震直接經濟風險。實例表明：該橋的地震直接經濟損失主要來源于年超越概率為0.02~0.002 1的中小級別地震，占整體損失的77.3%。

3) 基于全概率的評估理論考慮了地震作用和結構非線性行為包含的不確定性，能夠合理地評估橋梁結構的地震經濟風險。同時將地震風險用定量的經濟指標形式來表達，有助于除工程師以外的相關決策者(業主、保險人員等)更好理解其風險，對震后橋梁的加固或新建做出合理決策。

本文僅考慮在確定地震作用下該橋的直接經濟損失，但橋梁作為交通線路重要樞紐，一旦發生破壞，引起的間接損失不容忽視。因此，綜合考慮地震隨機性和橋梁間接損失有助于更全面、更準確地描述該類結構地震經濟風險。

[1] Cornell C A, Krawinkler H. Progress and challenges in seismic performance assessment[J]. Peer Center News, 2000, 20(2): 130?139.

[2] Cornell C A, Jalayer F, Hamburger R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4): 526? 533.

[3] Fajfar P, Krawinkler H. Performance-based seismic design concepts and implementation, PEER report 2004/05[R]. Berkeley: Pacific Earthquake Engineering Research Center, 2004.

[4] 羅文文, 李英民, 韓軍. 基于全概率PBEE方法的RC框架結構地震損失分析[J]. 工程力學, 2016, 33(9): 186?194. LUO Wenwen, LI Yingmin, HAN Jun. Earthquake loss estimation for RC frames based on PEER-PBEE methodology[J]. Engineering Mechanics, 2016, 33(9): 186?194.

[5] 韓建平, 褚小嘉. 基于易損性分析的RC框架?填充墻結構地震直接經濟損失計算[J]. 世界地震工程, 2016, 32(3): 13?20. HAN Jianping, CHU Xiaojia. Seismic direct economic loss analysis of infilled RC frame structrue based on fragility analysis[J]. World Earthquake Engineering, 2016, 32(3): 13?20.

[6] ZHANG K, ZHU X, JIANG Cheng. An application of seismic financial risk assessment of three-span continuous rigid frame bridge[C]// The 14th World Conference on Earthquake Engineering. Beijing, China, 12-17. Oct, 2008.

[7] Moehle J, Deierlein G G. A framework for performance-based earthquake engineering[C]// Proceedings of the 13th World Conference on Earthquake Engineering, 2004.

[8] Dhakal R P, Mander J B. Financial risk assessment methodology for natural hazards[J]. Bulletin of the New Zealand Society for Earthquake Engineering, 2006, 39(2): 91?105.

[9] 趙人達, 高能, 賈毅, 等. 基于IDA的大跨連續梁橋地震易損性分析[J]. 沈陽建筑大學學報(自然科學版), 2017, 33(4): 672?679. ZHAO Renda, GAO Neng, JIA Yi, et al. Seismic vulnerability analysis of long-span continuous beam bridge based on incremental dynamic analysis[J]. Journal of Shenyang Jianzhu University (Natural Science), 2017, 33(4): 672?679.

[10] 朱健. 結構動力學原理與地震易損性分析[M]. 北京:科學出版社, 2013. ZHU Jian. Structural dynamics and analysis of earthquake fragility[M]. Beijing: Science Press, 2013.

[11] 中國地震局. GB/T 18208.4—2005, 地震現場工作第4部分: 災害直接損失評估[S]. 中華人民共和國國家質量監督檢驗檢驗疫總局, 中國國家標準化管理委員會.北京: 中國標準出版社, 2005. China Earthquake Administration.GB/T 18208.4—2005, Post-earthquake field works—Part 4: Assessment of direct loss[S]. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China. Beijing: Standards Press of China, 2005.

[12] GB 50111—2009, 鐵路工程抗震設計規范[S].GB 50111—2009, Code for seismic design of railway engineering[S].

[13] Vamvatsikos D. Incremental dynamic analysis[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(3): 491?514.

[14] 魏標, 楊添涵, 蔣麗忠. 軌道結構建模精細化程度對高速鐵路連續梁橋地震易損性的影響[J]. 工程力學, 2017, 34(11): 1?9. WEI Biao, YANG Tianhan, JIANG Lizhong. The Effects of model refinement of ballastless tracks on the seismic vulnerability of a continuous bridge on a high-speed railway[J]. Engineering Mechanics, 2017, 34(11): 1?9.

[15] Hwang H, LIU Jingbo, Chiu Y H. Seismic fragility analysis of highway bridges[R]. Mid-America Earchquake Center, The University of Memphis: Urbana, 2001.

[16] Hwang H, 劉晶波. 地震作用下鋼筋混凝土橋梁結構易損性分析[J]. 土木工程學報, 2004, 37(6): 47?51. Hwang H, LIU Jingbo. Seismic fragility analysis of reinforced concrete bridges[J]. China Civil Engineering Journal, 2004, 37(6): 47?51.

Performance-based seismic financial risk assessment of a CFST arch bridge over high-speed railway

FENG Li1, FAN Yanyan1, WANG Li1, LI Ziqi1, 2

(1. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. National and Provincial Joint Engineering Laboratory of Road & Bridge Disaster Prevention and Control, Lanzhou Jiaotong University, Lanzhou 730070, China)

Based on the performance-based earthquake engineering assessment theory, a typical CFST tied arch bridge was taken as an example, finite element software was used to build the bridge model, and the seismic vulnerability of the arch rib was analyzed by the incremental dynamic analysis (IDA) method, then the vulnerability curve of the key section was established. The seismic financial risk can be quantitatively expressed in term of expected annual loss (EAL) by integrating seismic hazard and loss ratio. The results show that the IDA method can be used to assess the overall financial risk exposure to earthquake hazard for a CFST tied arch bridge. The expected annual loss (EAL) expression of seismic economic risk shows that the bridge main financial risk from moderate and small earthquakes, accounting for 77.3% of the total. The designer can improve the structure robustness and reduce seismic financial risk of the bridge through the local reinforcement design of vulnerable area.

high-speed railway; tied-arch bridge; incremental dynamic analysis; vulnerability curve; seismic economic risk

10.19713/j.cnki.43?1423/u.2019.03.003

U24；TU398+.9

A

1672 ? 7029(2019)03 ? 0573 ? 08

2018?04?06

長江學者和創新團隊發展計劃滾動支持資助項目(IRT15R29)

樊燕燕(1976?)，女，河南禹州人，副教授，從事橋梁結構健康監測及地震風險評價研究；E?mail：12062481@qq.com

(編輯 涂鵬)