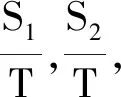一道萬有引力好題

李志強

(華中師范大學第一附屬中學 湖北 武漢 430223)

在萬有引力這一章的所有知識基本學完后，筆者在一堂課上給學生解決練習題中的疑難點，遇到了下面這一道題.

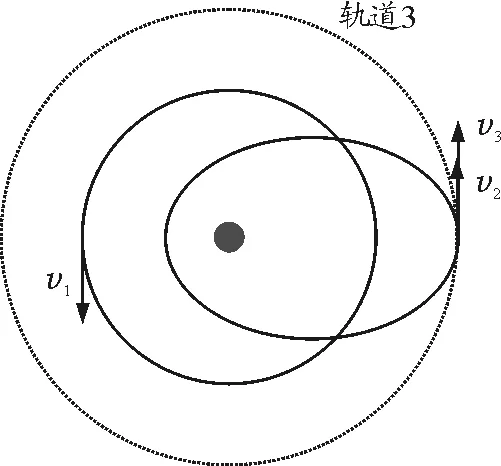
【例題】兩顆人造衛星繞地球逆時針運動,衛星1、衛星2分別沿圓軌道、橢圓軌道運動,圓的半徑與橢圓的半長軸相等,兩軌道相交于A,B兩點,某時刻兩衛星與地球在同一直線上,如圖1所示,下列說法中正確的是( )

A.兩衛星在圖示位置的速度v2=v1

B.兩衛星在A處的加速度大小相等

C.兩顆衛星在A或B點處可能相遇

D.兩衛星永遠不可能相遇

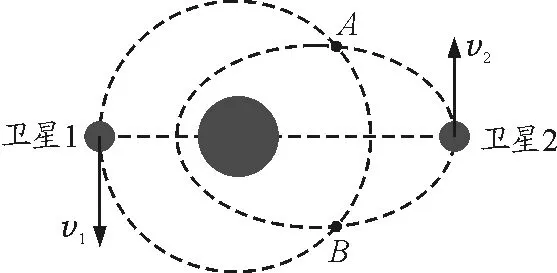
圖1 例題題圖

此題中，選項B，C，D均比較容易判斷.由萬有引力定律和牛頓第二定律可以知道，兩衛星在A點的加速度大小相等.兩顆衛星軌道半長軸相等，中心天體相同，由開普勒第三定律可知，它們周期相等，因此當衛星1位于軌跡下半周時，衛星2位于軌跡上半周，所以它們永遠不會相遇.

但對于選項A的解釋并不是非常容易，筆者在和學生互動時，學生的思維活躍程度令人驚喜，他們給出了以下多種解釋方法.

解法1：

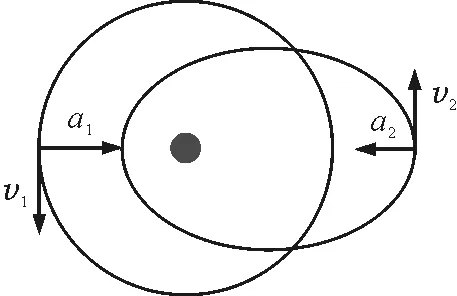
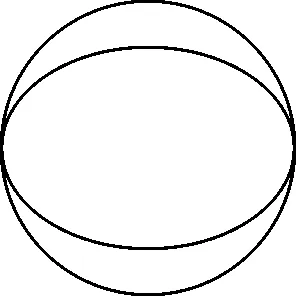
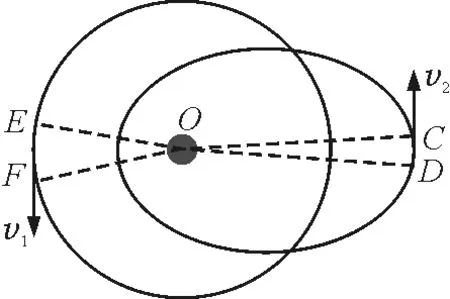
利用衛星變軌的知識.如圖2所示，想象一個與橢圓軌道遠地點相切的圓形軌道，記為軌道3.設衛星在軌道3上運行的速度為v3，根據萬有引力定律和圓周運動規律，我們可以知道v3

圖2 解法1分析示意圖

解法2：

圖3 解法2分析示意圖

解法3：

圖4 解法2分析ρ1>ρ2解法3分析S1>S2

圖5 解法3分析v1>v2

一節普通的習題課，無意間仿佛變成了一節高效的復習課.此題的解法中涉及到開普勒第二、第三定律，萬有引力定律、牛頓第二定律、圓周運動、衛星運動規律等知識，在同學們的講解和分享過程中不知不覺對這些知識都進行了復習.尤其是解法2，對于圓周運動向心加速度表達式的理解要求很高，要能區分曲線某一點的曲率半徑與該點到中心天體球心的距離，這正是很多同學易產生困惑的難點.在這節課上，提出了解法的幾位同學很有成就感，其他同學聽完這3種解法，都嘖嘖稱贊，顯得很興奮.這樣一道好題不但給了學生思考和展示的機會，同時也是對萬有引力定律這一章知識認真細致的復習.因此，我們的單元復習課和高三的復習課，也可以精心挑選和設計一些好題，讓學生在開放的課堂氛圍中思考、討論，從而達到綜合運用知識和復習的目的，比教師“一言堂”或者讓學生做許多重復訓練要好得多.