碳纖維復合材料凹槽缺陷空氣耦合超聲導波檢測

鄒 琪， 王明泉， 楊順民， 張 曼

(中北大學 信息與通信工程學院， 山西 太原 030051)

0 引 言

復合材料是運用先進的材料制備技術將兩種或兩種以上的材料組分優化組合而成的新材料. 它不僅可以保持各組分材料性能的優點， 而且通過各組分性能的互補和關聯可以獲得單一組成材料所不能達到的綜合性能[1-2]. 因此， 復合材料代替了很多傳統材料， 在很多領域發揮著重要作用， 對科技的發展也有著不可替代的作用. 但是， 在生產工藝和使用過程中， 難免會出現一些缺陷損傷， 這也成為復合材料在實際應用中面臨的一大挑戰. 為避免損傷所帶來的不堪設想的后果， 及時檢測獲知健康狀況信息就顯得十分重要[3].

無損檢測方法多種多樣， 也各有利弊. 目前， 傳統的空氣耦合C掃描檢測系統在國內外發展迅速. 空氣耦合C掃描技術適用于穿透法檢測， 將發射和接收探頭分別置于被檢試件兩側并進行逐點掃描， 掃查范圍有限且耗時較長. 而本文采用空氣耦合超聲導波檢測， 將探頭置于被檢材料同側， 可掃查的范圍廣， 又在傳統超聲導波檢測基礎上， 無需使用耦合劑， 以空氣作為耦合方式， 具有檢測效率高、 檢測速度快等特點， 更加便捷快速地定位缺陷[4-7].

1 空氣耦合超聲導波檢測原理及方法

1.1 導波的基本技術

導波是聲波在板、 棒、 管等結構中傳播時， 不斷地與介質的上下邊界發生折射、 反射及縱波與橫波之間的波形轉換作用而產生的波. 導波技術適用于大面積快速檢測， 導波在板狀結構傳播過程中， 產生的板波為Lamb波[8]， 遇到板中的缺陷、 劃槽以及邊界時， 導波信號會發生散射、 反射和透射現象， 正是基于這種現象， 反射回波中含有頻散或轉化的模態， 可以代表材料、 結構或者缺陷的信息[9-10]. 實現導波檢測的關鍵問題是分析復合材料中導波的傳播特性， 選擇合適的模態和探頭的頻率， 通過對回波信號的分析， 快速準確地判斷材料的健康狀況.

1.2 頻散曲線繪制和探頭角度計算

導波在板中傳播過程中會發生很嚴重的頻散現象， 主要與頻厚積有關[11]. 根據板中質點振動的相位關系把導波的模式分為對稱模式和反對稱模式， 對稱模式分為S0，S1，S2，S3， …，Sn等多個模式， 反對稱模式分為A0，A1，A2，A3， …，An等多個模式[12-13].

頻散現象和多模態特性使得導波在傳播中與缺陷的作用顯得十分復雜， 增加了對缺陷定位分析的難度[14]. 因此， 對頻散曲線的分析是研究導波頻散特性， 選擇合理的模態， 確定探頭入射角度的基礎和關鍵. 本文以厚度為2 mm的碳纖維復合材料為研究對象， 材料的性能參數分別為：ρ=1.56 g/cm3，E=13.260 3 GPa，ν=0.483 2， 使用有限元分析法， 采用ABAQUS軟件對導波在復合板的傳播特性進行分析， 繪制圖 1 所示的頻散曲線.

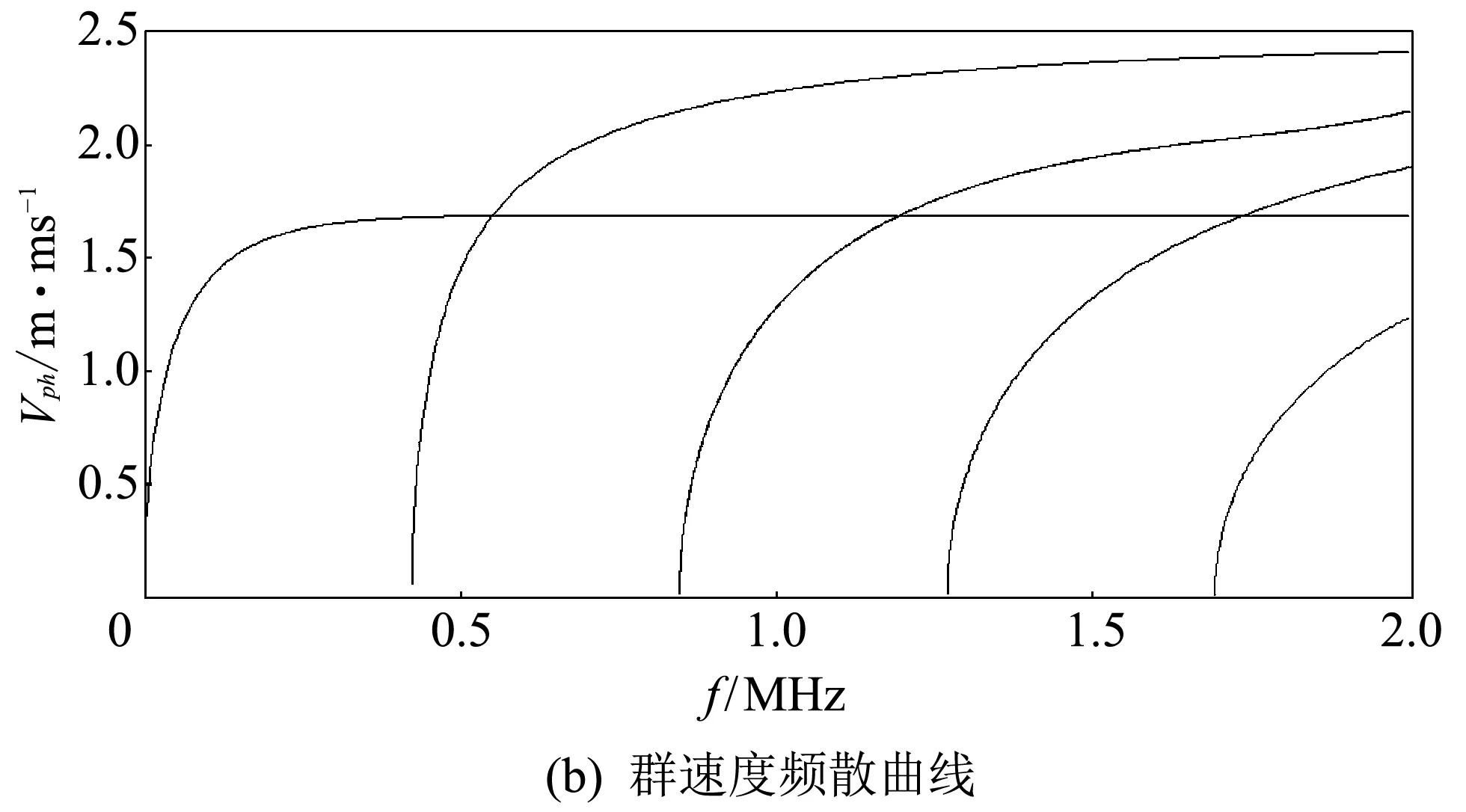
圖 1 頻散曲線Fig.1 Dispersion curve

分析圖 1 的頻散曲線可知， 每個模態都存在頻散現象， 群速度和相速度都會隨著頻率的變化而變化， 不同模態的導波頻散程度有很大差別， 而同一模態的導波在不同的頻率范圍內也會有不同的頻散程度； 在同一頻率下， 會產生2個或2個以上的導波模態， 每個模態都會有各自的群速度和相速度. 而頻率越高， 激勵的模態越多， 因此， 挑選合適的模態作為目標模態就尤為重要了. 通過分析頻散曲線可知應選擇較低的激發頻率， 因為頻率在0～0.4 MHz之間只存在一種A0模態， 低于其它模態的截止頻率， 簡化了板中聲場情況， 一般情況下， 不會發生模態間的干擾和轉化. 本文選取A0模態作為目標模態進行提取分析， 選取中心頻率為0.2 MHz的空氣耦合平探頭進行綜合分析. 分析相速度頻散曲線中對應頻率為0.2 MHz下的A0模態. 根據Snell[15]定理可得

(1)

式中：θ0為探頭的入射角；θ1為入射聲波傳播進入板材后與法線的夾角；c0為超聲波在空氣中的傳播速度，c0=340 m·s-1；c1為A0模態在 0.2 MHz 下在板中傳播的相速度，c1=1 088 m·s-1. 代入相應數據即可求得θ0， 反射角等于入射角， 即探頭的入射角θ0=18.208 6°.

2 實驗結果分析

2.1 試件的準備

選取厚度為2 mm碳纖維復合材料板作為實驗試件， 在其表面制作人工模擬劃槽缺陷. 為研究在深度一定的情況下， 不同寬度對導波信號的影響狀況， 制備了深度為0.5 mm， 寬度分別為 1 mm， 2 mm， 3 mm的3種人工模擬劃槽.

2.2 實驗結果及分析

如圖 2 所示實驗采用頻率為0.2 MHz的平探頭， 壓電晶片大小為20 mm×14 mm， 將一發一收探頭同側對向放置， 發射探頭和接收探頭中心間距為18 mm， 根據前文中計算出的入射角度對兩個探頭進行角度調整. 首先將準備好的完好無缺陷的碳纖維復合板置于探頭下側， 探頭與板間距調整5 mm， 得到如圖 3 所示的接收信號； 第2步， 將制備好的深度為0.5 mm， 寬度為1 mm的人工模擬劃槽缺陷置于兩探頭之間， 得到如圖 4 所示的導波接收信號； 第3步， 分別將制備好的2 mm和 3 mm 人工模擬劃槽缺陷置于探頭之間， 得到圖 6 和圖 7 所示的接收信號. 為了減少測量誤差， 使實驗數據更具可靠性， 此次實驗分別對4種狀況下的碳纖維復合板采10組數據， 每組數據包含3 000個采樣點， 采樣點的橫坐標代表采樣時間， 采樣頻率為2 MHz； 縱坐標代表幅值， 在Matlab中繪制出波形信號進行對比分析. 表 1 對無缺陷、 1 mm劃槽、 2 mm劃槽和3 mm劃槽情況下采集10組數據的幅值最大值進行統計， 并求取平均值， 目的是為了平均降噪.

圖 2 同側對向探頭實驗現場Fig.2 Same side opposite probe test site

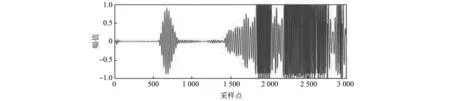
圖 3 無缺陷情況接收信號Fig.3 Receive signal without defect

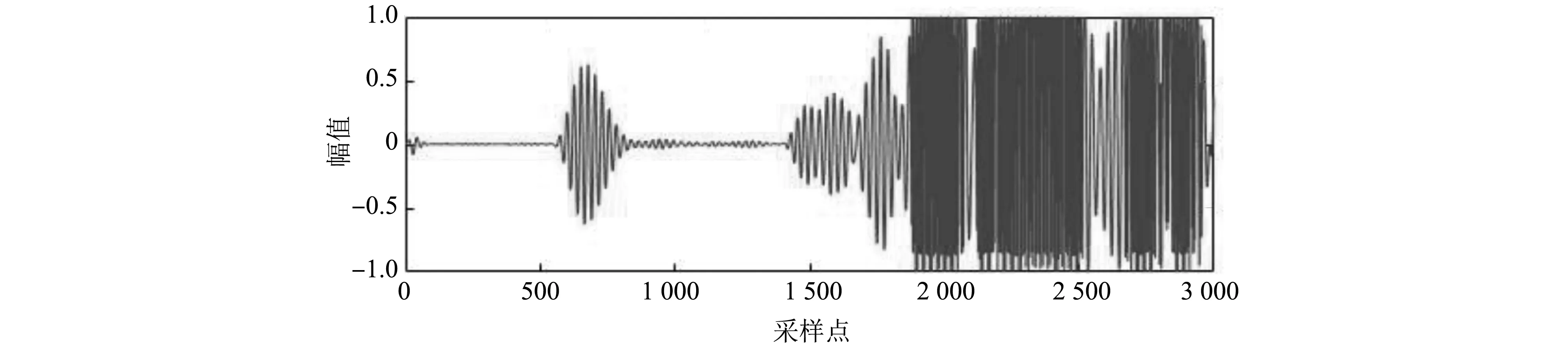
圖 4 劃槽1 mm時接收信號Fig.4 Receive signal when slotted 1 mm

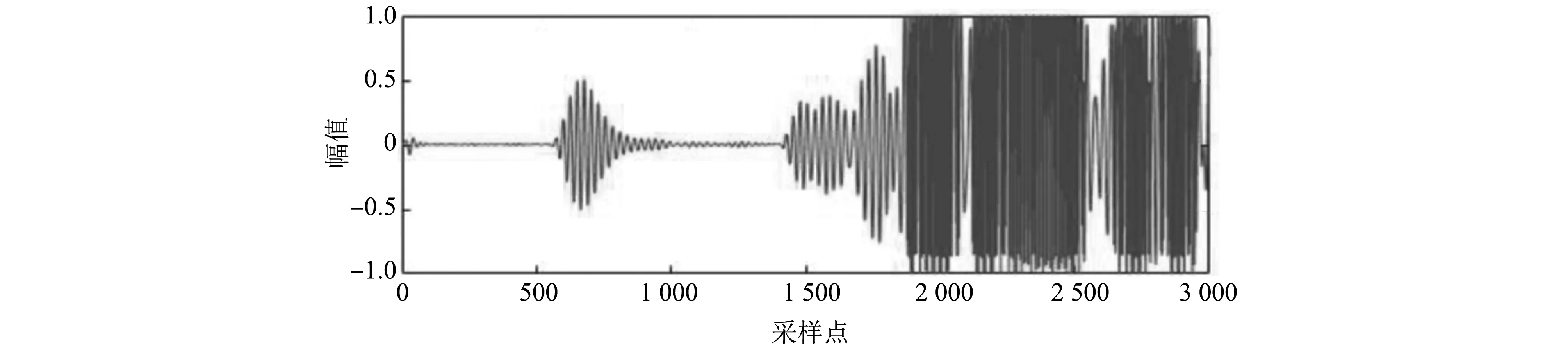
圖 5 劃槽2 mm時接收信號Fig.5 Receive signal when slotted 2 mm

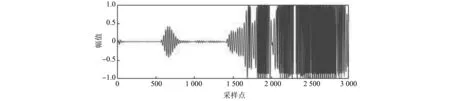
圖 6 劃槽3 mm時接收信號Fig.6 Receive signal when slotted 3 mm

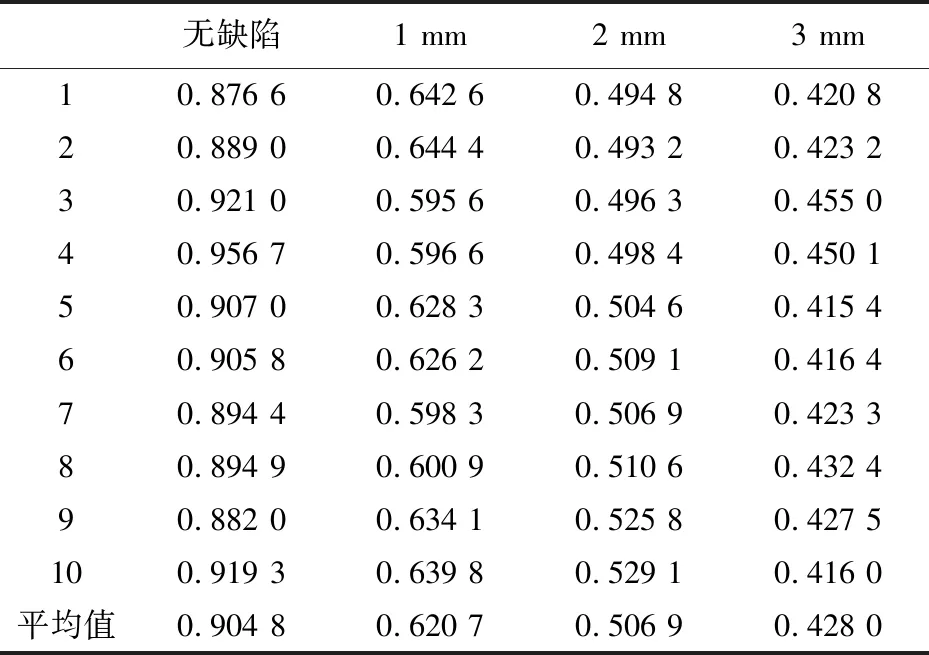
無缺陷1 mm2 mm3 mm10.876 60.642 60.494 80.420 820.889 00.644 40.493 20.423 230.921 00.595 60.496 30.455 040.956 70.596 60.498 40.450 150.907 00.628 30.504 60.415 460.905 80.626 20.509 10.416 470.894 40.598 30.506 90.423 380.894 90.600 90.510 60.432 490.882 00.634 10.525 80.427 5100.919 30.639 80.529 10.416 0平均值0.904 80.620 70.506 90.428 0

由表 1 可以看出： 當碳纖維復合板出現劃槽缺陷時， 導波信號的最高幅值呈現衰減狀態， 且隨著劃槽寬度的增加， 導波信號的最高幅值始終呈衰減趨勢. 無缺陷的碳纖維復合板最高幅值的平均值是0.904 8； 表面有1 mm劃槽時最高幅值平均值是0.620 7， 相比無缺陷的最高幅值衰減了0.284 1； 表面有2 mm劃槽時最高幅值平均值是0.506 9， 相比表面有1 mm劃槽時最高幅值衰減了0.113 8； 表面有3 mm劃槽時最高幅值平均值是0.428 0， 相比表面有2 mm劃槽時最高幅值衰減了0.078 9.

根據計算得出的4種情況下最高幅值平均值， 采用最小二乘法繪制導波信號最高幅值隨劃槽寬度變化的曲線如圖 7 所示. 分析可知： 劃槽缺陷深度一定時， 隨著劃槽寬度的增加， 導波信號最高幅值呈現衰減趨勢， 且衰減的速度越來越慢. 可以初步推斷， 當碳纖維復合板表面出現劃槽時， 導波信號最高幅值會呈現衰減， 并且隨著劃槽寬度的增大， 最高幅值衰減趨于平緩， 呈現出一直趨于零但始終不為零的狀態.

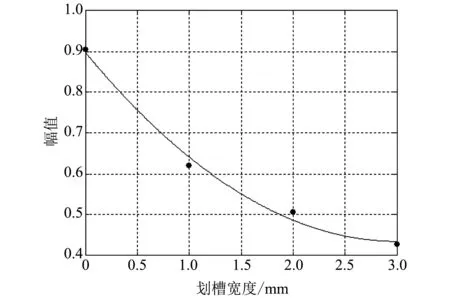
圖 7 劃槽寬度與幅值的關系曲線Fig.7 Shows the relationship between the groove width and the amplitude

3 結 論

傳統的超聲檢測無法實現對有些不能使用耦合劑的特殊材料的檢測， 而耦合劑的使用也使得檢測環境受到限制， 這樣降低了缺陷的檢測精度和效率. 本文采用非接觸式空氣耦合超聲檢測， 無需使用耦合劑， 以碳纖維復合材料為實驗研究試件， 使用0.2 MHz的平探頭同側對向放置法進行檢測， 在深度一定情況下的3種不同寬度劃槽均可被檢出和區分， 檢測方式便捷， 靈敏度好， 效率高， 為空氣耦合超聲導波對碳纖維復合材料的檢測提供實驗依據.